2. 哈尔滨理工大学 机械动力工程学院, 哈尔滨 150080
2. State Key Laboratory of Robotics and System(Harbin Institute Technology), Harbin 150080, China
由于人体个体差异,人体股骨的形状、大小都不相同,尤其是骨骼先天性畸形的人群,标准化假体已经不能满足各类人群对假体置换的要求,已有医学临床经验证明股骨假体使用寿命关键是要看股骨假体柄的形状是否与股骨上段髓腔形态结构达到良好的匹配,因为良好的匹配可以减少应力集中,从而达到长期使用的效果 [1]. 同时,也有学者质疑人体的股骨头形状并不是球体,而是蚶线绕中心轴旋转而成的蚶线球体[2]. Afoke等[3]通过研究发现,人体股骨头确实与标准球体有些偏差. 对此国内的一些专家也开始研究,丁秀敏等[4]对半球与椭球形状人工股骨头对髋臼应力分布进行对比分析,得出结论是椭球形人工股骨头的应力分布更均匀. 目前,常用的股骨假体材料有金属材料、生物陶瓷和复合材料3种,它们有各自不同的特点和临床效果[5].
综上所述,大部分研究是依据不同结构或不同材料假体模型的有限元分析结果,得到假体载荷、变形量等单项指标评价情况.目前还没有将多目标评价方法应用于股骨假体优选研究. 假体与人体组织的相容性和假体的稳定性都是由多种因素决定的,这些因素会对每一个评价指标产生复杂的影响,单目标的假体优选不能给患者提供最好的选择.
本文提出将股骨头与定制的假体柄分体设计并进行股骨假体结构优化,提出多目标优化方法优选材料匹配方案,利用有限元方法实现力学分析,利用模糊物元法实现股骨假体多目标优选,并基于以上思想确定出股骨假体优选流程,改善了依据单一目标进行股骨假体优选的研究现状.
1 股骨及假体结构建模 1.1 股骨内外轮廓线的提取利用医学专用软件MIMICS导入多张DICOM格式的文件图像,本研究共导入461张CT图像,通过阀值设定、面罩编辑、区域增长、3D计算、光顺处理和网格划分等步骤,最终得到股骨的内外轮廓线.
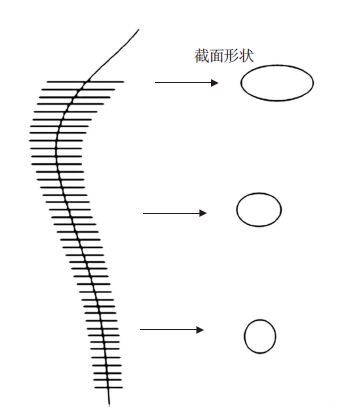
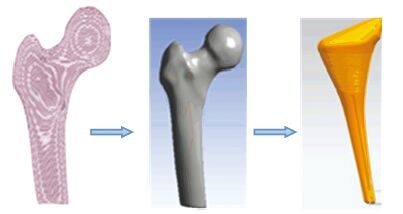
1.2 股骨假体柄结构设计将MIMICS中提取的轮廓线导入UG中,然后分别对假体柄和球头进行建模. 对假体柄进行建模时采用中心线多截面混合法,如图 1所示. 图 2是混合扫描后得到的假体柄,股骨假体柄模型在干骺端进行横条纹处理,以增大假体与股骨的摩擦,增加假体的固定度,防止假体松动. 在股骨干部分进行竖条纹处理,目的是防止假体转动,进而防止假体松动和微动.
|
图 1 中心线及特定位置的截面形状 |
|
图 2 提取股骨轮廓线实现三维重建 |
人工关节假体的稳定性另一影响因素为假体球头与髋臼的匹配状况. 建立3种不同形状的股骨头,优化股骨头和髋臼的匹配形式. 球状人工股骨头的直径为26 mm,根据球状股骨头的尺寸,椭球股骨头尺寸的长轴取为26 mm,短轴为24 mm;蚶线球体股骨头的尺寸是根据Wenschik计算的,蚶线球体由蚶线绕中轴线旋转而成,蚶线在柱坐标系下的几何公式为r=a+bcos Φ,其中a=12.258,b=14.235[6]. 3种形状股骨头在人体矢状面内投影均是圆形,在冠状面、横断面内分别是圆、椭圆和蚶线.
1.4 股骨模型与假体模型的装配根据提取外轮廓线建立股骨模型,模型建好后,将股骨三维实体导入UG中,在UG中对股骨模型进行处理,完成股骨模型与假体模型的装配.
2 股骨假体材料性能对比选择材料的原则为:首先在假体研制方面应尽量保证假体建模精度以及加工精度,避免出现应力集中现象;在材料选择方面说应该尽量优选出生物相容性好、抗磨性高的假体材料. 本研究依据文献选取锆铌合金、氧化锆陶瓷、碳纤维增强的聚醚酮复合材料3种材料[7],通过3种材料的组合,利用多目标优化手段优选出材料设计模型.
3 有限元模型的建立将建好的模型导入ANSYS中,对球头与髋臼模型采用8节点4面体单元分别进行网格划分,球形球头与髋臼模型共划分为11 046个单元,椭球形球头与髋臼接触模型共划分为12 428个单元,蚶线球形球头与髋臼接触模型共划分为10 033个单元. 将球头与髋臼之间的接触方式定义为面-面接触,根据接触准则可知,如果在面-面接触的两种材料中,一种材料的刚度大于另外一种材料,则应设定刚度较大的材料所在的面为标准面. 由材料学知识可知锆铌合金刚度大于髋臼,因此,在此处接触设置时以球面为标准面,髋臼为接触面. 接触方式为“标准接触”,摩擦系数u取0.1[8].
3.1 材料参数的设置和材料匹配方式经性能优选,选出3种假体材料,分别为锆铌合金、氧化锆陶瓷、碳纤维增强的聚醚酮复合材料,3种材料及股骨的性能参数[9]见表 1.
| 表 1 材料性能 |
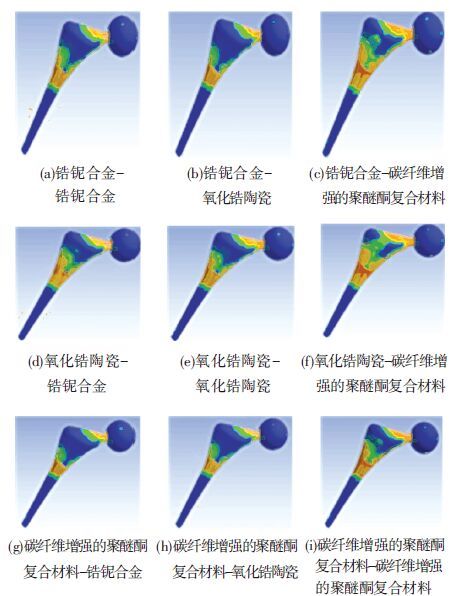
对球头及假体柄分别进行材料优选,进而获取最优材料组合. 根据3种材料参数,分别对球头与假体柄进行赋材,其中包括:(A)锆铌合金-锆铌合金,(B)锆铌合金-氧化锆陶瓷,(C)锆铌合金-碳纤维增强的聚醚酮复合材料,(D)氧化锆陶瓷-锆铌合金,(E)氧化锆陶瓷-氧化锆陶瓷,(F)氧化锆陶瓷-碳纤维增强的聚醚酮复合材料,(G)碳纤维增强的聚醚酮复合材料-锆铌合金,(H)碳纤维增强的聚醚酮复合材料-氧化锆陶瓷,(I)碳纤维增强的聚醚酮复合材料-碳纤维增强的聚醚酮复合材料.
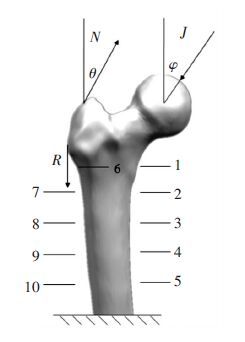
3.2 载荷的构建由于股骨载荷多变且方向不定,计算比较复杂,现将股骨受力进行简化,如图 3所示. 状态1为静态受力,假设人体是单脚站立的负重状态;状态2为动态受力,假设人体是匀速行走状态[10]. 状态1中髋臼对股骨的作用力J为1 588 N,臀肌肌群力N为1 039 N,骼肌束肌力R为169 N. 状态2中的载荷为交变载荷,股骨在人体平面上的载荷范围[11]J为684~1 588,N为586~1 039 N,R为0. 状态2中的载荷状态将在疲劳分析中加以考虑.
|
1~5内测点,6~10外测点 图 3 股骨Y方向受力简图及测点分布 |
1) 股骨假体额定载荷. 股骨假体在不发生破损下的最大载荷可以评价假体的承载性能:
| ${{\sigma }_{i}}\left( F \right)<P{{\sigma }_{\text{bi}}}.$ |
式中: σi(F)为作用在股骨假体上的最大载荷应力值,σbi为股骨假体屈服强度,P为安全系数.
2) 股骨假体疲劳寿命. 变幅应力下寿命计算公式如下:
| $N=\gamma \sum\limits_{i-1}^{n}{ni}=\omega \sum\limits_{n-1}^{n}{{{n}_{i}}}/\sum\limits_{n-1}^{n}{{{n}_{i}}}/{{N}_{i}}.$ |
式中:λ为零件可以承受的载荷循环总周期数,ω值为0.68,ni为零件每次运行中的某一种循环的次数,Ni为该循环的疲劳极限.
3) 股骨假体应力遮挡率. 在股骨的某一点的应力遮挡程度通常用应力遮挡率η表示,计算某一点应力遮挡率公式:
| $\eta =\left( 1-\sigma /{{\sigma }_{0}} \right)\times 100%.$ |
式中:σ0为假体未置换前股骨所承受的正常应力,σ为假体置换后同一点股骨所承受的应力.
4) 股骨假体最大变形量. 股骨模型设置为弹性模型,由广义胡克定律形式的弹性变形方程计算股骨假体变形量.
4.2 股骨假体优选方法由于评价股骨假体性能指标的多样化,不能以单一指标来衡量一个股骨假体的好坏,且各指标之间存在一定的模糊性和不相容性,故本研究采用模糊物元分析法实现股骨假体的多目标优化.
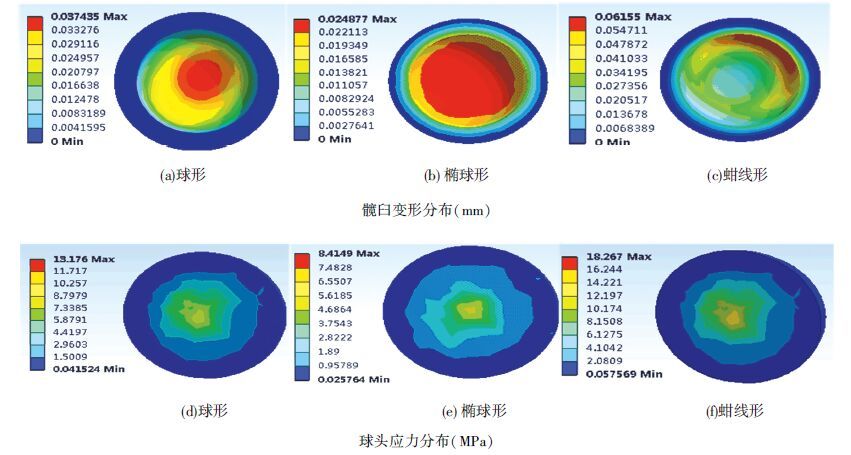
5 仿真分析及结果 5.1 优选球头结构的力学仿真以锆铌合金为股骨假体材料,分别对球形球头、椭球形球头、蚶线球形球头进行力学仿真. 图 4(a)、(b)、(c)是髋臼模型分别与3种不同形状股骨头匹配时其变形分布. 球形股骨头作用在髋臼模型上时,髋臼最大变形量发生在中心处,且随着半径的增大变形量减小,最大变形量为0.037 mm;椭球形股骨头作用在髋臼模型上时,最大变形量也发生在球心处,最大变形量为0.025 mm;而蚶线球形股骨头则不同,其对髋臼模型产生的最大变形量位置发生在偏离球心处,说明蚶线形股骨头与髋臼没有直接接触. 最大变形为0.062 mm. 图 4(d)、(e)、(f)显示相同载荷条件下3种球头的应力分布云图. 3种形状球头的最大应力均出现在中心位置,且以中心为半径,随着半径的增大应力值逐渐减小,球形股骨头最大应力为10.25 MPa,椭球形股骨头的最大应力为5.39 MPa,蚶线球体股骨头的最大应力值为12.19 MPa. 对3种球头表面进行取点测量可知,球形股骨头表面应力在0.041~1.500 MPa,椭球形股骨头的表面应力为0.025~0.920 MPa,蚶线球形球头的表面应力为0.057~2.040 MPa. 椭球形股骨头的中心的内外应力均比相同载荷条件下的其他两种球头值要小.
|
图 4 髋臼变形分布云图和球头应力分布云图 |
由分析可知,3种球头结构中以椭球结构为最优,因此可以确定股骨假体最终结构为椭球形球头+假体柄. 设定球头-假体柄9种材料匹配模型(A)~(I),进行有限元仿真,按照图 3所示测点提取结果绘制趋势图,如图 5所示.
|
图 5 假体置换后股骨测点-应力趋势图 |
由以上分析结果可知,由于A、D、G假体柄材料、结构完全相同,因此应力仿真结果一致,同理可知B、E、H仿真结果相同,C、F、I仿真结果相同. 根据应力遮挡率计算公式可以得出3种假体柄材料的应力遮挡率. 根据以上分析可以得出,C、F、I模型假体柄所用的碳纤维增强的聚醚酮复合材料在载荷作用下对股骨产生的应力遮挡最小,B、E、H 模型假体柄所用的氧化锆陶瓷材料在载荷作用下对股骨产生的应力遮挡最大,进而对股骨的损坏也最大.
同理,分别对以上9种材料匹配方案进行有限元应力仿真,结果如图 6所示.
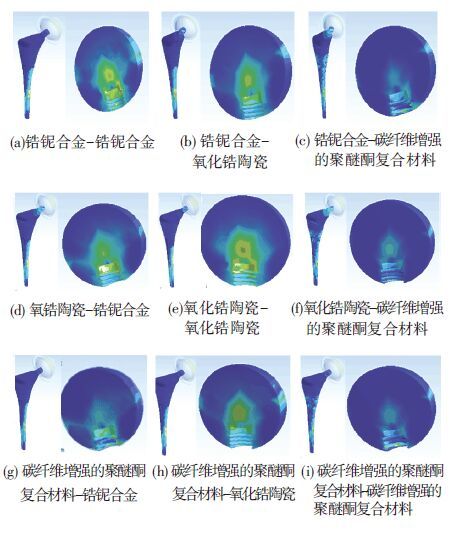
|
图 6 假体ANSYS仿真应力云图 |
图 6为(A)~(I)9种材料匹配方案中假体柄及球头仿真应力分布云图,由仿真结果可知,9种假体均无明显应力集中现象. 但从股骨假体应力分布云图中可以看出,假体易发生应力集中的区域是股骨头与假体柄接触区域,而当假体柄材料为碳纤维增强的聚醚酮复合材料时,假体柄螺纹处应力集中现象相对其他材料明显,因此可以得出复合材料不适合作为股骨假体柄材料,但由应力遮挡率角度来分析得出的结论恰恰与此矛盾,因此需要引入疲劳寿命等指标做进一步分析为股骨假体优选做出判断.
5.3 股骨假体变形分析除假体应力分析外,其变形也是评价假体性能的一个重要指标,提取股骨假体仿真变形分布云图,提取结果如图 7所示.

|
图 7 股骨假体ANSYS仿真变形云图(mm) |
由图 7可知,选用不同材料的球头对股骨假体的变形有很大的影响,例如选用氧化锆陶瓷做球头,假体的变形量是所有模型中最大的. 而选用碳纤维增强的聚醚酮复合材料做球头,假体的变形量相对比较小,模型(G)碳纤维增强的聚醚酮复合材料-锆铌合金股骨头变形分布均匀,且变形量是所有模型中最小的. 通过股骨假体变形分析,球头最适用的材料为碳纤维增强的聚醚酮复合材料,最适用做假体柄的材料为锆铌合金.
5.4 股骨假体疲劳寿命分析疲劳寿命分析结果中寿命分布图见图 8,安全系数分布图见图 9.
通过对股骨假体进行疲劳寿命分析,提取其寿命分析结果,可得出相同载荷条件下不同材料组合股骨假体模型的先后发生疲劳破损的一般顺序,疲劳寿命值从大到小依次为:模型G、模型H、模型B、模型A、模型E、模型D、模型I、模型C、模型F. 分析其原因是材料属性造成它们的疲劳寿命的巨大差异. 提取疲劳寿命分析结果中的安全因子分布图,发现模型I、模型C、模型F的疲劳破损处安全因子更密集,由此也可推断出受力更集中,因此,相同载荷条件下螺纹处更易发生疲劳破坏.

|
图 8 寿命分布 |
|
图 9 安全系数分布 |
1) 股骨假体额定载荷Nσbi. 由于股骨假体由两种材料匹配而成,因此当对两种材料组成的假体进行额定载荷计算时,应以两种材料中屈服强度较低的材料为准进行计算. 安全系数N常用取值为0.2. 根据表 2中的屈服强度值可算出9种假体额定载荷.
| 表 2 各种材料匹配方案额定载荷 |
2) 应力遮挡率根据. 9种股骨假体内外两侧应力平均值提取可以得出9种假体应力遮挡率,如表 3所示.
| 表 3 各种材料匹配方案应力遮挡率 |
3) 最大变形量. 根据股骨假体变形仿真结果可以提取出仿真结果中假体最大变形量,结果如表 4所示.
| 表 4 假体仿真变形最大值统计 |
4) 疲劳寿命. 由疲劳分析仿真结果可知,9种假体疲劳寿命值均大于3.24*107,因此(A)-(I)9种材料匹配方案均可作为股骨假体优选中的备选方案来进行优化,疲劳分析结果如表 5所示.
| 表 5 各种材料匹配方案疲劳寿命 |
对4个特征进行赋值后,采用模糊物元分析方法建立9个实验方案4种优化指标的股骨假体性能综合评价模型:
| $R=\left[ \begin{array}{*{35}{l}} {{x}_{11}} & {{x}_{12}} & {{x}_{13}} & \cdot \cdot \cdot & {{x}_{19}} \\ {{x}_{21}} & {{x}_{22}} & {{x}_{23}} & \cdot \cdot \cdot & {{x}_{29}} \\ {{x}_{31}} & {{x}_{32}} & {{x}_{33}} & \cdot \cdot \cdot & {{x}_{39}} \\ {{x}_{41}} & {{x}_{32}} & {{x}_{43}} & \cdot \cdot \cdot & {{x}_{49}} \\ \end{array} \right]$ | (1) |
式中:x11~x19为股骨假体额定载荷评价指标值,x21~x29为股骨假体应力遮挡率评价指标值,x31~x39为股骨假体最大变形量评价指标值,x41~x49为股骨假体疲劳寿命评价指标值.
应力遮挡率和最大变形量评价指标的从优隶属度为额定载荷和疲劳寿命评价指标的从优隶属度.
| ${{\mu }_{ij}}={{x}_{ij\min }}/{{x}_{ij}},\left( i=1,2,3,4;j=1,2,3,...,9 \right),$ | (2) |
| ${{\mu }_{ij}}={{x}_{ij}}/{{x}_{ij\operatorname{mix}}},\left( i=1,2,3,4;j=1,2,3,...,9 \right),$ | (3) |
| ${{\mu }_{ij}}={{\xi }_{ij}}.$ | (4) |
式中:μij为各评价指标隶属度,ξij为各评价指标关联系数.
关联系数矩阵为
| $R=\left[ \begin{array}{*{35}{l}} {{\xi }_{11}} & {{\xi }_{12}} & {{\xi }_{13}} & \cdot \cdot \cdot & {{\xi }_{19}} \\ {{\xi }_{21}} & {{\xi }_{22}} & {{\xi }_{23}} & \cdot \cdot \cdot & {{\xi }_{29}} \\ {{\xi }_{31}} & {{\xi }_{32}} & {{\xi }_{33}} & \cdot \cdot \cdot & {{\xi }_{39}} \\ {{\xi }_{41}} & {{\xi }_{32}} & {{\xi }_{43}} & \cdot \cdot \cdot & {{\xi }_{49}} \\ \end{array} \right]$ | (5) |
各特征的权重值以及建立评价指标权重矩阵为
| $\sum\limits_{i=1}^{4}{{{\theta }_{i}}=1,}$ | (6) |
| $\text{{W}'}_{i}^{{}}=\sum\limits_{i=1}^{4}{{{\xi }_{ij}}}/\left( \sum\limits_{i=1}^{4}{{}}\sum\limits_{j=1}^{9}{{{\xi }_{ij}}} \right),$ | (7) |
| ${{W}_{i}}={{\theta }_{i}}\text{{W}'}_{i}^{{}}/\left( \sum\limits_{i=1}^{4}{{{\theta }_{i}}\text{{W}'}} \right),$ | (8) |
| ${{R}_{W}}=\left[ {{W}_{1}}\text{ }{{W}_{2}}\text{ }{{W}_{3}}\text{ }{{W}_{4}} \right].$ | (9) |
式中:θi为主观权重,Wi′为客观权重.
由式(5) 与式(9) 采用M(·,+)算子,获取股骨假体复合模糊物元为
| $\begin{align} & {{R}_{k}}= \\ & \left[ {{K}_{1}}=\sum\limits_{j=1}^{4}{{{W}_{j}}{{\xi }_{1j}}\text{ }{{K}_{2}}}=\sum\limits_{j=1}^{4}{{{W}_{j}}{{\xi }_{2j}}\text{ }...{{K}_{9}}}=\sum\limits_{j=1}^{4}{{{W}_{j}}{{\xi }_{9j}}} \right]. \\ \end{align}$ | (10) |
根据以上仿真结果对比分析,可知分析实例中更侧重于疲劳寿命和应力遮挡率两项指标,因此,取主观权重值θ1=0.10,θ2=0.30,θ3=0.20,θ4=0.40,由式(1) ~(10) ,带入4个评价指标特征值,即可获得股骨假体模糊物元为
| ${{R}_{k}}=\left[ 0.6927\text{ }0.7454\text{ }0.4336\text{ }0.5104\text{ }0.6681\text{ }0.5807\text{ }0.8478\text{ }0.7023\text{ }0.5875 \right]$ |
根据以上分析结果可以得出,(A)~(I)9种材料匹配方案中,G方案——碳纤维增强的聚醚酮复合材料-锆铌合金材料匹配方案为最佳方案.
6 结论1) 依据专门患者CT体数据集得出了椭球形球头组合定制式假体柄的最优结构设计.
2) 依据专门患者假体置换环境得出了碳纤维增强的聚醚酮复合材料球头-锆铌合金材料假体柄为最佳材料匹配方案.
| [1] |
赵光明. 人工全髋关节置换三维有限元建模及其在体生物力学研究[D]. 洛阳:河南科技大学, 2013.
( 0) 0)
|
| [2] |
李宏斌, 朱振安. 定制型人工髋关节的临床应用[J].
国外医学骨科学分册,2002, 23 (3) : 161-165.
( 0) 0)
|
| [3] |
AFOKE N Y, BYERS P D, HUTTON W C. The incongruous hip joint a casting study[J].
Journa1 of Bone and Joint Surgery,1980, 62 (4) : 511-514.
( 0) 0)
|
| [4] |
丁秀敏, 侯丽丽, 郭子学. 半球与椭球髋臼假体对骨性髋臼应力分布的对比分析[J].
医用生物力学,2008, 23 (6) : 465-471.
( 0) 0)
|
| [5] |
姚进. 不同材料髋关节假体在髋关节置换中的应用[J].
中国组织工程研究与临床康复,2011, 15 (7) : 3196-3199.
( 0) 0)
|
| [6] |
MENSCHIK F. The hip joint as a conchoid shape[J].
Journal of Biomechanics,1997, 30 (9) : 971-973.
( 0) 0)
|
| [7] |
PANCANTI A, BERNAKIEWICZ M, VICECONTI M. The primary stability of a cementless stem varies between subjects as much as between activities[J].
Journal of Biomechanics,2011, 38 (9) : 777-785.
( 0) 0)
|
| [8] |
何荣新. 全髋关节置换前后股骨应力变化的三维有限元分析[J].
中华医学杂志,2012, 6 (18) : 1549-1552.
( 0) 0)
|
| [9] |
NORMAN T L, THYAGARAJAN G. Stem surface roughness alters creep induced subsidence and taper-lock in a cemented femoral hip prosthesis[J].
Journal of Biomechanics,2001 : 1325-1333.
( 0) 0)
|
| [10] |
毛宾尧, 庞清江, 吕厚山, 等.
人工髋关节外科学[M]. 北京: 人民卫生出版社, 2011 .
( 0) 0)
|
| [11] |
王超. 无柄髋假体的设计方法研究及有限元分析[D]. 重庆:重庆大学, 2006.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


