备件是大型机械设备正常运作的保障性物资,必须保证适量且及时的备件供应,高效的备件库存管理与供应对提高企业的经济效益具有重要意义[1]. 其中,备件需求量的确定是备件库存管理的前提. 影响备件需求的原因是多方面的,除了备件的可靠性之外,备件的使用、维护方式及维修策略等均可能影响备件的需求量. 受这些复杂关系的影响,不同备件的历史需求数据特征差异较大,需要针对备件的需求模式研究合适的需求预测方法[2]. 本文研究对象为需求模式呈周期性变化的备件,即其历史需求时间序列中含有随机性成分和周期性成分. 需求时间序列中含有周期性成分和随机性成分时,基于时间序列的预测方法一般分为2类,第1类是使用ARIMA模型[3],这样就剔除了历史需求数据中的周期性成分,从而遗漏了数据中的重要信息[4]. 第2类是将周期性成分分离出来,如Holt-Winters模型[5]以及改进的Holt-Winters模型[6-7]. 该方法对于初始参数值以及平滑常数的确定仍有一定的困难[8]. Grubb等[9]对Holt-Winters模型进行改进,通过使预测误差最小来获取最佳的平滑常数. Bermúdez等[10]则建立了用于更新季节指数的方程,以此为目标函数,并对平滑常数以及初始值进行优化. Abdesselam等[11]将模糊逻辑应用于Holt-Winters模型,并用实验证明了方法的可行性. 除此之外,针对周期型备件的需求预测,董笑晓[12]提出移动平均周期系数法,即采用系数来表征时间序列中的周期性成分. Boylan等[13]针对历史需求数据不足这一问题,将GSI(group seasonal indices)和ISI(individual seasonal indices)方法结合起来用于预测需求. 对具有季节性的间断型需求,Gamberini等[14]比较了Holt-Winters和ARIMA模型的预测精度.
本文提出对备件实际需求数据按其周期长度进行分段,然后对各段进行多项式拟合以提取周期项,为消除随机因素的影响,对各个周期段的多项式函数进行合成得到新的多项式函数,以此来计算下一个周期的需求量预测值.
1 周期长度检测通常备件的需求数据虽然呈现出一定的周期性,但是其周期性并不是表现为以周期间隔的需求数据相等,而是具有相似的波动形式. 假定时间序列X=(x1,x2,…,xn),对于时间序列中以周期间隔的两个数据,如果有xt+T=xt+εt,其中εt为独立的随机变量,则说明该时间序列是周期为T的隐周期序列[15]. 为获得隐周期时间序列的周期长度,一般是将时间序列等分成N段,分别比较各段时间序列的相似度,如果平均相似度满足一定的阈值,则说明时间序列存在该长度的周期. 因此,为检测时间序列的周期,最重要的是解决如何准确的度量时间序列的相似度这一问题.
1.1 时间序列的相似性度量在相似性度量的研究中,大部分采用欧式距离来度量两个时间序列的相似性,距离度量值越小,则两个时间序列越相似. 对于两个等长的时间序列H=(h1,h2,…,hm)和L=(l1,l2,…,lm),H是目标时间序列,L是需要进行相似度测量的时间序列,则这两个时间序列之间的欧式距离定义为
| $d\left( H,L \right)=\frac{1}{m}\sqrt{\sum\limits_{i=1}^{m}{{}}{{\left( {{h}_{i}}-{{l}_{i}} \right)}^{2}}}.$ | (1) |
但是,式(1) 只是表征了两个时间序列在距离上的接近程度,并未体现其动态变化趋势. 两个数据的相似性也表现为它们的整体波动趋势一致,具有一定的相关性,因此可以用相关系数作为相似性度量的另一个量值. 当相关系数>0时,表现为正相关,即H上升,L也上升,H下降,L也下降,此时具有较大的相似度. 当相关系数 <0时,表现为负相关,此时,两序列相似度较小. 在计算相似度时,需要同时考虑两时间序列的欧式距离和相关系数. 因此,对两个长度相等的时间序列H=(h1,h2,…,hm)和L=(l1,l2,…,lm),其相似性度量函数为
| $f\left( H,L \right)=d\left( H,L \right)-\rho HL.$ | (2) |
用式(2) 计算两个时间序列的相似度,当f(H,L)≤α时,则认为两个时间序列具有相似性.
1.2 基于相似度的周期长度检测给定时间序列X=(x1,x2,…,xn),设序列H=(xt,xt+1,…,xt+T-1)为原始时间序列中的T片段,则序列集合{(x1+K*T,x2+K*T,…,x(K+1) *T)|K=0~[n/T]}([·]表示取整)为时间序列X的T片段集合,计为XT. 对于时间序列X=(x1,x2,…,xn),当时间长度为T时,时间序列X按照时间长度T分段后,该时间序列的T片段集合XT的平均相似度为
| $F\left( T \right)=\frac{2}{\left[ n/T \right]\left( \left[ n/T \right]-1 \right)}\sum\limits_{{{H}_{i}},{{H}_{j}}\in XT}{f}\left( {{H}_{i}},{{H}_{j}} \right),$ | (3) |
那么X的周期T-的计算公式为
| $\bar{T}=\min \left\{ F\left( T \right)\left| T \right.=a\sim b且F\left( T \right)\le \alpha \right\}.$ | (4) |
式中: a=1,b=[n/2],阈值α为均值或中值的10%左右.
对于周期T-的求解,当时间序列比较长时,此时给出的周期长度取值范围比较大,若采用穷举法来试探出周期长度,计算量就比较大,需要给出优化算法来近似求出周期长度. 周期长度的取值在a和b之间,因此其搜索方向已经确定,当采用可变的步长进行搜索时,能较快地搜索出周期长度的值. 以式(4) 为目标函数,则搜索步骤为:
1) 设定步长h,在区间[a,b]之间以步长h进行搜索,即令Tn=a+n*h(其中n=1,2,…,[(b-a)/h]),代入式(3) 中并比较F(Tn)的大小;
2) 根据目标函数(式(4) )选出相对较优的前m个时间长度Tn,重新标记为T1,T2,…,Tm;
3) 分别以T1,T2,…,Tm为中心,搜索宽度为中心左右两边各h/2的范围,以步长h/4在中心左右两边分别进行搜索,即令Tn=Tm+n*h/4(其中n∈[-2,2],n为整数),代入式(3) 中并比较F(Tn)的大小;
4) 根据目标函数(式(4) )选出相对较优的前l(l <m)个时间长度Tn,重新标记为T1′,T2′,…,Tl′;
5) 以同样方式进行搜索,直到步长缩减为1,根据目标函数(式4) 选出最优的T值,即为时间序列的周期长度T-.
2 预测模型的建立由前文得到时间序列的周期长度,则可以将整个时间序列按照其周期长度划分成各个周期段. 各个周期段内的函数解析表达式未知,只是已知其上m个数据点(xi,yi),i∈[1,m],为提取各个周期段内的周期函数,需对已知的各个周期内的数据点进行函数拟合. 对于各个周期段内的历史需求数据,由于各个周期内的备件需求受到的外界因素影响是不一样的,因此,由拟合函数所提取的周期项并不能代表整个时间序列上的周期趋势. 为消除随机因素的影响,可将各个周期段内的拟合函数进行合成,得到一个新的拟合函数,综合所有周期内的需求趋势,以此作为整个时间序列上的周期项表达式.
2.1 多项式函数拟合各个周期段内的离散数据点比较少,而多项式拟合方法简单有效,应用广泛,本文采用多项式拟合离散需求数据. 设φ为所有次数不超过n(n≤m)的多项式构成的函数类,对数据点(xi,yi)(i∈[1,m])拟合,即求
| $p\left( x \right)=\sum\limits_{k=0}^{n}{{{a}_{k}}{{x}^{k}}\in \varphi ,\left( k=0,1,...,n \right),}$ |
使得
| $I=\sum\limits_{i=0}^{m}{{{\left[ p\left( {{x}_{i}} \right)-{{y}_{i}} \right]}^{2}}}={{\sum\limits_{i=0}^{m}{\left( \sum\limits_{k=0}^{n}{{{a}_{k}}x_{i}^{k}-{{y}_{i}}} \right)}}^{2}}$ |
最小.
上述问题的求解最终可转换为求极值的问题,最后可以求解出参数ak(k=0,1,···,n)的值,得到拟合多项式的表达式:
| $p\left( x \right)={{a}_{k}}{{x}^{k}}+{{a}_{k-1}}{{x}_{k-1}}+...+{{a}_{1}}x+{{a}_{0}}.$ | (5) |
空间中任意多个向量采取两两合成的方法最终可以合成一个向量,由多个函数最终合成为一个函数也可以借鉴向量合成的思想. 对于时间序列中任意两个周期段内的多项式拟合函数,获取函数的特征集合,函数的特征即为能够将函数区分开来的对象,可以利用向量合成的方式将多个函数特征集合合成为一个新的特征集合,合成的新特征集合再还原成一个新的多项式拟合函数,这就将多个函数合成转换为对函数特征集合的合成.
2.2.1 多项式函数的特征集合各周期段内的离散数据点均采用多项式进行拟合,拟合函数的表达式为$p\left( x \right)=\sum\limits_{k=0}^{n}{{{a}_{k}}x_{i}^{k}}$,则各周期段的拟合函数可以认为是以xk(k=0,1,…,n)为基函数的线性加权求和. 当各个周期段对离散数据点的拟合采用相同的拟合次数时,可以认为拟合各周期段离散数据点的函数表达式形式相同,区别各个周期段拟合函数的特征量即为基函数的系数,因此可以将基函数的系数视作函数的特征量.
以$f\left( x \right)=\sum\limits_{i=0}^{n}{{{h}_{i}}{{{\bar{x}}}_{i}}}+{{h}_{0}}$为参照,式(5) 建立了一个n维坐标空间中的超平面,xk相当于坐标空间中第i维坐标xi,系数ak相当于坐标值hi,常量h0为平移量. 在表达式(5) 中,取系数ak为函数特征,周期段的多项式函数的特征集合为{an,an-1,…,a0}. 对各周期段多项式函数的合成可以通过对多项式函数特征集合的合成来实现.
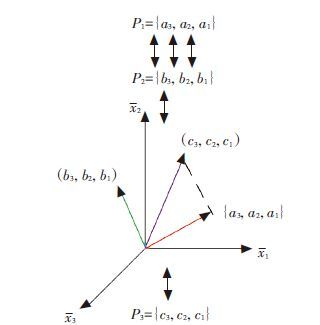
2.2.2 基于特征集合合成的函数合成对于两个函数的合成过程,以多项式次数为3时的两个周期函数为例进行解释,过程如图 1所示.
|
图 1 特征集合合成过程 |
第1个和第2个周期段内的数据点经拟合后得到的多项式函数表达式分别为
| $\begin{align} & {{p}_{1}}\left( x \right)={{a}_{3}}{{x}^{3}}+{{a}_{2}}{{x}^{2}}+{{a}_{1}}{{x}^{1}}+{{a}_{0}}, \\ & {{p}_{2}}\left( x \right)={{b}_{3}}{{x}^{3}}+{{b}_{2}}{{x}^{2}}+{{b}_{1}}{{x}^{1}}+{{b}_{0}}. \\ \end{align}$ |
这两个函数的特征集合分别为
| $\begin{align} & {{p}_{1}}=\left\{ {{a}_{3}},{{a}_{2}},{{a}_{1}},{{a}_{0}} \right\}, \\ & {{p}_{2}}=\left\{ {{b}_{3}},{{b}_{2}},{{b}_{1}},{{b}_{0}} \right\}, \\ \end{align}$ |
系数ak和bk(k=1,2,3) 相当于坐标空间中第i维坐标xi上的坐标值,按照向量合成模式,则新合成的特征集合为对应的坐标值之和取平均. 设新的特征集合为
| ${{p}_{3}}=\left\{ {{c}_{3}},{{c}_{2}},{{c}_{1}},{{c}_{0}} \right\},{{c}_{k}}=\left( {{a}_{k}}+{{b}_{k}} \right)/2,\left( k=0,1,2,3 \right).$ |
最后根据合成的新特征集合还原成新的多项式函数为
| ${{p}_{3}}\left( x \right)={{c}_{3}}{{x}^{3}}+{{c}_{2}}{{x}^{2}}+{{c}_{1}}{{x}^{1}}+{{c}_{0}}.$ |
考虑到历史需求数据信息对预测未来周期段内的备件需求量的作用是不一样的,对于新合成函数特征值的计算采用加权求和法,而不是求和取平均,即ck=w1ak+w2bk,其中0, <w1 <1,<w2 <1,且w1+w2=1. 权重一般比较难以确定,并且权重的取值直接影响模型的预测精度,需要慎重选择. 因此,在本文中,以历史需求数据的预测值和实际值的平均相对误差最小为优化目标,建立式(6) 所示的优化模型:
| $\begin{align} & min\text{ }ac=\frac{1}{n}\sum\limits_{i=1}^{n}{\frac{\left| {y}'\left( {{w}_{1}} \right){{y}_{i}} \right|}{{{y}_{i}}}}, \\ & \text{s}\text{.t}\text{.}{{w}_{1}}\text{ }\in \left( 0,1 \right). \\ \end{align}$ | (6) |
式中: yi为实际需求数据,yi′(w1)为对应的预测值,采用应用较广的遗传算法求解权重.
3 实验验证 3.1 人工数据验证试验所采用的数据由SinSeries数据产生器产生,该数据产生器为
| ${{x}_{t}}=A\times \sin \left( t/T \right)+B+{{\varepsilon }_{t}},\text{ }{{\varepsilon }_{t}}\sim N\left( {{\mu }_{i}},{{\sigma }_{i}} \right).$ |
式中: μi、σi为随机数,A=80,T=3,B=300,μ=0,σ=20. 截取xi中的45个数据作为样本数据. 周期长度的取值范围为1~23,阈值为均值的10%,用1.2节中的周期长度检测算法计算得到序列的周期长度为9. 将样本数据分成5个数据段,以前面4个周期段的数据建立备件需求预测模型,用该预测模型计算第5个周期段的需求. 当n=6时,计算得到的第4个周期段的需求预测值与实际值的误差最小,因此选择拟合多项式n=6. 以第4个周期段的预测值的平均相对误差最小为优化函数,采用遗传算法确定权值为w1=0.41,w2=0.29,w3=0.30. 确定多项式拟合次数和权值后,则可建立需求预测模型.
对周期段2、3、4的离散数据进行拟合,得到各段的拟合多项式函数,表 1中第2~4行分别是这3个周期段拟合多项式函数的特征值. 通过加权合成方式得到新的特征值为dn=0.41an+0.29bn+0.3cn,即表 1中第5行所示数据.
| 表 1 多项式函数的特征值 |
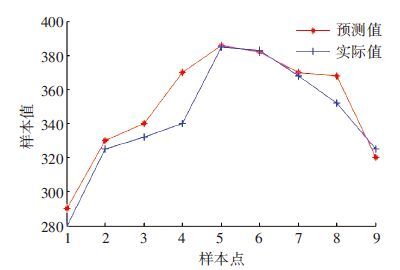
用新合成的特征值还原成多项式函数,以此作为预测模型用于预测第5个周期段的数据,预测结果如图 2所示. 实验表明,预测值与实际值的平均相对误差为7.4%.
|
图 2 预测值与实际值比较 |
运用该方法对矿用高强度圆环链的需求进行预测,并与文献[12]中的移动平均周期系数法进行对比分析. 圆环链为采煤机的备件,实验数据来自文献[16],为2007年1月~2010年12月计4年的数据.
已知备件历史需求数据,周期长度T的取值范围为1-24,阈值α为备件需求数据均值的10%,通过1.2节的周期长度检测算法计算得出备件需求时间序列的周期为12. 按照周期长度将样本数据分成4个周期段,以前面3个周期段的数据建立备件需求预测模型,使用所建立的预测模型计算最后12个月的备件需求量,并和需求实际值进行对比. 在建立周期需求预测模型时,需要确定的参数为多项式的拟合次数n,拟合次数n可以通过实验获得. 遍历拟合次数n可能的值,选择使得第3个周期段的预测值和实际值的预测误差最小的拟合次数,以此作为最佳的多项式拟合次数. 表 2列出了各数值对应的预测误差,可以看出,当多项式次数为n=11时,预测误差最小,因此,采用多项式回归模型拟合备件需求数据时,多项式次数为n=11.
| 表 2 各多项式次数对应的预测误差 |
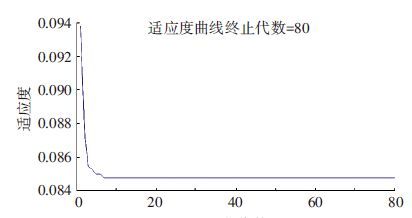
对第1、2周期段的离散需求数据分别进行多项式拟合,提取其特征集合,集合中的元素分别设为an和bn,采用加权求和的方式来合成新的特征集合,即dn=w1an+w2bn,其中,0≤w1≤1,0≤w2≤1,w1+w2=1,式(6) 为优化目标,yi为第3个周期段的需求数据,并采用遗传算法求解w1和w2. 设置遗传算法的初始种群为80,迭代次数为80,适应度函数为式(6) ,交叉概率为0.3,变异概率为0.7,编码方式为浮点数编码、选择方式为比例选择,交叉方式为线性交叉,变异方式为扰动变异. 遗传算法求解结果如图 3所示,求得w1=0,则w2=1.
|
图 3 遗传算法求解结果 |
以上过程通过对前3个周期段的数据分析确定了预测模型的多项式拟合次数n=11,权值w1=0,w2=1. 当这些参数确定后,则可以建立周期型需求模式的备件需求预测模型. 对第2、3个周期段内的离散数据进行多项式拟合,提取多项式函数的特征集合,特征集合中的元素分别设为an′和bn′,如表 3所示.
| 表 3 各周期段多项式函数的特征值表 |
采用加权求和的方式来合成新的特征集合,即dn′=w1an′+w2bn′,故dn′=bn′. 合成后的特征值如表 3中第4行所示.
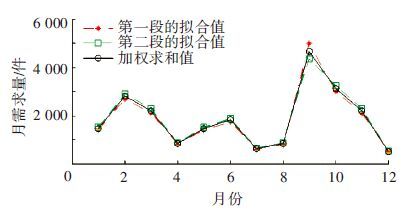
合成得到的新的特征集合还原成新的多项式函数,此多项式函数即为需求预测模型,各周期段的加权合成过程如图 4所示. 应用该模型计算2010年12个月的备件需求量数据,预测结果如图 5所示,可以看出预测值比较接近实际值.
|
图 4 周期段的加权合成 |
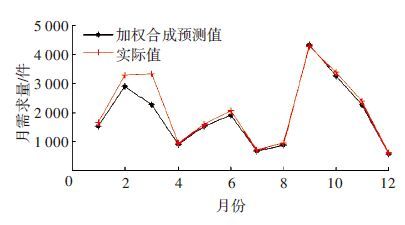
|
图 5 多项式拟合模型的预测结果 |
本文所述预测模型与移动平均周期系数法的预测结果比较如表 4所示.
| 表 4 两种预测模型结果对比 |
从表 4中的数据可以计算出,移动平均周期系数法的预测值与实际值的平均绝对误差为286.8,平均相对误差为12.8%. 多项式拟合模型的预测值与实际值的平均绝对误差为199.6,平均相对误差为8.9%. 因此可以看出本文提出的预测模型的预测效果更好.
4 结论与展望1) 针对需求模式为周期型的维修备件需求预测问题,本文提出了一种新的需求预测方法. 用预测模型对人工数据和矿用圆环链的需求量进行预测,实验结果表明,该预测方法具有较高的预测精度.
2) 维修备件的种类非常多,对于不同种类的维修备件,其需求数据的波动形式会有较大区别,有时其周期成分比较弱,可能会被随机成分遮掩,此时,本文所提的预测方法并不适用. 因此,针对不同形式的维修备件需求数据,探讨新的建模方法,仍然是今后需要深入研究的工作.
| [1] |
王林, 富庆亮, 曾宇容. 基于遗传和差分进化算法的备件库存协同控制模型[J].
计算机集成制造系统,2010, 16 (10) : 2257-2264.
( 0) 0)
|
| [2] |
NEZIH A.
Service parts management: demand forecasting and inventory control[M]. New York: Springer Verlag GMBH, 2011 : 89 -101.
( 0) 0)
|
| [3] |
王振龙.
时间序列分析[M]. 北京: 中国统计出版社, 2000 : 45 -50.
( 0) 0)
|
| [4] |
采峰, 曾凤章. 产品需求量非平稳时序的ANN-ARMA预测模型[J].
北京理工大学学报,2007, 27 (3) : 277-282.
( 0) 0)
|
| [5] |
WINTERS P R. Forecasting sales by exponentially weighted moving averages[J].
Management Science,1960, 6 (3) : 324-342.
( 0) 0)
|
| [6] |
VINKO L, MARIJA A. Forecasting electricity consumption by using Holt-Winters and seasonal regression models[J].
Economics and Organization,2011, 8 (4) : 421-431.
( 0) 0)
|
| [7] |
LEE M H, NOR M E, SUHARTONO, et al. Fuzzy time series: an application to tourism demand forecasting[J].
American Journal of Applied Sciences,2012, 9 (1) : 132-140.
( 0) 0)
|
| [8] |
BERMúDEZ J D, SEGURA J V, VERCHER V E. A decision support system methodology for forecasting of time series based on soft computing[J].
Computational Statistics & Data Analysis,2006, 51 (1) : 177-191.
( 0) 0)
|
| [9] |
GRUBB H, MASON A. Long lead-time forecasting of UK air passengers by Holt-Winters methods with damped trend[J].
International Journal of Forecasting,2001, 17 (1) : 71-82.
( 0) 0)
|
| [10] |
BERMúDEZ J D, SEGURA J V, VERCHER V E. Holt-winters forecasting: an alternative formulation applied to UK air passenger data[J].
Journal of Applied Statistics,2007, 34 (9) : 1075-1090.
( 0) 0)
|
| [11] |
ABDESSELAM M, KARIM A N M, KAYS H M E, et al. Forecasting demand: development of a fuzzy growth adjusted Holt-Winters approach[J].
Advanced Materials Research,2014, 903 : 402-407.
( 0) 0)
|
| [12] |
董笑晓. 基于需求预测的轨道交通备件库存控制研究[D]. 上海: 上海交通大学, 2012: 30-34.
( 0) 0)
|
| [13] |
BOYLAN J E, CHEN H, MOHAMMADIPOUR M, et al. Formation of seasonal groups and application of seasonal indices[J].
Journal of the Operational Research Society,2014, 65 (2) : 227-241.
( 0) 0)
|
| [14] |
GAMBERINI R, LOLLI F, RIMINI B,et al. Forecasting of sporadic demand patterns with seasonality and trend components: an empirical comparison between Holt-Winters and (s)ARIMA methods[J/OL]. Mathematical Problems in Engineering, 2010. DOI: 10.1155/2010/579010.
( 0) 0)
|
| [15] |
李晓光, 宋宝燕, 于戈, 等. 基于小波的时间序列流伪周期检测方法[J].
软件学报,2010, 21 (9) : 2161-2172.
( 0) 0)
|
| [16] |
李志. 基于支持向量机的兖矿集团备件需求研究[D]. 青岛: 中国海洋大学, 2012: 38.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


