车身封闭件(包括车灯、引擎盖、行李箱盖、车门等)的外形设计随着消费者审美需求的提高,逐渐从传统的规则形状发展为三维复杂外形面[1]. 这种复杂形面在匹配过程中,由车身封闭件的形面边界和白车身本体的形面边界构成的缝隙和面差往往很难通过人工测量进行准确评估. 另外,传统匹配方法[2-5]的匹配数据主要来源于三坐标测量机,只能在一定的时间内测量有限个测点,同时由于受到了测量物体本身的定位偏差、制造偏差以及装配偏差等影响,这些测点只能部分表达被测物体匹配边界的状态;相比之下,通过点云扫描设备获得的点云数据就可以更好地反映出匹配边界的特性,通过对复杂形面边界特征提取,可以进一步优化复杂形面之间的姿态匹配.
点云边界特征的提取在逆向工程领域应用较多,直接从点云提取边界特征的方法主要有两类. 一类是基于切边特征的提取方法,柯映林等[6]对点云数据进行了栅格化划分,识别出种子边界栅格,根据空间拓扑构型连接边界栅格,由于采用了拓扑逻辑判断算法,提高了边界提取效率和稳定性,但是栅格划分的大小会对边界特征的精度产生一定影响;孙殿柱等[7]提出了散乱数据点云边界特征自动提取算法,对散乱点云数据采用R-tree结构进行空间索引,进而提取参考点附近的 k 个最近点,建立参考点的微切平面,针对微切平面上的参考点及其最近点的投影连线,用判断最大邻近向量夹角的方法识别出散乱点云的边界. 陈义仁等[8]用三维排序的方法建立索引,用场力大小来判断投影点集是否位于曲面边界,提高了算法运算速度. 另一类是基于交线特征的提取方法[9-13]. Pauly等[9]针对局部邻域进行协变量分析潜在的特征点,通过改变邻域半径大小,可以实现不同精度的数据处理结果. 张旭等[10]提出的基于模板的点云特征提取技术,由理论模型在计算机辅助设计下生成理论交线上的离散点和切矢量,进而在模板上切片获得截面用于二维数据分析,并以理论离散点为分界依据,将截面数据分成两段后拟合获得两段曲线交点,即边界交线特征上的点. Gumhold等[11]在邻域中建立了黎曼图,同样采用了协方差分析的方式标记潜在交线特征. 两种方法都使用最小生成树连接特征点,并用曲线拟合的方式最终获得近似的边界特征. Demarsin等[12]使用主成分分析法计算点的法向量,并通过邻域的法向偏差对点云进行分割,同时也采用了最小生成树法连接边界点. Daniels等[13]采用移动最小二乘法对点云数据进行光滑特征的提取,从特征点中构建边界交线,最后连接相邻的边界交线,形成封闭光滑的特征线. 在这两类方法中,前者针对有界点云数据的边界进行提取,后者则对点云数据中造型面之间的交线进行提取,两类特征的提取方法有很大的差异. 此外这些研究主要用于提取扫描对象的边界点集,从而得到简化模型,实现对扫描对象的曲面重构及逆向造型.
本文针对具有复杂外形面的车身封闭件匹配这一问题,提出了通过提取复杂形面轮廓边界的空间坐标及其表面信息的方法,为复杂形面边界进一步匹配优化提供依据.
1 复杂形面的边界特征按照边界形成的成因来分类,复杂形面的边界曲线可以分为两类,一类是由单个曲面的边界自然形成的,如钣金件切边、车灯的边界等;另一类是两个曲面相交时产生的交线,如车身上的对应匹配区域由于冲压、铸造、翻边或者折边等工艺形成的交线.
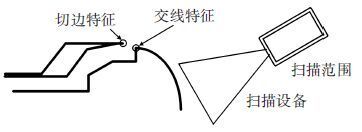
如图 1所示,典型的匹配断面既包含切边形成的匹配边界,也包含交线形成的匹配边界. 对于交线特征,从扫描设备的视角来看,当扫描范围只覆盖匹配侧外表面时,其匹配边界即为切线特征. 因此,对于交线特征的表面,可以通过规范扫描设备的扫描路径将其转化为切边边界特征,从而形成统一的边界形式进行边界特征提取.
|
图 1 典型匹配断面图 |
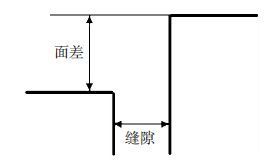
传统车身封闭件与车身装配后通过装配体之间缝隙的大小和外表面之间面差的大小来评价两者之间的匹配质量(如图 2所示). 简单形面可以使用塞尺和面差计人工测量,进行评价,但是对于三维复杂形面之间的匹配,肉眼难以定量地确定形面之间的匹配关系. 边界点本身的空间坐标位置只能表达两个边界点之间相对的位置关系,匹配得好坏还需要通过缝隙和面差的大小来进行评价.
|
图 2 车身封闭件匹配评价指标 |
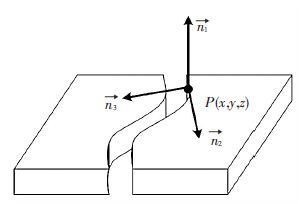
由于车身的外部造型必须要符合A级曲面的要求. 从曲面的特性来看,A级曲面的要求可以表述为:1) 匹配对应点和对应曲线处的角度变化为零;2) 曲面满足G2(二阶可微)或G3(三阶可微)连续. 在这个前提下,两个匹配对象的对应点具有相同的曲面特征和边界曲线特征. 边界点所在面的法向量 ${{\vec{n}}_{1}}$ 决定了计算面差的矢量方向,边界点所在边界曲线的切线 ${{\vec{n}}_{2}}$ 与法向量 ${{\vec{n}}_{1}}$ 的叉积 ${{\vec{n}}_{4}}$ 决定了计算缝隙的矢量方向. 如图 3所示,用于形面匹配的边界特征包括边界点坐标 (x,y,z) 及其匹配局部坐标系向量 (${{\vec{n}}_{1}},{{\vec{n}}_{2}},{{\vec{n}}_{3}}$). 对于复杂形面匹配,实现边界特征的提取可以定量评估匹配的质量,是复杂形面匹配优化的关键步骤.
|
图 3 边界任意一点处的匹配特征 |
匹配特征提取方法基本流程包括以下步骤:使用 树(多维二叉树)建立二叉数据分类和索引结构,将每个数据存储在每个节点中,可以实现邻近点的搜索[14];通过对复杂形面的分析,确定采样间距和特征搜索邻域;通过邻域内邻近点的位置关系,确定匹配边界特征,并提取相应的空间坐标和形面的向量特征.
2.1 采样间距和特征搜索邻域的确定对于复杂形面,通过扫描得到的点云数据往往是由几次扫描数据拼合而成的. 具有完整表面信息的点云数据通常是散乱点云,因此需要对点云数据进行稀释和均一化处理.
对于匹配边界特征的邻域,首先要考虑的是采样原则. 一方面通过均匀采样可以保证散乱点云数据的有序规范;另一方面采样间距的大小决定了最终的匹配效果,采样间距越小,综合匹配效果越好,但是也会造成计算量的增加,从而影响匹配效率.
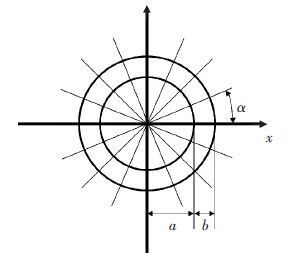
对于任意一条曲线,其局部都可以用一段圆弧来近似表达,而圆弧则可以用多个直线段来逼近. 如图 4所示,假设有两个匹配体为二维圆形, 半径分别为a和a+b,那么其直接的理论缝隙量为b. 当两个二维的匹配圆形被划分成n段圆弧时,其每段圆弧所对应的夹角为α. 那么第k(其中k=1,2,3,…,n)段内圈圆弧所对应的起点坐标为(acos((k-1) α),asin((k-1) α)),终点坐标为(acos(kα),asin(kα)), 而外圈圆弧所对应的起点坐标为 ((a+b)cos(k-1)α),((a+b)sin(k-1)α), 终点坐标为 ((a+b)cos(kα),(a+b)sin(kα)). 其所对应的圆弧近似线段矢量分别为
内圈, (acos(kα)-acos(k-1)α,asin(kα)-asin((k-1)α)),
外圈, ((a+b)cos(kα)-cos(k-1)α,(a+b)sin(kα)-sin((k-1)α))),
| ${{\vec{l}}_{uniform}}=\left( -\sin \left( \frac{2k-1}{2}\alpha \right),\cos \left( \frac{2k-1}{2}\alpha \right) \right).$ | (1) |
式(1) 代表每条圆弧近似直线段的单位向量,而其法向方向,则可以表示为
| $\vec{n}=\left( \cos \left( \frac{2k-1}{2}\alpha \right),\sin \left( \frac{2k-1}{2}\alpha \right) \right).$ |
|
图 4 线段拟合匹配边界示意 |
进一步对内外圈圆弧近似直线段的缝隙间距 d 进行计算:
| $\begin{align} & d=\left| \vec{n}\cdot \left( {{l}_{out,end}}-{{l}_{in,end}} \right) \right|= \\ & \left| \vec{n}\cdot \left( b\cos \left( k\alpha \right),b\sin \left( k\alpha \right) \right) \right|= \\ & \left| \left( \cos \left( \left( 2k-1 \right) \right.\alpha /2 \right),\sin \right.\left. \left( \left( 2k-1 \right)\alpha /2 \right) \right)\cdot \\ & \left( b\cos \left( k\alpha \right),b\sin \left( k\alpha \right) \right)\left| =b\left| \cos \alpha /2 \right|. \right. \\ \end{align}$ | (2) |
由式(2) 推导结果可知,对于匹配圆形,其圆弧近似直线段由理论缝隙值 b 和最小采样角 α 决定,由于一般缝隙值 b 为恒定值,因此最小采样角 α 的大小对采样间距起到了决定作用. 当 α≤5° 时, cos(α/2)=0.999 $0\simeq 1$, 此时用直线段来近似圆弧段用于缝隙匹配即可达到很好的效果. 当采样线段 $\left| {\vec{l}} \right|<\alpha r\le \pi r/36$ (其中 r 表示该弧线段的曲率半径)时可满足匹配需要,因此可以通过减少所需处理的点云数据数量的方法,提高后续数据处理效率;而匹配边界特征提取的邻域大小可用2倍采样间距表征,即 πr/18.
2.2 匹配边界特征提取扫描点云中包含着大量的坐标数据信息,按照匹配需求可划分为两类:一类是具有匹配功能的边界点;另一类是对匹配贡献度较小的面点,这一类点云数据在数据处理中属于冗余信息,需要进行剔除,留下边界点云用于下一步的处理.
提取的目标边界特征点需要包含两个方面的信息,即空间坐标 (x,y,z) 和匹配局部坐标系向量 (${{\vec{n}}_{1,}}{{\vec{n}}_{2,}}{{\vec{n}}_{3}}$) . 结合文献[7-8]提出的点云边界特征提取方法,给出了面向复杂形面匹配的特征提取方法.
根据前文讨论结果,以 πr/18 为邻域搜索半径,应用 k-d 树建立的索引对点云每一点的邻域点进行搜索,以该邻域内的点作为该点的局部参考面的点集,采用最小二乘法对该点集进行拟合.
方程 F(x,y,z)=a1x+a2y+a3z+a4 ,将邻域点集代入方程,有
| $F\left( x,y,z \right)=\left[ \begin{matrix} {{x}_{0}} & {{y}_{0}} & {{z}_{0}} & 1 \\ {{x}_{1}} & {{y}_{1}} & {{z}_{1}} & 1 \\ \vdots & \vdots & \vdots & \vdots \\ {{x}_{k}} & {{y}_{k}} & {{z}_{k}} & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{a}_{1}} \\ {{a}_{2}} \\ {{a}_{3}} \\ {{a}_{4}} \\ \end{matrix} \right].$ | (3) |
此时,求方程(3) 最小二乘解,将点集的坐标阵扩展成满秩矩阵,对其进行奇异值分解得到最小特征值的特征向量 υmin, 即平面方程参数的最小二乘解 aLS.
| $\begin{align} & {{\left[ \begin{matrix} {{x}_{0}} & {{y}_{0}} & {{z}_{0}} & 1 \\ {{x}_{1}} & {{y}_{1}} & {{z}_{1}} & 1 \\ \vdots & \vdots & \vdots & \vdots \\ {{x}_{k}} & {{y}_{k}} & {{z}_{k}} & 1 \\ \end{matrix} \right]}^{T}}\left[ \begin{matrix} {{x}_{0}} & {{y}_{0}} & {{z}_{0}} & 1 \\ {{x}_{1}} & {{y}_{1}} & {{z}_{1}} & 1 \\ \vdots & \vdots & \vdots & \vdots \\ {{x}_{k}} & {{y}_{k}} & {{z}_{k}} & 1 \\ \end{matrix} \right]= \\ & U\left[ {{v}_{1}} {{v}_{2}} {{v}_{3}} {{v}_{4}} \right]V. \\ \end{align}$ | (4) |
式(4) 中 U 和 V 为正交矩阵,特征向量用 υi(i=1,2,3,4) 表示. 求解方程式的最小特征值,即可确定方程
| $F\left( x,y,z \right)={{a}_{1}}x+{{a}_{2}}y+{{a}_{3}}z+{{a}_{4}}=0$ |
的最小二乘解的特征向量υmin,即P点处的曲面法向量${{\vec{n}}_{1}}$.
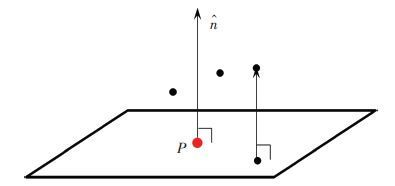
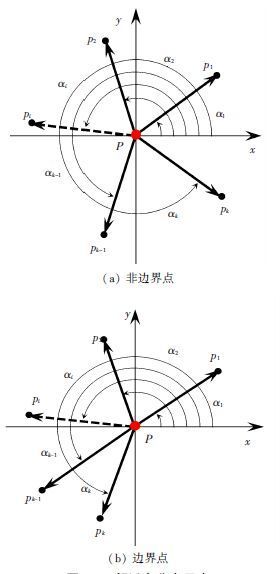
沿着 P点的法向量将点集投影到最小二乘微切平面,得到$X'=\left\{ \left( x_{i}^{'},y_{i}^{'},z_{i}^{'} \right)\left| i=0,1,\cdots \left. k \right\} \right. \right.$,如图 5所示. 进一步地将P点作为原点在最小二乘微切平面上建立局部坐标系,P点的邻近点在局部坐标系上的坐标即为邻近点到P点的向量,考察这些向量之间的角度关系,即可判断当前点P是否为边界点,如图 6所示.
|
图 5 k邻近点、最小二乘平面和法向量示意 |
|
图 6 k邻近点分布示意 |
通过局部坐标系, 计算每一个向量的与x轴的夹角αi(i=1,2,…,k), 并按照大小对其进行排序,相邻向量间的夹角可表示为
| ${{\delta }_{i}}=\left\{ _{{{\alpha }_{1}}-{{\alpha }_{i}}+2\pi ,\left( i=k \right).}^{{{\alpha }_{i+1}}-{{\alpha }_{i}},\left( i=1,2,\cdots k-1 \right);} \right.$ |
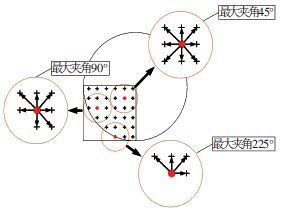
如图 7所示,对图中所示的圆形物体进行均匀采样后,位于边界处的采样点的最大夹角和位于内部的采样点的最大夹角有显著不同. 根据前文确定的邻域大小,计算单个采样点与 k 邻近点组成的向量夹角. 对非边界点,最大夹角为45°,对边界点,最大夹角在90°~225°变化,因此边界点的采样阈值可确定为90°,采样点的最大夹角大于此阈值的即为边界特征点. 由此,具有不同形态特征和采样条件的物体均可以根据以上原则进行数据分析,计算得出合理的夹角阈值,同时通过设定阈值,筛选出最大夹角大于阈值的采样点,从而获得边界点点集.
|
图 7 采样点在邻域内的最大相邻向量夹角 |
边界点点集的确定即基本形面匹配特征的确定,而复杂形面匹配特征仍需进一步处理. 首先是对法向量 ${{\vec{n}}_{1}}$ 的处理,其大小在提取基本边界特征时即已确定,但是每个边界点的法向量方向仍需要进一步协调一致. 在边界点点集中任意取一点,向两个方向寻找最近点,并进行排序,直至终止(不封闭边界点以搜索不到最近点为终止,封闭边界点以搜索到起始点为终止). 根据排序,相邻点之间的法向量乘积若为负,则按照基准点的法向量调整下一点的法向量,直至终止. 其次是确定边界曲线的切向量 ${{\vec{n}}_{2}}$, 在相邻边界点之间间距足够小的情况下,可以用相邻点向量来近似切向量. 最后通过法向量 ${{\vec{n}}_{1}}$ 和切向量 ${{\vec{n}}_{2}}$ 的叉积确定 ${{\vec{n}}_{3}}$, 确定匹配局部坐标系向量,获得完整的复杂形面匹配特征信息.
3 案例分析如图 8所示,以两个半圆柱匹配对象为例,对本文方法进行试验验证. 半圆柱弧面各自以随机生成的散乱点云数据来表征,长圆柱弧面由20 000个随机点构成,而短圆柱弧面则有10 000个随机点构成,匹配边界处圆弧的半径为1.

|
图 8 匹配特征试验对象及其随机点云数据 |
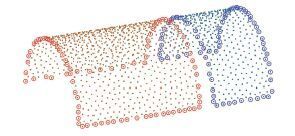
根据前文定义,采样间距应小于 πr/36, 搜索邻域应小于 πr/18, 这里选定采样间距为0.08,搜索邻域为0.16,相邻向量夹角阈值为155°. 稀释前的点云搜索邻域设为0.08,如图 9所示,从长圆柱弧面和短圆柱弧面提取出的边界点数分别为344个和288个,分别耗时287.89 s和127.24 s;边界点稀释后的点云数据如图 10所示,在保留原有特征的同时,长圆柱弧面的点云数量从20 000个减少到了847个;而短圆柱弧面的点云数量则从10 000个减少到了435个. 从稀释后的点云中提取出边界点,数量分别为84和74个,分别耗时3.36 s和1.50 s.

|
图 9 稀释前点云及其边界特征点 |
|
图 10 稀释点云及其边界特征点 |
通过圆柱体案例分析,验证了本方法的可行性和提取效率. 为了进一步验证本方法在工程应用中的有效性,本文对具有复杂形面特点的某车型尾灯的边界进行了研究.
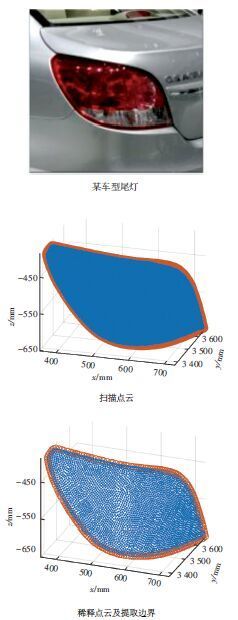
如图 11所示,通过扫描设备对该尾灯的数据进行扫描后得到原始点云数据,初始点云数量为73 050个. 通过对边界点的分析,其主要匹配区域(图中尾灯的左下和右上的边界区域)的边界近似圆弧半径不小于60,因此采样间距设为5,得到稀释后的点云数据,为3 356个. 采用本文方法提取边界特征,搜索邻域距离设为10,相邻向量夹角阈值设为155°,得到边界特征208个,耗时15.82 s;采用文献[7]的方法,搜索最近邻近点设为10个,相邻向量夹角阈值设为155°,得到边界特征210个,耗时615.27 s;显然在初始条件和结果基本一致的情况下,本文方法得到的是动态的邻近点,对于边界点,其邻近点必然少于非边界点的邻近点,因此本文的提取效率比原有方法得到了显著提高.
|
图 11 某车型尾灯的边界提取 |
从简单圆柱和实际尾灯的案例分析中可以发现,对于散乱点云数据,根据其匹配特征定义合理的采样间距对点云数据进行稀释,从而获得均匀分布的点云. 在满足匹配要求的前提下,可以提高边界特征点的提取效率.
4 结论1) 本文针对车身装配中复杂形面的匹配问题,确定了匹配边界的提取目标,并提出了一种适用于复杂形面的边界特征提取方法.
2) 以 k-d 树数据结构为基础,根据复杂形面的匹配特点,确定了采样间距和搜索域的大小,精简了目标点云数据.
3) 通过对采样点在搜索邻域内的邻近点建立最小二乘微切平面,分析邻近点投影到微切平面局部坐标系后的分布特性,从而确定边界特征点并提取匹配所需信息,包括边界点坐标及其匹配局部坐标系向量.
4) 通过案例分析,对本方法进行了验证. 在不影响匹配效果的前提下,其匹配边界的提取效率得到显著提高,为复杂形面匹配过程中分析、评估、优化提供了数据基础.
| [1] |
GAO X, WANG H, CHEN G. Fitting optimization based on weighted Gaussian imaging method for auto body taillight assembly[J].
Assembly Autom,2014, 34 (3) : 255-263.
( 0) 0)
|
| [2] |
WU S K, HU S J, WU S M. Optimal door fitting with systematic fixture adjustment[J].
International Journal of Flexible Manufacturing Systems,1994, 6 (2) : 99-121.
( 0) 0)
|
| [3] |
FAINBERG Z, ZUSSMAN E. Even fitting closed curves: 2-D algorithm and assembly applications[J].
Journal of manufacturing science and engineering,1999, 121 (2) : 265-272.
( 0) 0)
|
| [4] |
许技科, 王华, 郑恒雍, 等. 基于分段 Hausdorff 距离的车身前脸匹配优化[J].
上海交通大学学报,2010, 44 (4) : 0535-0539.
( 0) 0)
|
| [5] |
GAO X, WANG H, CHEN G. Curve fitting optimization based on a mixed model for assembly applications[J].
Journal of Intelligent Manufacturing,2015, 26 (6) : 1113-1120.
( 0) 0)
|
| [6] |
柯映林, 范树迁. 基于点云的边界特征直接提取技术[J].
机械工程学报,2004, 4 (9) : 116-120.
( 0) 0)
|
| [7] |
孙殿柱, 范志先, 李延瑞. 散乱数据点云边界特征自动提取算法[J].
华中科技大学学报(自然科学版),2008, 36 (8) : 82-84.
( 0) 0)
|
| [8] |
陈义仁, 王一宾, 彭张节, 等. 一种改进的散乱点云边界特征点提取算法[J].
计算机工程与应用,2012, 48 (23) : 177-180.
( 0) 0)
|
| [9] |
PAULY M, KEISER R, GROSS M. Multi-scale feature extraction on point-sampled surfaces[J].
Computer Graphics Forum,2003, 22 (3) : 281-289.
( 0) 0)
|
| [10] |
张旭, 王青, 柯映林. 基于模板的点云边特征提取技术[J].
计算机集成制造系统,2008, 14 (6) : 1175-1181.
( 0) 0)
|
| [11] |
GUMHOLD S, WANG X, MACLEOD R. Feature extraction from point clouds [C]//Proceedings of the 10th International Meshing Roundtable. Newport Beach: Sandia National Laboratories, 293-305.
( 0) 0)
|
| [12] |
DEMARSIN K, VANDERSTRAETEN D, VOLODINE T, et al. Detection of closed sharp edges in point clouds using normal estimation and graph theory[J].
Comput Aided Design,2007, 39 (4) : 276-283.
( 0) 0)
|
| [13] |
DANIELS J, HA L K, OCHOTTA T, et al. Robust smooth feature extraction from point clouds[C]//2007 SMI '07 IEEE International Conference on Shape Modeling and Applications. Lyon: IEEE, 2007: 123-136.
( 0) 0)
|
| [14] |
周培德.
计算几何: 算法分析与设计[M]. 北京: 清华大学出版社, 2000 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


