对煤的热解行为进行描述和预测以及进一步对热解机理进行解释是长久以来人们对热解动力学分析的期望. 目前,非等温法已逐渐成为研究固相反应整体动力学的主要方法,其在数学上可分为积分法和微分法;在操作方式上可分为单一扫描速率法和多重扫描速率法.
单一扫描速率法采用“模式匹配法”求解动力学3因子(活化能、频率因子以及模式函数),由于其在实验操作及数学处理上相对简便,目前在非等温动力学分析中已占据主导地位[1-2].
长久以来,此类方法在预测过程速率和材料寿命以及为反应器设计提供性能参数等工业应用方面均发挥了重要作用,但也有文献报道了其在实际应用方面的某些局限性. 在1996年美国费城第11届国际热分析和量热会议上,ICTAC动力学工作小组发起了一个由各国热分析工作者自愿参加的专题项目,其工作报告[3-7]指出,“许多文献均报导了在单一扫描速率下得到的非等温实验数据能够被几组不同的动力学3因子同时匹配的现象”,同时对CaCO3热分解失重数据的动力学计算表明,不同学者采用不同模式函数计算出的动力学参数差异很大. Vyazovkin等[1]对环四亚甲基四硝基胺(HMX)和二硝酰胺铵(AND)分解失重数据的研究结果也表明,几个不同的模式函数均可与实验数据匹配良好. Budrugeac等[8-10]以单一扫描速率法对单步反应的模拟数据以及聚氯乙烯(PVC)热分解、CaC2O4·H2O加热脱水、醋酸锌凝胶前驱体分解的失重数据进行动力学计算时也出现了相似的情况,且他们由此提出“仅使用统计学标准(即线性相关系数)得不到真实的机理函数”. Marcilla等[11]提出“当体系中有复杂的反应存在而只能在相对窄的转化率范围内进行研究时,使用单一扫描速率法时会有更多的模式函数与实验数据达到良好匹配”. 显然,上述现象使人们无法分辨正确的模式函数,也使动力学参数的评价和比较变得困难. 尽管如此,由于单一扫描速率法突出的实际应用意义,许多学者已将其引入煤热解领域[12-25]. 虽然到目前为止,还未见到对此类方法在煤热解领域的多匹配现象进行详细探讨的文献,但一些动力学计算结果已经显现出端倪. 例如,同为大同烟煤,一些学者计算的热解表观活化能 (E) 值为61.55~239.74 kJ/mol[17],而另一些学者则为6.322~33.591 kJ/mol[18],二者相差6~8倍;同为平朔烟煤,一些学者给出2.942~55.059 kJ/mol的 E值[18], 而另一些学者则得出 E 为196.3~249.9 kJ/mol[19],二者相差4~66倍;同为兖州烟煤,一些学者得到的 E 值为143.65~167.86 kJ/mol[20],而另一些学者则为12.242~56.921 kJ/mol[21],二者相差2~11倍;同为晋东南贫煤,一些学者获得了74.92~248.66 kJ/mol的 E 值[17],而另一些学者则得出 E 为8.522~133.646 kJ/mol[22],二者相差1~8倍.
煤热解是一种极为复杂的固相反应,单一扫描速率法应用于此领域时,其局限性可能会更加突出,并可能会出现新的问题. 本文以准东煤程序升温热解失重数据为研究对象,分析了分段观点和失水脱气阶段失重对计算结果的影响,得到准确且唯一的动力学3因子的可能性以及动力学3因子是否具有明确的理论意义等几个问题,以期进一步提高单一扫描速率法在煤热解领域的实际应用有效性.
1 实验本文所考察的程序升温热解失重数据来自之前研究工作中的R-form煤[26]. 样品的工业和元素分析如表 1所示.
| 表 1 准东原煤样品的工业分析和元素分析[26] |
所用热重系统为瑞士Mettler-Toledo公司的TGA/SDTA851e常压热重分析仪. 每次实验,18 mg左右的样品被盛装在定制的铂金坩埚中,在流量为80 mL·min-1的高纯Ar中被加热至1 000 ℃,采用的升温速率分别为20、40和60 ℃·min-1.
2 动力学分析方法动力学计算采用单一扫描速率法中最具代表性的Coats-Redfern积分法和Achar-Brindley-Sharp-Wendworth微分法,两种方法的具体原理如文献[27-29]所述. 将反应速率基本方程经过变量分离、对数变换、积分近似等一系列数学处理后,得到如下两个等式:
| $\ln \left[ \frac{G\left( \alpha \right)}{{{T}^{2}}} \right]=\ln \left( \frac{AR}{\beta E} \right)-\frac{E}{RT},$ | (1) |
| $\ln \left[ \frac{d\alpha }{f\left( \alpha \right)dT} \right]=\ln \frac{A}{\beta }-\frac{E}{RT}.$ | (2) |
式(1) 为Coats-Redfern积分法方程,式(2) 为Achar-Brindley-Sharp-Wendworth微分法方程. 其中f(α)和G(α)分别为微分形式和积分形式的动力学模式函数,f(α)=1/[dG(α)/dα];α为转化率,$\alpha =\left( {{w}_{0}}-w \right)/\left( {{w}_{0}}-{{w}_{\infty }} \right)$;w0 为样品初始质量(mg), w 为任意时刻样品质量(mg), w∞ 为样品最终质量(mg); T 为任意时刻样品热力学温度,K; β 为升温速率,K/s; R为摩尔气体常数, 8.314 J/(mol·K); E 为表观活化能,J/mol; A 为表观频率因子,s-1. 二者的求解过程相似:将不同的 G(α)和f(α) 分别代入方程(1) 和(2) 后,以 ln[G(α)/T2] 和 ln[dα/(f(α)dT)]对各自的1/T作图,之后以最小二乘法拟合数据,由直线的斜率求得E,截距求得A.
| 表 2 固相反应动力学中常用的模式函数 |
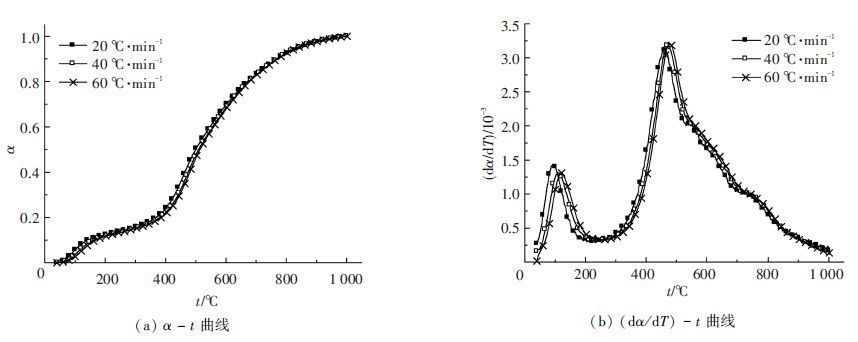
图 1为由不同升温速率下准东原煤热解失重数据计算出的 α-t及(dα/dT)-t曲线,其中t为T所对应的摄氏温度. 需要说明的是,在转化率α的计算中, 样品的初始和最终质量分别定义为程序温度40 ℃和1 000 ℃对应的质量. 由图 1可见, 各α-t及(dα/dT)-t曲线随温升的变化趋势一致, 均呈现4个主要阶段. 以20 ℃·min-1为例进行说明:第1阶段是40~230 ℃,为干燥脱气阶段,主要析出水分和物理吸附的N2和CO2等气体, α-t曲线出现小幅上升后变得平缓,(dα/dT)-t曲线出现小峰(失水峰); 第2阶段是230~350 ℃,为热解初始阶段,煤中高脂肪性的弱键断裂生成小分子气体,同时羧基发生分解析出CO2, α-t和(dα/dT)-t 曲线均较为平缓;第3阶段是350~620 ℃,为主热解阶段,煤基质发生广泛的解聚和分解反应,生成大量以焦油为主的挥发分并形成半焦, α-t曲线急剧上升,(dα/dT)-t 曲线在460 ℃左右出现高峰;第4阶段是620 ℃以上,为2次脱气阶段,主要发生缩聚反应和芳香环小分子侧链的脱落,半焦析出轻气体, α-t和(dα/dT)-t曲线均逐渐变得平缓. 随着升温速率的提高, 上述4个阶段之间的分界温度均向高温方向发生了一定的偏移.
|
图 1 不同升温速率下准东原煤样品热解α-t及(dα/dT)-t曲线 |
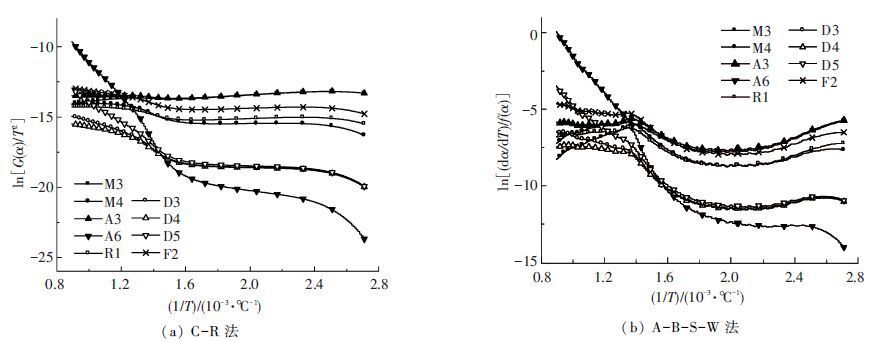
图 2为20 ℃·min-1时,从表 1中选取的9个具有代表性的函数在整个热解温度区间内的Arrhenius曲线,其中 α 的计算范围为0.05-0.95. 由图 2可见,当对热解过程应用C-R积分法和A-B-S-W微分法时,各类模式函数的Arrhenius曲线均呈现明显阶段性,线性相关系数 r 为-0.939 7~0.942 8,总体线性度较低,这表明不能以一组不变的动力学3因子来描述整个温度区间内准东煤的热解失重.
|
图 2 9个具有代表性模式函数的Arrhenius曲线 |
因此,采用单一扫描速率法研究煤热解动力学时一般均需将整个温度范围的失重数据做分段处理[12-25],在每段上分别求取动力学3因子,而这就引出了实际应用中的以下几个问题:
1) 在分段方面的不同观点对动力学计算结果有何影响?
2) 能否获得准确且唯一的动力学3因子?
3) 动力学3因子是否具有明确的理论意义?
下面的内容将针对这几个问题进行逐一探讨.
3.2 在分段方面的不同观点对动力学计算结果的影响目前以单一扫描速率法研究煤热解动力学时,在分段方面主要有以下两种观点:
1) 将整个温度范围内的失重视为一个过程,各阶段的失重视为其接续进行的子过程, 样品初始温度T0对应的α为0,最终温度T∞对应的α为1,各阶段的α取值范围均为[0,1]的子区间,且首尾相接[14-15],此可称为连续转化率观点.
2) 将各阶段失重视为独立过程, 每一阶段均具有独立的T0和T∞且α的取值范围均为[0,1],彼此之间互不影响[16, 19],此可称为独立转化率观点.
然而关于两种观点对动力学计算结果影响的报导还很鲜见.
本文分别以上述两种观点对20 ℃·min-1准东原煤热解失重数据进行划分:
连续转化率观点——以Arrhenius曲线的斜率变化为依据分为4段,第1段为40~140 ℃;第2段为140~360 ℃;第3段为360~600 ℃;第4段为600~1 000 ℃;
独立转化率观点—— 以α-t及(dα/dT)-t 曲线的趋势变化为依据分为3段,第1段为40~230 ℃;第2段为230~620 ℃;第3段为620~1 000 ℃.
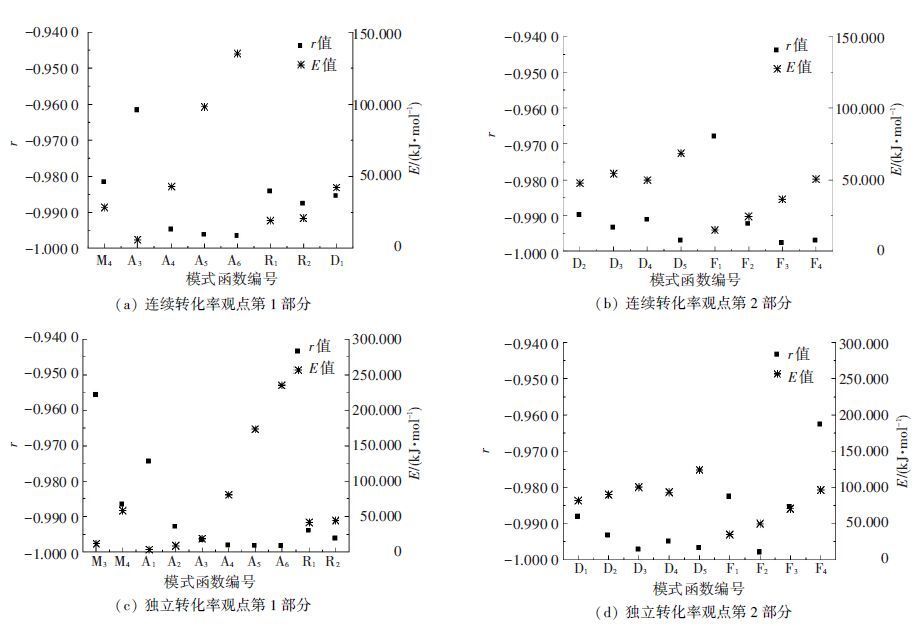
对于煤热解,最主要的考察对象是主热解阶段的动力学参数. 本文分别选取连续转化率观点的第3段和独立转化率观点的第2段作为主热解阶段,以C-R积分法计算二者表观活化能. 需要指出的是,对于连续转化率观点,由于各阶段之间过渡区域的存在,在计算中舍去了区间前端的一小段温度; 对于独立转化率观点,α的计算范围为0.05~0.95. 在二者的计算过程中,均出现了若干种模式函数G(α)均可与实验数据进行良好匹配的情况,图 3显示了r<-0.900 0的模式函数及其对应的r和E值.
|
图 3 在分段方面的不同观点得到的主热解阶段r和E值 |
由图 3可知,不同的分段观点对主热解阶段的动力学计算产生了显著影响,这种影响分为两个方面:1) 达到高匹配度的模式函数的变化;2) 得到的Arrhenius参数的变化. 当采用连续转化率观点时,以 r 值为标准,A5、A6、D5、F3和F4均可与实验数据达到较高匹配程度且彼此之间的匹配度差异不大,它们各自的 r 值分别为-0.996 4、-0.996 7、-0.997 2、-0.997 7和-0.997 2,对应的 E 值为98.259、135.194、68.797、36.386和50.626 kJ/mol. 当采用独立转化率观点时,A4、A5、A6、D3、D5和F2也出现了类似情况,它们各自的 r 值分别为-0.998 2、-0.998 4、-0.998 4、-0.997 3、-0.996 7和-0.998 0,对应的 E 值为80.756、173.407、235.174、100.439、124.201和49.872 kJ/mol. A5、A6、D5可同时与两种分段观点下的实验数据达到高匹配度,但在连续转化率观点下的 E 值均明显低于独立转化率观点. 因此,当采用单一扫描速率法研究准东煤的热解动力学时,明确采用的分段观点对其计算结果的有效评价和比较是十分必要的.
此外,煤的整个热解过程包含了一个最初的失水脱气阶段,大多数学者认为这是一个物理过程,与煤热解的主要机理——化学反应具有本质上的区别,因此在动力学计算时将此阶段的失重予以忽略,即将此阶段之后的某一温度作为样品的初始温度 T0[14-16]; 而另外一些学者则认为此阶段是煤整个热解过程的组成部分,其产生的失重应该计入总失重,因此在动力学计算时予以考虑[23-25].
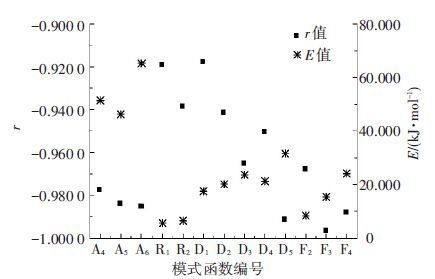
显然,在独立转化率观点下,是否考虑失水脱气阶段的失重对于其他阶段的动力学计算没有影响;而在连续转化率观点下情况则不一样,但关于这一点的讨论在相关文献中还很少见. 本文定义20 ℃·min-1时40~230 ℃为失水脱气阶段. 在连续转化率观点下,仍然选取主热解阶段C-R积分法计算中 r< -0.900 0的模式函数,其考虑和不考虑失水脱气阶段时得到的 r和E 值分别如图 3(a)和4所示. 值得注意的是,在排除此阶段的失重后,一些模式函数可以对主热解和二次脱气阶段总体进行良好的匹配,即在连续转化率观点下,考虑失水脱气阶段与否将会对其他阶段的划分产生直接影响,因此图 4的计算结果也包含了二次脱气阶段.
|
图 4 不考虑失水脱气阶段的主热解和二次脱气阶段总r和E值 |
由图 3(a)和图 4的对比可以看出,D5、F3、F4能够同时与考虑和不考虑失水脱气阶段的实验数据匹配良好且彼此之间的匹配度差异很小. 对于前者,它们各自的 r 值分别为-0.997 2、-0.997 7和-0.997 2,对应的 E 值为68.797、36.386和50.626 kJ/mol;对于后者, r 值分别为-0.991 4、-0.996 7和-0.988 1,对应的 E 值为31.582、15.413和24.136 kJ/mol. 由此可见,排除失水脱气阶段的失重不仅能够影响其他阶段的区域划分,还将使得到的 E 值降低. 因此,对于此种情况下准东煤热解动力学参数的正确评价和比较,明确是否排除了失水脱气阶段的失重是十分必要的.
3.3 获得准确且唯一的动力学3因子的可能性讨论目前,对单一扫描速率法得到的动力学三因子准确程度评价的主要标准是统计学上的线性相关系数 r,|r|越接近1,则认为所选取的模式函数G(α)或f(α)越接近实际, 得到的Arrhenius参数越准确. 然而,由前面的研究结果可知,当对准东煤的热解过程进行分段处理后,单独应用积分法或微分法时会出现多个模式函数均可与实验数据进行准确匹配,且得到的动力学参数差异很大的现象,这就为准东煤热解动力学参数的正确评价和比较带来了困难. 上述现象可简称为多匹配局限性. 为了克服此局限性而获得准确且唯一的动力学3因子,一些学者进行了相关研究. Bagchi等[30]提出采用积分和微分法相结合的方法确定反应模式函数;Criado等[31]提出使用C-R积分方程与A-B-S-W微分方程相结合的方法来筛选出正确的模式函数;另一些文献[4, 32]推荐在几个不同的升温速率下分别对失重数据进行匹配来获得准确的模式函数. 本文将对准东煤的主热解阶段失重数据同时应用C-R积分方程与A-B-S-W微分方程相结合和在3个不同升温速率下分别匹配这两种方法,以验证它们的有效性. 本文定义当C-R法和A-B-S-W法得到的 r 值均小于-0.985 0且相应的 E 值之间的相对误差不超过10%的 G(α)或f(α) 为准确的模式函数.
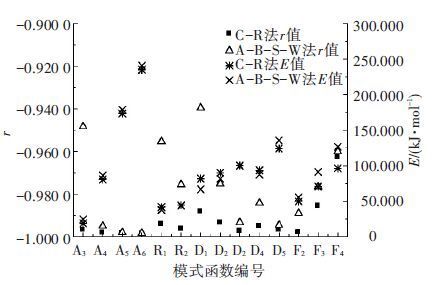
图 5为分别以C-R法和A-B-S-W法对独立转化率分段观点20 ℃·min-1主热解阶段失重数据进行处理, r 均小于-0.900 0的模式函数所对应的 r和E值. 由图 5可见,采用积分和微分法相结合的方式对于筛选出正确的模式函数具有一定帮助,一些在单独应用积分法时匹配度很高的模式函数,在应用微分法时匹配度下降而被排除. 然而,这仍然不足以获得准确且唯一的模式函数. 对于A4、A5、A6、D3和D5,其积分法 r 值分别为-0.998 2、-0.998 4、-0.998 4、-0.997 3和-0.996 7,相应的微分法 r 值为-0.995 0、-0.998 0、-0.998 3、-0.993 3和-0.994 5,均达到很高的匹配度;对应的 E 值相对误差分别为6.61%、3.19%、2.37%、0.56%和8.35%. 因此它们都是足够准确的模式函数,但不难发现它们彼此的 E 值差异很大.
|
图 5 主热解阶段C-R法及A-B-S-W法r<-0.900 0模型函数的r和E值 |
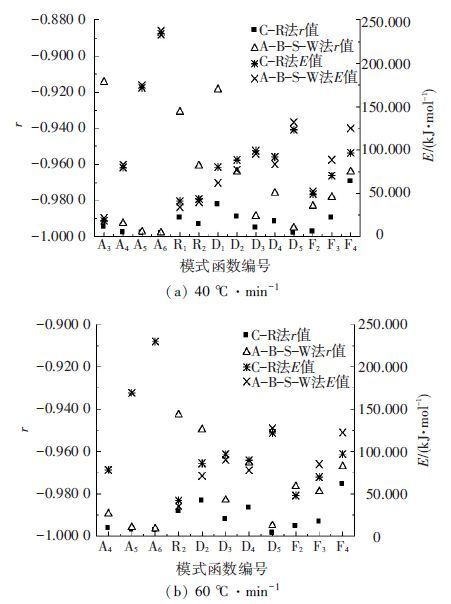
图 6为分别以C-R法和A-B-S-W法对独立转化率分段观点40和60 ℃·min-1主热解阶段失重数据进行处理, r均小于-0.900 0的模式函数所对应的r和E值. 由图 6(a)可知,在40 ℃·min-1升温速率下,准确的模式函数为A4、A5、A6、D3和D5,其积分法 r 值分别为-0.997 9、-0.998 2、-0.998 3、-0.995 3和-0.998 0,对应的微分法 r 值为-0.992 5、-0.997 3、-0.997 9、-0.988 7和-0.995 1;相应的 E 值相对误差为3.64%、1.72%、1.27%、3.45%和6.61%. 由图 6(b)可知,在60 ℃·min-1升温速率下,准确的模式函数为A4、A5、A6和D5,其积分法 r 值分别为-0.996 3、-0.997 1、-0.997 2和-0.998 4,对应的微分法 r 值为-0.989 4、-0.995 7、-0.996 5和-0.995 0;相应的 E 值相对误差为0.07%、0.03%、0.02%和4.54%. 此外,A4、A5、A6和D5的 E 值随升温速率的变化均很小. 由此可见,通过积分和微分法相结合与3个不同升温速率下分别匹配这两种方法的同时运用,仍然存在4个模式函数A4、A5、A6和D5能够与实验数据匹配良好,但相应的 E 值差异很大,因此无法获得准确且唯一的动力学参数.
|
图 6 40 ℃·min-1和60 ℃·min-1下主热解阶段C-R法及A-B-S-W法r<-0.900 0模型函数的r和E值 |
造成单一扫描速率法的多匹配局限性的根本原因是,其反应速率基本方程是由等温单步反应速率方程演化而来,而等温单步反应的基本假设是与实际非等温固相反应的复杂多步本质相悖的. 由反应速率方程可知,过程速率是T和α的函数,其对T的依赖性由速率常数k(T) 即Arrhenius方程体现, 而对α的依赖性则由模式函数f(α)体现. 将非等温数据以假定的模式函数f(α)进行匹配时, Arrhenius参数由假定的 f(α)的形式所决定. 在非等温实验中, T和α同时变化,而单一扫描速率法不能将k(T)和f(α)进行有效地分离,因此只能同时而不是分步地求解动力学3因子,这样就导致了若干G(α)或f(α) 均可以通过以Arrhenius参数强烈变化为代价的方式补偿它们与真实模式函数之间的差异,从而对数据进行在统计学上准确的匹配,进而得到高度分散的Arrhenius参数. 准东煤的热解作为一种包含多种反应路径的复杂固相反应,在对其非等温实验数据进行模式匹配时,此种补偿效应尤为显著,以至于同时运用积分和微分法相结合与在3个不同升温速率下分别匹配这两种被认为在一般非等温固相反应中可以通过增加额外的限制而有效削弱补偿效应的方法,也不能获得准确且唯一的动力学3因子. 因此,当采用单一扫描速率法研究准东煤的热解动力学时,明确选用的模式函数对于动力学参数的正确评价和比较是十分必要的.
3.4 动力学3因子理论意义的探讨反应模式函数可以确定反应机理,同时相应的Arrhenius参数可以由过渡态理论进行合理地诠释,是人们对于单一扫描速率法的最重要期望之一. 然而本文的研究结果表明,这种期望对于准东煤热解的动力学研究是不切实际的.
首先,这种期望是源于等温单步反应动力学的基本假设,而这是与准东煤热解的实际过程相悖的. 准东煤热解是一个包括了桥键断裂、交联、氢传输、取代、缩聚等极为复杂的反应体系,除此之外,其还耦合了传热和传质等物理过程. 转化率 α 以总失重量的分数来表征过程的总包转化程度,因此其包含了以上全部过程的影响. 通过以 α 为自变量的模式函数在统计学上的匹配求得的表观Arrhenius参数,应该是各独立基元反应的Arrhenius参数、额外的物理过程的等效Arrhenius参数、以及各基元反应和物理过程的相对贡献度的复杂函数. 随着 α和T的变化, 各基元反应及物理过程对表观转化速率的贡献度将发生变化,表观Arrhenius参数和过程控制机理将改变,而单一扫描速率法获得的表观Arrhenius参数和模式函数在某个区间内是不变的,这样的动力学参数仅仅是对某个阶段样品表观失重行为的总体近似描述,而对揭示过程的反应机理帮助甚微. 此外,由前面的研究结果可知,往往几个模式函数可以同时完成对实验数据的良好匹配,但彼此之间的 E 值差异很大,说明以统计学标准看,能够准确描述实验数据的动力学三因子并非唯一,进一步表明它们的作用仅仅是再现实验数据,而其物理意义是模糊不清的.
其次,“模式函数匹配”这种方法本身存在一定的局限性. 因为每一个“准确的”模式函数,均是从一个由有限个备选函数人为组建的列表中筛选出来,而在此之前无法确定列表中是否已经包含了那个最接近实际的“最佳匹配”模式函数. 换言之,由此得到的“准确的”模式函数,永远只是相对于列表中的其他函数而言,并非绝对意义上的“准确”.
第三,各类模式函数本身对于实际固相反应的描述具有一定局限性. 目前,使用的模式函数绝大多数采用了反应物颗粒具有规整的几何形状和各向同性的反应活性的基本假设[33],此外为了简化计算还可能附加一些特殊假设,然而随着现代物理化学测试技术的飞速发展,一些实验数据已经证明这些假设对于某些固相反应并不适用. 例如Mampel的关于分解反应物的每个颗粒只产生一个核的假设,在今天电子显微镜得到的证据看来是不切实际的[4];Jander三维扩散模式假设具有规整立方体或球状的样品颗粒的反应界面沿着三维方向由外向内各向同性地等速推进,但是近年来用扫描电子显微镜技术对一些金属盐类的分解和脱水过程进行直接观察的结果证明实际情况并非如此[34-35]. 准东煤是一种结构复杂的非匀质固相反应物,热重实验中其颗粒的几何形状并非规整,堆积状况也非规则,这些因素均会使其失重行为偏离各类模式函数的描述.
最后,甚至一些模式函数本身与反应机理之间的对应关系也很模糊. Dollimore[36]指出几种完全不同的机理可以生成同一个模式函数以及同一种机理能够产生几种模式函数;实际上,本文表 3中的A类和F类模式函数在某些情况下是相似的,例如当二者的 n 均为1时,它们具有相同的数学形式,然而却具有不同的物理意义.
综上所述,由于准东煤热解的复杂多步本质以及模式函数匹配法本身的局限性,由单一扫描速率法得到的动力学3因子的理论意义是十分模糊的,很难将模式函数与过程机理相联系,也很难将Arrhenius参数作为过程的固有特征而与能量壁垒或活化络合物的振动频率等过渡态理论中的概念相联系. 因此,在使用它们解释热重实验过程中准东煤热解的控制机理时要十分谨慎.
4 结论1) 对于准东煤的热解,在分段方面的不同观点对高匹配度模式函数的类别及Arrhenius参数均具有显著影响,连续转化率观点下得到的表观活化能 E 明显低于独立转化率观点.
2) 当采用连续转化率观点时,排除失水脱气阶段的失重不仅能够影响其他阶段的区间划分,还将使得到的 E 值降低.
3) 同时运用积分和微分法相结合与在3个不同升温速率下分别匹配这两种方法,也不能获得准确且唯一的动力学3因子,因此动力学3因子的理论意义是有限的.
4) 阐明失重数据的预处理方法和模式函数的选择,对于动力学参数的评价和交流是十分必要的,同时以动力学3因子解释热解机理时要十分谨慎.
致谢: 感谢国家自然科学基金项目《我国低阶煤煤焦低温气化反应性的研究》(批准号51376053) 和国家自然科学基金委创新研究群体项目《热辐射传输与流动控制》(批准号51421063) 对本文研究工作的支持.| [1] |
VYAZOVKIN S, WIGHT C A. Model-free and model-fitting approaches to kinetic analysis of isothermal and nonisothermal data[J].
Thermochimica Acta,1999, 340 : 53-68.
( 0) 0)
|
| [2] |
OPFERMANN J R, KAISERSBERGER E, FLAMMERSHEIM H J. Model-free analysis of thermoanalytical data-advantages and limitations[J].
Thermochimica Acta,2002, 391 (1) : 119-127.
( 0) 0)
|
| [3] |
BROWN M E, MACIEJEWSKI M, VYAZOVKIN S, et al. Computational aspects of kinetic analysis: part A: the ICTAC kinetics project-data, methods and results[J].
Thermochimica Acta,2000, 355 (1) : 125-143.
( 0) 0)
|
| [4] |
MACIEJEWSKI M. Computational aspects of kinetic analysis: part B: The ICTAC kinetics project—the decomposition kinetics of calcium carbonate revisited, or some tips on survival in the kinetic minefield[J].
Thermochimica Acta,2000, 355 (1) : 145-154.
( 0) 0)
|
| [5] |
VYAZOVKIN S. Computational aspects of kinetic analysis: part C: The ICTAC kinetics project—the light at the end of the tunnel?[J].
Thermochimica Acta,2000, 355 (1) : 155-163.
( 0) 0)
|
| [6] |
BURNHAM A K. Computational aspects of kinetic analysis: part D: The ICTAC kinetics project—multi-thermal-history model-fitting methods and their relation to isoconversional methods[J].
Thermochimica Acta,2000, 355 (1) : 165-170.
( 0) 0)
|
| [7] |
RODUIT B. Computational aspects of kinetic analysis: part E: The ICTAC kinetics project—numerical techniques and kinetics of solid state processes[J].
Thermochimica Acta,2000, 355 (1) : 171-180.
( 0) 0)
|
| [8] |
BUDRUGEAC P, SEGAL E. Some methodological problems concerning nonisothermal kinetic analysis of heterogeneous solid-gas reactions[J].
International Journal of Chemical Kinetics,2001, 33 (10) : 564-573.
( 0) 0)
|
| [9] |
MUŞAT V, BUDRUGEAC P, MONTEIRO R C C, et al. Non-isothermal kinetic study on the decomposition of Zn acetate-based Sol-gel precursor. Part Ⅰ. Application of the isoconversional methods[J].
Journal of thermal analysis and calorimetry,2007, 89 (2) : 505-509.
( 0) 0)
|
| [10] |
BUDRUGEAC P, MUŞAT V, SEGAL E. Non-isothermal kinetic study on the decomposition of Zn acetate-based sol-gel precursor. part II. The application of the IKP method[J].
Journal of thermal analysis and calorimetry,2007, 88 (3) : 699-702.
( 0) 0)
|
| [11] |
MARCILLA A, GARCIA-QUESADA J C, RUIZ-FEMENIA R. Additional considerations to the paper entitled: Computational aspects of kinetic analysis. part B: The ICTAC kinetics project—the decomposition kinetics of calcium carbonate revisited, or some tips on survival in the kinetic minefield.[J].
Thermochimica acta,2006, 445 (1) : 92-96.
( 0) 0)
|
| [12] |
CEYLAN K, KARACA H, ÖNAL Y. Thermogravimetric analysis of pretreated Turkish lignites[J].
Fuel,1999, 78 (9) : 1109-1116.
( 0) 0)
|
| [13] |
LU Yongkang, CHANG Liping, XIE Kechang. Effects of coal structure on its pyrolysis characteristics under N2 and Ar atmosphere[J].
Energy Sources,2001, 23 (8) : 717-725.
( 0) 0)
|
| [14] |
ARENILLAS A, RUBIERA F, PEVIDA C, et al. A comparison of different methods for predicting coal devolatilisation kinetics[J].
Journal of Analytical and Applied Pyrolysis,2001, 58-59 : 685-701.
( 0) 0)
|
| [15] |
GÜNEŞ M, GÜNEŞ S. A study on thermal decomposition kinetics of some Turkish coals[J].
Energy Sources,2005, 27 (8) : 749-759.
( 0) 0)
|
| [16] |
LIU Quanrun, HU Haoquan, ZHOU Qiang, et al. Effect of inorganic matter on reactivity and kinetics of coal pyrolysis[J].
Fuel,2004, 83 : 713-718.
( 0) 0)
|
| [17] |
何佳佳. 反应条件对煤挥发分析出过程影响的TG-FTIR分析[D]. 哈尔滨: 哈尔滨工业大学, 2007: 54-55.
( 0) 0)
|
| [18] |
降文萍. 煤热解动力学及其挥发分析出规律的研究[D]. 太原: 太原理工大学, 2004: 59-62.
( 0) 0)
|
| [19] |
吴波. 神东和平朔煤在不同反应器中的热解特性[D]. 大连: 大连理工大学, 2009: 42-43.
( 0) 0)
|
| [20] |
王俊琪, 方梦祥, 骆仲泱, 等. 煤的快速热解动力学研究[J].
中国电机工程学报,2007, 17 : 18-22.
( 0) 0)
|
| [21] |
张妮, 曾凡桂, 降文萍. 中国典型动力煤种热解动力学分析[J].
太原理工大学学报,2005 (5) : 549-552.
( 0) 0)
|
| [22] |
曾光. 我国典型低挥发分煤热解成分的定量分析[D]. 哈尔滨: 哈尔滨工业大学, 2008: 44-45.
( 0) 0)
|
| [23] |
李爽, 杨斌, 冯秀燕, 等. 典型陕北长焰煤热解行为及其动力学实验研究[J].
大连理工大学学报,2013, 53 (3) : 333-339.
( 0) 0)
|
| [24] |
宋绍勇. 煤热解动力学及其机理的实验研究[D]. 太原: 太原理工大学, 2002: 34-39.
( 0) 0)
|
| [25] |
陈燕. 东乌旗煤及不同化学组分热解动力学及其挥发分析出规律研究[D]. 太原: 太原理工大学, 2011: 43-44.
( 0) 0)
|
| [26] |
邱朋华, 赵岩, 陈希叶, 等. 碱及碱土金属对准东煤热解特性及动力学影响分析[J].
燃料化学学报,2014, 10 : 1178-1189.
( 0) 0)
|
| [27] |
COATS A W, REDFERN J P. Kinetic parameters from thermogravimetric data[J].
Nature,1964, 201 : 68-69.
( 0) 0)
|
| [28] |
ACHAR B N N, BRINDLEY G W, SHARP J H. Kinetics and mechanism of dehydroxylation processes. III. Applications and limitations of dynamic methods[C]//Proc Int Clay Conf. Jerusalem: Israel University Press, 1966: 67-70.
( 0) 0)
|
| [29] |
SHARP J H, WENTWORTH S A. Kinetic analysis of thermogravimetric data[J].
Analytical chemistry,1969, 41 (14) : 2060-2062.
( 0) 0)
|
| [30] |
BAGCHI T P, SEN P K. Combined differential and integral method for analysis of non-isothermal kinetic data[J].
Thermochimica Acta,1981, 51 (2) : 175-189.
( 0) 0)
|
| [31] |
CRIADO J M, ORTEGA A. Remarks on the discrimination of the kinetics of solid-state reactions from a single non-isothermal trace[J].
Journal of thermal analysis,1984, 29 (6) : 1225-1236.
( 0) 0)
|
| [32] |
CABALLERO J A, CONESA J A. Mathematical considerations for nonisothermal kinetics in thermal decomposition[J].
Journal of analytical and applied pyrolysis,2005, 73 (1) : 85-100.
( 0) 0)
|
| [33] |
胡荣祖, 高胜利, 赵凤起, 等.
热分析动力学[M]. 北京: 科学出版社, 2008 : 4 -6.
( 0) 0)
|
| [34] |
TANAKA H. Thermal analysis and kinetics of solid state reactions[J].
Thermochimica Acta,1995, 267 : 29-44.
( 0) 0)
|
| [35] |
KOGA N, TANAKA H. Effect of sample mass on the kinetics of thermal decomposition of a solid. Part 3. Non-isothermal mass-loss process of molten NH4NO3[J].
Thermochimica Acta,1994, 240 : 141-151.
( 0) 0)
|
| [36] |
DOLLIMORE D. The application of thermal analysis in studying the thermal decomposition of solids[J].
Thermochimica Acta,1992, 203 : 7-23.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


