圆锥曲线在几何学中是个值得研究深入的课题,与圆锥轴线成不同角度的平面截切圆锥会得到圆、椭圆[1]、抛物线[2]、双曲线、三角形5种类型的交线[3],并称为圆锥曲线,王书营[4]研究得出圆锥曲线的性质有着对立统一的关系. 田福润等[5]研究了一般位置平面截切正圆锥和铅垂面截切斜圆锥,截交线特殊点的两种情况. 圆锥与同轴的回转体相贯线是圆[6]. 而不同轴相贯相交曲线即是二次曲线. 与圆锥同轴圆柱的相贯线是相当于轴线上一定点到圆锥表面成相同角度的动点的轨迹,其轨迹是个圆. 近年来,研究圆锥的热点集中在圆锥与回转体相贯线问题上,如谷艳华等[7]详细研讨了柱锥正贯的相贯线最右点的解析. 清华大学的刘敏等[8]图解分析了柱锥轴线斜交相贯线变化规律和极值点的求解. 孙岩[9]研究了点到定直线和定平面距离比为常数的轨迹问题. 李世臣等[10]利用公式生成法研究了点的轨迹问题. 在控制理论研究中,研究点轨迹问题有图解法和解析法[11],而解析法得出都是代数方程[12]. 理论物理学在研究等离子体介质色散,也有计算磁单极子沿圆锥曲线运动的辐射运动轨迹问题[13]. 天体物理学研究行星按圆锥曲线运动的时间计算中,也会涉及至锥面最短距离的解析[14]. 王泽南[15]利用极坐标方程的虚实部分解的方式,极大简化了计算. 笔者在教学过程中发现了以往书本中所未提及的一个定点投影轨迹问题,某定点不在轴线上而在圆锥内,定点到圆锥表面垂直距离点的轨迹是什么?轨迹交线如何求得,且交线是何种形式,这是个值得研究的问题,以往文献也从未提及.
1 圆锥内定点至圆锥表面垂足点求解圆锥面是由与轴线成锐角的母线绕其旋转一周而形成,母线旋转的任意位置称之为素线. 那么圆锥内一点到圆锥表面距离就相当于由定点A作任意素线的垂线,交点为垂足动点T,如图 1所示.
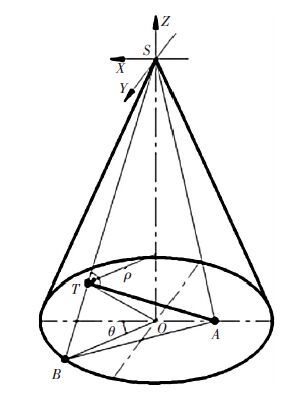
|
图 1 垂点立体解析 |
为便于研究,圆锥内任意点A可以取在圆锥底面上(即使在圆锥内也可以过A作垂直于轴线的截面切掉下半部圆台),以圆锥顶点为坐标原点,圆锥轴线方向为Z轴,同时A点设在平行于X轴的底圆上. 圆锥半顶角为β,底圆周半径为R,圆锥高为h,A距离底圆圆心为a. 于圆锥锥顶S建立直角坐标系,以圆锥任意点T至轴线距离ρ和X轴间角θ为参数的曲面方程为
| ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}_{ST}}\left( \rho ,\theta \right)=\left( \rho \cos \text{ }\theta ,\rho \sin \text{ }\theta ,-\rho \cot \text{ }\beta \right).$ |
A点坐标为(-a,0,-h). B点坐标为(Rcos θ,Rsin θ,-h),S点坐标为(0,0,0) ,O点坐标为(0,0,-h).
因T在SB上,所以设T:
| $\begin{align} & \left( kR\cos \text{ }\theta ,kR\sin \text{ }\theta ,-kh \right),\text{ }0<k<1; \\ & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{A0}}={{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{0}}-{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{A}}=\left( a,0,0 \right), \\ & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{OT}}={{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{T}}-{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{0}}=\left( kR\cos \text{ }\theta ,kR\sin \text{ }\theta ,\left( -k \right)h \right), \\ & {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{AT}}={{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{A0}}+{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{OT}}. \\ \end{align}$ | (1) |
由式(1) 得
| ${{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{AT}}\left( \rho ,\theta \right)=\left( kR\cos \text{ }\theta +a,kR\sin \text{ }\theta ,\left( -k \right)h \right),$ | (2) |
| ${{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}}_{ST}}\left( \rho ,\theta \right)=\left( kR\cos \text{ }\theta ,kR\sin \text{ }\theta ,Kh \right).$ | (3) |
因为${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}$ST⊥${\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r}}$AT,所以式(2) 与式(3) 的点积等于0. 由此可以推导出T点以参数θ、k为坐标的曲线方程.
由式(2) ·(3) =0得
| $k\left( {{R}_{2}}+{{h}_{2}} \right)+aR\cos \theta -{{h}^{2}}=0.$ | (4) |
简化式(4) 得
| $k={{\cos }^{2}}\beta -\left( a/R \right){{\sin }^{2}}\beta \cos \theta .$ | (5) |
由h=Rcot β,则T点坐标为
| $k\left( R\cos \text{ }\theta ,kR\sin \text{ }\theta ,-kR\cot \beta \right),0<k<1.$ | (6) |
将式(5) 代入式(6) ,写成笛卡尔坐标形式:
| $x=\left( {{\cos }^{2}}\beta -\left( a/R \right){{\sin }^{2}}\beta \cos \theta \right)R\cos \text{ }\theta ,$ | (7) |
| $y=\left( {{\cos }^{2}}\beta -\left( a/R \right){{\sin }^{2}}\beta \cos \theta \right)R\sin \text{ }\theta ,$ | (8) |
| $z=-\left( {{\cos }^{2}}\beta -\left( a/R \right){{\sin }^{2}}\beta \cos \theta \right)R\cot \text{ }\beta .$ | (9) |
式(7) ~(9) 中x、y、z值域分别为:
| $\begin{align} & R{{\cos }^{2}}\beta -a{{\sin }^{2}}\beta \le x\le R{{\cos }^{2}}\beta +a{{\sin }^{2}}\beta , \\ & R{{\cos }^{2}}\beta \le y\le -R{{\cos }^{2}}\beta , \\ & -a{{\sin }^{2}}\beta -R{{\cos }^{3}}\beta \sin \beta \le z\le a\sin \beta -R{{\cos }^{3}}\beta \sin \beta . \\ \end{align}$ |
此为关于θ的函数方程,其余参数均为常量,满足锥面直角坐标方程
| ${{x}^{2}}+{{y}^{2}}-{{z}^{2}}{{\tan }^{2}}\beta =0.$ | (10) |
式(7) 除以式(9) 得
| $cos\theta =-\cot \beta \left( x/z \right),$ | (11) |
将式(11) 代入式(9) 得到z与x的关系式
| ${{z}^{2}}+h{{\cos }^{2}}\beta x.$ | (12) |
式(10) 变形得
| ${{z}^{2}}=\left( {{x}^{2}}+{{y}^{2}} \right){{\cot }^{2}}\beta .$ | (13) |
式(13) 代入式(12) 得
| ${{x}^{2}}+{{y}^{2}}+h{{\sin }^{2}}\beta z+a{{\sin }^{2}}\beta x=0.$ | (14) |
式(12) 加式(14) 并简化得:
| $\left\{ \begin{matrix} {{x}^{2}}+{{y}^{2}}+{{z}^{2}}+ax+hz=0, \\ {{\left( x+a/2 \right)}^{2}}+{{y}^{2}}+{{\left( z+h/2 \right)}^{2}}+ax+hz= \\ {{a}^{2}}/4+{{h}^{2}}/4. \\ \end{matrix} \right.$ | (15) |
式(15) 为T点所属另一曲面,是以(-a/2,0,-h/2) 为圆心,圆心到圆锥顶点为半径的球面. 联立式(11) 和式(15) ,得到圆锥内定点至素线垂足点轨迹是以定点与圆锥顶点连线的中点为圆心,定点到圆锥顶点距离为直径的球面与圆锥面相交线,如图 2所示.

|
图 2 垂足轨迹交线 |
| $\left\{ \begin{matrix} {{x}^{2}}+{{y}^{2}}-{{z}^{2}}=t, \\ {{\left( x+a/2 \right)}^{2}}+{{y}^{2}}+{{\left( z+h/2 \right)}^{2}}=\left( {{a}^{2}}/4+{{h}^{2}}/4 \right). \\ \end{matrix} \right.$ | (16) |
由式(12) 得
| $\left\{ \begin{matrix} {{z}^{2}}+h{{\cos }^{2}}\beta z=-a{{\cos }^{2}}\beta x, \\ y=0. \\ \end{matrix} \right.$ |
此方程组为曲线的正面投影,则
| ${{\left( z+h{{\cos }^{2}}\beta /2 \right)}^{2}}=-a{{\cos }^{2}}\beta x+{{h}^{2}}{{\cos }^{4}}\beta /4.$ |
此正面投影是以(h2cos2β/4a,-hcos2β/2) 为顶点,以(h2cos2β/4a-acos2β/2,-hcos2β/2) 为焦点,开口朝Z轴正向的抛物线的一段. 截交线投影图如图 3所示,由图 3可以看出这段抛物线与直线很贴近. 当a=0时,就是z=-hcos2β的平行X轴的直线段.
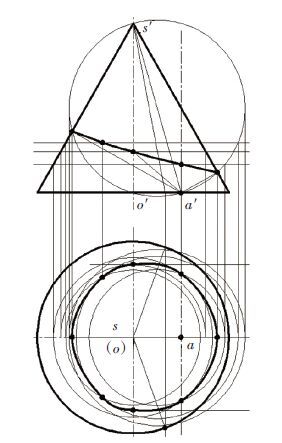
|
图 3 垂足轨迹投影 |
由联立的式(16) ,消去z,并与z=0联立得到水平投影方程式.
| $\left\{ \begin{array}{*{35}{l}} {{x}^{2}}+{{y}^{2}}+a{{\sin }^{2}}\beta x+R{{\cos }^{2}}\beta \sqrt{{{x}^{2}}+{{y}^{2}}}=0, \\ Z=0. \\ \end{array} \right.$ |
水平投影为一封闭的二次曲线,曲线和椭圆很近似. 当a=0时,就是一个半径为Rcos2β,圆锥顶点在圆锥底面投影为圆心的圆.
4 结论1) 从圆锥内一点作素线垂线,所有垂足点的轨迹是以定点与圆锥顶点为直径的圆球与圆锥的交线.
2) 过圆心与圆内任意点连线为直径做球面,球面与某素线交点与任意点连线垂直素线.
3) 圆锥斜贯圆球相贯线为二次曲线,其正面投影为抛物线.
| [1] |
赵炳利, 伍友新, 贾春玉, 等. 平面相交圆锥为椭圆时的投影分析[J].
燕山大学学报,1998, 35 (3) : 263-265.
( 0) 0)
|
| [2] |
王凤春. 圆锥曲线史话[J].
数学通报,2010, 63 (9) : 60-62.
( 0) 0)
|
| [3] |
杨绪利. 圆锥截交线的形状分析及几何证明[J].
农机化研究,2005 (5) : 76-78.
( 0) 0)
|
| [4] |
王书营. 圆锥截线的一致性分析[J].
南京工业职技学院学报,2012, 12 (4) : 52-56.
( 0) 0)
|
| [5] |
田福润, 陈光, 刘玉洁. 圆锥截交线上特殊点的求法[J].
长春工业大学学报(自然科学版),2011, 32 (5) : 507-509.
( 0) 0)
|
| [6] |
袭建军, 王熙宁, 李利群, 等.
画法几何及机械制图[M]. 哈尔滨: 黑龙江人民出版社, 2009 : 129 -130.
( 0) 0)
|
| [7] |
谷艳华, 侯洪生, 张秀芝. 圆柱与圆锥轴线相交时左侧相贯线上最右点的解析证明与图解[J].
工程图学学报,2010 (4) : 146-150.
( 0) 0)
|
| [8] |
刘敏, 林犀, 陈涓. 柱锥斜交相贯线解析性质分析与特殊点图解方法[J].
图学学报,2014, 35 : 682-689.
( 0) 0)
|
| [9] |
孙岩. R2,1中二次曲面的化简与点的轨迹方程[J].
鞍山科技大学学报(自然科学版),2005, 28 (2) : 92-95.
( 0) 0)
|
| [10] |
李世臣, 王劲松. 一类轨迹方程的公式生成法[J].
数学通讯,2012 (2) : 41-43.
( 0) 0)
|
| [11] |
周立峰.
根轨迹法极其在自动控制中的应用[M]. 成都: 四川科学技术出版社, 1985 : 12 -13.
( 0) 0)
|
| [12] |
王泽南. 建立根轨迹代数方程的一种新方法[J].
安徽工学院学报,1993, 12 (1) : 37-45.
( 0) 0)
|
| [13] |
张文东.沿圆锥曲线运动辐射和调制不稳定性的研究[D].南昌:南昌大学,2007: 16-20.
( 0) 0)
|
| [14] |
蔡志东. 物体作圆锥曲线运动的时间计算[J].
山东理工大学学报(自然科学版),2010, 24 (2) : 16-19.
( 0) 0)
|
| [15] |
王泽南. 一种简易的根轨迹方程—极坐标方程的建立[J].
天津大学学报(自然科学版),2002, 35 (1) : 75-77.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


