2. 哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001
2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
热障涂层(thermal barrier coating,TBC)活塞有助于改善内燃机的燃烧性能、排放性能、抗爆震性能等,TBC最重要的作用是为活塞基体提供热防护,减少传入活塞基体的热量. 而TBC应当采用何种形式,以及TBC对于活塞热力性能的改变是设计阶段需要研究的重要问题.
建立适用于热障涂层活塞热力性能研究的数值方法,作为TBC活塞设计阶段的预测工具,分析TBC活塞温度场、热应力场、热变形具有重要意义.
目前,关于TBC活塞热力性能的数值仿真相对较少,一般采用的是基于FEM的商用软件.王素等[1-3]采用ADINA数值分析复合材料活塞的整体性能,指出使用陶瓷纤维梯度层可以明显改变活塞温度分布,缓和由于热膨胀系数不匹配,在陶瓷纤维增强层与活塞本体交界处产生的应力,但没有详细讨论活塞表面热应力性能.Buyukkaya等[4-5]在活塞上表面全部涂覆TBC,采用ANSYS数值模拟其温度场,指出普通活塞的最大温度出现在燃烧室中心,而TBC活塞的最大温度在燃烧室与活塞顶面交界处.Cerit等[6-7]在活塞顶面局部涂覆TBC,采用ANSYS数值模拟其温度场及热应力场,给出了温度、应力在各材料交界面处的分布曲线.由于TBC活塞在基体表面有涂层材料,相对于传统活塞数值分析,TBC活塞数值分析需要额外考虑如何划分TBC区域网格和如何处理非均匀材料.Aboudi等[8]指出,为了获得正确的复合材料热应力场,在控制方程的离散过程中需要引入物性参数的空间变化.传统的FEM赋予每一个网格单元均匀的物性参数,未考虑材料属性的空间变化,这一处理可能导致计算结果存在人工数值不连续问题[9-11].
龚京风等[12-15]发展了一种适用于二维复合材料热应力研究的格点型有限体积方法(cell vertex FVM,CV-FVM),数值结果表明,CV-FVM能够有效避免物性参数引起的数值不连续问题.本文进一步将CV-FVM推广应用于三维问题,通过数值算例验证计算方法的正确性,并基于CV-FVM分析TBC活塞热力性能.
1 基本方程考虑稳态情况下各向同性线弹性复合材料的热应力问题,材料的物性参数随空间变化.基于控制体Ω建立热传导和热弹性方程,Ω体积为V,边界面为S.
1.1 热传导方程热传导控制方程为
| $\int{_{V}\rho c\frac{\partial T}{\partial t}}\text{d}V=\oint{_{s}}k\frac{\partial T}{\partial x}{{n}_{\alpha }}\text{d}S+\int{_{V}{{q}_{VT}}\text{d}V.}$ | (1) |
式中:ρ、c、T、k分别为密度、比热容、温度、热传导系数; nα为微元边界S的单位外法线矢量分量,α=x,y,z; qVT为热源在单位时间单位体积内产生的热量,本文不涉及热源,后文中将省略相应内容.考虑3种边界条件:
| $T={{T}_{B}},边界{{S}_{D}},$ | (2) |
| $-k\frac{\partial T}{\partial {{x}_{\alpha }}}{{n}_{\alpha }}={{q}_{B}},边界{{S}_{N}},$ | (3) |
| $-k\frac{\partial T}{\partial {{x}_{\alpha }}}{{n}_{\alpha }}={{h}_{B}}\left( T-{{T}_{\infty }} \right),边界{{S}_{R}}.$ | (4) |
式中:TB为Dirichlet边界SD上给定的温度;qB为Neumann边界SN上给定的法向热流量;hB为Robin边界SR上给定的对流换热系数,T∞为环境温度.下标B代表边界.
1.2 热弹性方程热弹性控制方程为
| $\int{_{V}\rho c\frac{{{\partial }^{2}}{{u}_{\alpha }}}{\partial {{t}^{2}}}}\text{d}V=\oint{_{s}}{{\sigma }_{\alpha \beta }}{{n}_{\beta }}\text{dS+}\int{_{V}\rho {{f}_{\alpha }}}\text{d}V.$ |
式中: uα为位移矢量的分量,σαβ为应力张量的分量,fα为体积力矢量的分量.本文不涉及体积力,后文中将省略相应内容.
利用线弹性体的本构方程及几何方程,热弹性方程可写为
| $\begin{align} & \int{_{V}\rho c\frac{{{\partial }^{2}}{{u}_{\alpha }}}{\partial {{t}^{2}}}}\text{d}V=\oint{_{s}}\left[ G\left( \frac{\partial {{u}_{\alpha }}}{\partial {{x}_{\beta }}}+\frac{\partial {{u}_{\beta }}}{\partial {{x}_{\alpha }}} \right){{n}_{\beta }}+\lambda \left( \frac{\partial {{u}_{\lambda }}}{\partial {{x}_{\lambda }}} \right){{\delta }_{\alpha \beta }}{{n}_{\beta }} \right]\text{dS}- \\ & \oint{_{s}}\Gamma a\left( T-{{T}_{r}} \right){{\delta }_{\alpha \beta }}{{n}_{\beta }}\text{dS}. \\ \end{align}$ | (5) |
式中: Γ为热弹性系数; G、λ为拉姆系数; a为线膨胀系数;Tr为参考温度,当T=Tr时结构的热应变为0;δαβ为克罗尼克尔符号,当α=β时δαβ=1,当α ≠ β时δαβ=0.
考虑边界条件:
| $\begin{align} & {{u}_{\alpha }}={{u}_{\alpha B}},边界{{S}_{\text{D}}}, \\ & {{\sigma }_{\alpha \beta }}{{n}_{\beta }}={{\sigma }_{n\text{B}}},边界{{S}_{\text{N}}}. \\ \end{align}$ | (6) |
式中: uαB为边界SD上给定的位移;σnB为边界SN上给定的法向应力.
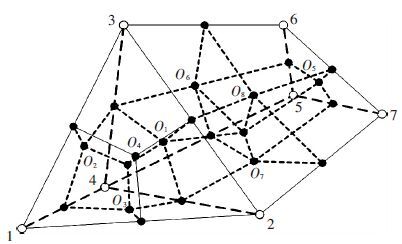
2 数值离散对于本文考虑的活塞热应力问题,数值方法应能够处理三维非结构化网格.围绕网格节点依次连接相邻单元中心和面中心建立控制体,见图 1.空心圆点代表网格节点,实心圆点代表体中心及面中心.用粗实线及虚线围成网格,细实线及点划线围成控制体.关于二维问题的数值离散参考文献[12-15].
本文采用交错网格技术模拟TBC活塞物性参数的空间变化.在网格节点上定义待解变量(温度和位移),并假设在控制体内均匀分布;将已知量(如物性参数)定义在单元中心,并假设在网格单元内均匀分布.考虑控制体与网格单元的关系,可知控制体内物性参数是变化的,从而在离散过程中考虑空间变化的物性参数.
|
图 1 三维网格示意 |
利用向后差分格式离散热传导方程(1) 左端的一阶时间项,得
| $\int{_{V}\rho c\frac{\partial T}{\partial t}}\text{d}V=\left( \sum\limits_{i=1}^{{{n}_{c}}}{\frac{{{\rho }_{i}}{{c}_{i}}{{V}_{i}}}{{{n}_{\text{cn}i}}}} \right)\frac{\left( {{T}^{t}}-{{T}^{t-\Delta t}} \right)}{\Delta t}.$ |
式中: t为当前时刻,Δt为时间步长,Vi为当前节点周围第i个单元的体积,nc为节点周围单元的总数,ncni为第i个单元的节点数.下标i代表第i个单元中心的变量值.
参考FEM的思想,利用型函数离散方程(1) 右端第一项
| $\oint{_{s}}k\frac{\partial T}{\partial {{x}_{\alpha }}}{{n}_{\alpha }}\text{dS}=\sum\limits_{i=1}^{{{n}_{c}}}{{{k}_{i}}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{{{T}_{ij}}}\int{_{sj}}\frac{\partial {{N}_{ij}}}{\partial {{x}_{\alpha }}}{{n}_{\alpha }}\text{dS}.$ |
式中:N为型函数,下标ij代表第i个单元中第j个节点上的变量值.
考虑边界条件,对于边界SD上的节点,其温度直接根据式(2) 给定.对于边界SN和SR上的节点,将式(3) 和(4) 代入,得到热传导方程的最终离散形式:
| $\begin{align} & \left( \sum\limits_{i=1}^{{{n}_{c}}}{\frac{{{\rho }_{i}}{{c}_{i}}{{V}_{i}}}{{{n}_{\text{cn}i}}}} \right)\frac{\left( {{T}^{t}}-{{T}^{t-\Delta t}} \right)}{\Delta t}=\sum\limits_{i=1}^{{{n}_{c}}}{{{k}_{i}}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{T_{_{ij}}^{t}}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\alpha }}}}{{n}_{\alpha }}\text{dS}- \\ & \sum\limits_{i=1}^{nN}{{{q}_{B}}}\left| {{A}_{Bi}} \right|-\sum\limits_{i=1}^{{{n}_{R}}}{{{h}_{B}}}\left( T-{{T}_{\infty }} \right)\left| {{A}_{Bi}} \right|. \\ \end{align}$ |
式中:ABi为与节点相邻的第i个边界单元面的面积矢量.nN为与当前节点相邻的位于SN上的面单元数,nR为与当前节点相邻的位于SR上的面单元数.
2.2 热弹性方程的离散利用中心差分格式离散热弹性方程(5) 左端的二阶时间项,得
| $\begin{align} & \sum\limits_{i=1}^{nN}{{{q}_{B}}}\left| {{A}_{Bi}} \right|-\sum\limits_{i=1}^{{{n}_{R}}}{{{h}_{B}}}\left( T-{{T}_{\infty }} \right)\left| {{A}_{Bi}} \right|. \\ & \int{_{V}\rho c\frac{{{\partial }^{2}}{{u}_{\alpha }}}{\partial {{t}^{2}}}}\text{d}V=\left( \sum\limits_{i=1}^{{{n}_{c}}}{\frac{{{\rho }_{i}}{{V}_{i}}}{{{n}_{\text{cn}i}}}} \right)\frac{u_{\alpha }^{t}-2u_{\alpha }^{t-\Delta t}+u_{\alpha }^{t-2\Delta t}}{\Delta {{t}^{2}}}. \\ \end{align}$ |
参考热传导方程空间项的离散方法,离散热弹性方程(5) 右端第一项和第二项
| $\begin{align} & \oint{s}\left[ G\left( \frac{\partial {{u}_{\alpha }}}{\partial {{x}_{\beta }}}+\frac{\partial {{u}_{\beta }}}{\partial {{x}_{\alpha }}} \right){{n}_{\beta }}+\lambda \left( \frac{\partial {{u}_{\gamma }}}{\partial {{x}_{\gamma }}} \right){{\delta }_{\alpha \beta }}{{n}_{\beta }} \right]\text{dS}- \\ & \oint{s}\Gamma a\left( T-{{T}_{r}} \right){{\delta }_{\alpha \beta }}{{n}_{\beta }}\text{dS}= \\ & \sum\limits_{i=1}^{{{n}_{c}}}{{{G}_{i}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{\left( {{u}_{\alpha ij}}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\beta }}}{{n}_{\beta }}\text{dS}+{{u}_{\beta ij}}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\alpha }}}{{n}_{\beta }}\text{dS}}} \right)}}+ \\ & \sum\limits_{i=1}^{{{n}_{c}}}{{{\lambda }_{i}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{\left( {{u}_{\gamma ij}}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\gamma }}}{{n}_{\alpha }}\text{dS}} \right)}}- \\ & \sum\limits_{i=1}^{{{n}_{c}}}{\left[ \Gamma a\left( \sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{\frac{{{T}_{ij}}}{{{n}_{\text{cn}i}}}}-{{T}_{r}} \right){{A}_{\alpha i}} \right]}. \\ \end{align}$ |
考虑边界条件,对于SD上的节点,位移给定为uαB.对于SN上的点,将式(6) 代入得到热弹性方程的最终离散形式
| $\begin{align} & {{M}^{u}}\frac{u_{\alpha }^{t}-2u_{\alpha }^{t-\Delta t}+u_{\alpha }^{t-2\Delta t}}{\Delta {{t}^{2}}}= \\ & \sum\limits_{i=1}^{{{n}_{c}}}{{{G}_{i}}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{{}}\left( u_{\alpha ij}^{t}\int {{S}_{i}}\frac{\partial {{N}_{ij}}}{\partial {{x}_{\beta }}}{{n}_{\beta }}\text{dS}+u_{\beta ij}^{t}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\alpha }}}{{n}_{\beta }}\text{dS}} \right)+ \\ & \sum\limits_{i=1}^{{{n}_{c}}}{{{\lambda }_{i}}\sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{\left( u_{\gamma ij}^{t}\int_{{{S}_{i}}}{\frac{\partial {{N}_{ij}}}{\partial {{x}_{\gamma }}}{{n}_{\alpha }}\text{dS}} \right)-}} \\ & \sum\limits_{i=1}^{{{n}_{c}}}{\left[ {{\Gamma }_{i}}{{a}_{i}}\left( \sum\limits_{j=1}^{{{n}_{\text{cn}i}}}{\frac{1}{{{n}_{\text{cn}i}}}}--{{T}_{r}} \right){{A}_{\alpha i}} \right]}+\sum\limits_{i=1}^{{{n}_{\text{N}}}}{{{\sigma }_{\alpha \text{B}}}}{{A}_{\text{B}i}}\cdot \\ \end{align}$ |
采用Fortran语言编程实现本文的数值方法.文献[16-18]采用分离解法求解不同方向的位移方程,即在求解某一方向的位移时,相关的其它位移采用上一次的计算结果,迭代求解各方向位移,直到获得收敛解.区别于上述文献,本文采用耦合解法同时求解3个方向位移,从而1次计算即可获得位移场.不同网格单元的型函数表达式见文献[18].
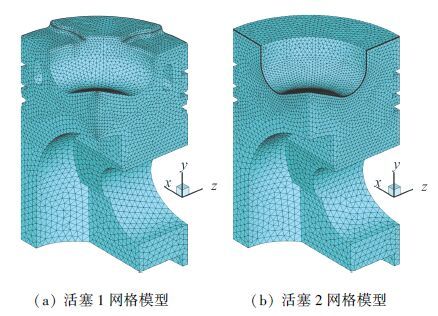
3 活塞计算模型 3.1 活塞几何模型及网格模型模拟活塞热应力问题,考虑到活塞几何形状的对称性,取如图 2所示的1/4模型,活塞直径为170 mm.活塞模型1与模型2的区别在于,活塞模型1上表面具有避阀坑,没有布置TBC,通过冷却油道冷却活塞头部;而活塞模型2上表面被简化了,没有避阀坑,布置有TBC,没有冷却油道,利用TBC的隔热作用保护活塞头部.采用四面体单元和棱柱单元划分计算域,见图 2.
|
图 2 活塞网格模型 |
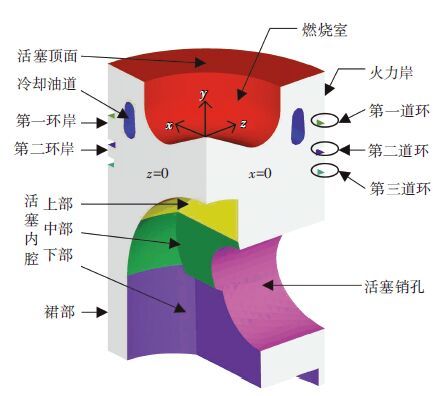
以活塞2为例给出计算边界条件.活塞x=0及z=0(见图 3)平面为对称面,设为绝热边界,给定简支位移约束.为了避免活塞的刚体平移,活塞底面给定简支约束边界条件.参考文献[19]中的活塞表面对流换热系数和环境温度(由技术参数和经验公式得到),取平均值做稳态计算.活塞热边界条件见图 3和表 1.活塞物性参数见表 2.
|
图 3 活塞边界 |
| 表 1 活塞热边界条件 |
| 表 2 活塞物性参数 |
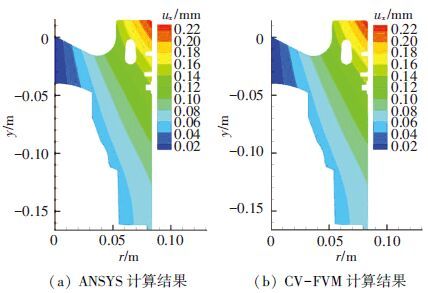
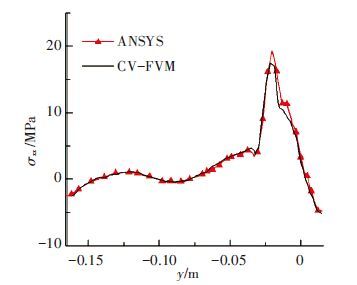
为验证本文数值方法的正确性,数值模拟普通活塞1的热应力场,活塞材料为硅铝合金.图 4为不同方法计算得到的45°平面上位移ux云图.图 5为不同方法计算的45°平面r=0.072 m处的应力σxx曲线,其中r=0.072 m位于冷却油腔和活塞环槽之间,热应力场较为复杂.通过对比可以看出,本文发展的三维CV-FVM计算结果与ANSYS计算结果一致,说明本文三维CV-FVM可用于活塞热应力数值模拟.
|
图 4 活塞1的x方向位移云图对比(45°平面) |
|
图 5 活塞1的应力σxx曲线对比(45°平面上r=0.072 m处) |
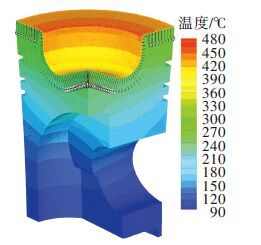
在活塞顶面涂覆1 mm的TBC.活塞基体为铝硅合金ZL 109,粘结材料为NiCrAl(厚度为0.2 mm),陶瓷材料为MgZrO3(厚度为0.8 mm),材料物性参数见表 2.图 6给出了活塞的表面热流矢量及温度分布云图.活塞2表面的TBC承受了大部分的热载荷,热流量集中于TBC区域,活塞上表面温度明显高于活塞基体温度.
|
图 6 活塞2的表面热流矢量及温度云图 |
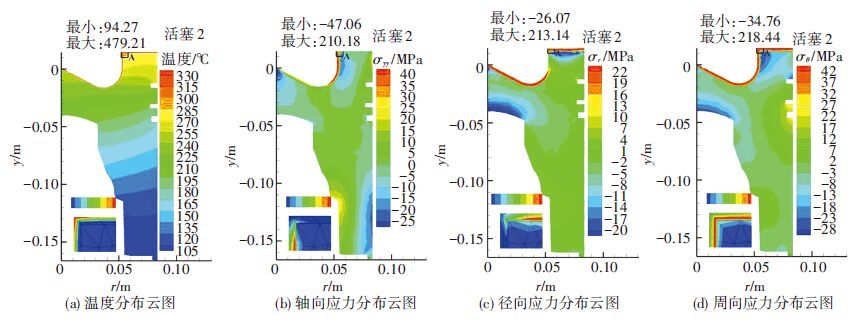
图 7为活塞2内θ=45°平面上的热应力场云图.由图可见,活塞的最大温度T位于燃烧室与活塞顶面的交界区域(A区域),主要原因是A区为活塞上表面转折位置,相较于其它位置热阻更大,热量传递更少,因而温度越高.轴向应力σyy、径向应力σr和周向应力σθ幅值相当,其最大值位于粘结层与陶瓷层的分界面附近,主要原因是陶瓷层阻隔了大部分的热量,相对而言传递到粘结层、金属基体的热量较小,故陶瓷层和粘结层之间的温度梯度比粘结层和金属基体间的温度梯度大得多,陶瓷层和粘结层间存在更大的热应力.由于TBC内物性参数的突变,TBC区域存在明显的应力集中现象,容易发生破坏.
|
图 7 活塞2的θ=45°平面上热应力场云图 |
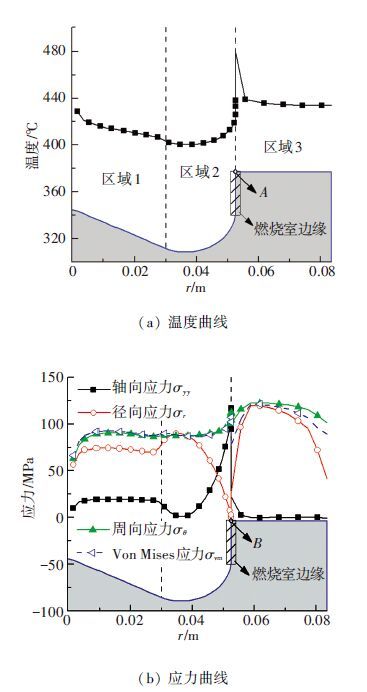
分析TBC活塞2上表面θ=45°处的温度及应力曲线,见图 8.
|
图 8 活塞2的上表面θ=45°线上热力曲线 |
燃烧室顶面包含3个区域:区域1、区域2位于燃烧室,区域3是活塞顶面.燃烧室边缘区域用斜线标出.温度最小值位于区域2,最大值位于B点.参考温度曲线,可以看到在燃烧室边缘区域温度梯度最大,应力在该区域变化幅值相对其他区域大得多.与应力σr和σyy相比,应力σθ沿径向变化平缓且幅值最大.Von Mises应力σvm可代表活塞的综合应力情况,其变化趋势与应力σθ基本一致,说明应力σθ对活塞的整体应力水平起主要影响.
5 结论1) 本文基于CV-FVM求解热传导方程和热弹性方程,将适用于二维复合材料热应力问题的CV-FVM推广应用于三维热应力问题.采用CV-FVM分析普通活塞的热应力问题,计算结果与商用软件ANSYS计算结果吻合良好,表明该方法的正确性.
2) 基于CV-FVM进一步分析TBC活塞热应力场.通过分析活塞热应力场可知,陶瓷层能够阻隔活塞顶面的大部分热量,使得粘结层和陶瓷层间存在较大温度梯度,引起应力集中,应力最大值出现在粘结层和陶瓷层分界面区域.
3) 通过分析TBC活塞热应力曲线可知,温度最大值出现在燃烧室与活塞顶面的交界区域,活塞的应力水平主要受周向应力σθ影响.
4) TBC活塞热应力场没有出现数值不连续现象,CV-FVM能够作为TBC活塞热力性能研究的数值预测工具.
| [1] |
王素, 倪春阳, 朱心雄. 功能梯度材料活塞三维温度场分析[J].
北京航空航天大学学报,2005, 31 (12) : 1299-1302.
( 0) 0)
|
| [2] |
王素, 倪春阳, 朱心雄. 一种功能梯度材料活塞的材料梯度方程选择[J].
机械科学与技术,2006, 25 (2) : 133-138.
( 0) 0)
|
| [3] |
王素, 倪春阳, 朱玉明, 等. 陶瓷纤维梯度增强活塞的梯度方程研究[J].
航空学报,2007, 28 (1) : 234-239.
( 0) 0)
|
| [4] |
BUYUKKAYA E, CERIT M. Thermal analysis of a ceramic coating diesel engine piston using 3-D finite element method[J].
Surface and Coatings Technology,2007, 202 (2) : 398-402.
( 0) 0)
|
| [5] |
BUYUKKAYA E. Thermal analysis of functionally graded coating AlSi alloy and steel pistons[J].
Surface and Coatings Technology,2008, 202 (16) : 3856-3865.
( 0) 0)
|
| [6] |
CERIT M. Thermo mechanical analysis of a partially ceramic coated piston used in an SI engine[J].
Surface and Coatings Technology,2011, 205 (11) : 3499-3505.
( 0) 0)
|
| [7] |
CERIT M, AYHAN V, PARLAK A, et al. Thermal analysis of a partially ceramic coated piston: Effect on cold start HC emission in a spark ignition engine[J].
Applied Thermal Engineering,2011, 31 (2/3) : 336-341.
( 0) 0)
|
| [8] |
ABOUDI J, PINDERA M J, ARNOLD S M. Higher-order theory for functionally graded materials[J].
Composites, Part B,1999, 33 : 777-832.
( 0) 0)
|
| [9] |
SANTARE M H, LAMBROS J. Use of graded finite elements to model the behavior of nonhomogeneous materials[J].
ASME Journal of Applied Mechanics,2000, 67 (4) : 819-822.
( 0) 0)
|
| [10] |
KIM J H, PAULINO G H. Isoparametric graded finite elements for nonhomogeneous isotropic and orthotropic materials[J].
ASME Journal of Applied Mechanics,2002, 69 (4) : 502-514.
( 0) 0)
|
| [11] |
CAVALCANTE M A A, MARQUES S P C, PINDERA M J. Parametric formulation of the finite-volume theory for functionally graded materials-Part II: numerical results[J].
Journal of Applied Mechanics,2007, 74 (5) : 946-957.
( 0) 0)
|
| [12] |
GONG J F, XUAN L K, MING P J, et al. Thermoelastic analysis of functionally graded solids using a staggered finite volume method[J].
Composite Structures,2013, 104 : 134-143.
( 0) 0)
|
| [13] |
GONG J F, XUAN L K, MING P J, et al. An unstructured finite-volume method for transient heat conduction analysis of multilayer functionally graded materials with mixed grids[J].
Numerical Heat Transfer: Part B,2013, 63 (3) : 222-247.
( 0) 0)
|
| [14] |
GONG J F, XUAN L K, MING P J, et al. Application of the staggered cell-vertex finite volume method to thermoelastic analysis in heterogeneous materials[J].
Journal of Thermal Stresses,2014, 37 (4) : 506-531.
( 0) 0)
|
| [15] |
龚京风, 明平剑, 宣领宽, 等. 基于有限体积法求解FGM动态响应及固有特性[J].
华中科技大学学报(自然科学版),2013, 41 (5) : 28-33.
( 0) 0)
|
| [16] |
TAYLOR G A, BAILEY C, CROSS M. Solution of the elastic/visco-plastic constitutive equations: a finite volume approach[J].
Applied Mathematical Modelling,1995, 19 (12) : 746-760.
( 0) 0)
|
| [17] |
BAILEY C, CROSS M. A finite volume procedure to solve elastic solid mechanics problems in three dimensions on an unstructured mesh[J].
International Journal for Numerical Methods in Engineering,1995, 38 (10) : 1757-1776.
( 0) 0)
|
| [18] |
TAYLOR G A, BAILEY C, CROSS M. A vertex-based finite volume method applied to non-linear material problems in computational solid mechanics[J].
International Journal for Numerical Methods in Engineering,2003, 56 (4) : 507-529.
( 0) 0)
|
| [19] |
刘友. 船用柴油机活塞瞬态温度场测试与分析研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


