张拉整体结构是由离散的压杆和连续的拉索组成的自平衡、自支撑结构,是一种新型空间结构体系. 自从张拉整体结构诞生以来,学者们从不同的方向对该结构进行了广泛研究. Zhang等[1]在张拉整体棱柱结构的基础上,提出了双面“星形”张拉整体结构;Skelton等[2-4]利用张拉整体棱柱拓扑得到了“塔形”张拉整体结构,完成了该结构的构型和力学分析;Pellegrino等[5-7]提出了利用结构的自应力模态数和机构位移模态数对索杆张拉结构体系进行分类,通过矩阵分析判定结构的几何稳定性;Guest[8-9]通过构件的力平衡方程得到结构的切线刚度矩阵,并对切线刚度矩阵各部分的物理意义进行了分析. 在Pellegrino和Calladine提出的索杆结构体系分类理论基础上,Lazopulos等[10-11]对第Ⅳ类体系的几何稳定判定方法进行了更深入的研究;罗尧治等[12-13]对索杆张力结构体系的几何稳定性和可动性进行了细致全面的研究. 现有文献对基本单元的研究主要集中在3根杆等长、9根索等长,且具有严格对称性的结构.
为了构建形式更为多样的空间大型结构,有必要对基本单元进行扩展性探索. 本文从基本单元节点广义坐标出发,构建基本体数学模型和力学模型,解决基本单元稳定构型问题.
1 结构的数学模型张拉整体结构是由节点、索构件、杆构件组成的. 搭建张拉整体结构,必须要确定各构件的结构尺寸. 所有构件均与节点关联,因此从节点出发,构建结构数学模型,获得构件尺寸与结构几何参数的关系.
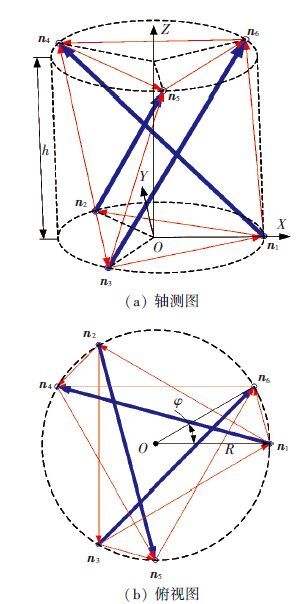
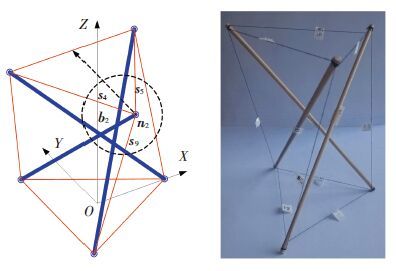
1.1 节点矢量矩阵张拉整体三棱柱由6个节点、3根压杆和9根拉索组成,如图 1所示,图中虚线表示结构包络外形,粗实线表示杆构件,细实线表示索构件,箭头表示各构件矢量方向. 张拉整体三棱柱外接一圆柱体,设此圆柱体的截面圆半径为R,圆柱体的高度为h. 顶面和底面三角形存在一个相位角[14-15],设此相位角为φ.
|
图 1 张拉整体三棱柱 |
建立如图 1所示的直角坐标系,分析数学模型和几何参数之间的函数关系.
结构下底面的节点位置可分别表示为
| $\begin{align} & {{n}_{1}}={{\left[ R\text{ }0\text{ }0 \right]}^{\text{T}}}, \\ & {{n}_{2}}={{\left[ R\cos \left( \frac{2}{3}\pi \right)\text{ }R\sin \left( \frac{2}{3}\pi \right)\text{ }0 \right]}^{\text{T}}}, \\ & {{n}_{3}}={{\left[ R\cos \left( \frac{4}{3}\pi \right)\text{ }R\sin \left( \frac{4}{3}\pi \right)\text{ }0 \right]}^{\text{T}}}. \\ \end{align}$ |
结构上底面节点位置可表示为
| $\begin{align} & {{n}_{4}}={{\left[ R\cos \left( \frac{2}{3}\pi +\varphi \right)\text{ }R\sin \left( \frac{2}{3}\pi +\varphi \right)\text{ }h \right]}^{\text{T}}}, \\ & {{n}_{5}}={{\left[ R\cos \left( \frac{4}{3}\pi +\varphi \right)\text{ }R\sin \left( \frac{4}{3}\pi +\varphi \right)\text{ }h \right]}^{\text{T}}}, \\ & {{n}_{6}}={{\left[ R\cos \varphi \text{ }R\sin \varphi \text{ }h \right]}^{\text{T}}}. \\ \end{align}$ |
将结构两底面的节点坐标按顺序组合,可得表示所有节点位置的节点矢量矩阵N,且
| $N={{\left[ {{n}_{1}}\text{ }{{n}_{2}}\text{ }{{n}_{3}}\text{ }{{n}_{4}}\text{ }{{n}_{5}}\text{ }{{n}_{6}} \right]}_{3\times 6}}.$ |
结构中各构件都连接于节点上,因此可以通过节点来确定构件矢量. 由图 1可知节点与杆索构件矢量的连接关系,构件与节点的连接关系列于表 1和表 2.
| 表 1 杆与节点的连接关系 |
| 表 2 索与节点的连接关系 |
由表 1可知,第i个杆构件矢量可表示为
| ${{b}_{i}}={{n}_{i+3}}-{{n}_{i}},i\in \left[ 1,3 \right].$ |
所有杆构件矢量按列组合,形成结构的杆矢量矩阵为
| $B=\left[ {{b}_{1}}{{b}_{2}}{{b}_{3}} \right]=NC_{B}^{\text{T}}=N\left[ \begin{array}{*{35}{l}} -1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & -1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right].$ |
结构中索矢量矩阵可表示为
| $S=\left[ {{s}_{1}}{{s}_{2}}...{{s}_{9}} \right]=NC_{S}^{\text{T}}\in {{\mathbb{R}}^{3\times 9}}.$ |
式中: 矩阵CST为索连接矩阵,表示节点矩阵与索矢量矩阵的连接关系
| $C_{S}^{\text{T}}={{\left[ \begin{array}{*{35}{l}} -1 & 0 & 1 & 0 & 0 & 0 & -1 & 0 & 0 \\ 1 & -1 & 0 & 0 & 0 & 0 & 0 & -1 & 0 \\ 0 & 1 & -1 & 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & -1 & 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & -1 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 & -1 & 1 & 0 & 0 \\ \end{array} \right]}_{6\times 9}}.$ |
由CBT及CST即可建立索、杆构件矢量与节点矢量的关系. 通过构件矢量矩阵,可获得各索杆构件矢量,从而得到各构件长度,这样即可搭建图 1所示的结构.
2 结构的平衡状态分析 2.1 外部载荷在张拉整体结构的3个要素中,索构件在承受外部载荷时可能处于拉伸状态,也可能处于放松状态,其自由度很难确定;杆构件在外部载荷的作用下有6个自由度;节点在外部载荷的作用下只有3个自由度. 所以,以系统的节点广义坐标矢量矩阵为基础定义外部载荷,可以在很大程度上减小理论分析的过程和难度,具有显著的优越性.
张拉整体三棱柱结构的外部载荷作用于其节点上,结构中节点i上的外部载荷表示为
| ${{w}_{i}}={{\left[ {{w}_{ix}}{{w}_{iy}}{{w}_{iz}} \right]}^{\text{T}}},$ |
那么,结构中所有节点的外部载荷可以用矩阵W表示,将其命名为外力矩阵:
| $W={{\left[ {{w}_{1}}{{w}_{2}}...{{w}_{6}} \right]}_{3\times 6}}.$ |
外力也可以表示为列向量的形式,即
| $W=\left[ w_{1}^{\text{T}}w_{2}^{\text{T}}...w_{6}^{\text{T}} \right]_{_{18\times 1}}^{\text{T}}.$ |
当结构处于稳定状态时,每个节点都在外部载荷和构件内力作用下保持平衡. 为确定构件内力与构件矢量的关系,引入力密度[12]. 设杆构件i的力密度为λi(λi≥0) ,此构件的内力可表示为
| ${{f}_{bi}}={{\lambda }_{i}}{{b}_{i}}.$ |
设索构件j的力密度为γj(γj≥0) ,其内力可表示为
| ${{f}_{sj}}={{\gamma }_{j}}{{s}_{j}}.$ |
那么,结构中索构件力密度和杆构件力密度可分别表示为
| $\begin{align} & \lambda ={{\left[ \begin{matrix} {{\lambda }_{1}} \\ {{\lambda }_{2}} \\ {{\lambda }_{3}} \\ \end{matrix} \right]}_{3\times 1}},\lambda ={{\left[ \begin{array}{*{35}{l}} {{\lambda }_{1}} & 0 & 0 \\ 0 & {{\lambda }_{2}} & 0 \\ 0 & 0 & {{\lambda }_{3}} \\ \end{array} \right]}_{3\times 3}}, \\ & \gamma ={{\left[ \begin{matrix} {{\gamma }_{1}} \\ {{\gamma }_{2}} \\ \vdots \\ {{\gamma }_{9}} \\ \end{matrix} \right]}_{9\times 1}},\gamma ={{\left[ \begin{array}{*{35}{l}} {{\gamma }_{1}} & 0 & \cdots & 0 \\ 0 & {{\gamma }_{2}} & \cdots & 0 \\ \vdots & \vdots & {} & \vdots \\ 0 & 0 & \cdots & {{\gamma }_{9}} \\ \end{array} \right]}_{9\times 9}}. \\ \end{align}$ |
矩阵${\hat{\gamma }}$是矩阵γ的对角阵,矩阵${\hat{\lambda }}$是矩阵λ的对角阵.
2.3 结构的力平衡方程在张拉整体三棱柱的节点ni处于平衡状态时,有
| ${{w}_{{{i}_{3\times 1}}}}={{N}_{3\times 3}}{{k}_{i}},$ | (1) |
式中:
| $\begin{align} & {{k}_{i}}=C_{{{S}_{6\times 9}}}^{\text{T}}{{{\hat{\gamma }}}_{9\times 9}}{{C}_{{{S}_{{{i}_{9\times 1}}}}}}-C_{{{B}_{6\times 3}}}^{\text{T}}{{{\hat{\lambda }}}_{3\times 3}}{{C}_{{{B}_{{{i}_{3\times 1}}}}}}= \\ & C_{{{S}_{6\times 9}}}^{\text{T}}{{{\hat{C}}}_{{{S}_{{{i}_{9\times 9}}}}}}{{\gamma }_{9\times 1}}-C_{{{B}_{6\times 3}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{{{i}_{3\times 3}}}}}}{{\gamma }_{3\times 1}}= \\ & \left[ C_{{{S}_{6\times 9}}}^{\text{T}}{{{\hat{C}}}_{{{S}_{{{i}_{9\times 9}}}}}}\left| - \right.C_{{{B}_{6\times 3}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{{{i}_{3\times 3}}}}}} \right]{{\left[ \begin{matrix} \gamma \\ \lambda \\ \end{matrix} \right]}_{12\times 1}}. \\ \end{align}$ | (2) |
其中,矩阵CS为索连接矩阵CST的转置,CSi为矩阵CS的第i列,${{{\hat{C}}}_{{{S}_{{{i}_{{}}}}}}}$为矩阵CS第i列的对角阵,矩阵CB为杆连接矩阵CBT的转置,CBi为矩阵CB的第i列,${{{\hat{C}}}_{{{B}_{i}}}}$为矩阵CB第i列的对角阵.
将等式(2) 带入等式(1) ,可得
| $\begin{align} & {{w}_{{{i}_{3\times 1}}}}={{N}_{3\times 6}}{{\left[ C_{S}^{\text{T}}{{{\hat{C}}}_{{{S}_{1}}}}\left| NC_{{{B}_{{}}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{i}}}} \right. \right]}_{6\times 12}}{{\left[ \begin{matrix} \gamma \\ \lambda \\ \end{matrix} \right]}_{12\times 1}}= \\ & {{\left[ NC_{S}^{\text{T}}{{{\hat{C}}}_{{{S}_{1}}}}\left| - \right.NC_{{{B}_{{}}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{i}}}} \right]}_{3\times 12}}{{\left[ \begin{matrix} \gamma \\ \lambda \\ \end{matrix} \right]}_{12\times 1}}, \\ \end{align}$ |
进一步推导,可得整个结构的力平衡方程:
| $w={{A}_{18\times 12}}{{\left[ \begin{matrix} \gamma \\ \lambda \\ \end{matrix} \right]}_{12\times 1}}.$ | (3) |
式中:w是外力列矢量,A是系统平衡矩阵,
| $A={{\left[ \begin{matrix} NC_{S}^{\text{T}}{{{\hat{C}}}_{{{S}_{1}}}}\left| - \right.NC_{{{B}_{{}}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{1}}}} \\ NC_{S}^{\text{T}}{{{\hat{C}}}_{{{S}_{2}}}}\left| - \right.NC_{{{B}_{{}}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{2}}}} \\ \vdots \\ NC_{S}^{\text{T}}{{{\hat{C}}}_{{{S}_{6}}}}\left| - \right.NC_{{{B}_{{}}}}^{\text{T}}{{{\hat{C}}}_{{{B}_{6}}}} \\ \end{matrix} \right]}_{18\times 12}}.$ |
外载荷、几何参数及力密度构成了系统力平衡线性方程组. 求解方程(3) ,即可评价系统的受力状态. 该方程有非负力密度标量解,是系统能够处于平衡状态,且杆只受压力、索只受拉力的先决条件. 下面就从平衡矩阵分析角度出发,进行系统稳定性判定.
3 结构的稳定性判定 3.1 结构稳定性在张拉整体三棱柱结构中,每个节点连接3根索和1根杆. 由于索构件只承受拉力,杆构件只承受压力,结构若在节点处保持力平衡和几何稳定,则在自应力模态下杆构件必须位于以节点为顶点、以3根索为棱边构成的三棱锥锥体几何空间的内部. 同时,结构相位角直接影响系统稳定性.
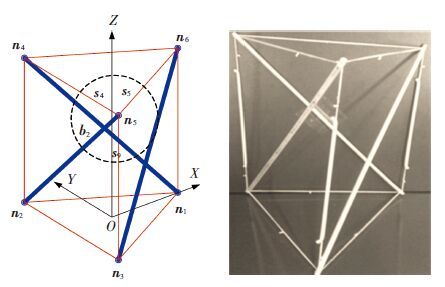
当结构的相位角φ=0(如图 2所示)时,所有构件均处于三棱柱外表面(面n1n2n4n6、面n2n3n5n4、面n3n1n6n5)上. 连接于同一节点的4个构件中,杆与一根端面索及连接两个端面的索这3个构件共面,其合力与第4个构件的内力无法平衡,因此任何节点在无外载荷情况下,不能实现自应力平衡,即整个结构不是自应力稳定结构. 图 2右侧的物理模型必须在外力作用下才能够实现该位置结构平衡,证实了该位置结构不能达到自应力平衡.
|
图 2 临界状态φ=0(构件布置在三棱柱外表面) |
当相位角φ=π/3(如图 3所示)时,3根杆交于杆中点,所有构件均在三棱柱3个对角平面(面n1n2n4n5、面n2n3n5n6、面n3n1n6n4)上. 任一节点4个构件有3个共面,因此无法施加预应力达到结构自应力平衡状态. 右侧物理模型需要约束3根杆交点才能够实现结构平衡,证实了该位置结构不能自应力平衡稳定.

|
图 3 临界状态φ=π/3(构件都布置在棱柱对角面) |
通过求解系统平衡方程式(3) ,利用方程解的情况来分析结构是否稳定. 为了分析方程的解,应用奇异值分析方法(SVD),对系统平衡矩阵进行分析,结合自应力模态数和位移模态数判断系统稳定性.
平衡矩阵$A\in {{\mathbb{R}}^{18\times 12}}$,A的秩为rA,存在酉阵$U\in {{\mathbb{R}}^{18\times 18}}$,使得
| $A=U\left[ \begin{matrix} \left[ D \right]{{r}_{A}}\times {{r}_{A}} & 0 \\ 0 & 0 \\ \end{matrix} \right]{{V}^{\text{T}}}.$ |
式中:
| $\left[ D \right]{{r}_{A}}\times {{r}_{A}}=diag\left[ {{D}_{11}}{{D}_{22}}\cdots {{D}_{{{r}_{A}}\times {{r}_{A}}}} \right],$ |
D11≥D22≥....≥DnrA×rA≥0为非零奇异值,U和V均为正交阵. 记
| $U=\left[ {{U}_{{{r}_{A}}}}{{U}_{18-{{r}_{A}}}} \right],V=\left[ {{V}_{{{r}_{A}}}}{{V}_{12-{{r}_{A}}}} \right].$ |
张拉整体三棱柱结构的自应力模态数s和位移模态数m分别为 s=p+q-rA,
| $\left\{ \begin{matrix} S=p+q-{{r}_{A}}, \\ m=3\left( n-k \right)-{{r}_{A}}. \\ \end{matrix} \right.$ | (4) |
式中:p为杆构件数量,q为索构件数量,n为节点数,k为约束节点的数量(本文中k=3,约束节点n1-n3).
通过自应力模态数s和位移模态数m便可初步判断结构的几何稳定性. 文献[5-7]中,在机构位移模态数m和自应力模态数s的基础上对杆系结构进行了分类,见表 3.
| 表 3 结构体系分类 |
类型I为静定结构,无机构位移模态和自应力模态,不可施加预应力,不可发生零应变几何变位. 类型Ⅱ为有限机构,不可施加预应力,可以有零应变几何大变位. 类型Ⅲ为超静定结构,可施加预应力,实现自应力平衡. 类型Ⅳ可以施加预应力,可以有零应变几何大变位;若自应力能够刚化应变,则几何稳定,通常称为无限小机构[14].
3.2.2 第Ⅳ类结构几何稳定性当结构存在位移模态(m>0) 和自应力模态(s>0) 时,结构的节点处将产生几何力G,几何力G由相应的自应力模态和位移模态求解获得.
对于单一自应力模态(s=1) 体系,若对任意的非零向量βm ×1,满足
| ${{\beta }^{\text{T}}}\left( {{G}^{\text{T}}}{{U}_{18-rA}} \right)\beta >0.$ | (5) |
则表明各机构位移模态的任意组合,都将在自应力下得到刚化结构几何稳定.
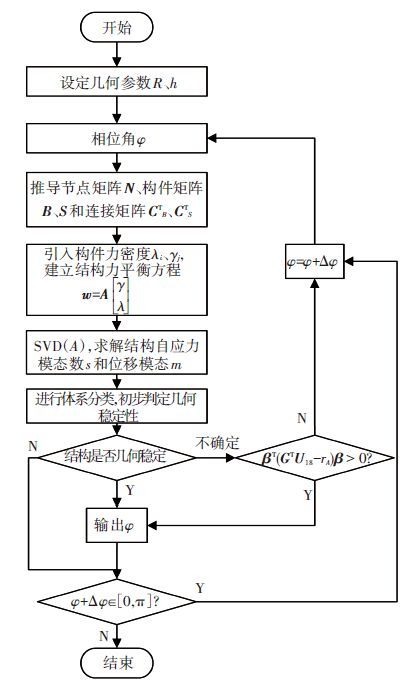
3.3 分析结构自应力稳定条件通过分析结构的平衡矩阵,获得平衡矩阵的秩及自应力模态数s和位移模态数m值. 利用MATLAB程序(程序框图如图 4所示),以及式(4) 和表 3对结构(三棱柱的结构参数R=0.5 m,h=1 m)的稳定性进行判断.
|
图 4 稳定性判断流程图 |
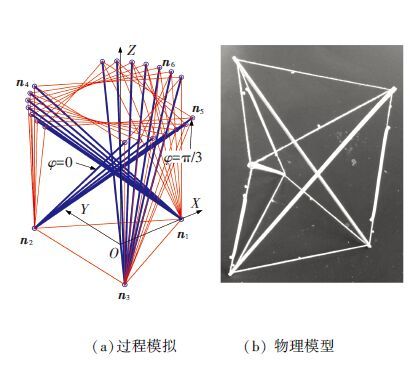
张拉整体三棱柱结构的相位角变化对结构体系分类影响的分析过程如图 5所示. 相位角φ∈(0,π/3) 变化时,结构的仿真模拟如图 5(a)所示,s和m的具体结果如表 4所示.
|
图 5 稳定性判断结构 |
| 表 4 相位角与位移模态数和自应力模态数 |
由表 3和参考文献[5-7]可知,当相位角φ∈[0,π/6) ∪(π/6,π/3],属于第I类结构体系,结构是静定、动定体系;不可施加预应力,不可有几何变位;对于给定的外载荷有唯一的稳定状态;不能构成自应力稳定结构、可以构建外载荷下唯一的结构形式.
为了验证方法及程序仿真分析的正确性和可行性,制作了物理模型(如图 5(b)所示,索s7-s9使用弹性材料以便适应相位角φ变化时索长的变化),设定R=10,h=20,进行不同相位角,结构稳定性物理模型验证.
相位角φ=π/6(如图 6所示),结构的位移模态数m=1,自应力模态数s=1,结构属于第Ⅳ类体系,结构的稳定性还需要进一步判断.
|
图 6 张拉整体三棱柱(φ=π/6) |
通过等式(5) ,求得三棱柱结构在相位角φ=π/6时βT(GTU18-rA)β=0.064 1,满足自应力刚化结构几何变位条件,即结构为无限小机构,能够实现自应力平衡稳定结构.
从节点受力角度来理解不同相位角下结构的稳定性问题. 当相位角φ=π/6时,无外载荷的情况下,任一节点受到的端面索合拉力、杆支撑力、端面间索拉力3个力共面,总合力为零,节点能够在自应力作用下达到力平衡稳定状态,即整个系统是可以施加预应力的自应力稳定结构. 当相位角φ∈[0,π/6) ∪(π/6,π/3]时,无外载荷的情况下,任意节点受到的杆构件的力、端面间索拉力,不可能与端面索合力共面,也即任意节点的合力不能为零,节点不能在预应力下达到自平衡状态,即结构不能实现自应力平衡.
综上,要构建3杆9索张拉整体三棱柱自应力平衡稳定结构,其相位角应该满足φ=π/6.
4 结论1) 以张拉整体三棱柱结构的几何外形参数为基础,构建节点广义坐标矢量矩阵、构件矢量矩阵和节点与构件之间的连接矩阵,建立基于节点广义坐标的结构自动构型数学模型.
2) 基于系统力平衡及节点受力分析,引入力密度参量,把构件力与构件矢量直接联系起来;构建三棱柱结构系统基于节点广义坐标与连接矩阵的关于力密度非负标量参数的线性力学模型.
3) 通过分析系统平衡矩阵,利用结构的自应力模态和机构位移模态得到结构的几何力,以几何力为判据,完成了结构几何外形参数相位角取值范围的判定.
4) 拓展了传统基本单元构型过程中所有索段长度相同的限制条件,提出了能够适用于不同几何外形参数的三棱柱单元的稳定构型理论.
| [1] |
ZHANG J Y, GUEST S D, CONNELLY R, et al. Dihedral ‘star’ tensegrity structures[J].
International Journal of Solids and Structures,2010, 47 (1) : 1-9.
( 0) 0)
|
| [2] |
De OLIVEIRA M C, SKELTON R E. A new topology of tensegrity towers with uniform force distribution[C]//Proceedings of the society of photo-optical instrumentation engineers (SPIE). San Diego: SPIE, 2005: 198-208.
( 0) 0)
|
| [3] |
De OLIVEIRA M C, SKELTON R E, CHAN W L. Minimum mass design of tensegrity towers and plates[C]//IEEE Conference on Decision and Control. New York: IEEE, 2006: 2314-2319.
( 0) 0)
|
| [4] |
MASIC M, SKELTON R E. Optimization of class-2 tensegrity towers[C]//Proceedings of the society of photo-optical instrumentation engineers (SPIE). San Diego: SPIE, 2004: 163-174.
( 0) 0)
|
| [5] |
PELLEGRINO S, CALLADINE C R. Matrix analysis of statically and kinematically indeterminate frameworks[J].
International Journal of Solids and Structures,1986, 22 (4) : 409-428.
( 0) 0)
|
| [6] |
PELLEGRINO S. Analysis of prestressed mechanisms[J].
International Journal of Solids and Structures,1990, 26 (12) : 1329-1350.
( 0) 0)
|
| [7] |
PELLEGRINO S. Structural computations with the singular value decomposition of the equilibrium matrix[J].
International Journal of Solids and Structures,1993, 30 (21) : 3025-3035.
( 0) 0)
|
| [8] |
GUEST S D. The stiffness of prestressed frameworks: A unifying approach[J].
International Journal of Solids and Structures,2006, 43 (3/4) : 842-854.
( 0) 0)
|
| [9] |
GUEST S D. The stiffness of tensegrity structures[J].
IMA Journal of Applied Mathematics,2011, 76 (1SI) : 57-66.
( 0) 0)
|
| [10] |
LAZOPULOS K A. Stability of an elastic cytoskeletal tensegrity model[J].
International Journal of Solids and Structures,2005, 42 (11/12) : 3459-3469.
( 0) 0)
|
| [11] |
LAZOPULOS K A. Stability of an elastic tensegrity structure[J].
Acta Mechanica,2005, 179 (1/2) : 1-10.
( 0) 0)
|
| [12] |
罗尧治, 陆金钰. 杆系结构可动性判定准则[J].
工程力学,2006 (11) : 70-75.
( 0) 0)
|
| [13] |
罗尧治. 索杆张力结构几何稳定性分析[J].
浙江大学学报(理学版),2000, 27 (6) : 608-611.
( 0) 0)
|
| [14] |
OLIVEIRA M C, SKELTON R E.
Tensegrity Systems[M]. [S.l.]: Springe, 2009 : 106 -110.
( 0) 0)
|
| [15] |
ZHANG P, KAWAGUCHI K I, FENG J. Prismatic tensegrity structures with additional cables: Integral symmetric states of self-stress and cable-controlled reconfiguration procedure[J].
International Journal of Solids and Structures,2014, 51 (25/26) : 4294-4306.
( 0) 0)
|
| [16] |
陆金钰. 动不定结构的平衡矩阵分析方法与理论研究[D]. 杭州:浙江大学, 2008:33-56.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


