2. 机械系统与振动国家重点实验室(上海交通大学), 上海 2002404 ;
3. 机器人技术与系统国家重点实验室(哈尔滨工业大学), 哈尔滨 150080 ;
4. 江苏省食品先进制造装备技术重点实验室(江南大学), 江苏 无锡 214122
2. State Key Laboratory of Mechanical System and Vibration(Shanghai Jiao Tong University), Shanghai 200240, China ;
3. State Key Laboratory of Robotics and System(Harbin Institute of Technology), Harbin 150080, China ;
4. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology(Jiangnan University), Wuxi 214122, Jiangsu, China
给定期望自由度和类型下的并联机器人构型综合,已经通过螺旋理论[1]、位移子群及位移流形[2]、PoC单元法[3]、 GF 集合理论[4]得到解决.但结合特殊运动性能的并联机构型综合问题并没有得到完全解决.运动耦合使并联机器人具有了不同于串联机器人的一些特性,比如承载力强、累计误差小等,也正由于运动耦合特性的存在导致并联机器人控制复杂,造成运动学和动力学分析困难.
相对于一般并联机构而言,完全各向同性解耦并联机构具有轨迹规划简单,实时控制容易,各向同性良好,精度高等优点,因此在低承载、高精度、高速度的应用领域,如手术机器人、微纳操作装备,解耦并联机构表现出独特优势[5].目前,国内外学者[6-10]对解耦、各向同性并联机构也做了诸多研究.2T2R并联机构把空间的移动和转动有机结合起来,在工业中得到广泛应用.例如可用该机构结合工作台的运动构成五轴联动数控机床,也可用做减振平台[11]、空间振动筛[12].但对于 2T2R 解耦并联机构的型综合研究却较少.基于线性变换理论,Gogu[13]提出了完全各向同性 2T2R 并联机构的型综合方法,张彦斌等[14]基于混联机构概念和互易螺旋理论提出了完全解耦 2T2R 并联机构型综合的方法;但是,上述所综合出的机构中都包含有一条混合链,不利于机构的生产加工.
本文介绍了GF集的概念.阐述了基于GF集的完全各向同性并联机构型综合理论,根据该理论提出了2T2R完全各向同性解耦并联机器人构型综合一般方法、设计步骤,并综合出具体构型,最后实例证明了其正确性.
1 GF集的基本概念 1.1 GF集的定义机器人末端一般运动特征的集合称之为 GF集.GF集由6个元素构成,即,
| ${{G}_{F}}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{a}}~{{R}_{\beta }}~{{R}_{\gamma }})$ |
式中:Ti(i=a,b,c)为机构末端移动特征;Rj(j=α,β,γ)为机构转动特征.
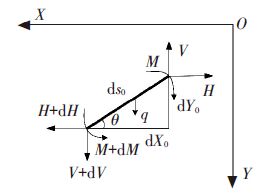
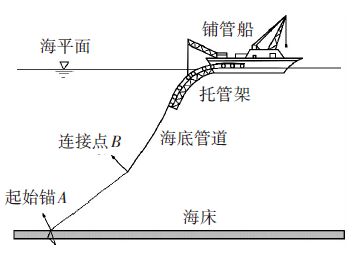
GF集可分为2类:第1类如图 1所示,移动副在前而转动副在后,同时移动特征影响转动中心O位置发生变化,即${{G}_{F}}^{I}({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})$;反之第2类如图 2所示,转动副在前而移动副在后,移动特征的变化不影响转动中心O的位置即${{G}_{F}}^{Ⅱ}({{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }};\text{ }{{T}_{a}}~{{T}_{b}}~0)$
|
图 1 GFI第1类 |
|
图 2 GFⅡ第类 |
串联机器人末端特征依赖组成该机构所有运动副的特征的总和,即GF 集求和运算:
| $\begin{align} & {{G}_{F1}}=\left( A;\text{ }B \right)=({{T}_{a1}}~{{T}_{b1}}~{{T}_{c1}};\text{ }{{R}_{\alpha 1}}~{{R}_{\beta 1}}~{{R}_{\gamma 1}}), \\ & {{G}_{F2}}=\left( C;\text{ }D \right)=({{T}_{a2}}~{{T}_{b2}}~{{T}_{c2}};\text{ }{{R}_{\alpha 2}}~{{R}_{\beta 2}}~{{R}_{\gamma 2}}), \\ \end{align}$ |
则
| ${{G}_{F}}={{G}_{F1}}\cup {{G}_{F2}}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})\text{ },$ | (1) |
| $\begin{align} & ({{T}_{a}}~{{T}_{b}}~{{T}_{c}})=A\cup C\cup T\left( A+B \right)\cup \left. \left( C+D \right) \right), \\ & ({{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})=R\left( A+B \right)\cup \left. \left( C+D \right) \right). \\ \end{align}$ |
式中: “∪”为求和运算,“+”为Ti对Rj的影响运算符,其遵循轴线迁移定理[15],T(·)为移动特征部分,R(·)为转动特征部分.
并联机构的运动特征是构成并联机构的多条支链运动特征的交集,即
| ${{G}_{F}}={{G}_{F1}}\cap \text{ }{{G}_{F2}}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})\text{ },$ | (2) |
| $\begin{align} & ({{T}_{a}}~{{T}_{b}}~{{T}_{c}})=A\cap C, \\ & ({{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})=R\left( A+B \right)\cap \left( C+D \right). \\ \end{align}$ |
式中“∩”为求交运算符.
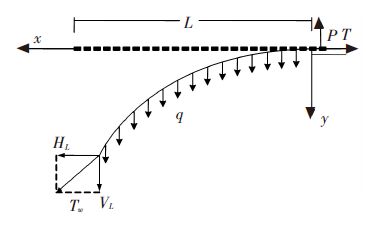
由式(2)很容易判断移动特征Ti,而转动特征Rj的确定比较困难,如图 3所示,平台任意两点Ao、Bo,当刚体绕Ao点旋转时,点Bo到达B点.由坐标变换位移矩阵可知:
| $\left\{ \matrix{ \left[ B \right] = [{R_{\alpha ,\beta ,\gamma }}][{R_o} - {A_o}\left] + \right[A], \hfill \cr \left[ \matrix{ B \hfill \cr 1 \hfill \cr} \right] = \left[ \matrix{ {R_{\alpha ,\beta ,\gamma }}{R_{\alpha ,\beta ,\gamma }}\left[ { - {A_o}} \right] + \hfill \cr 01 \hfill \cr} \right]\left[ \matrix{ {B_o} \hfill \cr 1 \hfill \cr} \right] \hfill \cr} \right..$ | (3) |
|
图 3 两点间三维相对转动的关系 |
式中: [Ao]、[Bo]分别表示刚体上两点起始位置;[A]、[B]分别变化后的位置; [Rα,β,γ]为三维矩阵,是刚体绕A点的转动变换.
由式(3)可知,VB不仅具有VA相同的转动,而且B点具有三维伴随移动,即
| $\begin{align} & {{G}^{}}_{FA}=({{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }};\text{ }0\text{ }0\text{ }0), \\ & {{G}^{}}_{FB}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }}), \\ & {{G}^{}}_{FA}\cap {{G}^{}}_{FB}=({{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }};\text{ }0\text{ }0\text{ }0). \\ \end{align}$ |
同理可知,当 [Rα,β,γ]变为[Rα,β]及[Rα]时的B点运动特征,在此给出转动特征合成定律:如果机构绕点A旋转,则机构上任意点B有与点A相同的转动,同时B点还存在绕点A转动的伴随移动.
式(1)、(2)为机构综合的理论基础,而轴线迁移定理、转动合成定律为求和、求交运算的依据.
2 完全各向同性解耦并联机构型综合Gogu[16]将运动雅克比矩阵是对角矩阵且对角元素相等的并联机构定义为完全各向同性.金琼[17]基于输入输出矩阵给出完全解耦定义,即:输入与输出变量存在一一对应关系.由此看出“完全解耦”包括了“完全各向同性”.
完全各向同性并联机构设计主要是支链的设计和输入运动副的选择.为了使机构具有某个方向的解耦输入,在此约定并联机构运动特征
Zeng等[5]对于解耦并联机构设计一般都是先给出分支型综合准则,然后给出输入运动副的选择原则,但是,这种方法使得输入运动副的选择变得复杂.
为了简化输入运动副的选择,由公式并联机构数综合方程
| $\left\{ \begin{align} & F-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{q}_{i}}=0\text{ }, \\ & N=F-\underset{i=1}{\overset{n}{\mathop{\sum }}}\,({{q}_{i}}-1)+p, \\ & N=n+p \\ \end{align} \right.$ | (4) |
可知,当p=0,qi=1时,F=N=n.
式中:F为机构维数,N为支链数,n为具有主动支链数,qi为主动支链i上的驱动数,p为被动支链数.
在此给出完全各向同性并联机构输入运动副选择原则:
1) 并联机构末端运动GF 集中所有元素均为并联机构输入运动;
2) 每个支链均只有一个输入运动副,且支链中输入运动副与并联机构GF 集中某个特征元素相对应,移动特征对应移动副,转动特征对应转动副.
2.2 完全各向同性支链型综合准则支链设计准则:当已知支链运动特征 GFi时,首先确定该分支输入运动副,当输入运动特征为Ti,则输入运动副为移动副,该分支中的其余移动特征方向只能与Ti垂直,若分支中存在轴线平行的转动副,其轴线方向只能平行于Ti;当输入运动特征为Rj,则输入运动副为转动副,该支链中其余转动副或圆柱副的轴线垂直于Rj轴线.
考虑完全各向同性并联机构的设计减弱了机构的刚性,各支链的设计中尽可能地使用复合运动副,输入运动副尽量靠近平台.
2.3 完全各向同性解耦并联机构型综合步骤1) 将给定并联机构的运动特征,用GF集表示.例如两移两转四自由度并联机构末端
2) 根据并联机构GF表达式,首先按照公式(3)确定并联机构各分支GFi集,然后按照输入运动副选择原则确定并联机构各支链驱动;
3) 将支链GiF集根据公式(2)和遵循并联分支解耦设计准则构造并联解耦分支;
4) 将从3)得到的解耦分支按照公式(3)布置各分支位置组成闭环解耦并联机构.
3 完全各向同性2T2R并联机构型综合根据上述完全各向同性并联机构型综合方法, 对2T2R并联机构进行构型设计,其运动特征为
| ${{G}_{F}}^{I}=({{T}_{a}}~0\text{ }{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0)$ |
设Ta、Tc为沿X、Z轴方向的移动特征,Rα、Rβ为绕平行于X、Y轴的转动特征.由式(4)可知:
| $p=0,{{q}_{i}}=1时F=N=n=4$ |
该并联机构由4条支链组成,依据式(2)交集运算可得可能支链 GFi集为
| ${{G}^{}}_{~Fi}=({{T}_{a}}~0\text{ }{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0),$ | (5) |
| ${{G}^{}}_{~Fi}=({{T}_{a}}~0\text{ }{{T}_{c}}\text{; }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }}),$ | (6) |
| ${{G}^{}}_{~Fi}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0),$ | (7) |
| ${{G}^{}}_{~Fi}=({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~{{R}_{\gamma }})\text{ }.$ | (8) |
式(5)~(8)分别简写为
| 表 1 GFI(Ta 0 Tc; Rα Rβ 0)的组合方式 |
根据驱动运动副选择原则,设分支1、2中驱动副为移动副,分支3、4中驱动副为转动副.然后按照支链解耦准则分别构造 2T2R、2T3R、3T3R支链,如表 2~5所示.
| 表 2 G2T2RFi型串联分支构型 |
表 2中 UYX为平行于Y、X轴线的万向铰.CX为线性输入,下标字母X、Y、Z表示运动副的移动方向或转动副的轴线方向,当组合方式中存在两个2T2R分支时,另一分支中的驱动副为PZ、CZ,此时只需将下标X、Z相互替换.
从表 1支链组合方式中可知,必定存在两个 2T3R支链,表 3给出了驱动副为PX.当第二个分支为2T3R支链,此时驱动副为PZ,其支链类型只需将下标X、Z相互替换.
| 表 3 G2T3RFi型串联分支构型 Table 3 英文标题 |
表 4中 PZa表示平行四边形铰链平行于Z轴,XU^表示转平万向铰中转动副轴线平行于X轴,U*为纯平动万向铰[18],CX为线性输入.由表 1可知G3T2RFi分支可以为分支2、3,故表 4中给出驱动副为移动副和转动副的情况.当RY为驱动运动副时只需将表 4中驱动副RX的支链类型下标X、Y相互替换.
| 表 4 G3T2RFi型串联分支构型 |
表 5中 UP表示平面移动万向铰[18],CY为转动特征输入.由表 1组合方式可知G3T3RFi分支以转动特征为输入驱动,若驱动副为RX或CX时,将表 5支链类型下标X、Y相互替换.
| 表 5 G3T3RFi型串联分支构型 |
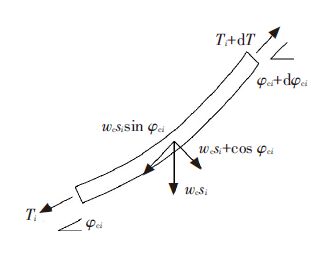
最后,按照表 1中分支组合方式分别在表 2~5中各选取一个支链类型,组合成四分支闭环完全解耦并联机构.以表 1中组合方式(4)为例,设4个支链驱动副依次为PX、PZ、RY、RX,根据驱动副分别选取表 2中PXPZRXRY为支链1,表 4中PZPXCYRX为支链2,PXPXaRXRXRY为支链3,表 5中RYRYRZRZRZRX为支链4,构成如图(4)所示完全解耦并联机构.
图 4中以支链1、3为例,运用GF集运算法则对其验证分析.其中,支链3由1个移动副PX、1个平行四边形铰链PXa、两个平行X轴的转动副RX、1个平行Y轴的转动副RY组成,由于转动副RX垂直于PXaRX形成的YZ移动平面,故PXaRXRX满足轴线迁移定理,可表示为
| ${{G}_{F}}^{I}=(0\text{ }{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~0\text{ }0),$ |
|
图 4 完全各向同性解耦2T2R并联机构 |
由式(1)可得
| $\begin{align} & {{G}^{I}}_{F3}=G\left( {{P}_{X}} \right)\cup G\left[ {{P}^{X}}_{a}{{R}_{X}}{{R}_{X}} \right]\cup G\left[ {{R}_{Y}} \right]= \\ & ({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0). \\ \end{align}$ | (9) |
式(9)中 G(·) 表示运动关节运动特征.
同理可知支链1为
| ${{G}^{I}}_{F1}=({{T}_{a}}~0\text{ }{{T}_{c}}\text{; }{{R}_{\alpha }}~{{R}_{\beta }}~0).$ |
当支链1、3转动特征求交时,由图 4可知, 两支链中均包含平行X、Y轴线的转动副,同时支链3中存在三维移动特征,由转动合成定律可知存在平行于X、Y轴线的转动特征.由式(2)可得
| $\begin{align} & {{G}_{F}}^{I}={{G}_{F1}}^{I}\cap {{G}_{F3}}^{I}= \\ & ({{T}_{a}}~{{T}_{b}}~{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0)\cap ({{T}_{a}}~0\text{ }{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0)= \\ & ({{T}_{a}}~0\text{ }{{T}_{c}};\text{ }{{R}_{\alpha }}~{{R}_{\beta }}~0)\text{ }. \\ \end{align}$ | (10) |
|
图 5 完全各向同性解耦2T2R并联机构螺旋系 |
由式(10)可知支链1、3求交其结果为两移动两转动运动特征.
4 机构自由度和速度分析 4.1 机构自由度分析如图(5)所示, 定坐标系OXYZ原点位于定平台中心位置,设3个分支坐标系分别为o1x1y1z1、o2x2y2z2、o3x3y3z3.
根据图(5)所建立的坐标系,支链1的运动螺旋为
| $\begin{align} & {{\$}_{11}}=\left( 0,0,0;\text{ }1,0,0 \right), \\ & {{\$}_{12}}=\left( 0,0,0;\text{ }0,0,1 \right), \\ & {{\$}_{13}}=\left( 1,0,0;\text{ }0,0,0 \right), \\ & {{\$}_{14}}=\left( 0,1,0;\text{ }0,0,0 \right), \\ \end{align}$ | (11) |
由式(11)的运动螺旋可得约束螺旋系为
| $\begin{align} & {{\$}^{r}}_{11}=\left( 0,1,0;\text{ }0,0,0 \right), \\ & {{\$}^{r}}_{12}=\left( 0,0,0;\text{ }0,0,1 \right). \\ \end{align}$ | (12) |
式(12) 表示一个约束力约束了动平台沿 Y 轴方向移动和一个力偶限制了绕Z轴方向的转动.
支链2运动螺旋系为
| $\begin{align} & {{\$}_{21}}=\left( 0,0,0;\text{ }0,0,1 \right), \\ & {{\$}_{22}}=\left( 0,0,0;\text{ }1,0,0 \right)\text{ }, \\ & {{\$}_{23}}=\left( 0,1,0;\text{ }0,1,0 \right)\text{ }, \\ & {{\$}_{24}}=(1,0,0;\text{ }0,{{b}_{3}},{{c}_{3}}).~ \\ \end{align}$ | (13) |
由式(13)可得支链2的约束螺旋为
| ${{\$}^{r}}_{21}=\left( 0,0,0;\text{ }0,0,1 \right).$ | (14) |
式(14) 表示1个力偶限制了绕Z轴方向的转动.
支链3中存在1个复合铰链,可以当做1个整体,其运动螺旋系为
| $\begin{align} & {{\$}_{3}}_{1}=\left( 0,0,0;\text{ }1,0,0 \right), \\ & {{\$}_{3}}_{2}=(0,0,0;\text{ }{{a}_{3}},{{b}_{3}},0), \\ & {{\$}_{33}}=(1,0,0;\text{ }0,{{b}_{4}},{{c}_{4}}), \\ & {{\$}_{3}}_{4}=\left( 1,0,0;\text{ }0,0,0 \right)\text{ }, \\ & {{\$}_{3}}_{5}=\left( 0,1,0;\text{ }0,0,0 \right)\text{ }. \\ \end{align}$ | (15) |
由式(15)可得支链3的约束螺旋为
| ${{\$}^{r}}_{21}=\left( 0,0,0;\text{ }0,0,1 \right).$ | (16) |
式(16)表示一个力偶限制了绕Z轴方向的转动.
由于支链4为无冗余六自由度的运动链, 故对动平台无约束,从上述约束螺旋可知,4个支链共同作用了一个力线失和一个力偶,约束了机构沿Y轴方向的移动和绕Z轴的转动,且机构过约束v=2.根据文献[19]计算机构自由度:
| $\begin{align} & F=d\left( n-g-1 \right)+\sum gi=1{{f}_{i}}+v+\xi = \\ & 6\left( 17-19-1 \right)+20+2=4. \\ \end{align}$ |
式中:F为机构自由度,d为机构阶数,n为构件数,g为运动副数,fi为第i个运动副自由度,v为过约束数,ξ为局部自由度.
4.2 机构速度分析图 6所示4个支链与动平台连接的转动副轴线相交于 O1,设点O1为动坐标系原点,定平台上点O2为点O1的投影,点O为定坐标系原点,动平台与定平台的距离为h.
|
图 6 机构运动参数 |
由输入运动副选择原则可得输入运动, 对应的运动参数为:支链1输入为沿定坐标系X方向发生位移L,支链2输入为沿惯性坐标系Z方向发生位移H,支链3输入为绕平行于Y轴转动角度ψ,支链4输入为绕平行于X轴转动角度φ.输出参数为动坐标系X轴的转动角度α,动坐标系Y轴的转动角度β,动坐标系原点O1在定坐标系下的坐标为(l,0,h0).
设定坐标系、动坐标系各轴对应平行为机构初时位姿,动坐标系原点O1在定坐标系下的坐标为(l0,0,h0),φ=0,ψ=0.
机构位置正解即为已知输入量(L,H,φ,ψ),求解输出量(l,h,α,β).由图 6可知,支链1的X向移动输入通过一个沿Z向移动和两个转动副带动动平台发生移动Z向移动,在该分支中有且仅有一个改方向的移动.支链2中移动输入通过带动3个连杆使得机构动平台发生移动,故有
| $\left\{ \begin{align} & l={{l}_{o}}+L, \\ & h={{h}_{o}}+H. \\ \end{align} \right.$ | (17) |
支链3中转动副轴线始终与动坐标系的 Y轴平行,支链4转动副轴线始终与动坐标系的X轴平行,故有
| $\left\{ \begin{align} & \alpha =\varphi , \\ & \beta =\psi . \\ \end{align} \right.$ | (18) |
并联机构末端的速度和输入驱动的速度关系为
| $\dot{X}=J\dot{q}$ |
式中: 为机构的速度,为各输入速度,J为雅克比矩阵,描述了机构的输入与输出速度间的映射关系.
对式(17)、(18)两边求导,可得
| $\left\{ \begin{align} & \dot{l}=\dot{L}, \\ & \dot{h}=\dot{H}, \\ & \dot{\beta }=\dot{\psi }, \\ & \dot{\alpha }=\dot{\varphi }, \\ \end{align} \right.$ | (19) |
式(19)以矩阵形式表示为
| $\left[ \matrix{ 1{\rm{ }}0{\rm{ }}0{\rm{ }}0 \hfill \cr 0{\rm{ }}1{\rm{ }}0{\rm{ }}0 \hfill \cr 0{\rm{ }}0{\rm{ }}1{\rm{ }}0 \hfill \cr 0{\rm{ }}0{\rm{ }}0{\rm{ }}1 \hfill \cr} \right].\left[ \matrix{ {\dot L} \hfill \cr {\dot H} \hfill \cr {\dot \psi } \hfill \cr {\dot \varphi } \hfill \cr} \right] = \left[ \matrix{ {\dot l} \hfill \cr {\dot h} \hfill \cr {\dot \beta } \hfill \cr {\dot \alpha } \hfill \cr} \right]$ | (20) |
令
| $M=\left[ \begin{align} & 10000 \\ & 10000 \\ & 100001 \\ \end{align} \right],$ |
式(20)可整理为
| $\left[ \matrix{ {\dot L} \hfill \cr {\dot H} \hfill \cr {\dot \varphi } \hfill \cr {\dot \psi } \hfill \cr} \right] = {M^{ - 1}}{\rm{ }}\left[ \matrix{ {\dot l} \hfill \cr {\dot h} \hfill \cr {\dot \beta } \hfill \cr {\dot \alpha } \hfill \cr} \right],J = {M^{ - 1}} = \left[ \matrix{ 1{\rm{ }}0{\rm{ }}0{\rm{ }}0 \hfill \cr 0{\rm{ }}1{\rm{ }}0{\rm{ }}0 \hfill \cr 0{\rm{ }}0{\rm{ }}1{\rm{ }}0 \hfill \cr 0{\rm{ }}0{\rm{ }}0{\rm{ }}1 \hfill \cr} \right].$ |
可见,该机构的雅克比矩阵J为单位矩阵,表明该2T2R并联机构具有完全各向同性.
5 结论1) 本文基于GF集构型理论,提出了一种完全各向同性并联机构型综合方法,该方法给出了输入运动副选择原则,支链构型准则以及完全各向同性并联机构设计的步骤.
2) 运用该型综合方法,综合出大量新型完全各向同性四自由度2T2R并联机构.
3) 基于螺旋理论求解了构造出的一种机构的运动特征,同时求得机构的雅克比矩阵,验证了并联机构的完全各向同性及解耦性,证明了构型理论正确性.
4) 该综合方法可用于具有良好的运动学和力传递性能并联机构的构型设计,对机构构型综合具有一定的指导作用.
| [1] |
HUANG Zhen, LI Qinchuan. General methodology for type synthesis of lower-mobility symmetrical parallel manipulators and several novel manipulators[J].
International Journal of Robotics Research,2002, 21 (2) : 131-145.
( 0) 0)
|
| [2] |
LI Qinchuan, HUANG Zhen, HERV J M. Displacement manifold method for type synthesis of lower-mobility parallel mechanisms[J].
Science in China Series E: Technological Sciences,2004, 47 (6) : 641-650.
( 0) 0)
|
| [3] |
YANG Tingli, LIU Anxin, JIN Qiong, et al. Position and orientation characteristic equation for topological design of robot mechanisms[J].
Journal of Mechanical Design,2009, 131 (2) : 1-12.
( 0) 0)
|
| [4] |
YANG Jialun, GAO Feng, GE Q J, et al. Type synthesis of parallel mechanisms having the first class GF sets and one-dimensional rotation[J].
Robotica,2011, 29 (6) : 895-902.
( 0) 0)
|
| [5] |
ZENG Daxing, HOU Yulei, LU Wenjuan, et al. Comparative analysis of characteristics of the coupled and decoupled parallel mechanisms[J].
Chinese Journal Mechanical Engineering,2010, 23 (4) : 468-476.
( 0) 0)
|
| [6] |
KONG X W, GOSSELIN C M. Type synthesis of input-output decoupled parallel manipulators[J].
Transactions of the Canadian Society for Mechanical Engineering,2004, 28 (2 A) : 185-196.
( 0) 0)
|
| [7] |
ZENG Daxing, HUANG Zhen. Type synthesis of the rotational decoupled parallel mechanism based on screw theory[J].
Science China technological Sciences,2011, 54 (4) : 998-1004.
( 0) 0)
|
| [8] |
GOGU G. Structural synthesis of fully-isotropic translational parallel robots via theory of linear transformations[J].
European Journal of Mechanics-A/Solids,2004, 23 (6) : 1021-1039.
( 0) 0)
|
| [9] |
ZHANG Yanbin, LIU Hongzhao, WU Xin. Kinematics analysis of a novel parallel manipulator[J].
Mechanism and Machine Theory,2009, 44 (9) : 1648-1657.
( 0) 0)
|
| [10] |
XIE Fugui, LIU Xinjun, WANG Liping, et al. Optimal design and development of a decoupled A/B-axis tool head with parallel kinematics[J].
Advances in Mechanical Engineering,2010, 210 (1) : 1-14.
( 0) 0)
|
| [11] |
陈修祥, 马履中, 吴伟光, 等. 两平移两转动多自由度减振平台设计与试验[J].
农业机械学报,2007, 38 (9) : 122-125.
( 0) 0)
|
| [12] |
刘剑敏, 马履中, 许子红, 等. 振动筛两平移两转动并联机构的运动学分析[J].
农业机械学报,2008, 39 (2) : 59-62.
( 0) 0)
|
| [13] |
GOGU G. Fully-isotropic parallel robots with four degrees of freedom T2R2-type[C]//Proceedings of International Conference on Intelligent Robots and Systems (IROS 2005). Edmonton: IEEE, 2005: 1190-1195.
( 0) 0)
|
| [14] |
张彦斌, 吴鑫. 完全解耦二移动二转动并联机构结构综合[J].
农业机械学报,2013, 44 (8) : 250-256.
( 0) 0)
|
| [15] |
高峰, 杨加伦, 葛巧德.
并联机器人型综合的GF集理论[M]. 北京: 科学出版社, 2011 : 43 -47.
( 0) 0)
|
| [16] |
GOGU G. Structural synthesis of fully-isotropic parallel robots with Sch nflies motions via theory of linear transformations and evolutionary morphology[J].
European Journal of Mechanics-A/Solids,2007, 26 (2) : 242-269.
( 0) 0)
|
| [17] |
金琼. 过约束机构与欠秩并联机器人机构研究[D]. 南京: 东南大学, 2001: 100-120.
( 0) 0)
|
| [18] |
GAO Feng, LI Weimin, ZHAO Xianchao, et al. New kinematic structures for 2-, 3-, 4-, and 5-DoF parallel manipulator designs[J].
Mechanism and Machine Theory,2002, 37 (12) : 1395-1411.
( 0) 0)
|
| [19] |
黄真, 赵永生, 赵铁石.
高等空间机构学[M]. 北京: 中国高等教育出版社, 2006 : 117 -121.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


