2. 哈尔滨理工大学 电气与电子工程学院, 哈尔滨 150080 ;
3. 哈尔滨工业大学 经济与管理学院, 哈尔滨 150001 ;
4. 水力发电设备国家重点实验室(哈尔滨大电机研究所), 哈尔滨 150040
2. School of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China ;
3. School of Management, Harbin Institute of Technology, Harbin 150001, China ;
4. State Key Laboratory of Hydropower Equipment(Harbin Institute of Large Electrical Machinery), Harbin 150040, China
长期以来,人们一直关注水轮机内部流动的复杂非线性行为,力求通过对流动非线性特性的研究,揭示流体运动的动力学现象和规律,及时诊断和控制可能的运行故障,为水轮机的安全稳定运行提供理论依据[1]. 水轮机正常运行时,内部流场的压力脉动和速度脉动信号均呈现比较明显的叠加周期性;偏离最优工况时,出现非准周期的脉动信号[2-6]. 水轮机在偏工况,且由轻微空化演变到严重空化或者出现故障时,脉动信号具有混乱、瞬变的特征,因此可利用混沌理论来对信号进行定量分析.
目前,在水轮机调速系统和故障预测混沌特性方面已经开展了一些研究. 杨锋等[7]利用混沌理论和数字仿真方法研究了水轮发电机组调速系统的转速控制问题,讨论了控制参数对水轮发电机组调速系统出现混沌现象的影响;凌代俭等[8]利用混沌动力学理论对水轮机调节系统中的复杂非线性动力学现象和稳定性进行了分析;陈帝伊等[9]利用混沌理论研究了水轮机调速器运行的参数特征,并利用滑模变结构控制方法有效地改善水轮机调速器的动态特性;程宝清等[10]提出将小波频带分析与灰色预测理论相结合的方法来进行水电机组故障预测. 近年来混沌理论也引入到了水轮调速系统中[11],尤其是甩负荷过程的动力学变化系统中[12]. 上述研究是针对水轮机调节系统等对象来研究的,然而也间接说明了水轮机内部的空化流动也相应呈混沌流态. 针对混沌理论在湍流场中的应用,宁伟征等[13]对于偏心射流强化流体混合的流场进行了混沌动力学分析,发现偏心射流流场包含混沌混合区和混合隔离区,其中混沌混合区内流体运动轨迹较复杂,Lyapunov指数规律被拉伸,混合程度最高.
为更好地了解水轮机内部流场的不稳定特性,解决目前水轮机空化故障难以诊断的问题,本文首次利用混沌动力学方法对水轮机在偏工况运行时的压力脉动进行研究. 针对从轻度空化到严重空化变化的工况过程,分析脉动信号的时域图、时频图、相图、最大Lyapunov指数及Poincaré映射图,研究混沌特性的演变过程,以此完成对水轮机的运行监测,实现快速的故障诊断.
1 水轮机内部不稳定流动及尾水管压力脉动为准确地反映水轮机的内部流动特性及不稳定流动时的脉动信号,进行了水轮机模型实验,实时采集水轮机流场诱发的压力脉动信号. 实验中选取混流式模型转轮,比转速287,进出口直径分别为360 mm和353 mm,测试最高水头71 m,最低水头44 m. 根据其综合特性,转轮最高效率点(94.47%)位于活动导叶开度线a=16 mm上,沿着该导叶开度线,偏离最高效率点的设计工况时,将在水轮机内部形成不同的空化状态. 偏工况运行时,会在转轮区和尾水管区均形成空化带,此时会引起内部流动强烈振荡变化,速度脉动和压力脉动显著. 参考IEC60193测试标准,并依据客户提出的测试要求,在尾水管壁面上布置了4个压力测点:即尾水锥管上游有两个测点(转轮下方0.32 D处)draft1和draft2,肘管处内外侧各一个测点(转轮下方1.02 D处)draft3和draft4,如图 1所示.
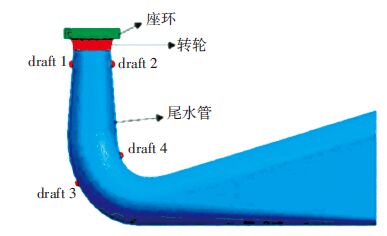
|
图 1 压力脉动测点布置位置 |
在封闭循环的实验台上进行水轮机特性实验,在转轮同轴上配有测功机系统,所以系统中的流量和转轮转速都是可控的,配合进口调节流量阀和测功机,可以使系统运行在指定的工况点. 相应工况点的参数包括:导叶开度a(mm)、单位转速n11(r/min)、装置空化数σ. 其中,σ值越大,说明系统抗空化的性能越好. 实验时,先将系统调节至最优工况,即a=16 mm,n11=74.5 r/min,σ值最大,进行压力信号采集;然后,通过调节尾水管后方密闭水箱中的真空度改变系统内部的空化压力,使转轮达到不同的空化数,调节σ值后进行压力信号再次测量;再将系统沿导叶开度线调节至偏工况运行,并配合调节σ值后,进行下一次测量. 从轻度空化到严重空化的变化过程中,采集压力检测点的脉动信号,脉动信号的采样频率为4 kHz.
1.1 尾水管内部流动在系统的尾水管部分,安装了内窥镜成像系统,从而可对转轮叶片背面脱流、叶道涡和尾水管涡带等进行观察. 选取几个典型的工况,覆盖了水轮机从轻微空化过渡到严重空化的状态,在这些工况下进行压力脉动实验,并记录不同运行条件下的尾水管内部流动特征,如图 2所示.

|
图 2 不同实验工况下尾水管中流动状态图 |
由图 2可知,从工况1~工况4,空化现象从无到有,尾水管涡带最后发展成空泡型涡带,表示系统已经发生较严重的空化.
1.2 压力脉动信号时域特征流体机械内部发生空化时,内部流场产生的压力脉动是复杂的非线性信号,监测点压力随时间变化剧烈. 由于信号监测中的环境噪声及测量误差会对压力脉动信号引入一定的噪声,为了准确地分析压力脉动信号的动力学特征,需要对原始压力脉动信号进行去噪处理. 本文利用提升小波变换方法针对肘管外侧draft3监测点的压力脉动信号进行降噪处理,处理前后信号的时域图形如图 3所示.

|
图 3 工况3原始信号与小波去噪后信号的时域波形图 |
由图 3可知,由于原信号含有复杂的加性噪声或者乘性噪声,利用小波提升技术去噪后,去噪后的信号很好地保持了原始信号的特征,信号变得干净,可用于动力学特征的研究和探讨.
2 混沌动力学特性 2.1 时频能量分布水轮机入口压力脉动信号属于瞬变信号,其频域特征随着空化程度的变化产生突发和畸变,是一种典型的非平稳信号. 针对这种非平稳信号,利用小波去噪后的水轮机压力脉动信号,使用短时Fourier变换对工况3进行时频联合分析,结果见图 4所示.

|
图 4 工况3的压力脉动信号时频分布 |
由图 4可知,肘管外侧的压力脉动信号是频率分布广泛的脉动信号,能量主要集中在低频段,最大值分布范围低于0.4 kHz,之后在整个频率范围衰减,故水轮机气蚀程度受低频段脉动影响最大,由图 3可初步判断水轮机压力脉动信号的频带分布.
2.2 相轨迹分析在相空间重构过程中,如果用x表示观测到的变量分量x(t),t = 1,2,…,N,重构相空间需根据嵌入维数m得到一组新向量序列
| $X\left( t \right)\text{ }=\text{ }{{\left\{ x\left( t \right),x\left( t+\tau \right),\ldots ,x\left[ t+\text{ }\left( m-\text{ }1 \right)\tau \right] \right\}}^{T}}$ |
| $t=\text{ }1,2,\ldots ,M$ |
其中:M = N - (m - 1)τ,τ为时间延迟,通常τ要选得比激励周期小得多,在相空间重构中关键是找到合适的τ,使得原序列x(t)与x(t + τ)不是线性相关. 这个由观测值及其延时值所构成的m维状态空间即为重构的相空间,它与原始的状态空间是微分同肧的. 可以根据相轨迹图的收缩或扩张趋势,判断水轮机内部流动空化程度的强弱. 图 5给出空化数较大的工况3与工况4的压力脉动相轨迹图.

|
图 5 工况3与工况4的压力脉动相轨迹分布图 |
由图 5可知,工况3与工况4偏离设计工况,相轨迹离散明显,随着装置空化数减小,空化程度增强,机组的振动和噪声加大,吸引子的离散程度增大,表明压力脉动信号混沌程度严重.
2.3 Poincaré映射图分析在相空间中选取适当的利于观察系统运动特征和变化的截面(截面不与轨迹线相切,不包含轨迹线),此截面上某一对共轭变量取固定值,称此截面为Poincaré截面,Poincaré截面也是判断系统是否处于混沌状态的一个标志. 相空间的连续轨迹与Poincaré截面的交点称为截点,如果截点数目有限,则可判断系统处于周期运动,如果截点数目无限或者呈现云图形状,则可判断系统处于混沌运动状态,因此图 3可通过观察Poincaré截面上截点的情况判断系统是否发生混沌. 相应工况下的Poincare截面图如图 6所示.

|
图 6 不同工况下的Poincaré截面 |
由图 6可知,图(a)与图(b)中设计的装置空化数较小,Poincare截面上的点分布比较集中,表明内部流动混乱程度不大,属于轻微空化. 图(c)与图(d)中设计的装置空化数较大,Poincare截面上的离散点数分布比较分散,成片状分布,具有明显的混沌特征. 即,图 6中4幅图表明在无空化、轻微空化或严重空化时,Poincaré截面图上的点分散于不同区域,随着空化程度的加重,Poincaré截面上的点变得更加离散,表明混沌程度加重.
2.4 Lyapunov指数分析为定量分析空化或故障时的压力脉动信号,可采用Lyapunov指数判别其混沌程度. 基于相空间重构的数据,可利用小数据量方法获取Lyapunov指数. 本文Lyapunov指数的计算步骤如下:对水轮机压力脉动时间序列x(t)进行FFT变换,计算序列的平均周期p;用C-C算法计算序列嵌入维数m和延迟时间τ,并重构相空间x(t);在相空间中任意选定一点x(t),在其附近寻找最近邻点x(t)′,用时间序列的平均周期p限制相空间点中最临近点dt(0)的短暂分离;对相空间中任意选定的一点x(t),计算第t对最邻近点经过i个离散步长的距离dt(i);根据Sato估计dt(i)与dt(0)之间的关系dt(i)=dt(0)e1λ(iΔt)(其中,Δt为观测时间序列的步长);对上面近似关系的两边取对数得ln dt(i)的关系;对于每个点i求出所有t的ln dt(i)取平均值,即得到y(i),然后利用最小二乘法拟合做出回归直线,该直线的斜率是时间序列的最大Lyapunov指数.
仿真参数:嵌入维数m=3,时延τ=9,截取相空间重构的4 500点数据进行计算,获得序列所选数据点数i与y(i)的关系曲线如图 7所示.

|
图 7 数据点数i与y(i)关系曲线 |
图 7中,通过计算得到工况1~4的最大Lyapunov指数分别为0.021 5、0.024 8、0.031 6和0.033 9. 可知水轮机信号在轻微空化发展到严重空化的过程中,动力学特征存在明显差异. 对比图 2中尾水管空化涡带发展的形态,空化逐渐增强后,反映为Lyapunov指数逐渐增大,由此可以根据数据处理获得的Lyapunov指数大小来远程监测压力脉动信号,并判别水轮机运行状态.
3 结 论1) 随着空化程度的加重,时域信号杂乱无章程度逐渐增强;
2) 压力脉动信号的主要成分在低频段,随着空化程度的加重,低频段信号的能量整体水平都有所提高,相图呈现杂乱无章的状态,Poincare截面呈现片状分布,最大Lyapunov指数增大,且大于零.
| [1] |
郑源, 李玲玉, 周大庆, 等. 微水头灯泡贯流式水轮机支撑及导叶联合设计[J].
华中科技大学学报(自然科学版),2014, 42 (9) : 128-132.
( 0) 0)
|
| [2] |
苏文涛. 大型混流式水轮机模型内部流动稳定性研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
( 0) 0)
|
| [3] |
李章超, 常近时, 辛喆. 射水减弱混流式水轮机尾水管内压力脉动的数值模拟[J].
农业机械学报,2013, 44 (1) : 53-57.
( 0) 0)
|
| [4] |
季斌, 罗先武, 西道弘, 等. 混流式水轮机涡带工况下两级动静干涉及其压力脉动传播特性分析[J].
水力发电学报,2014, 33 (1) : 191-196.
( 0) 0)
|
| [5] |
桂中华, 常玉红, 柴小龙, 等. 混流式水轮机压力脉动与振动稳定性研究进展[J].
大电机技术,2014 (6) : 61-65.
( 0) 0)
|
| [6] |
李万, 钱忠东, 郜元勇. 4种湍流模型对混流式水轮机压力脉动模拟的比较[J].
武汉大学学报(工学版),2013, 46 (2) : 174-179.
( 0) 0)
|
| [7] |
杨锋, 栾国森, 邓长虹. 水轮机调速系统的混沌特征—控制器参数的影响[J].
武汉水利电力大学(宜昌)学报,1999, 21 (3) : 230-234.
( 0) 0)
|
| [8] |
凌代俭. 水轮机调节系统分岔与混沌特性的研究 [D]. 南京: 河海大学, 2007.
( 0) 0)
|
| [9] |
陈帝伊, 杨朋超, 马孝义, 等. 水轮机调节系统的混沌现象分析及控制[J].
中国电机工程学报,2011, 31 (14) : 113-120.
( 0) 0)
|
| [10] |
程宝清, 韩凤琴, 桂中华. 基于小波的灰色预测理论在水电机组故障预测中的应用[J].
电网技术,2005, 29 (13) : 40-44.
( 0) 0)
|
| [11] |
XU B, CHEN D, ZHANG H, et al. Modeling and stability analysis of a fractional-order Francis hydro-turbine governing system[J].
Chaos, Solitons & Fractals,2015, 75 : 50-61.
( 0) 0)
|
| [12] |
ZHANG H, CHEN D, XU B, et al. Nonlinear modeling and dynamic analysis of hydro-turbine governing system in the process of load rejection transient[J].
Energy Conversion and Management,2015, 90 : 128-137.
( 0) 0)
|
| [13] |
宁伟征. 偏心射流强化流体混沌混合的研究[D]. 重庆: 重庆大学, 2012.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


