对于深水海底管道铺设,管道受力及变形分析一直是铺管作业过程中关注的重点. 目前,对正常铺管与收、弃管作业研究居多,同时也涌现出了许多关于管道分析和计算的方法. 最早由Plunkett[1]对海底立管进行分析,并提出用奇异摄动法求解管道微分方程; Dareing等[2]首次将有限差分法应用管道微分方程的求解;Croll[3]首先提出对S型管道整体形态采用自然悬链线法进行分析计算,对微分方程求解过程进行简化,修正边界条件;Dixon等[4]考虑管道刚度,提出刚性悬链线法,并完成管道微分方程的求解;顾永宁[5]针对不同因素影响,分别提出了求解方法,对于刚性悬链线法,将只能应用于下弯段的刚性悬链线法拓展到上弯段,简化了计算;Kalliontzis[6]考虑了管道塑性变形对铺管作业的影响;随着有限元软件的兴起,Khdeir[7]提出采用ABAQUS对管道铺设静态进行分析. 迄今为止,对初始铺管作业过程研究较少,缺少对初始铺管过程中管道与缆索的静态与动态分析. 初始铺管作业是指海底管道在缆索的导引下从铺管船延伸至海床,同时张紧力逐渐增加至设计值的过程. 它是整个海上铺管作业的开始,是正常铺设的必要前提. 为达到仿真程序设计要求,对管道和缆索进行受力分析,针对数学模型实时解算方法进行研究是很有必要的. 而在初始铺管中,要求同时求出管道和缆索的形态,增加了求解的难度. 在初始铺管作业过程中,由于管道剪切变形和横截面的转动非常微小,因此其属于一种大变形梁[8].
本文以“海洋石油201”深水铺管起重船的初始铺管作业为研究对象,对初始铺管作业计算理论进行分析,在原有的铺管常用算法基础上提出了将非线性梁理论[9]应用于初始铺管计算,基于Euler-Bernoulli梁理论[10]建立了管道的初始铺设数学模型,并针对建立的微分方程特点,采用拟牛顿法[11-12]对方程组进行求解,利用迭代的方法求出微分方程边界,得出微分方程的数值解,从而解算出管道和缆索的形态和内力. 微分求积[13]数值算法,使微分方程求解精度高,计算量少,易于程序实现,更有利于视景仿真[14]系统对计算程序的需求. 建立起一套基于海洋石油201 船工程实践的视景仿真系统,不仅可以减少训练的危险性,缩短实船训练周期,还可以到达工程预演的目的,对提升作业效率与安全性,以及降低成本等有着积极重要的作用.
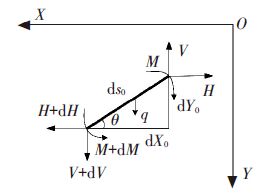
1 初始铺管微分方程 1.1 管道力学分析管线未变形前长度为L,直径为D,惯性矩为I,弹性模量为E,管线浮重度 (单位长度管线在水中的重量) w,在管线端部受到水平方向载荷H,竖直方向载荷V. 管线受力见图 1.
|
图 1 管线微段受力 |
图中θ=θ(x)为轴线的切线与x轴的夹角也是横截面的转角. 设弧长为s0=s0(x),由图 1可得如下几何关系:
| $\begin{align} & \text{d}{{s}_{0}}={{\left[ {{\left( \text{d}{{X}_{0}} \right)}^{2}}+{{\left( \text{d}{{Y}_{0}} \right)}^{2}} \right]}^{\frac{1}{2}}}=\delta \text{d}x, \\ & \frac{\text{d}{{X}_{0}}}{\text{d}{{s}_{0}}}=\text{cos}\theta ,\frac{\text{d}{{Y}_{0}}}{\text{d}{{s}_{0}}}=\text{sin}\theta , \\ & \frac{\text{d}M}{\text{d}{{s}_{0}}}=\text{cos}\theta ,\text{d}{{Y}_{0}}\text{d}{{s}_{0}}=\text{sin}\theta . \\ \end{align}$ |
其中δ为轴线伸长率.
由梁理论和胡克定律[15]可得
| $\begin{align} & M=-{{E}_{I}}\frac{\text{d}\theta }{\text{d}x},\frac{\text{d}V}{{{\text{d}}_{s0}}}=-w\text{ } \\ & \left( \delta -1 \right)={{T}_{W}}/{{E}_{A}}. \\ \end{align}$ |
其中:TW和M分别为轴力和弯矩,EA和EI分别为抗拉和抗弯刚度.
如图 3,管线变形后任意微分单元上有连续分布机械力q=w,利用内力等效关系,轴向内力TW (拉力为正)可表示为
| ${{T}_{W}}=Hcos\theta +Vsin\theta $ |
联立上式可以得到轴线伸长率和微分方程为
| $\begin{align} & \delta =1+\left( H\text{cos}\theta +V\text{sin}\theta \right)/{{E}_{\text{A}}} \\ & \frac{{{\text{d}}^{2}}\theta }{d{{x}^{2}}}=\left( V\text{cos}\theta -H\text{sin}\theta \right)/{{E}_{\text{I}}}. \\ \end{align}$ |

|
图 2 初始铺管示意 |

|
图 3 管线整体变形 |
从缆索中取出任意微段i,微段的受力情况如图 4所示,假设微段长度为si,两端的受力分别为Ti和Ti+dT,缆索自重简化为作用在微段重心上的集中力,在拉力和自重作用下缆索产生一定的转角dφci.

|
图 4 缆索单元受力 |
根据缆索微段轴向受力平衡,可以得到以下微分方程:
| $\begin{align} & \left( {{T}_{i}}+\text{d}T \right)\text{cos d}{{\varphi }_{ci}}={{w}_{c}}{{s}_{i}}\text{sin}{{\varphi }_{ci}}+{{T}_{i}}, \\ & \left( {{T}_{i}}+\text{d}T \right)\text{sin d}{{\varphi }_{ci}}={{w}_{c}}{{s}_{i}}\text{cos}{{\varphi }_{ci}}. \\ \end{align}$ |
式中:wc为缆索的浮重度,φc为缆索轴线与水平方向的夹角.
如果忽略缆索在轴向上的伸长量,将缆索分为n段,设由第i点至第i+1点的长度为si,两端的轴力分别为Ti和Ti+1,将上式写为线性积分形式为:
| $\begin{align} & {{T}_{i+1}}=\sqrt{{{\left( {{T}_{i}}+{{w}_{c}}{{s}_{i}}\text{sin}{{\varphi }_{ci}} \right)}^{2}}+{{\left( {{w}_{c}}{{s}_{i}}\text{cos}{{\varphi }_{ci}} \right)}^{2}}}, \\ & {{\varphi }_{ci+1}}={{\varphi }_{ci}}+\text{d}{{\varphi }_{ci}}={{\varphi }_{ci}}+\frac{{{w}_{c}}{{s}_{i}}\text{cos}{{\varphi }_{ci}}}{T}. \\ & {{\left( \text{d}x \right)}_{i}}={{s}_{i}}\text{cos}{{\varphi }_{ci}}, \\ & {{\left( \text{d}y \right)}_{i}}={{s}_{i}}\text{sin}{{\varphi }_{ci}}.\text{ } \\ \end{align}$ |
定义一系列量纲一的系数:
| $x=\frac{x}{L},s=\frac{{{s}_{0}}}{L},V=\frac{V{{L}^{2}}}{EI},H=\frac{H{{L}^{2}}}{EI},$ |
式中:L为管线长度,I为惯性矩,E为弹性模量.
则管道大挠度控制微分方程转化为量纲一的形式如下:
| $\frac{{{\text{d}}^{2}}\theta }{\text{d}{{\overline{x}}^{2}}}=\delta \left( \overline{V}\text{cos}\theta -\overline{H}\text{sin}\theta \right).$ | (1) |
式中:
| $\delta =1+\frac{1}{{{\lambda }^{2}}}\left( \overline{H}\text{cos}\theta +\overline{V}\text{sin}\theta \right),{{\lambda }^{2}}=\frac{A{{L}^{2}}}{I}.$ |
由微分求积法可得控制微分方程(1)的微分求积格式为[16]
| $\sum\limits_{j=1}^{N}{A_{_{ij}}^{^{(2)}}}\theta \left( {{\overline{x}}_{j}} \right)+\delta \overline{H}\text{sin}\theta \left( {{\overline{x}}_{i}} \right)-\delta \overline{V}\text{cos}\theta \left( {{\overline{x}}_{i}} \right)=0.$ | (2) |
式中:(i=1,2…,N),N为网点总数,Aij(2)为二阶权系数,xj(x1=0,xN=1)是网点的坐标值,θ(xj)是函数在这些离散点的值. 选取不均匀网点:
| ${{\overline{x}}_{i}}=\frac{1-\text{cos}\left[ \left( i-1 \right)\text{ }\!\!\pi\!\!\text{ }/\left( N-1 \right) \right]}{2},\text{ }$ |
内力的表达式为
| $\begin{align} & {{M}_{i}}=-\frac{EI}{L}\sum\limits_{j=1}^{N}{{}}A_{_{ij}}^{^{(1)}}{{\theta }_{j}}, \\ & {{T}_{w}}_{i}={{H}_{i}}\text{sin}{{\theta }_{i}}+{{V}_{i}}\text{cos}{{\theta }_{i}}. \\ \end{align}$ |
其中1≤i≤N.
2.2 逆Broyden法求解非线性方程组通过微分求积法,管线大挠度微分方程的求解变为对式(2)的求解. 令xi=θ(xi),则式(2)化简为
| $f\left( {{x}_{i}} \right)=\sum\limits_{j=1}^{N}{A_{_{ij}}^{^{(2)}}}{{x}_{j}}+\delta \overline{H}\text{sin }{{x}_{i}}-\delta \overline{V}\text{cos }{{x}_{i}}=0.$ | (3) |
从式(3)可以看出,有x1,x2,…xN和H、V总计n+2个参数是未知的,而只有n个方程. 假设水平拉力H和竖直拉力V已知,即对非线性方程组(4)的求解:
| $\left\{ \begin{matrix} {{f}_{1}}{{x}_{1}},{{x}_{2}},\cdots {{x}_{n}}=0, \\ \vdots \\ \text{ }{{f}_{n}}{{x}_{1}},{{x}_{2}},\cdots {{x}_{n}}=0. \\ \end{matrix} \right.$ | (4) |
令F=(f1,f2,…,fn)T,x=(x1,x2,…,xn)T,则式(4)可以写成
| $F\left( x \right)=0.$ | (5) |
令yk=F(xk+1)-F(xk),sk=xk+1-xk. 由逆Broyden法[17]可得非线性方程组(5)算法步骤如下:
Step 1 给定初始近似值x0∈Rn及计算精度要求的ε1与ε2;
Step 2 计算初始矩阵H0∈Rnn,可取H0=[F′(x0)]-1或单位矩阵I;
Step 3 k=0,计算F(x0);
Step 4 计算sk=-HkF(xk),xk+1=xk+sk;
Step 5 计算F(xk+1),如若‖F(xk+1)‖ <ε1或‖sk‖≤ε2,则转Step 8,否则转Step 6;
Step 6 计算yk=F(xk+1)-F(xk);
Step 7 k=k+1,转Step 4;
Step 8 x*=xk+1,结束.
显然,这个过程需要水平拉力H和竖直拉力V已知,即可求解.
2.3 利用边界条件确定水平拉力H和竖直拉力V初始铺管作业过程中,对于管道,如果已知张紧器张力及管道下端所受力水平力H与垂直力V,则可根据管道挠度无量纲方程. 算出管道形态及管道所受弯矩M及轴向力N的. 对于缆索,如果已知一端所受的张力T 和角度φci,则可根据式(2),从缆索已知端开始逐段计算,直至求出整条缆索的形态和内力. 但是,在实际起始铺管作业过程中管道下端的坐标和缆索所受张力都是未知的,即管道下端的边界条件是未知的. 由于管道下端和缆索相连,根据静力平衡可知缆索和管道内的张力大小相等而方向相反,又因为缆索刚度极小基本可以忽略,所以管道下端所受弯矩为0.
已知的变量有张紧器张力T、管道长度L、缆索长度S、起始锚坐标、船体坐标、船舶六自由度及管道物理参数.
首先,定义一系列数组和变量如下:
Ti为管道第i段拉力;Hi为管道第i段水平拉力;Vi为管道第i段竖直拉力;θi为管道第i段转角;Mi为管道第i段弯矩;其中(i=1,2,…,N),第N点为管道与缆索连接点(如图 2点B). 对于初始铺管过程中每一时刻,定义一个数组DH(10):用于存储管道下端水平拉力;数组de(10):用于存储误差;dt为水平拉力平均分成10份,每份大小为dt;e为计算精度.
由管线微段受力(图 1)受力分析可得
| $\begin{align} & {{M}_{i}}={{H}_{i}}d{{y}_{0}}-{{V}_{i}}d{{x}_{0}}-w2d{{x}_{0}}^{2},\text{ } \\ & {{T}_{i}}={{H}_{i}}cos{{\theta }_{i}}+{{V}_{i}}sin{{\theta }_{i}}. \\ \end{align}$ |
由管道下端所受弯矩为0,即由边界条件MN=0可得
| ${{V}_{N}}={{H}_{N}}\text{tan}{{\theta }_{N}}-\frac{w}{2}\left( {{x}_{N}}-{{x}_{N-1}} \right),$ |
进行量纲一化得
| ${{\overline{V}}_{N}}={{\overline{H}}_{N}}\text{tan}{{\theta }_{N}}-\frac{w{{L}^{2}}}{2EI}\left( {{x}_{N}}-{{x}_{N-1}} \right).$ | (6) |
通过式(6)以看出,只要给出HN,就能计算出VN,这样减少了迭代过程中的未知变量,使方程组(4)可以求解. 取起始锚位置为绝对坐标系原点,船体位置坐标(x,y,z)由卫星定位可知.
首先开始第一轮计算. 将管道上端张紧器拉力T平均分成10份,每份的大小为dt=T/10,取DH(i)=idt(i=1,2,…,N),对应每个DH(i),计算出管道横跨距离${{X}_{1}}=\sum\limits_{i=1}^{N}{{{d}_{t}}}{{x}_{i}}$,缆索横跨距离${{X}_{0}}=\sum\limits_{i=1}^{N}{{{d}_{t}}{{x}_{i}}}$,由于X0+X1应等于船体坐标X,所以可以计算出每个DH(i)对应的误差为
| ${{d}_{e}}\left( i \right)={{X}_{0}}+{{X}_{1}}-X.$ |
然后判断出10个de (i)中最小的一个,其下标定为I,从而DH(I)对应的误差de (I)是最小的一个,即DH(I)是最接近精确解的.
第一轮计算完毕,进行下一轮的逼近计算. 在DH(IP)附近取10个点组成新的DH(10). 根据DH(IP)值的特点,分3种情况计算:
1) 如果DH(I)是10个中最小的,则取DH(1)=DH(I),dt=dt/9,DH(i)=DH(1)+(i-1)dt,i=2,…10.
2) 如果DH(I)是10个中最大的,则取DH(1)=DH(I-1),dt=dt/9,DH(i)=DH(1)+(i-1) dt,i=2,…10.
3) 如果DH(I)在10个中不是最大也不是最小的,则取DH(1)=DH(I-1),dt=2dt/9,DH(i)=DH(1)+(i-1) dt,i=2,…10.
这样就定了新一轮计算的水平拉力DH(10). 值得注意的是,为保证每轮计算中都有10个元素,第一轮逼近中总共分割了10份,去掉为0的点,取上面10个点作为输入. 而第二轮计算中由于第一个点不为0,所以分割了9份,取全部10点作为输入.
如此反复进行直到前后两轮计算所得的DH(I)的差值满足精度要求为止,至此求出了管道长度为L时管道下端水平拉力H. 至此就能求解非线性方程组(4),就可以求出管道和缆索形态及内力分布.
3 仿真实例验证及其结果分析 3.1 仿真作业算例为了验证初始铺管作业理论分析的准确性、数值解算方法的快速性及稳定性,铺管作业仿真系统数学模型海况输入采用第3方提供的DP数据. 此次算例水深1 000 m,管道直径323.9 mm,壁厚15.9 mm;缆绳长度为1 000 m,缆绳外径0.108 m,密度7 850 kg/m3;托管架长度和曲率半径分别为87 m和85 m. 为便于分析,提供铺管过程中的6种状态对应的长度及张力(见表 1).
| 表 1 起始铺管管道长度及张力 |
将仿真结果与理论数据对比,验证1 000 m水深海底管道起始铺设过程中管道和缆索的形态、轴力及弯矩分布. 仿真的管线形态如下图 5(a)~(f),节点上部分为管道,下部分为缆索形态.

|
图 5 初始铺管管道和缆索形态 |
图 5中实线代表仿真得到的曲线,虚线为商业软件OFFPIPE计算得到的本次案例曲线,均为静态管道铺设形态. 结果表明,随着铺管作业的进行,管道长度逐渐增加,管道下端高度逐渐降低. 从S1~S3可以看出,管道和缆索形态逐渐变平缓,缆索触底点的位置逐步远离铺管船,而在S3~S6中,缆索触底点重新向铺管船靠近,铺管形态又变得陡峭.
在起始铺管S1~S6中,管道上端的张力从180.0 kN逐渐增加到400.0 kN,铺管作业过程中,起始铺管轴力分布见图 6,起始铺管弯矩分布见图 7.
由图 6、7可以看出,S1~S6过程中,缆索最大轴力逐渐变小,轴力变化趋势逐渐变缓,S1时最陡,S6时最缓;缆索内没有弯矩,这是由于假设缆索的抗弯刚度为零.

|
图 6 起始铺管轴力分布 |

|
图 7 起始铺管弯矩分布 |
1) 对初始铺管作业过程中的管道与缆索进行受力分析. 在原有的铺管常用算法基础上提出了将非线性弹性大挠度梁理论应用于初始铺管计算,建立管道数学模型,采用微分求积法求解,同时建立缆索模型,并用迭代法求解. 微分求积法极大地减少了计算量且求解精度较高,求解过程易于在计算机上程序实现,提高实时仿真的真实度,有助于视景仿真系统的开发.
2) 在求解微分过程中,基于管道与缆索微分方程边界条件难以确定导致方程无法求解的问题,采用一种基于微分求积法的迭代方法,完成边界条件的确立,然后用拟牛顿法完成方程组的求解. 利用已知的边界条件迭代求出所需的边界条件,在一定的误差范围内结束迭代,结果表明,此方法有效解决了边界条件问题.
3) 仿真得到的管道和缆索形态曲线与项目组提供的本次案例曲线的比较表明,仿真求解得到的曲线与理论曲线基本一致,表明作业理论分析的准确性高,数值方法解算速度快,稳定性好.
| [1] |
PLUNKETT R. Static bending stresses in catenaries and drill strings[J].
Journal of Manufacturing Science and Engineering,1967, 89 (1) : 31-36.
( 0) 0)
|
| [2] |
DAREING D W, NEATHERY R F. Marine pipeline analysis based on Newton’s method with an arctic application[J].
Journal of Manufacturing Science and Engineering,1970, 92 (4) : 827-833.
( 0) 0)
|
| [3] |
CROLL J G A. Bending boundary layers in tensioned cables and rods[J].
Applied ocean research,2000, 22 (4) : 241-253.
( 0) 0)
|
| [4] |
DIXON D A, RUTLEDGE D R. Stiffened catenary calculations in pipeline laying problem[J].
Journal of Manufacturing Science and Engineering,1968, 90 (1) : 153-160.
( 0) 0)
|
| [5] |
顾永宁. 海底管线铺管作业状态分析[J].
海洋工程,1988, 6 (2) : 11-23.
( 0) 0)
|
| [6] |
KALLIONTZIS C. Non-linear finite element simulations of highly curved submarine pipelines[J].
Communications in numerical methods in engineering,1998, 14 (11) : 1067-1088.
( 0) 0)
|
| [7] |
KHDEIR A A. Thermal buckling of cross-ply laminated composite beams[J].
Acta Mechanica,2001, 149 (1/2/3/4) : 201-213.
( 0) 0)
|
| [8] |
DABROWSKI R. Curved thin-walled girders: Theory and Analysis[R]. Workingham: Transport and Road Research Laboratory, 1900.
( 0) 0)
|
| [9] |
花雷.曲梁结构非线性大变形分析[D].扬州:扬州大学,2011.
( 0) 0)
|
| [10] |
李世荣, 孙云, 刘平. 关于Euler-Bernoulli梁几何非线性方程的讨论[J].
力学与实践,2013, 35 (2) : 77-80.
( 0) 0)
|
| [11] |
Jr DENNIS J E, MORÉ J J. Quasi-Newton methods: motivation and theory[J].
SIAM review,1977, 19 (1) : 46-89.
( 0) 0)
|
| [12] |
ZIANI M, GUYOMARC’H F. An autoadaptative limited memory Broyden’s method to solve systems of nonlinear equations[J].
Applied Mathematics and Computation,2008, 205 (1) : 202-211.
( 0) 0)
|
| [13] |
王鑫伟. 微分求积法在结构力学中的应用[J].
力学进展,1995, 25 (2) : 232-240.
( 0) 0)
|
| [14] |
BURDEA G, COIFFET P. Virtual reality technology[J].
Presence: Teleoperators and virtual environments,2003, 12 (6) : 663-664.
( 0) 0)
|
| [15] |
黄玉盈, 朱达善. 海洋管线铺设时的静力分析[J].
海洋工程,1986, 4 (1) : 32-46.
( 0) 0)
|
| [16] |
聂国隽, 仲政. 微分求积单元法在结构工程中的应用[J].
力学季刊,2005, 26 (3) : 423-427.
( 0) 0)
|
| [17] |
马成业, 黄世华. 解非线性方程组的一个改进牛顿法[J].
甘肃联合大学学报(自然科学版),2009, 23 (1) : 116-117.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


