2. 哈尔滨工业大学深圳研究生院 机电工程与自动化学院, 广东 深圳 518055
2. School of Mechanical Engineering and Automation, Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, Guangdong, China
近些年,义齿的制作向个性化、美观、高效等要求发展[1]. 传统的烤瓷牙多采用手工制作,工艺繁琐,制作效率低,病人就诊次数多,返工率高. 而牙科CAD/CAM数控加工技术的应用避免了义齿繁琐的制作过程,可一次加工成型,病人一次就诊即可[2]. 面向义齿加工的CAM技术在口腔修复领域得到了迅速发展,新材料结合CAM加工技术在中国日益得到关注[3-4]. 氧化锆陶瓷因具有可以代替钛等合金材料的卓越理化材料性能,优异的生物相容性,同时接近天然牙齿的自然色泽[5-7],在口腔修复领域的应用日益广泛[8-9]. 在CAM加工中,由于完全烧结的氧化锆陶瓷材料的硬度高,直接加工效率低. 二次烧结技术是指利用初次烧结的氧化锆(硬度较低)进行加工,然后进行二次烧结得到义齿. 研究表明[10-11],和一次烧结相比,二次烧结的氧化锆陶瓷性能相差不大,但可加工性大大提升. Kato等[12]发现用850 ℃初次烧结氧化锆的加工质量最好. 雷小宝等[13-14]研究了初次烧结氧化锆陶瓷的磨削和铣削加工,并在铣削中通过实验建立粗糙度与工艺参数的函数关系,以粗糙度最小为目标优化工艺参数,并用JDPaint软件进行了刀路规划. 在对义齿的加工规划中,吕培军等[15]采用Surfacer 10.5进行义齿的规划加工. 韩景芸等[16]应用两面对称加工方法和最大相贯线法给出了后牙金属全冠的CAM工艺技术流程. 段军军等[17]采用Powermill软件进行了义齿加工的刀路规划. 目前,对初次氧化锆陶瓷的齿科修复体加工中,其各加工阶段参数的优化选择、加工效率研究还不够深入. UG作为国内外通用的CAD/CAM系统软件,具有强大的曲面粗精加工功能,但在义齿修复体制造的加工路径规划方面应用鲜有报道.
本文研究初次烧结氧化锆陶瓷义齿铣削加工时工艺参数合理选择和刀具路径规划方式问题,以提高材料去除率和降低表面粗糙度为指标,采用不同方法优化精加工阶段的工艺参数;以磨牙冠表面加工为例,选用优化得到的工艺参数,采用UG CAM系统规划粗、精加工阶段的刀具路径,通过加工实验验证不同精加工刀具路径规划方式对表面质量的影响,以探索合适的刀具路径规划方法.
1 铣削工艺参数的选择切削参数影响加工效率和质量,对其进行优化是加工过程的重要环节,尤其对于数控加工[18-20]. 和一般的工件加工相比,磨牙冠的加工更为复杂,精度要求更高. 考虑到磨牙冠尺寸较小,本文中把加工工序分为粗加工和精加工两类,对两个过程工艺参数分别进行优化,以加工出好的牙冠表面.
1.1 粗加工阶段粗加工以提高加工效率为目标. 在铣削加工中,单位时间工件材料去除率是衡量铣削加工效率的一个重要指标,去除率Q越大,加工效率越高,且
| $Q = {a_e}{a_p}{f_z}nN.$ | (1) |
式中:ae为切削宽度(mm),ap为切削深度(mm),fz为每齿进给量,n为转速(r/min),N为刀具齿数.
初次烧结氧化锆陶瓷在进行粗加工时易出现边缘碎裂现象,破坏毛坯,需对转速、切削深度和每齿进给量加以限制[14]. 最终选取:转速n=21 000 r/min,切削深度ap=0.2 mm,每齿进给量fz=0.024 mm,铣削方式选择顺铣. 由式(1)可以看出,选定n、fz和ap后,要提高加工效率,需较大的刀具齿数N和切削宽度ae,考虑到尺寸形貌特征不规范以及后续精加工的高效性,刀具的直径不宜过大,选择Φ2 mm四刃平头铣刀,ae=0.4 mm,此时材料去除率为Q=161.28 mm3/min.
1.2 精加工阶段精加工以保证加工表面高质量为目标. 在一般的铣削加工中,对本阶段的处理通常是将表面质量(常用表面粗糙度表示)的值限制在一定的范围内,而不是处于极端状态(如最大值或最小值); 因此一般选择表面粗糙度为约束,以加工效率为目标函数. 在初次烧结氧化锆陶瓷义齿的精加工铣削中,要求加工好的牙冠表面质量好,粗糙度<10 μm,在希望磨牙牙冠加工表面质量更好的同时,因为后续再次进行热处理也需要时间,所以在精加工阶段不但要考虑表面粗糙度,也要结合加工效率,以确定最优工艺参数值.
1.2.1 优化模型建立以最大材料去除率和最小粗糙度为目标函数,以各个参数的稳定区域为约束条件. 精加工刀具切深、切宽小于粗加工,主轴的转速选取n=24 000 r/min. 为更好加工牙冠表面,刀具选择Φ1 mm两刃球头铣刀,铣削方式同样选择顺铣.本文采用参考文献[14]中的表面粗糙度预测模型:
| $\eqalign{ & Ra = 4338.453f_z^2 + 149.3112a_e^2 + 67.7487a_p^2 + \cr & 78.7017{f_z}{a_p} - 13.2805{a_e}{a_p} + 4.6237 - \cr & 152.307{f_z} - 21.9482{a_e} - 14.7756{a_p} - \cr & 35.2801{f_z}{a_e}. \cr} $ | (2) |
联合式(1)、(2),建立两目标优化模型:
| $\left\{ \begin{matrix} \min & Ra, \\ \max & Q. \\ \end{matrix} \right.$ | (3) |
设计变量定义为
| $x={{\left[ \begin{matrix} {{x}_{1}} & {{x}_{2}} & {{x}_{3}} \\ \end{matrix} \right]}^{T}}={{\left[ \begin{matrix} {{f}_{z}} & {{a}_{p}} & {{a}_{e}} \\ \end{matrix} \right]}^{T}}.$ |
因为始终有Q>0,故将目标优化模型(3)转变为
| $\left\{ \begin{align} & \min {{f}_{1}}\left( x \right)=4.6237+4338.453x_{1}^{2}+67.7487x_{2}^{2}+ \\ &\qquad 149.3112x_{3}^{2}+78.7017{{x}_{1}}{{x}_{2}}- \\ &\qquad 35.2801{{x}_{1}}{{x}_{3}}-13.2805{{x}_{2}}{{x}_{3}}- \\ &\qquad 152.307{{x}_{1}}-14.7756{{x}_{2}}-21.9482{{x}_{3}}, \\ & \min {{f}_{2}}\left( x \right)={{Q}^{-1}}={{\left( nN{{f}_{z}}{{a}_{p}}{{a}_{e}} \right)}^{-1}}={{\left( 48000{{x}_{1}}{{x}_{2}}{{x}_{3}} \right)}^{-1}}. \\ \end{align} \right.$ | (4) |
将变量用x替换,模型的约束[21]为
| $\left\{ \matrix{ 0.018 \le {x_1} \le 0.023, \hfill \cr 0.12 \le {x_2} \le 0.15, \hfill \cr 0.04 \le {x_3} \le 0.06; \hfill \cr} \right.或\left\{ \matrix{ 0.018 \le {x_1} \le 0.023, \hfill \cr 0.12 \le {x_2} \le 0.15, \hfill \cr 0.11 \le {x_3} \le 0.12 \hfill \cr} \right.$ | (5) |
由式(4)、(5)可最终得多目标优化数学模型:
| $\eqalign{ & \min {f_i}\left( x \right)\left( {i = 1,2,} \right),x = {\left[ {\matrix{ {{x_1}} & {{x_2}} & {{x_3}} \cr } } \right]^T}, \cr & s.t.{\left[ {\matrix{ {0.018} & {0.12} & {0.04} \cr } } \right]^T} \le x \le {\left[ {\matrix{ {0.023} & {0.15} & {0.06} \cr } } \right]^T}; \cr & A{\left[ {\matrix{ {0.018} & {0.12} & {0.11} \cr } } \right]^T} \le x \le {\left[ {\matrix{ {0.023} & {0.15} & {0.12} \cr } } \right]^T}. \cr} $ | (6) |
为获得较好的优化结果,采用化多为少法,将两目标优化转化为单目标优化问题,采用以下3种方法:
1) 用理想点法求出分目标函数在约束的最优解,使各分目标向理想值逼近,距离最近处所对应的各参数值可作为最优解. 选分函数最小值为理想值,将两目标函数变为单目标函数,可得
| $F\left( x \right) = {\left( {\frac{{{f_1}\left( x \right) - f_{1\min }^*}}{{f_1^*}}} \right)^2} + {\left( {\frac{{{f_2}\left( x \right) - f_{2\min }^*}}{{f_2^*}}} \right)^2}.$ |
式中,f*1min、 f*2min为两个分目标函数在约束内的最小值,计算结果如表 1所示.
| 表 1 f1(x)、 f2(x)在参数区间中的最大值、最小值及对应的参数值 |
2) 最小偏差法
| $F\left( x \right) = \frac{{{f_1}\left( x \right) - f_{1\min }^*}}{{{f_{1\max }} - f_{1\min }^*}} + \frac{{{f_2}\left( x \right) - f_{2\min }^*}}{{{f_{2\max }} - f_{2\min }^*}}.$ |
式中:f1max、f2max为两个分目标函数在约束内的最大值,计算结果如表 1所示.
3) 线性组合法优化,可通过线性组合方法体现对各分目标函数的重视程度. 因各目标函数在量纲与量级上的不同,对结果产生影响,用线性转化法对函数进行处理,以消除影响,转化公式如下:
| $\left\{ \begin{align} & f_{1}^{'}\left( x \right)=\left( {{f}_{1}}\left( x \right)-f_{1\min }^{*} \right)/f_{1\min }^{*}, \\ & f_{2}^{'}\left( x \right)=\left( {{f}_{2}}\left( x \right)-f_{2\min }^{*} \right)/f_{2\min }^{*}. \\ \end{align} \right.$ |
对处理后的分目标函数进行线性组合,将多目标函数转化为单目标函数:
| $F\left( x \right)={{w}_{1}}f_{1}^{'}\left( x \right)+{{w}_{2}}f_{2}^{'}\left( x \right).$ |
式中,w1,w2为权系数,其取值大小表示对相应函数的重视程度,且有w1+w2=1. 权系数的大小,反映了对各分目标的不同折衷估价. 考虑到磨牙冠加工精度要求较高,粗糙度分目标函数的权重可大一些,令w1=0.8,w2=0.2,则
| $F\left( x \right)=0.8f_{1}^{'}\left( x \right)+0.2f_{2}^{'}\left( x \right).$ |
采用MATLAB优化工具箱,优化结果见如表 2.
| 表 2 3种方法的优化结果 |
由表 2可知,方法1可以获得最大的加工效率,可是粗糙度值最大,即加工质量最差;方法2则相反,其可以获得最好的表面质量,但是加工效率最低,加工用时长;方法3的结果介于两者之间,虽然其粗糙度值比采用最小偏差法的大,可是增加幅度不大,但其加工效率提高要明显得多. 综合考虑加工用时以及质量,选用线性组合方法的结果,即取相应的变量值为 x1=0.020 1,x2=0.139 2,x3=0.11,圆整后得x0=[0.02,0.14,0.11]Τ.
综合以上分析,各加工阶段的工艺参数最终取值如表 3所示.
| 表 3 铣削过程工艺参数的选择结果 |
本文使用UG CAM进行刀具路径规划,生成加工代码. 考虑到磨牙冠的曲面特征复杂以及片体机构特征,粗加工采用UG CAM的型腔铣削方式,精加工采用固定轴曲面轮廓铣削方式. 采用UG进行数控加工一般分为3步:第1步,调整加工环境,包括导入模型、毛坯选择以及坐标系调整等;第2步,生成加工路径,包括建立加工用刀具,选择加工方法以及计算生成刀具轨迹;第3步,生成加工代码,包括验证是否碰撞等,将刀具轨迹转化为特定数控机床能识别的NC代码等.
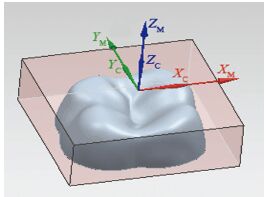
磨牙冠模型如图 1所示,导入UG加工模块中,可通过方形块、圆形或者圆柱体等方式来定义毛坯. 根据磨牙冠模型的结构特点,选择方形毛坯,如图 2所示,加工坐标系经调整位于方形毛坯上表面中心点处.
|
图 1 磨牙冠表面模型 |
|
图 2 毛坯形状及加工坐标系示意 |
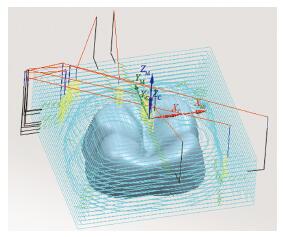
针对磨牙冠表面模型的特殊形貌,粗加工阶段选择型腔铣,在其切削模式中选择跟随周边模式,加工余量0.25 mm左右,生成的加工刀具轨迹见图 3.
|
图 3 粗加工阶段的刀具加工路径示意 |
磨牙冠表面属于尺寸微小的复杂曲面,难以直接通过数学特征建立模型,往往通过扫描方式基于逆向重构技术得到模型. 模型以STL格式呈现,即原实体模型表面用很多空间小三角形表面逼近[22],没有具体的曲面曲线特征,故在UG固定轴铣的加工中部分策略不可用. 目前,UG8.0版本中可选的驱动方法主要有区域铣削驱动方法和曲面驱动方法 两种. 另外,在区域铣削中,较合适的切削模式也有两种:往复模式和跟随周边模式.
数控加工中,加工方式对于加工效率和加工质量有着重要的影响,有效的刀具轨迹直接决定了数控加工的可能性、质量与效率[23]. 为了得到更好的加工效果,比较曲面往复铣削方法、区域往复铣削方法以及区域铣削方法跟随周边这3种不同的精加工规划方法对最终的加工表面质量的影响. 保持铣削工艺参数和刀具规格均不变,粗加工阶段的刀路规划方式不变,分别用上述3种方式进行精加工刀路规划,结果见表 4. 生成精加工阶段的加工刀具路径见图 4.
| 表 4 基于UG的加工阶段刀具加工路径规划方法 |

|
图 4 不同规划方法的精加工阶段的刀具加工路径示意图 |
规划完成粗加工和精加工阶段的刀具路径后,可利用UG自带的仿真功能,经模拟加工和检验确定无误后,根据选用的机床及数控系统后处理导出NC程序. UG提供了丰富的后处理器,因实验室目前只用三轴的数控机床,且磨牙冠上表面可通过三轴加工即可实现,故直接导出了相应的NC程序进行加工.
3 加工实验 3.1 实验设备三轴数控铣床LGMazak_VTC160AN,装载马扎克系统(Mazatrol Fusion 640);Φ2 mm四刃平头铣刀,型号S5502.0×4×6×50,三把;Φ1 mm两刃球头铣刀,型号GM-2B-R0.5,3把;初次烧结氧化锆陶瓷(860 ℃烧结),12 mm×12 mm×12 mm,3块.
3.2 实验结果将3种加工规划方法生成的NC程序导入机床,进行铣削加工. 为排除刀具磨损对表面质量的影响,每次使用新的铣刀以及陶瓷块. 3个规划方法下加工得到的磨牙冠表面如图 5所示. 对比牙冠(a)和牙冠(c)可发现,采用曲面驱动方法往复模式规划产生的精加工NC代码,加工得到的牙冠上留有明显地刀路痕迹,加工表面质量较差; 对于区域铣削驱动方法,对比牙冠(b)和牙冠(c)发现,采用跟随周边模式时,牙冠上一些凹处的加工不理想,遗留有刀路痕迹,加工质量要差一些;而采用区域铣削往复模式,牙冠表面质最好. 综上,在当前铣削工艺参数和铣刀规格条件下,采用区域铣削驱动方法中规划精加工刀路要比曲面铣削好,且在区域铣削中,采用往复模式比跟随周边模式得到的模型表面质量好

|
图 5 不同规划方式加工后的磨牙冠上表面模型 |
1)以初次烧结氧化锆陶瓷为加工材料,进行了粗、精加工阶段的工艺参数选择. 在粗加工阶段,基于加工效率,参数取值为主轴转速21 000 r/min、每齿进给量0.024 mm、切削深度0.20 mm、切削宽度0.40 mm;在精加工阶段,通过对理想点法、最小偏差法和线性组合法优化结果的比较分析,发现线性组合法优化效果较好,参数取值为主轴转速24 000 r/min、每齿进给量0.020 mm、切削深度0.14 mm、切削宽度0.11 mm;
2)比较了采用固定轴铣的精加工阶段3种不同的刀具路径规划方式(曲面铣削往复模式、区域铣削跟随周边模式及区域铣削往复模式)对加工表面的影响,在当前铣削工艺参数和加工环境下,采用区域铣削驱动中的往复切削模式规划精加工刀路,加工得到的表面质量最好;
3)实际加工中,利用UG规划路径,粗加工选择型腔铣跟随周边模式,精加工选择区域铣削往复切削模式规划刀路,加工后的义齿表面质量最好.
| [1] |
田芝娟, 苏俭生. CAD/CAM口腔修复技术的研究现状[J].
中华老年口腔医学杂志,2008 (3) : 179-182.
( 0) 0)
|
| [2] |
李晓萌, 高平. 牙科CAD/CAM系统的主要技术构成及研究现状[J].
口腔颌面修复学杂志,2005, 6 (4) : 299-301.
( 0) 0)
|
| [3] |
于海洋. 关于我国口腔修复工艺学的思考[J].
中华口腔医学研究杂志(电子版),2008 (1) : 83-85.
( 0) 0)
|
| [4] |
柳红芹, 朱国威. CAD/CAM氧化锆全瓷冠在口腔修复领域中的应用研究[J].
遵义医学院学报,2011 (2) : 190-193.
( 0) 0)
|
| [5] |
PICONI C, MACCAURO G. Zirconia as a ceramic biomaterial[J].
Biomaterials,1999, 20 (1) : 1-25.
( 0) 0)
|
| [6] |
TINSCHERT J, NATT G, MAUTSCH W, et al. Fracture resistance of lithium disilicate-, alumina-, and zirconia-based three-unit fixed partial dentures: a laboratory study[J].
International Journal of Prosthodontics,2001, 14 (3) : 231-238.
( 0) 0)
|
| [7] |
MANICONE P F, IOMMETTI P R, RAFFAELLI L. An overview of zirconia ceramics: basic properties and clinical applications[J].
Journal of Dentistry,2007, 35 (11) : 819-826.
( 0) 0)
|
| [8] |
孙凤, 张桂荣, 张峰, 等. CAD/CAM氧化锆全瓷在口腔修复领域的应用[J].
上海口腔医学,2006, 15 (4) : 337-344.
( 0) 0)
|
| [9] |
李伟, 蒋丽, 廖运茂. 牙科氧化锆全瓷材料[J].
中国实用口腔科杂志,2010, 3 (8) : 455-457.
( 0) 0)
|
| [10] |
孙蕾, 张富强, 高益鸣, 等. 二步烧结牙科氧化锆陶瓷细胞毒性评价[J].
口腔颌面修复学杂志,2008 (1) : 1-4.
( 0) 0)
|
| [11] |
黄慧, 魏斌, 张富强, 等. 两次烧结工艺对氧化锆陶瓷性能的影响[J].
华西口腔医学杂志,2008 (2) : 175-178.
( 0) 0)
|
| [12] |
KATO K, SHYU C S. Machining of semi-sintered zirconia and its full-sintering for final shape[J].
VDI Berichte,1996 (1276) : 427-434.
( 0) 0)
|
| [13] |
雷小宝, 廖文和, 张霖, 等. 部分烧结氧化锆陶瓷的齿科修复体磨削加工[J].
重庆大学学报,2011 (8) : 80-85.
( 0) 0)
|
| [14] |
雷小宝. 预烧结氧化锆义齿高速铣削加工关键技术与装备研究[D]. 南京: 南京航空航天大学, 2012: 53-57, 77-79.
( 0) 0)
|
| [15] |
吕培军, 王勇, 邹波, 等. 国产口腔修复CAD-CAM系统的研究与开发[J].
中华口腔医学杂志,2002 (5) : 47-50.
( 0) 0)
|
| [16] |
韩景芸, 费仁元, 李彦生, 等. 金属全冠的CAM工艺技术研究[J].
现代制造工程,2004 (10) : 10-12.
( 0) 0)
|
| [17] |
段军军, 罗学科. 基于powermill的stl义齿模型数控编程的研究[J].
装备制造技术,2009 (4) : 3-5.
( 0) 0)
|
| [18] |
SARAVANAN R, ASOKAN P, SACHITHANANDAM M. Comparative analysis of conventional and non-conventional optimization techniques for CNC turning process[J].
The International Journal of Advanced Manufacturing Technology,2001, 17 (7) : 471-476.
( 0) 0)
|
| [19] |
LI J G, ZHAO H, YAO Y X, et al. Off-line optimization on NC machining based on virtual machining[J].
The International Journal of Advanced Manufacturing Technology,2008, 36 (9/10) : 908-917.
( 0) 0)
|
| [20] |
李建广, 赵航, 盛敏. 基于虚拟加工的数控车削过程优化[J].
哈尔滨工业大学学报,2010 (11) : 1740-1743.
( 0) 0)
|
| [21] |
LIU Junwei, YANG Xiaojun. Effect of milling parameters on surface roughness for high-speed milling of pre-sintering zirconia[J].
Advanced Materials Research,2014, 998 : 253-256.
( 0) 0)
|
| [22] |
王跃平, 薛祥. STL实体的有限差分网格高效剖分算法[J].
哈尔滨工业大学学报,2012, 44 (5) : 101-105.
( 0) 0)
|
| [23] |
乐英, 韩庆瑶, 贾军. 复杂曲面数控加工刀具轨迹的生成技术[J].
机床与液压,2008, 36 (6) : 25-27.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


