混联机床是在串联机床和并联机床的基础上发展而来的,该机床结合了串联机床工作空间大,并联机床高刚度[1-2]、高精度[3-4]等优点,能够实现对自由曲面零件的加工[5]. 混联机床与传统的数控机床不同,由于混联机床中的并联机构各驱动杆运动坐标轴与工件笛卡尔坐标轴之间存在非线性关系,现有的数控系统无法直接对混联机床进行控制,因此,需要根据混联机床的控制需求开发相应的控制系统,而后置处理是机床控制系统的核心,其正确性关系到机床的精度和加工效率[6-7]. 后置处理是指由工件刀位数据生成机床数控代码的过程,包括刀位点插补、坐标变换、逆解以及干涉检查等[8-10]. 文献[11-12]分别在UG/Post和IMS/Post软件的基础上开发了面向混联机床的专用后置处理模块,这种开发方法不但要求开发人员熟练掌握宏语言,而且限制了混联机床数控系统的开放性;文献[13-15]分别采用DOS、Linux和Visual Basic等高级语言开发面向CAM刀位数据的后置处理器,该方法要求开发人员在了解混联机床的基础上,掌握对刀位数据的识别和处理过程,这种方法的开放性好,但是对不同CAM生成的刀位数据识别和处理过程繁琐.
本文在C++语言基础上,提出解决XYZ-3RPS混联机床后置处理问题的可行性方法,同时指出刀位数据的识别、插补、坐标变换、逆解以及机床干涉检查是后置处理的关键问题,并给出了解决相应问题的简便算法. 通过多次加工实例验证了算法的实用性和有效性.
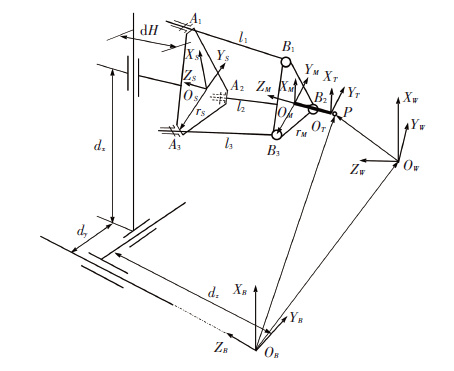
1 混联机床结构模型6轴卧式混联机床结构模型是采用在串联机构X轴的末端执行器位置安装3RPS并联机构的方法建立的,如图 1所示. 该机床通过串联机构来增大机床的工作空间,利用3RPS并联机构改变刀具的姿态. 并联机构由3根驱动杆AiBi(i=1,2,3)、动平台B1B2B3和定平台A1A2A3组成,驱动杆两端通过转动副Ai(i=1,2,3)和球铰Bi(i=1,2,3)分别与定平台和动平台相连. 串联机构和并联机构都采用丝杠螺母副实现杆长的伸缩变化. 需要建立5个坐标系描述混联机床:机床坐标系OBXBYBZB;工件坐标系OWXWYWZW;动平台坐标系OMXMYMZM;定平台坐标系OSXSYSZS;刀具坐标系OTXTYTZT. 下文分别使用{B}、{W}、{M}、{S}、{T}表示机床坐标系、工件坐标系、动平台坐标系、定平台坐标系、刀具坐标系. 其中动平台坐标系{M}坐标原点在球铰所在圆的圆心处,球铰呈120°均匀分布. 定平台坐标系{S}坐标原点在定平台转动副所在圆的圆心处,转动副呈120°均匀分布.
|
图 1 6 轴卧式混联机床结构模型 |
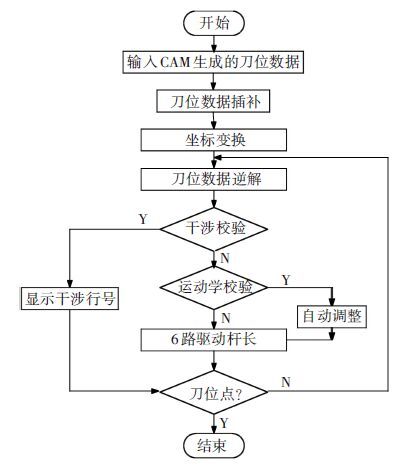
面向6轴卧式混联机床后置处理过程:将CAM软件生成的刀位信息,包括刀头点在工件坐标系{W}的位置信息(xTW,yTW,zTW)和刀具在工件坐标系下的姿态信息(iTW,jTW,kTW)转换为机床的6路驱动杆长(dx,dy,dz,l1,l2,l3). 在后置处理过程中要经过插补模块、坐标转换模块、逆解模块、干涉校验模块、速度校验模块等,最后输出驱动文件行号、6路驱动杆长、进给速度等信息. 后置处理过程如图 2所示.
|
图 2 混联机床后置处理流程 |
现有的CAM软件不能直接生成面向混联机床的驱动文件,开发相应的后置处理系统是十分必要的. 该系统具备的基本功能为:识别不同CAM软件生成的刀位数据、刀位数据插补、坐标变换、刀位数据逆解、干涉检查及速度校验.
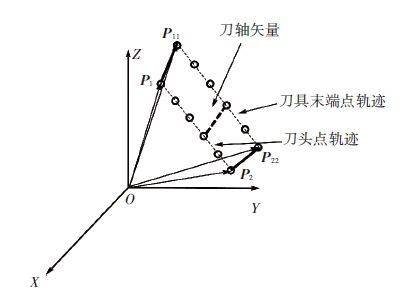
3 刀位数据插补在混联机床中由于并联机构的存在,使刀具位姿与驱动杆长之间是非线性对应关系,当各个驱动杆长发生变化时刀具轨迹变化是非线性的. 为了降低两者之间的偏差,将刀位数据密集化是十分必要的. 不同CAM软件对刀具位姿表示方法不同,本文采用(xTW,yTW,zTW,iTW,jTW,kTW)描述刀位信息,然后对刀具位姿的6个坐标参数分别直线插补,保证刀具的位置和姿态的连续性,如图 3所示.
|
图 3 插补算法 |
在工件坐标系{W}下,已知刀具起点位置和姿态分别为p1=[x1,y1,z1]T、w1=[i1,j1,k1]T,刀具终点位置和姿态分别为p2=[x2,y2,z2]T、w2=[i2,j2,k2]T. 确定刀具末端点的起点和终点分别为
| ${{p}_{11}}=\left[ \begin{matrix} {{x}_{1}} \\ {{y}_{1}} \\ {{z}_{1}} \\ \end{matrix} \right]+h\cdot \left[ \begin{matrix} {{i}_{1}} \\ {{j}_{1}} \\ {{k}_{{}}} \\ \end{matrix} \right],{{p}_{22}}=\left[ \begin{matrix} {{x}_{2}} \\ {{y}_{2}} \\ {{z}_{2}} \\ \end{matrix} \right]+h\cdot \left[ \begin{matrix} {{i}_{2}} \\ {{j}_{2}} \\ {{k}_{2}} \\ \end{matrix} \right].$ |
式中h为刀具长度.
首先,确定插补步数:
| $N=\max \left( \frac{\left| {{p}_{2}}-{{p}_{1}} \right|}{\Delta d}+1,\frac{\left| {{p}_{22}}-{{p}_{11}} \right|}{\Delta d}+1 \right),$ |
式中Δd为插补步长.
然后,对刀头点轨迹和刀具末端轨迹分别插补:
| $\begin{align} & \left[ \begin{matrix} {{x}_{1n}} \\ {{y}_{1n}} \\ {{z}_{1n}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{x}_{1}} \\ {{y}_{1}} \\ {{z}_{1}} \\ \end{matrix} \right]+\frac{n}{N-1}\left[ \begin{matrix} {{x}_{2}}-{{x}_{1}} \\ {{y}_{2}}-{{y}_{1}} \\ {{z}_{2}}-{{z}_{1}} \\ \end{matrix} \right], \\ & \left[ \begin{matrix} {{x}_{11n}} \\ {{y}_{11n}} \\ {{z}_{11n}} \\ \end{matrix} \right]=\left[ \begin{matrix} {{x}_{11}} \\ {{y}_{11}} \\ {{z}_{11}} \\ \end{matrix} \right]+\frac{n}{N-1}\left[ \begin{matrix} {{x}_{22}}-{{x}_{11}} \\ {{y}_{22}}-{{y}_{11}} \\ {{z}_{22}}-{{z}_{11}} \\ \end{matrix} \right]. \\ \end{align}$ |
式中:n=1,2,…,N-1.
最后,对刀位数据进行姿态插补:
| $\left[ \begin{matrix} {{i}_{n}} \\ {{j}_{n}} \\ {{k}_{n}} \\ \end{matrix} \right]=\frac{1}{\Delta h}\cdot \left[ \begin{matrix} {{x}_{11n}}-{{x}_{1n}} \\ {{y}_{11n}}-{{y}_{1n}} \\ {{z}_{11n}}-{{z}_{1n}} \\ \end{matrix} \right].$ |
式中:
| $\begin{matrix} \Delta h=\sqrt{{{({{x}_{11n}}-{{x}_{1n}})}^{2}}+{{({{y}_{11n}}-{{y}_{1n}})}^{2}}+{{({{z}_{11n}}-{{z}_{1n}})}^{2}}}; \\ n=1,2,\cdots N-1. \\ \end{matrix}$ |
通过该算法能够实现对CAM生成的刀位数据两点之间插入若干个点(x1n,y1n,z1n,in,jn,kn),并生成新的刀位数据.
4 刀位数据逆解混联机构的姿态变化通常使用RPY变换的方法描述,但是这种方法描述混联机构的姿态不够直观,本文采用Euler角变换的方法描述刀具位姿. 例如采用Euler变换将动平台坐标系{M}相对于定平台坐标系{S}进行三次坐标变换:首先绕动平台坐标系{M}的ZM轴转动α角(进动角);其次绕动平台坐标系{M}的YM轴旋转β角(章动角);最后绕动平台坐标系{M}的ZM轴旋转γ角(自旋角). 并且运动坐标系和固定坐标系在初始状态下可以不重合,但坐标轴方向相同,转换矩阵为
| ${}_{M}^{S}T=\left[ \begin{matrix} c\alpha c\beta c\gamma -s\alpha s\gamma & -c\alpha c\beta s\gamma -s\alpha c\gamma & c\alpha s\beta \\ s\alpha c\beta c\gamma +c\alpha s\gamma & -s\alpha c\beta s\gamma +c\alpha c\gamma & s\alpha s\beta \\ -s\beta c\gamma & s\beta s\gamma & c\beta \\ \end{matrix} \right].$ |
式中:MST为Euler角旋转矩阵;s α=sin α,c α=cos α,同理记sβ、cβ、sγ、cγ.
数控加工程序是在工件坐标系下编写的,而数控加工过程却是在机床坐标系下完成的,并且在混联机床中工件坐标系的位置和姿态都是任意的. 因此在建立机床逆解前要识别工件坐标系在机床坐标系下的位置和姿态,再将工件坐标系下的刀位信息转换到机床坐标系下,位姿转换公式为
| $\left[ \begin{matrix} x_{T}^{B} & i_{T}^{B} \\ y_{T}^{B} & j_{T}^{B} \\ z_{T}^{B} & k_{T}^{B} \\ 1 & 0 \\ \end{matrix} \right]=\left[ \begin{matrix} {}_{W}^{B}T & P_{{{O}_{W}}}^{B} \\ 0 & 1 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} x_{T}^{W} & i_{T}^{W} \\ y_{T}^{W} & j_{T}^{W} \\ z_{T}^{W} & k_{T}^{W} \\ 1 & 0 \\ \end{matrix} \right].$ |
式中:[xBTyBTzBT]T为刀头点在机床坐标系下的位置;[iBTjBTkBT]T为刀具在机床坐标系下的姿态;WBT为工件坐标系到机床坐标系的转换矩阵;POWB为工件坐标系原点在机床坐标系的位置.
3RPS并联机构是少自由度的空间机构,描述并联机构姿态6个参数之间存在耦合. 由图 1可知,动平台上球铰中心在动平台坐标系{M}中的坐标:
| $\begin{align} & B_{1}^{M}={{\left[ \begin{matrix} {{r}_{M}} & 0 & 0 \\ \end{matrix} \right]}^{T}}, \\ & B_{2}^{M}={{\left[ -\begin{matrix} {{r}_{M}}/2 & \sqrt{3}\cdot {{r}_{M}}/2 & 0 \\ \end{matrix} \right]}^{T}}, \\ & B_{3}^{M}={{\left[ -\begin{matrix} {{r}_{M}}/2 & -\sqrt{3}\cdot {{r}_{M}}/2 & 0 \\ \end{matrix} \right]}^{T}}. \\ \end{align}$ |
其中rM为动平台半径.
动平台坐标系的坐标原点OM在定平台坐标系{S}下的位置坐标为:POMS=[xOMSyOMSzOMS]T,根据欧拉角变换的旋转矩阵可得动平台铰点在定平台坐标系下的位置:
| $\left[ \begin{matrix} B_{q}^{S} \\ 1 \\ \end{matrix} \right]=\left[ \begin{matrix} {}_{M}^{S}T & P_{{{O}_{M}}}^{S} \\ 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} B_{q}^{M} \\ 1 \\ \end{matrix} \right].$ |
式中:BqS为刀头点在定平台坐标系下的位置,q=1,2,3.
3RPS并联机构的几何约束:在定平台坐标系下3条杆分别在yS=0,yS=-$\sqrt{3}$xS和yS=$\sqrt{3}$xS平面内运动,则α=-γ. 联立方程可得
| $\begin{align} & x_{{{O}_{M}}}^{S}={{r}_{M}}(\cos 2\alpha )(cos\beta -1)/2; \\ & y_{{{O}_{M}}}^{S}={{r}_{M}}(sin2\alpha )(1-\cos \beta )/2. \\ \end{align}$ |
通过分析可知,描述3RPS并联机构位姿的6个参数中独立参数为zOMS、α、β. 转动副中心在定平台坐标系下的位置坐标
| $\begin{align} & A_{1}^{S}={{\left[ \begin{matrix} {{r}_{s}} & 0 & 0 \\ \end{matrix} \right]}^{T}}, \\ & A_{2}^{S}={{\left[ \begin{matrix} -{{r}_{s}}/2 & \sqrt{3}\cdot {{r}_{s}}/2 & 0 \\ \end{matrix} \right]}^{T}}, \\ & A_{3}^{S}={{\left[ \begin{matrix} -{{r}_{s}}/2 & -\sqrt{3}\cdot {{r}_{s}}/2 & 0 \\ \end{matrix} \right]}^{T}}, \\ \end{align}$ |
其中rS为定平台半径,则并联机构的杆长
| ${{l}_{q}}=\left| B_{q}^{s}-A_{q}^{s} \right|.$ |
式中q=1,2,3.
由混联机床的结构特点,建立机床坐标系和定平台坐标系时方向是一致的,刀具安装在动平台上且与动平台的姿态变化是一致的. 转化后的刀位数据中刀具姿态信息用(iBT,jBT,kBT)描述,则可得动平台在运动过程中的Euler角的进动角α和章动角β,转换公式为
| $\alpha =\arctan (j_{T}^{B}/i_{T}^{B}),\beta =\arccos (k_{T}^{B}).$ |
刀头点在定平台坐标系下的位姿为
| $\left[ \begin{matrix} x_{T}^{S} \\ y_{T}^{S} \\ z_{T}^{S} \\ \alpha \\ \beta \\ \end{matrix} \right]=\left[ \begin{matrix} x_{{{O}_{M}}}^{S}-{{l}_{T}}\cos \alpha \sin \beta \\ y_{{{O}_{M}}}^{S}-{{l}_{T}}\sin \alpha \sin \beta \\ z_{{{O}_{M}}}^{S}-{{l}_{T}}\cos \beta \\ \alpha \\ \beta \\ \end{matrix} \right].$ |
式中lT为刀头点到动平台中心的距离.
在混联机床中沿机床坐标系ZB轴方向,并联部分和串联部分存在耦合,为了保证机构运动的稳定性及机构的刚度,本文限定动平台中心到定平台中心的距离为定值,即zOMS=-dC,故串联机构dx、dy、dz的移动分量分别为
| $\begin{align} & {{d}_{x}}=x_{T}^{B}-x_{T}^{S}=x_{T}^{B}+{{l}_{T}}\cos \alpha \sin \beta -x_{{{O}_{M}}}^{S}, \\ & {{d}_{y}}=y_{T}^{B}-y_{T}^{S}=y_{T}^{B}+{{l}_{T}}\sin \alpha \sin \beta -y_{{{O}_{M}}}^{S}, \\ & dz=z_{T}^{B}-z_{T}^{S}=z_{T}^{B}+{{l}_{T}}\cos \beta +{{d}_{C}}+{{d}_{H}}. \\ \end{align}$ |
式中dH为悬臂梁长度.
5 机床干涉校验混联机床受并联机构结构限制,加工过程中可能发生3种类型的干涉:1)并联部分驱动杆与动平台连接处球铰干涉;2)并联部分驱动杆与定平台连接处转动副干涉;3)6路驱动杆约束,如图 1所示.
5.1 球铰干涉校验并联机构由于结构的限制,球铰副转角必须限定在一定范围内:
| ${{\theta }_{Sq}}=\arccos \left( \frac{-w\cdot B_{q}^{S}A_{q}^{S}}{\left| B_{q}^{S}A_{q}^{S} \right|} \right),{{\theta }_{S\min }}\le {{\theta }_{Sq}}\le {{\theta }_{S\max }}.$ |
式中:w为并联机构动平台姿态向量;BSqASq为并联机构第q根驱动杆的杆长向量;θSmin为球铰允许的最小角度,θSmax为球铰允许的最大角度;q=1,2,3.
5.2 转动副干涉校验并联机构由于结构的限制,转动副转角必须限定在一定范围内:
| $\begin{matrix} {{\theta }_{Mq}}=\arccos \left( \frac{{{O}_{S}}A_{q}^{S}\cdot B_{q}^{S}A_{q}^{S}}{\left| {{O}_{S}}A_{q}^{S} \right|\cdot \left| B_{q}^{S}A_{q}^{S} \right|} \right), \\ {{\theta }_{M\min }}\le {{\theta }_{Mq}}\le {{\theta }_{M\max }}. \\ \end{matrix}$ |
式中:OSASq为定平台转动副在定平台坐标系下的向量;θMmin为转动副允许的最小角度,θMmax为转动副允许的最大角度;q=1,2,3.
5.3 杆长约束混联机构杆长必须在给定杆长范围之内:
| ${{l}_{\min }}\le {{l}_{q}}\le {{l}_{\max }}.$ |
式中:l
根据上面干涉校验算法对刀位数据逐行进行校验,一旦发生干涉则终止对刀位数据的处理,并且显示发生干涉的类型和刀位点,通过对发生干涉的类型及刀位点研究确定是否能够通过调整工件坐标系的位姿来适应加工要求;然后,再对混联机床各杆的输入速度和加速度分别校验,使机床在合适的速度和加速度内运行,一旦超过允许的最大速度或加速度,系统将自动调整到合适的加工状态. 通过该方法既能保证机床的效率和加工精度,也能保证机床在运行过程中的安全性.
6 加工实例XYZ-3RPS混联机床的结构参数如下:rM=140 mm,rS=280 mm,dC=384.5 mm,dH=735 mm,lT=124 mm,工件坐标系在机床坐标系下的位置为(890 mm,435 mm,-396 mm),姿态与机床坐标系相同.
在已知机床参数的情况下要完成曲面加工实验,首先使用CAD/CAM软件建立叶片和球面三维模型并生成刀位数据,然后按照给定的工件坐标系定位方法确定工件坐标系的位姿,最后将刀位数据信息转换为6路驱动杆长,并且进行干涉校验. 利用文中给出的控制算法开发后置处理系统,并加工叶片和球面,如图 4所示. 由图 4可知,混联机床刀头点所走过的轨迹与CAM仿真走过的刀具轨迹相重合,并且加工过程中刀具在不同位置时的姿态与仿真时对应刀具位姿相同. 图 4中(b)图给出了叶片曲面数控加工的部分刀位数据,如表 1所示;经过后置处理后得到混联机床对应的驱动杆长,如表 2所示.

|
(a) XYZ - 3RPS 混联机床 (b) 叶片加工 (c) 球面加工 图 4 加工实验 |
| 表 1 刀位数据(部分) |
| 表 2 混联机床驱动杆长(部分) |
1)本文结合Euler角旋转矩阵和混联机床的结构特点,解决了3RPS并联机构参数间的耦合问题,且能够通过给定的刀具位姿快速地获取混联机床的驱动杆长,实用性较强.
2)在笛卡尔坐标系下,利用双直线插补的方法对刀位数据文件密集化处理,使混联机床得到较好的刀具运动轨迹,满足机床加工要求.
3)利用向量法能够快速检测混联机床加工过程中机床的干涉问题,保证机床刀具在自身工作空间内运动,且方法简单.
4)机床加工实验表明算法的可行性,可应用在其他类型的混联机床. 该方法使用C++语言对后置处理进行模块化设计,增大了机床数控系统的开放性,有利于混联机床的推广.
| [1] |
LIU K, FITZGERALD J M, LEWIS F L. Kinematic analysis of a stewart platform manipulator[J].
IEEE Transactions on Industrial Electronics,1993, 40 (2) : 282-293.
( 0) 0)
|
| [2] |
HU Bo, LU Yi, TAN Qing, et al. Analysis of stiffness and elastic deformation of a 2 (SP+SPR+SPU) serial-parallel manipulator[J].
Robotics and Computer-Integrated Manufacturing,2011, 27 (2) : 418-425.
( 0) 0)
|
| [3] |
KRATCHMAN L B, BLACHON G S, WITHROW T J, et al. Design of a bone-attached parallel robot for percutaneous cochlear implantation[J].
IEEE Transactions on Biomedical Engineering,2011, 58 (10) : 2904-2910.
( 0) 0)
|
| [4] |
GHERMAN B, PISLA D, VAIDA C, et al. Development of inverse dynamic model for a surgical hybrid parallel robot with equivalent lumped masses[J].
Robotics and Computer-Integrated Manufacturing,2012, 28 (3) : 402-415.
( 0) 0)
|
| [5] |
LU Yi, XU Jiayin, YU Jianping. Simulation of pre-solving active forces of a 4SPS + SPR parallel machine tool in normal machining a 3D free-form surface[J].
The International Journal of Advanced Manufacturing Technology,2010, 46 (1/2/3/4) : 21-30.
( 0) 0)
|
| [6] |
TLUST J, ZIEGERT J, RIDGEWAY S. Fundamental comparison of the use of serial and parallel kinematics for machines tools[J].
CIRP Annals-Manufacturing Technology,1999, 48 (1) : 351-356.
( 0) 0)
|
| [7] |
孙哲, 赵庆志, 王友林. 基于刀具矢量的并联机床插补研究[J].
山东理工大学学报(自然科学版),2011, 25 (3) : 82-85.
( 0) 0)
|
| [8] |
CHEN S, CHANG T, INASAKI I, et al. Post-processor development of a hybrid TRR-XY parallel kinematic machine tool[J].
The International Journal of Advanced Manufacturing Technology,2002, 20 (4) : 259-269.
( 0) 0)
|
| [9] |
BRISAN C, CSISZAR A. Computation and analysis of the workspace of a reconfigurable parallel robotic system[J].
Mechanism and Machine Theory,2011, 46 (11) : 1647-1668.
( 0) 0)
|
| [10] |
JUNG Y H, LEE D W, KIM J S, et al. NC post-processor for 5-axis milling machine of table-rotating/ tilting type[J].
Journal of Materials Processing Technology,2002, 130 (2) : 641-646.
( 0) 0)
|
| [11] |
陈辉, 王知行, 卓桂荣, 等. 基于UG/ POST 的并联机床数控后置处理器的开发[J].
哈尔滨理工大学学报,2002, 7 (5) : 83-86.
( 0) 0)
|
| [12] |
陈修龙, 赵永生, 鹿玲. 面向并联机床的后置处理方法[J].
计算机集成制造系统,2005, 11 (2) : 257-264.
( 0) 0)
|
| [13] |
李铁民, 郑浩峻, 汪劲松, 等. 并联机床后置处理算法与系统[J].
机械工程学报,2002, 38 (12) : 44-48.
( 0) 0)
|
| [14] |
王旭. 五轴数控机床后置处理算法研究[J].
航空制造技术,2014 (22) : 56-59.
( 0) 0)
|
| [15] |
黄鹏, 王立平, 关立文, 等. 基于Lex 和Yacc 的开放式并联机床后置处理系统开发[J].
高技术通讯,2011, 21 (3) : 303-308.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


