2. 西安理工大学 机械与精密仪器工程学院, 西安 710048
2. School of Mechanical Instrumental Engineering, Xi’an University of Technology, Xi’an 710048, China
指尖密封作为一种柔性密封,具有较优性价比,因而近年来得到了较多的关注和研究[1-2]. 泄漏与磨损是影响指尖密封工作性能的主要因素,迄今有关其性能的研究大多集中在这两个方面. Proctor等[3]通过试验研究,分析不同工况条件对指尖密封性能的影响. Arora等[4-5]通过在低压指尖片和后挡板之间开设压力平衡腔,达到降低指尖密封泄漏的目的,并通过试验进行了验证. Gibson等[6]提出建立新的轴向指尖片中指尖梁结构刚度组合,以达到减小指尖密封泄漏和磨损的目的. Braun等[7]将流体动压指尖密封等效为集中质量-弹簧-阻尼系统,并采用该模型分析了流体动压指尖密封随同转子运动的过程. 近年来还出现了将C/C复合材料应用于指尖密封的相关研究[8]. Chen等[9-10]建立了多层指尖片叠置指尖密封分布质量等效动力学模型,进行了指尖密封动态位移响应分析. 在此基础上,Chen等进一步采用该模型分析了2.5维C/C复合材料指尖密封的动态性能. 对于航空发动机而言,其复杂的运行状态必然会对所处其中的密封装置性能产生重要影响,因而有必要开展这一方面的研究.
本文采用分布质量等效动力学模型,进行了考虑装配条件的C/C复合材料指尖密封动态性能研究,重点分析了不同装配条件下指尖密封泄漏和磨损性能的差异,为工程中选择指尖密封装配类型提供了理论依据.
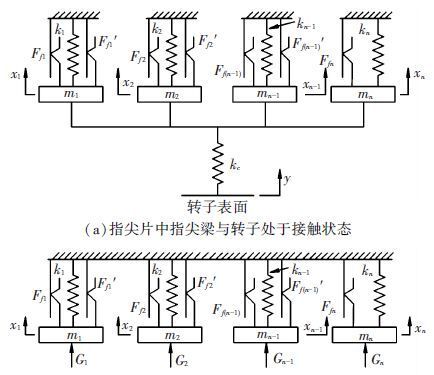
1 指尖密封等效动力学模型 1.1 指尖密封的等效动力学模型多层叠置指尖密封与转子之间的力学行为可以用图 1所示的分布质量等效动力学模型描述. 考虑到指尖密封具有循环对称结构,可以选取指尖片中单一指尖梁作为研究对象. 图中mi和ki分别为第i层指尖片中单一指尖梁的等效质量和等效结构刚度系数;Ffi和F′fi为相邻指尖片(或后挡板)作用于第i层指尖片的摩擦阻力;xi为第i层指尖片中指尖梁的位移响应. 图 1(a)描述了指尖梁与转子处于接触状态的情况, kci为第i层指尖片中单一指尖梁与转子之间的接触刚度,y为转子位移激励. 图 1(b)描述了指尖梁与转子处于脱离状态的情况,此状态下指尖梁与转子之间有泄漏间隙,故而存在着流体压力作用, 用Gi表示作用于第i层指尖片中指尖梁上的间隙流体压力. 图 1(a)和图 1(b)所示指尖密封系统均有阻尼强迫振动.
|
图 1 指尖密封分布质量等效动力学模型 |
指尖梁与转子处于接触状态的有阻尼强迫振动微分方程为
| $\left\{ \begin{align} & {{m}_{1}}{{{\ddot{x}}}_{1}}=-{{k}_{1}}{{x}_{1}}+{{k}_{c1}}\left( {{y}_{1}}-{{x}_{1}} \right)+F_{f1}^{'}-{{F}_{f1}}, \\ & {{m}_{2}}{{{\ddot{x}}}_{2}}=-{{k}_{2}}{{x}_{2}}+{{k}_{c2}}\left( {{y}_{2}}-{{x}_{2}} \right)+F_{f2}^{'}-{{F}_{f2}}, \\ & \vdots \\ & {{m}_{n-1}}{{{\ddot{x}}}_{n-1}}=-{{k}_{n-1}}{{x}_{n-1}}+{{k}_{c\left( n-1 \right)}}\left( {{y}_{n-1}}-{{x}_{n-1}} \right)+ \\ & F_{f\left( n-1 \right)}^{'}-{{F}_{f\left( n-1 \right)}}, \\ & {{m}_{n}}{{{\ddot{x}}}_{n}}=-{{k}_{n}}{{x}_{n}}+{{k}_{cn}}\left( {{y}_{n}}-{{x}_{n}} \right)+-{{F}_{fn}}. \\ \end{align} \right.$ | (1) |
指尖梁与转子处于脱离状态的有阻尼强迫振动微分方程为
| $\left\{ \begin{align} & {{m}_{1}}{{{\ddot{x}}}_{1}}=-{{k}_{1}}{{x}_{1}}+{{G}_{1}}+F_{f1}^{'}-{{F}_{f1}}, \\ & {{m}_{2}}{{{\ddot{x}}}_{2}}=-{{k}_{2}}{{x}_{2}}+{{G}_{2}}+F_{f2}^{'}-{{F}_{f2}}, \\ & \vdots \\ & {{m}_{n-1}}{{{\ddot{x}}}_{n-1}}=-{{k}_{n-1}}{{x}_{n-1}}+{{G}_{n-1}}+F_{f\left( n-1 \right)}^{'}-{{F}_{f\left( n-1 \right)}}, \\ & {{m}_{n}}{{{\ddot{x}}}_{n}}=-{{k}_{n}}{{x}_{n}}+{{G}_{n}}+-{{F}_{fn}}. \\ \end{align} \right.$ | (2) |
分布质量等效动力学模型将指尖片中单一指尖梁等效为一个集中质量,从而将多层叠置指尖密封等效为一个分布质量等效系统. 根据等效质量的动能与指尖梁和指尖靴质量的动能之和相等的原则,推得等效质量 mi的计算公式为
| ${{m}_{i}}={{m}_{f}}+\int_{0}^{l}{\left( \rho h\delta \right){{x}^{2}}\left( z \right)dz.}$ |
式中: mf为指尖靴质量,l为指尖梁长度,ρ为C/C复合材料密度,h为指尖梁宽度,δ为指尖片厚度,x(z)为指尖梁上任意质点的静位移.
1.2.2 等效结构刚度系数在指尖靴上施加径向载荷,通过有限元计算受力后的指尖靴位移,将径向载荷与指尖靴位移的比值作为指尖密封等效结构刚度. 有限元计算需要知道C/C复合材料的弹性常数,考虑到C/C复合材料的宏观表现为正交各向异性,故采用平均刚度法计算C/C复合材料弹性常数,如表 1所示.
| 表 1 2.5 维C/C复合材料的弹性常数 |
指尖梁与转子之间的接触是两个粗糙表面之间的接触,可将其转化为一个刚性光滑表面与一个粗糙弹性表面的接触问题加以处理. 假设在法向载荷作用下所有粗糙峰变形均为弹性变形, 则第i层指尖片中指尖梁与转子之间的接触载荷Pi(d)可以表示为[12]
| ${{P}_{i}}\left( d \right)=\frac{4}{3}{{\rho }_{r}}{{A}_{i}}{{R}^{1/2}}\int_{d}^{\infty }{{{\left( z-d \right)}^{3/2}}\varphi \left( z \right)dz.}$ |
式中: φ(z)为粗糙峰高度分布函数,ρr为粗糙峰密度,Ai为第i层指尖片中指尖梁与转子之间的接触面积,E为当量弹性模量,R为粗糙峰平均当量曲率半径,d为转化粗糙表面与光滑表面之间的平均间隔,z为粗糙峰高度.
根据Shi和Zhao等[13-14]的试验研究, 可以获得转子表面(或指尖靴表面)的平均曲率半径Rj及粗糙峰密度ρrj与表面算术平均粗糙度Raj的关系
| $\begin{align} & {{R}_{j}}=1.1226R_{aj}^{2}+8.81421{{R}_{aj}}+2.97503, \\ & {{\rho }_{rj}}=20268.09716R_{aj}^{2}-102485.71101{{R}_{aj}}+ \\ & 134154.41148. \\ \end{align}$ |
对于给定的平均间隔 d,将第i层指尖片中指尖梁与转子之间的接触载荷Pi(d)和粗糙峰接触平均变形量之比定义为第i层指尖片中指尖梁与转子之间的接触刚度,其表达式为
| ${{k}_{ci}}={{P}_{i}}\left( d \right)/\left[ \frac{1}{{{N}_{i}}\left( d \right)}\sum\limits_{i=1}^{{{N}_{i}}\left( d \right)}{\left( {{z}_{i}}-d \right)} \right].$ |
式中:zi为参与接触的各粗糙峰高度,Ni(d)为参与接触的粗糙峰数.
1.2.4 指尖密封系统的摩擦阻力密封系统高压腔气体作用使得指尖密封后挡板与指尖片之间和指尖片与指尖片之间产生接触压力,当指尖梁有径向运动时,其间产生阻碍指尖梁径向变形的摩擦阻力.
后挡板与第1层指尖片之间的摩擦阻力和第 i层指尖片与第i+1层指尖片之间的摩擦阻力可以统一表示为
| ${{F}_{f\left( i+1 \right)}}=\left\{ \begin{matrix} {{F}_{s\left( i+1 \right)}}sgn \left( {{F}_{i+1}} \right), & \left| {{F}_{i+1}} \right|\ge {{F}_{s\left( i+1 \right)}},\left| \Delta {{{\dot{x}}}_{i+1}}\left( t \right) \right|\approx 0; & {} \\ {{F}_{i+1}}, & \left| {{F}_{i+1}} \right|<{{F}_{s\left( i+1 \right)}},\left| \Delta {{{\dot{x}}}_{i+1}}\left( t \right) \right|\approx 0; & \left( 0\le i\le n-1 \right) \\ {{F}_{d\left( i+1 \right)}}sgn \left( \Delta {{{\dot{x}}}_{i+1}}\left( t \right) \right) & 其他. & {} \\ \end{matrix} \right.$ |
式中:$\Delta {{\dot{x}}_{i+1}}\left( t \right)$为第i层与第i+1层指尖片中指尖梁之间的径向速度差,$\Delta {{\dot{x}}_{i}}\left( t \right)$为后挡板和第1层指尖片中指尖梁之间的径向速度差,Fs(i+1)和Fd(i+1)分别为后挡板与第1层指尖片(i=0的状态)、第i层指尖片与第i+1层指尖片之间的静摩擦力和动摩擦力,Fi+1为除摩擦阻力Ff(i+1)外作用于第i+1层指尖片的合力.
1.3 转子的位移激励指尖密封中转子由于加工误差等因素存在不平衡质量,并在工作中引起转子的振动,这里将转子振动特性处理为转子的周期性径向跳动,其对指尖梁的作用则用转子位移激励表征. 结合指尖密封装配条件和转子不平衡质量对转子位移激励的影响,给出转子位移激励表达式为
| ${{y}_{i}}=\Delta r\sin \left( \omega t \right)\pm e.$ |
式中: ω为转子角速度,Δr为转子不平衡质量引起的径向跳动量,t为时间,e表示过盈量或者间隙量,“+”号用于过盈配合,“-”号用于间隙配合.
1.4 指尖梁与转子之间的流体压力当指尖梁与转子之间出现间隙时, 泄漏的流体会对指尖梁产生压力作用,这种压力作用包含流体静压力和动压力,目前还未有合适的方法确定动压力,所以本文中暂忽略了动压力的影响. 这样,有压流体作用于每层指尖片中指尖梁上的流体压力数值上只是与指尖片所处的轴向位置和密封系统压力差有关,如果认为流体压力沿着轴向方向是线性分布的,则作用于第i层指尖片中指尖梁上的流体压力可以表示为
| ${{G}_{i}}={{p}_{L}}+\frac{i-1/2}{n}\Delta p.$ |
式中: pL为密封系统低压一侧的流体压力,Δp为密封上下游压差.
1.5 指尖密封系统的动态性能 1.5.1 指尖密封的泄漏率指尖梁与转子之间的泄漏间隙用指尖梁位移响应与转子位移激励之差表征, 即t时刻第i层指尖片中指尖梁与转子之间的泄漏间隙hi(t)为
| ${{h}_{i}}\left( t \right)={{x}_{i}}\left( t \right)-{{y}_{i}}\left( t \right).$ |
式中: xi(t)和yi(t)分别为t时刻第i层指尖片中指尖梁的位移响应和与之对应的转子位移激励.
指尖密封具有循环对称结构,因此某一指尖梁在一个周期各个时刻点所对应的泄漏间隙即映射出其它指尖梁与转子之间的泄漏间隙. 这样,将第 i 层指尖片中某一指尖梁与转子之间在各个时刻形成的泄漏间隙进行平均,亦是对此层指尖片各个指尖梁与转子之间泄漏间隙进行平均,得到的此层指尖片平均泄漏间隙为
| ${{\bar{h}}_{i}}\left( t \right)=\frac{1}{f}\sum\limits_{i=1}^{f}{{{h}_{i}}\left( {{t}_{0}}+j\Delta t \right).}$ |
式中: t0为初始时刻点,Δt为计算时间步长,f为转子一个运动周期的计算时间步数.
由n 层指尖片构成的指尖密封平均泄漏间隙为
| ${{\bar{h}}_{i}}\left( t \right)=\frac{1}{n}\sum\limits_{i=1}^{n}{{{{\bar{h}}}_{i}}.}$ |
一个运动周期中指尖密封的泄漏率为[15]
| $Q={{\rho }_{a}}\frac{\pi {{D}_{r}}{{{\bar{h}}}^{3}}\Delta P}{12\eta L}.$ |
式中: ρa为流体密度,η为流体动力黏度,L为指尖密封泄漏间隙长度,Dr为转子直径.
1.5.2 指尖梁与转子的接触压力t时刻转子与第i层指尖片中指尖梁发生接触的接触压力计算公式为
| ${{p}_{i}}\left( t \right)={{F}_{i}}\left( t \right)/{{A}_{i}}.$ |
式中 Fi(t)为第i层指尖片的指尖梁与转子接触的作用力,其计算公式为
| ${{F}_{i}}\left( t \right)=\left\{ \begin{matrix} {{k}_{i}}{{x}_{i}}\left( t \right)+{{F}_{fi}}-F_{fi}^{'}, & \left( 1\le i\le n-1 \right); \\ {{k}_{i}}{{x}_{i}}\left( t \right)+{{F}_{fi}}, & \left( i=n \right). \\ \end{matrix} \right.$ |
一个运动周期中第 i 层指尖片的指尖梁与转子接触的平均压力为
| ${{\bar{P}}_{i}}=\frac{1}{f}\sum\limits_{j=1}^{f}{\frac{{{F}_{i}}\left( {{t}_{0}}+j\Delta t \right)}{{{A}_{i}}}.}$ |
本文探讨2.5维C/C复合材料指尖密封的材料参数和装配条件对其性能的影响. 考虑到计算工作量,分析中采用了由9层指尖片组成的指尖密封. 根据表 1和表 2中的数据计算出的等效质量和等效结构刚度系数分别为1.068 2×10-5 kg和22 636.162 4 N/m. 指尖梁与转子的接触刚度需要在接触过程中根据指尖梁与转子的接触状态确定. 在此基础上求解等效动力学微分方程(1) 和(2) ,获得等效质量的位移响应,进而获得C/C复合材料指尖密封的动态性能.
| 表 2 2.5 维C/C复合材料指尖密封结构和工况参数 |
图 2~4分别为指尖梁位移响应、指尖梁与转子之间的泄漏间隙和接触压力随装配条件的关系,图中横坐标θ均为转子转动的角度. 从图 2中可以看出,依间隙装配、无间隙装配和过盈装配的顺序,指尖片中指尖梁位移响应会随之减小,其原因在于,对于间隙装配,只有当转子位移激励大于配合间隙量后才能作用于指尖梁,指尖梁受到的转子位移激励最小;对于过盈装配和无间隙装配,指尖梁在一开始就会受到转子位移激励的作用,前者更是因为指尖梁预先有变形而受到更大的激励作用. 一方面指尖梁所受位移激励越大,则其弹性回弹越大,表现为指尖梁位移响应减小;另一方面间隙的存在也相当于增大了指尖梁的位移响应. 由于第9层指尖片位于高压侧,故指尖梁与转子脱离接触后承受较大流体作用,一方面表现出较大的位移响应,另一方面在稳定运转条件下,特别在间隙配合条件下,高流体压力的扶持作用产生了指尖梁与转子完全脱离的现象,表明间隙装配条件下,高压区域指尖片的指尖梁基本上与转子位移激励无关.

|
图 2 指尖梁位移响应随装配条件的变化 |
|
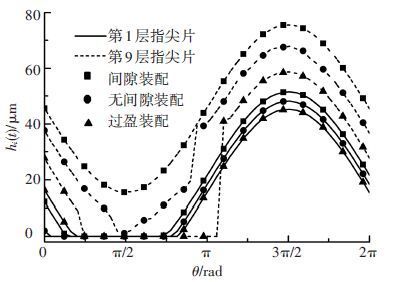
图 3 泄漏间隙随装配条件的变化 |
|
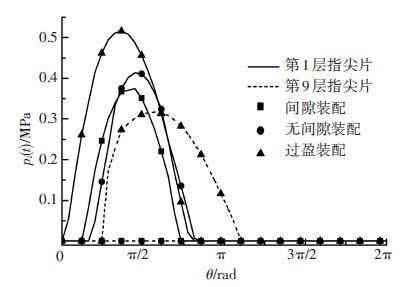
图 4 接触压力随装配条件的变化 |
图 3给出了指尖梁与转子之间泄漏间隙随装配条件的变化. 与图 2的结果相对应,依间隙装配、无间隙装配和过盈装配的顺序,指尖梁与转子之间的泄漏间隙随之减小. 间隙装配条件下,稳定运转后,由于第9层指尖片中指尖梁与转子之间处于完全脱离的状态,故其泄漏间隙也较大.
图 4为指尖梁与转子之间的接触压力随装配条件的变化情况. 依间隙装配、无间隙装配和过盈装配的顺序,指尖梁与转子之间的接触压力随之增大,这一现象产生的原因是显而易见的. 对于间隙装配条件下的第9层指尖片而言,指尖梁与转子之间完全脱离,故其接触压力为0.
不同装配条件下的2.5维C/C复合材料指尖密封平均泄漏间隙和泄漏率见表 3. 如所预料,无论是平均泄漏间隙还是泄漏率,过盈装配条件下的结果均最小.
| 表 3 不同装配条件下的平均泄漏间隙和泄漏率 |
1) 依间隙装配、无间隙装配和过盈装配的顺序,指尖密封平均泄漏间隙和泄漏率均会随之减小,但其接触压力会随之增大,体现出装配类型对指尖密封泄漏与磨损性能贡献的矛盾性. 因此,工程中的指尖密封装配工艺应当视密封部位的主要功能而审慎选择.
2) 过盈装配时,指尖梁与转子之间的接触压力较大,但其泄漏间隙较小,可以通过结构设计减小指尖梁结构刚度,以达到降低指尖密封磨损的目的;间隙装配时,指尖梁与转子之间的接触压力较小,但其泄漏间隙较大,可以通过结构设计增大指尖梁结构刚度,以达到降低其泄漏的目的. 因而,根据指尖密封具体的装配状态,通过结构设计对指尖梁结构刚度进行相应的调整,可以使指尖密封的泄漏和磨损均达到最优.
另外,本文提出的指尖密封动态性能分析方法还存在一些不足,需要在今后的工作中予以关注,例如在确定泄漏间隙流体对指尖梁压力作用时需要考虑流体的动压力等等.
| [1] |
DELGADO I R, PROCTOR M P. Continued investigation of leakage and power loss test results for competing turbine engine seals[C]//AIAA 42nd Joint Propulsion Conference. Reston: AIAA, 2006: 4335-4348.
( 0) 0)
|
| [2] |
DU Kaibing, LI Yongjian, SUO Shuangfu, et al. Dynamic leakage analysis of noncontacting finger seals based on dynamic model[J].
Journal of Engineering for Gas Turbines and Power,2015, 137 (9) : 1-7.
( 0) 0)
|
| [3] |
PROCTOR M P, DELGADO I R. Leakage and power loss test results for competing turbine engine seals: NASA/TM-2004-213049[R]. VIENNA: Glenn Research Center, 2004.
( 0) 0)
|
| [4] |
ARORA G K. Dual pressure balanced non-contacting finger seal: US6364316[P]. 2002-04-02.
( 0) 0)
|
| [5] |
ARORA G K, PROCTOR M P, STEINETZ B M, et al. Pressure balanced, low hysteresis, finger seal test results: NASA/TM-1999-209191[R]. LOS ANGELES: Glenn Research Center, 1999.
( 0) 0)
|
| [6] |
GIBSON N E, TAKEUCHI D, HYNES T, et al. Second generation air-to-air mechanical seal design and performance[R]. SAN DIEGO: Honeywell International, 2011:AIAA Paper 2011-5636.
( 0) 0)
|
| [7] |
BRAUN M J, PIERSON H M, DENG D F, et al. Structure and dynamic consideration towards the design of padded finger seal[R]. HUNTSVILLE: University of Akron, 2003: AIAA Paper 2003-4698.
( 0) 0)
|
| [8] |
路菲, 陈国定, 苏华, 等. 2.5D碳/碳复合材料指尖密封动态性能分析[J].
航空学报,2013, 34 (11) : 2616-2625.
( 0) 0)
|
| [9] |
CHEN Guoding, LU Fei, YU Qiangpeng, et al. Dynamic analysis of finger seal using equivalent model based on distributed mass method[J].
Journal of Mechanical Engineering Science,2014, 288 (16) : 2992-3005.
( 0) 0)
|
| [10] |
CHEN Guoding, WANG Lina, YU Qiangpeng, et al. Dynamic analysis of C/C composite finger seal[J].
Chinese Journal of Aeronautics,2014, 27 (3) : 745-758.
( 0) 0)
|
| [11] |
MARIE H. A study of non-contacting passive-adaptive turbine finger seal performance[D]. Akron: The University of Akron, 2005.
( 0) 0)
|
| [12] |
POLYCARPOU A A, ETSION I. Analytical approximations in modeling contacting rough surfaces[J].
Journal of Tribology, Transactions of the ASME,1999, 121 (2) : 234-239.
( 0) 0)
|
| [13] |
SHI X, POLYCARPOU A A. Measurement and modeling of normal contact stiffness and contact damping at the meso scale[J].
Journal of Vibration and Acoustics, Transactions of the ASME,2005, 127 (1) : 52-60.
( 0) 0)
|
| [14] |
ZHAO Bin, ZHANG Song, MAN Jia, et al. A modified normal contact stiffness model considering effect of surface topography[J].
Journal of Engineering Tribology,2015, 299 (6) : 677-688.
( 0) 0)
|
| [15] |
林基恕.
航空发动机设计手册: 第12册. 传动及润滑系统[M]. 北京: 航空工业出版社, 2002 : 212 -213.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


