单螺母滚珠丝杠副广泛应用于机械产品的进给系统,尤其是数控机床的进给系统. 单螺母滚珠丝杠副的轴向接触刚度是数控机床进给系统中刚度最为薄弱的环节. 为提高数控机床的加工精度,就需要对单螺母滚珠丝杠副静刚度的可靠性及灵敏度进行深入的研究,并对相应的技术参数加以改进. 目前,对于滚珠丝杠副的刚度问题研究报道文献较多. Nakashima等[1]和Takafuji等[2]给出了单螺母滚珠丝杠副接触变形的理论模型;Mei等[3]分析并优化了滚珠丝杠副几何误差对滚珠受载的影响. 吉林大学谭庆昌教授等[4]对机床传动的丝杠进行了动力学分析,建立了滚珠丝杠副传动系统的动力学方程. 南京理工大学的冯虎田教授等[5]分析研究了滚珠丝杠副的载荷对滚珠丝杠副刚度的影响情况,并对滚珠丝杠滚道误差进行了测量和分析. 虽然单螺母滚珠丝杠副静刚度的研究已经取得了较多的成果,但对于单螺母滚珠丝杠副静刚度的可靠性及灵敏度分析还鲜有报道,而单螺母滚珠丝杠副静刚度的研究对于进给系统可靠性和数控机床精度的提升具有重要的作用. 为此,本文开展了单螺母滚珠丝杠副静刚度的可靠性及可靠性灵敏度研究.
本文基于赫兹接触理论建立单螺母滚珠丝杠副轴向接触变形与滚珠丝杠副技术参数的理论模型,利用改进一次二阶矩法计算单螺母滚珠丝杠副的可靠度并求解可靠性灵敏度[6-8]. 通过计算灵敏度,能够分析滚珠丝杠副各技术参数对滚珠丝杠副可靠性的影响.
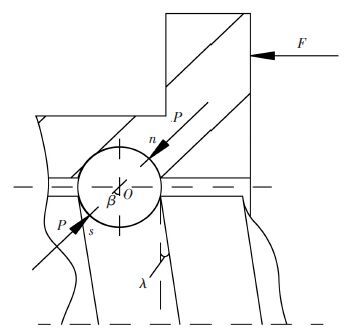
1 轴向接触变形模型单螺母滚珠丝杠副主要由丝杠、螺母、滚珠、滚珠循环返回装置组成[9]. 滚珠丝杠副的技术参数较多,这些参数影响了滚珠丝杠副的可靠度. 其中 λ 为滚珠丝杠副螺旋角, z 为工作滚珠数, β 为接触角, d0 为公称直径, db 为滚珠直径, E′ 为当量弹性模量, F 为工作载荷, ρsp 为滚珠与丝杠滚道面接触点处主曲率和, ρnp 为滚珠与螺母滚道面接触点处主曲率和, esp,masp 为赫兹理论求解中与 ρsp 相关的系数, enp,manp 为赫兹理论求解中与 ρnp 相关的系数, K(enp) 为与椭圆偏心率 enp 有关的第一类完全椭圆积分, K(esp) 为与椭圆偏心率 esp 有关的第一类完全椭圆积分. 单螺母滚珠丝杠副的受力简图如图 1所示.
|
图 1 滚珠丝杠副受力 |
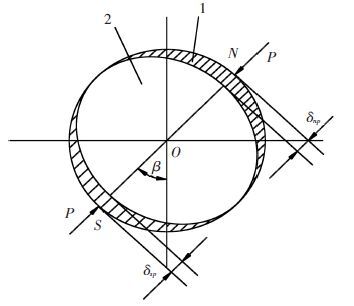
滚珠丝杠副中滚珠的受力变形如图 2所示. 其中1为滚珠受力前的形状,2为滚珠受力后的形状. 阴影部分表示在法向力 P 的作用下,滚珠与丝杠滚道面、螺母滚道面接触点所产生的接触变形分别为 δsp 和 δnp, 则螺母滚道面与丝杠滚道面间由于法向弹性接触变形所产生的法向弹性位移量 δn为
| ${{\delta }_{n}}={{\delta }_{sp}}+{{\delta }_{np}}.$ |
|
图 2 滚珠受力变形 |
螺母滚道面与丝杠滚道面间的法向弹性位移,会在轴线方向上相对于丝杠产生轴向弹性变形量,设其值为 δa. 根据图 1所示几何关系得
| ${{\delta }_{a}}=\frac{{{\delta }_{n}}\cos \lambda }{\sin \beta }.$ |
由滚珠丝杠副的结构特点可知,滚珠中心点的运动轨迹为螺旋线,利用微分几何中的Frenet标架可最终求得 N、S 点的主曲率和分别是
| $\sum{{{\rho }_{np}}=\frac{4}{{{d}_{b}}}}-\frac{2}{t{{d}_{b}}}-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta },$ | (1) |
| $\sum{{{\rho }_{np}}=\frac{4}{{{d}_{b}}}}-\frac{2}{t{{d}_{b}}}+\frac{2\cos \lambda \cos \beta }{{{d}_{0}}-{{d}_{b}}\cos \beta }.$ | (2) |
根据滚珠丝杠副的基本结构可得出
| $\lambda =arctan\frac{{{P}_{h}}}{\pi {{d}_{0}}}.$ |
为简化方程,设
| $\begin{align} & {{K}_{1}}=\frac{2K\left( {{e}_{np}} \right)}{\pi {{m}_{anp}}},{{K}_{2}}=\frac{2K\left( {{e}_{sp}} \right)}{\pi {{m}_{asp}}}, \\ & Q=\frac{1}{8}{{\left( \frac{3}{E\prime } \right)}^{2}}, \\ \end{align}$ |
由赫兹接触理论和单螺母滚珠丝杠副的受力情况[10]可知,在弹性范围内滚珠丝杠副的轴向接触变形量 δa 与其基本参数的关系为
| ${{\delta }_{a}}={{\left( \frac{\cos \lambda }{{{z}^{2}}{{\sin }^{5}}\beta } \right)}^{\frac{1}{3}}}\left( {{K}_{1}}\sqrt[3]{Q\sum{{{\rho }_{np}}}}+{{K}_{2}}\sqrt[3]{Q\sum{{{\rho }_{np}}}} \right){{F}^{\frac{2}{3}}}.$ | (3) |
式(3) 为求解单螺母滚珠丝杠副轴向接触刚度的理论模型. 由式(3) 可知,滚珠丝杠副在工作载荷的作用下,滚珠与丝杠滚道面之间、滚珠与螺母滚道面之间会产生一定的弹性接触变形量.
2 可靠性分析 2.1 单螺母滚珠丝副可靠度分析设在数控机床加工满足精度要求的条件下,滚珠丝杠副的允许轴向接触变形量为 δ,则功能函数Z的表达式为
| $Z=gx\left( X \right)=\delta -{{\delta }_{a}}\left( {{P}_{h}},\beta ,{{d}_{0}},t,F \right).$ | (4) |
其中 X 为导程 Ph、接触角β、工作载荷F、丝杠公称直径d0以及滚道曲率比t组成的随机向量.
设 x*=(Ph*,β*,d0*,t*,F*)T 为极限状态面上一点,即式(4) 满足
| $gx\left( {{x}^{*}} \right)=\delta -{{\delta }_{a}}\left( P_{h}^{*},{{\beta }^{*}},d_{0}^{*},{{t}^{*}},{{F}^{*}} \right)=0.$ | (5) |
在点 x* 处将式(4) 按Taylor级数展开并取至一次项, 则功能函数Z的近似表达式ZL为
| ${{Z}_{L}}=gx\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{n}{\frac{\partial gx\left( {{x}^{*}} \right)}{\partial {{X}_{i}}}}\left( {{X}_{i}}-x_{i}^{*} \right).$ |
假设 X 的元素为相互独立的正态分布[11],则单螺母滚珠丝杠副的可靠性指标为
| $\beta =\frac{{{\mu }_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}}=\frac{gx\left( {{x}^{*}} \right)+\sum\limits_{i=1}^{n}{\frac{\partial gx\left( {{x}^{*}} \right)}{\partial {{X}_{i}}}}\left( {{\mu }_{{{X}_{i}}}}-x_{i}^{*} \right)}{{{\left( {{\sum\limits_{i=1}^{n}{\left[ \frac{\partial gx\left( {{x}^{*}} \right)}{\partial {{X}_{i}}} \right]}}^{2}}\sigma _{{{X}_{i}}}^{2} \right)}^{\frac{1}{2}}}}.$ | (6) |
其中 μZL 和 σZL 分别为 ZL 的均值和标准差. 根据式(3)、(4)和(6),可得
| $\begin{align} & {{\mu }_{{{Z}_{L}}}}=\delta -{{\left( \frac{cos~\lambda }{{{z}^{2}}si{{n}^{5}}\beta } \right)}^{\frac{1}{3}}}\left( {{K}_{1}}{{\left( \frac{1}{8}{{\left( \frac{3}{E'} \right)}^{2}}\sum {{\rho }_{np}} \right)}^{\frac{1}{3}}} \right.+ \\ & {{K}_{2}}\left. {{\left( \frac{1}{8}{{\left( \frac{3}{E'} \right)}^{2}}\sum {{\rho }_{np}} \right)}^{\frac{1}{3}}} \right){{F}^{\frac{2}{3}}}+\frac{\partial gx}{\partial \lambda }\left( {{\mu }_{{{P}_{h}}}}-{{P}_{h}}^{*} \right)+ \\ & \frac{\partial gx}{\partial \beta }\left( {{\mu }_{\beta }}-{{\beta }^{*}} \right)+\frac{\partial gx}{\partial {{d}_{0}}}\left( {{\mu }_{{{d}_{0}}}}-{{d}_{0}}^{*} \right)+ \\ & \frac{\partial gx}{\partial t}\left( {{\mu }_{t}}-{{t}^{*}} \right)+\frac{\partial gx}{\partial F}\left( {{\mu }_{F}}-{{F}^{*}} \right), \\ & {{\sigma }_{{{Z}_{L}}}}=\left( {{\left( \frac{\partial gx}{\partial {{P}_{h}}} \right)}^{2}} \right.{{\sigma }^{2}}_{{{P}_{h}}}+{{\left( \frac{\partial gx}{\partial \beta } \right)}^{2}}\sigma _{\beta }^{2}+{{\left( \frac{\partial gx}{\partial {{d}_{0}}} \right)}^{2}}{{\sigma }^{2}}_{{{d}_{0}}}+ \\ & {{\left( \frac{\partial gx}{\partial t} \right)}^{2}}\sigma _{t}^{2}+{{\left. {{\left( \frac{\partial gx}{\partial F} \right)}^{2}}\sigma _{F}^{2} \right)}^{\frac{1}{2}}}. \\ \end{align}$ |
为简化方程,除了求 t 偏导数外,设
| $H=\frac{4}{{{d}_{b}}}-\frac{2}{t{{d}_{b}}},$ |
对载荷 F 求偏导数为
| $\begin{align} & \frac{\partial gx}{\partial F}=\frac{2}{3}{{F}^{-\frac{1}{3}}}{{\left( {{K}_{1}}\left( Q\left. \left( H-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta } \right) \right) \right. \right.}^{\frac{1}{3}}}+ \\ & {{K}_{2}}\left. {{\left( Q\left. \left( H+\frac{2\cos \lambda \cos \beta }{{{d}_{0}}-{{d}_{b}}\cos \beta } \right) \right) \right.}^{\frac{1}{3}}} \right){{\left( \frac{\cos \lambda }{{{z}^{2}}{{\csc }^{-5}}\beta } \right)}^{\frac{1}{3}}}. \\ \end{align}$ |
对滚道曲率比 t 求偏导数为
| $\begin{align} & \frac{\partial gx}{\partial {{d}_{0}}}={{\left( \frac{\cos \lambda }{{{z}^{2}}{{\csc }^{-5}}\beta } \right)}^{\frac{1}{3}}}\left( 2{{t}^{-2}}Q{{K}_{1}}/ \right. \\ & \left( 3{{d}_{b}}{{\left( Q\left( \frac{4}{{{d}_{b}}}-\frac{2}{t{{d}_{b}}}-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta } \right) \right)}^{\frac{2}{3}}} \right.\left. {} \right)+2{{t}^{-2}}Q{{K}_{2}}/ \\ & \left( 3{{d}_{b}}{{\left( Q\left( \frac{4}{{{d}_{b}}}-\frac{2}{t{{d}_{b}}}+\frac{2\cos \lambda \cos \beta }{{{d}_{0}}-{{d}_{b}}\cos \beta } \right) \right)}^{\frac{2}{3}}} \right.\left. \left. {} \right) \right){{F}^{\frac{2}{3}}}. \\ \end{align}$ |
对丝杠公称直径 d0 求偏导数为
| $\begin{align} & \frac{\partial gx}{\partial {{d}_{0}}}={{\left( \frac{\cos \lambda }{{{z}^{2}}{{\csc }^{-5}}\beta } \right)}^{\frac{1}{3}}}\left( \left( \frac{2{{K}_{1}}Q\cos \lambda \cos \beta }{3{{\left( {{d}_{0}}+{{d}_{b}}\cos \beta \right)}^{2}}} \right) \right./ \\ & {{\left( Q\left( H-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta } \right) \right)}^{\frac{2}{3}}}- \\ & \left( \frac{2{{K}_{2}}Q\cos \lambda \cos \beta }{3{{\left( {{d}_{0}}+{{d}_{b}}\cos \beta \right)}^{2}}} \right)/ \\ & \left. {{\left( Q\left( H-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta } \right) \right)}^{\frac{2}{3}}} \right){{F}^{\frac{2}{3}}}. \\ \end{align}$ |
对接触角 β 求偏导数为
| $\begin{align} & \frac{\partial gx}{\partial \beta }=\left( {{K}_{1}} \right.\left( \frac{2\cos \beta cos\lambda }{{{d}_{0}}+{{d}_{b}}\cos \beta }-\frac{2\cos \lambda \cos \beta \sin \beta {{d}_{b}}}{{{\left( {{d}_{0}}+{{d}_{b}}\cos \beta \right)}^{2}}} \right)/ \\ & \left( 3{{\left( Q\left( H-\frac{2\cos \lambda \cos \beta }{{{\left( {{d}_{0}}+{{d}_{b}}\cos \beta \right)}^{2}}} \right) \right)}^{\frac{2}{3}}} \right)- \\ & {{K}_{2}}\left( \frac{2\sin \beta cos\lambda }{{{d}_{0}}-{{d}_{b}}\cos \beta }+\frac{2\cos \beta \cos \lambda \sin \beta {{d}_{b}}}{{{\left( {{d}_{0}}-{{d}_{b}}\cos \beta \right)}^{2}}} \right)/ \\ & \left. \left( 3{{\left( Q\left( H+\frac{2\cos \lambda \cos \beta }{{{\left( {{d}_{0}}-{{d}_{b}}\cos \beta \right)}^{2}}} \right) \right)}^{\frac{2}{3}}} \right) \right)Q\cdot \\ & {{F}^{\frac{2}{3}}}{{\left( \frac{\cos \lambda }{{{z}^{2}}{{\csc }^{-5}}\beta } \right)}^{\frac{1}{3}}}-\frac{5{{F}^{\frac{2}{3}}}\cos \lambda \cot \beta {{\csc }^{5}}\beta }{3{{z}^{2}}\left( \cos \lambda {{\csc }^{5}}\beta \right)/{{\left. {{z}^{2}} \right)}^{\frac{2}{3}}}}\cdot \\ & \left( {{\left( Q\left( H-\frac{2\cos \lambda \cos \beta }{{{d}_{0}}+{{d}_{b}}\cos \beta } \right) \right)}^{\frac{1}{3}}}{{K}_{1}}+ \right. \\ & \left. {{\left( Q\left( H+\frac{2\cos \lambda \cos \beta }{{{d}_{0}}-{{d}_{b}}\cos \beta } \right) \right)}^{\frac{1}{3}}} \right){{K}_{2}}. \\ \end{align}$ |
当求导程 Ph 偏导数时,可在式(5) 基础上设
| $\begin{align} & J={{d}_{0}}-{{d}_{b}}\cos \beta , \\ & M={{d}_{0}}+{{d}_{b}}\cos \beta . \\ \end{align}$ |
则其偏导数为
| $\begin{align} & \frac{\partial gx}{\partial {{P}_{h}}}={{\left( {{K}_{2}}\left( Q\left( H+\frac{2\cos \lambda \cos \beta }{J} \right) \right) \right.}^{\frac{1}{3}}}+ \\ & \left. {{\left( {{K}_{1}}\left( Q\left( H-\frac{2\cos \lambda \cos \beta }{M} \right) \right) \right.}^{\frac{1}{3}}} \right). \\ & \frac{-{{F}^{\frac{2}{3}}}\sin \lambda {{\csc }^{5}}\beta }{3{{z}^{2}}{{\left( \cos \lambda {{\csc }^{5}}\beta /{{z}^{2}} \right)}^{\frac{2}{3}}}}+{{F}^{\frac{2}{3}}}{{\left( \cos \lambda {{\csc }^{5}}\beta /{{z}^{2}} \right)}^{\frac{1}{3}}}. \\ & \left( \frac{-2{{K}_{2}}Q\sin \lambda \cos \beta }{3J{{\left( Q\left( H+2\cos \lambda \cos \beta /J \right) \right)}^{\frac{2}{3}}}} \right.+ \\ & \left. \frac{2{{K}_{1}}Q\sin \lambda \cos \beta }{3M{{\left( Q\left( H-2\cos \lambda \cos \beta /M \right) \right)}^{\frac{2}{3}}}} \right)\left( \frac{\pi {{d}_{0}}}{P_{h}^{2}+{{\left( \pi {{d}_{0}} \right)}^{2}}} \right). \\ \end{align}$ |
由于极限状态方程的非线性程度较低,所以采用改进一次二阶矩方法计算滚珠丝杠各参数的可靠性灵敏度[12],能够得到近似程度很高的结果. 其中单螺母滚珠丝杠副的可靠度为 R,∂R/∂uxi 为随机参数的均值灵敏度, ∂R/∂σxi 为随机参数的标准差灵敏度.
根据可靠性的灵敏度定义和复合函数求导法则,可得基本变量相互独立情况下失效概率对基本变量的可靠性灵敏度为
| $\begin{align} & \frac{\partial R}{\partial {{u}_{{{x}_{i}}}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial {{x}_{i}}}\exp \left[ -\frac{1}{2}\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right) \right], \\ & \frac{\partial R}{\partial {{\sigma }_{{{x}_{i}}}}}=-\frac{{{\sigma }_{{{x}_{i}}}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }\sigma _{{{Z}_{L}}}^{3}}{{\left( \frac{\partial g}{\partial {{x}_{i}}} \right)}^{2}}\exp \left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right]. \\ \end{align}$ |
为求得滚珠丝杠副各参数的灵敏度,可进行如下运算. 对丝杠公称直径 d0 求灵敏度为
| $\frac{\partial R}{\partial {{u}_{{{d}_{0}}}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial {{d}_{0}}}\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right],$ | (7) |
| $\frac{\partial R}{\partial {{\sigma }_{{{d}_{0}}}}}=\frac{-{{\sigma }_{{{d}_{0}}}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }{{\sigma }^{3}}_{{{Z}_{L}}}}{{\left( \frac{\partial g}{\partial {{d}_{0}}} \right)}^{2}}exp\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right].$ | (8) |
对导程 Ph 求灵敏度为
| $\frac{\partial R}{\partial {{u}_{{{P}_{h}}}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial {{P}_{h}}}\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right],$ | (9) |
| $\frac{\partial R}{\partial {{\sigma }_{{{P}_{h}}}}}=\frac{-{{\sigma }_{{{P}_{h}}}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }\sigma _{{{Z}_{L}}}^{3}}{{\left( \frac{\partial g}{\partial {{P}_{h}}} \right)}^{2}}exp\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right].$ | (10) |
对滚道曲率比 t 求灵敏度为
| $\frac{\partial R}{\partial {{u}_{t}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial t}\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right],$ | (11) |
| $\frac{\partial R}{\partial {{\sigma }_{t}}}=\frac{-{{\sigma }_{t}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }\sigma _{{{Z}_{L}}}^{3}}{{\left( \frac{\partial g}{\partial t} \right)}^{2}}exp\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right].$ | (12) |
对接触角 β 求灵敏度为
| $\frac{\partial R}{\partial {{u}_{\beta }}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial \beta }\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right],$ | (13) |
| $\frac{\partial R}{\partial {{\sigma }_{\beta }}}=\frac{-{{\sigma }_{F}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }\sigma _{{{Z}_{L}}}^{3}}{{\left( \frac{\partial g}{\partial \beta } \right)}^{2}}exp\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right].$ | (14) |
对工作载荷 F 求灵敏度为
| $\frac{\partial R}{\partial {{u}_{F}}}=\frac{1}{\sqrt{2\pi }{{\sigma }_{{{Z}_{L}}}}}\frac{\partial g}{\partial F}\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right],$ | (15) |
| $\frac{\partial R}{\partial {{\sigma }_{F}}}=\frac{-{{\sigma }_{F}}{{u}_{{{Z}_{L}}}}}{\sqrt{2\pi }\sigma _{{{Z}_{L}}}^{3}}{{\left( \frac{\partial g}{\partial F} \right)}^{2}}\text{exp}\left[ -\frac{1}{2}{{\left( \frac{{{u}_{{{Z}_{L}}}}}{{{\sigma }_{{{Z}_{L}}}}} \right)}^{2}} \right].$ | (16) |
滚珠丝杠副的螺旋角、接触角、滚珠直径、滚道曲率比、工作载荷等技术参数均服从正态分布,标准差取均值的0.5%. 各随机参数变量的均值和标准差如表 1所示. 滚珠丝杠副的滚珠数 z= 100,滚珠直径 db=3.175 mm,当量弹性模量E′=2.1×1011 Pa, 取系数 K1=0.642 8,K2=0.625 4. 将各参数代入式(1) 和式(2) 可得取系数
| $\sum{{{\rho }_{np}}=617.698},\sum{{{\rho }_{sp}}=695.378.}$ |
| 表 1 丝杠各参数的均值与方差 |
根据数控车床的加工精度可知,数控车床可加工IT7级精度的试件. 对于基本尺寸<3.000 mm的试件标准公差数值为10 μm,因此允许的偏差量为公差值的一半,即为 δ=5 μm. 将丝杠各参数值代入式(6) ,利用改进一次二阶矩的方法进行迭代运算,可最终求得可靠度指标 β 为
| $\beta =5.161.$ |
根据可靠度指标 β 可以得可靠度 R 为
| $R=0.999 999 8.$ |
利用表 1所示的各参数的均值和标准差,以及式(7)~(16),即可求得单螺母滚珠丝杠副各参数的灵敏度指标为
| $\frac{\partial R}{\partial {{\mu }_{Xi}}}=\left( \begin{matrix} \partial R/\partial \mu \left( {{P}_{h}} \right) \\ \partial R/\partial \mu \left( \beta \right) \\ \partial R/\partial \mu \left( {{d}_{0}} \right) \\ \partial R/\partial \mu \left( t \right) \\ \partial R/\partial \mu \left( F \right) \\ \end{matrix} \right)=\left( \begin{matrix} 1.24268\times {{10}^{-5}} \\ 1.472\text{ }14\times {{10}^{-4}} \\ 3.348\text{ }42\times {{10}^{-6}} \\ -2.487\text{ }06\times {{10}^{-5}} \\ -2.383\text{ }22\times {{10}^{-8}} \\ \end{matrix} \right),$ | (17) |
| $\frac{\partial R}{\partial {{\sigma }_{Xi}}}=\left( \begin{matrix} \partial R/\partial \sigma \left( {{P}_{h}} \right) \\ \partial R/\partial \sigma \left( \beta \right) \\ \partial R/\partial \sigma \left( {{d}_{0}} \right) \\ \partial R/\partial \sigma \left( t \right) \\ \partial R/\partial \sigma \left( F \right) \\ \end{matrix} \right)=\left( \begin{matrix} -3.677\text{ }01\times {{10}^{-8}} \\ -6.754\text{ }92\times {{10}^{-4}} \\ -1.628\text{ }50\times {{10}^{-8}} \\ -2.552\text{ }89\times {{10}^{-5}} \\ -5.409\text{ }60\times {{10}^{-8}} \\ \end{matrix} \right),$ | (18) |
从可靠度对随机参数均值灵敏度矩阵式(17) 可以看出,导程 Ph、接触角β、丝杠公称直径d0 的增加会导致单螺母滚珠丝杠趋于更可靠;滚道曲率比 t, 工作载荷 F 数值的增加则导致单螺母滚珠丝杠副趋于不可靠. 其中接触角 β 的增加对提高可靠度影响最大.
从可靠度对随机参数标准差的灵敏度矩阵式(18) 可以看出,所有随机参数标准差的增加可导致单螺母滚珠丝杠副趋于不可靠.
4 结论1) 在满足工艺条件和控制成本的前提下,结合工厂机床加工精度水平,增加导程 Ph、 接触角 β 和丝杠公称直径 d0 设计值,降低滚道曲率比 t 的设计值,并减小各参数的公差值,从而提高单螺母滚珠丝杠副的可靠性. 其中,接触角 β 的设计值和公差值对单螺母滚珠丝杠副的可靠性影响最大,应首先考虑增加其设计值并降低其公差值.
2) 利用改进一次二阶矩法求解单螺母滚珠丝杠副的可靠度并求解各随机参数的可靠性灵敏度. 说明了各尺寸参数变化对于滚珠丝杠副可靠度的影响程度.
3) 本文通过理论分析和实际计算得出了单螺母滚珠丝杠副的可靠度及可靠性灵敏度,为单螺母滚珠丝杠副的可靠性设计提供了理论依据.
| [1] |
NAKASHIMA K, TAKAFUJI K. Stiffness of a pre-loaded ball screw[J].
The Japan Society of Mechanical Engineers,1987, 37 (11) : 1898-1904.
( 0) 0)
|
| [2] |
TAKAFUJI K, NAKASHIMA K. Stiffness of a ball screw with consideration of deformation of the screw, net and screw thread. Preloaded double nut[J].
JSME International Journal. Ser. 3, Vibration, control engineering, engineering for industry,1990, 33 (4) : 620-626.
( 0) 0)
|
| [3] |
MEI X, TSUTSUMI M, TAO T, et al. Study on the load distribution of ball screws with errors[J].
Mechanism and machine theory,2003, 38 (11) : 1257-1269.
( 0) 0)
|
| [4] |
张会端, 谭庆昌, 李庆华. 机床传动丝杠的动力分析[J].
农业机械学报,2009, 40 (9) : 220-226.
( 0) 0)
|
| [5] |
冯虎田, 李春梅, 陶卫军. 滚珠丝杠滚道误差测量与分析算法研究[J].
南京理工大学学报(自然科学版),2010, 34 (5) : 575-580.
( 0) 0)
|
| [6] |
PARK J G, JEONG W B, SEO Y S, et al. Optimization of crank angles to reduce excitation forces and moments in engines[J].
Journal of mechanical science and technology,2007, 21 (2) : 272-281.
( 0) 0)
|
| [7] |
ZHAO Y, ZHANG Y. Reliability design and sensitivity analysis of cylindrical worm pairs[J].
Mechanism and Machine Theory,2014, 82 (1) : 218-230.
( 0) 0)
|
| [8] |
WANG X, ZHANG Y, LI H, et al. Dynamic reliability sensitivity of cemented carbide cutting tool[J].
Chinese Journal of Mechanical Engineering,2014, 27 (1) : 79-85.
( 0) 0)
|
| [9] |
DADALAU A, MOTTAHEDI M, GROH K, et al. Parametric modeling of ball screw spindles[J].
Production Engineering,2010, 4 (6) : 625-631.
( 0) 0)
|
| [10] |
PLOSS H. Preloaded ball screw assembly: 4,369,011[P]. 1983-01-18.
( 0) 0)
|
| [11] |
ZHANG X, ZHANG Y, HAO Q. Correlation failure analysis of an uncertain hysteretic vibration system[J].
Earthquake Engineering and Engineering Vibration,2008, 7 (1) : 57-65.
( 0) 0)
|
| [12] |
吕震宙, 宋述芳, 李洪双, 等.
结构机构可靠性及可靠性灵敏度分析[M]. 北京: 科学出版社, 2009 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


