2. 哈尔滨工程大学 动力与能源工程学院, 哈尔滨 150001
2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
近年来,有限体积法(FVM)被逐渐应用于声学问题,其目的是采用统一方法求解多物理场(如流固声耦合)问题,避免混合方法带来的一系列问题(如收敛困难)[1].Fogarty等[2]尝试将FVM应用于一维、二维周期性材料及随机材料等属性变化剧烈介质中的声传播问题.Del-Pino等[3]利用高阶Lax-Wendroff格式提出高阶FVM,并应用于模拟地球大气中的大尺度声传播问题.宁立方等[4]采用FVM求解流体Navier-Stokes方程,模拟一维谐振管内的非线性驻波.宣领宽等[5]基于非结构四面体网格将FVM应用于求解三维非均匀介质声波动方程,并基于时域脉冲法将其扩展应用于预测消声器的传递损失.目前,基于FVM求解声波动方程的算法主要采用显格式算法[2-5].显格式算法形成的矩阵通常非常稀疏,甚至不需要采用矩阵形式即可求解,其对存储的消耗很低;同时,不需要特定的线性方程组求解器,算法的程序实现比较容易,且计算效率高. 刘恒等[6]指出提高计算效率的重要途径是发展显格式算法;但是,由于稳定性条件的限制,显格式算法需要的时间步长会随着网格的加密而减小,此时会造成显格式算法的计算效率大大降低.隐格式算法的无条件稳定却有可能解决这一问题.
针对声波动方程,本文采用格点型FVM离散其空间项,Newmark格式离散其时间项,算法上采用隐格式算法.模拟平面波的传播,对比分析本文隐格式Newmark算法与文献中显格式中心差分算法的精度、计算消耗、稳定性及边界条件处理正确性.
1 基本方程静态非均匀流体中的声波动方程为
| $\frac{1}{\rho {{c}^{2}}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}=\left( \nabla \cdot \frac{1}{\rho }\nabla p \right).$ | (1) |
式中:∇为梯度算子,ρ为密度,c为声速,p为声压,t为时间.若为均匀介质时,即退化为经典声波动方程.
文中涉及两大类边界条件:(a) 全反射边界条件[7],包含“绝对硬”理想边界Γv与“绝对软”理想边界Γp,可分别表示为∇p·n=0与p=0;(b)一阶吸收边界条件Γb做为对无穷远的近似,表示为[8]
| $\frac{1}{c}\frac{\partial p}{\partial t}+\nabla p\cdot n=0.$ |
本文采用隐格式法求解声波动方程,并与文献[9]的显格式法对比.二者共同点是声波动方程中的空间项都是基于格点型FVM离散,区别在于显格式法中时间项采用中心差分格式离散,显式推进求解离散方程,而隐格式法中时间项采用Newmark格式离散,隐式迭代求解离散方程.式(1)的积分形式为
| ${{\int }_{\Omega }}\frac{1}{\rho {{c}^{2}}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}\text{d}\Omega ={{\int }_{\Omega }}\nabla \cdot \left( \frac{1}{\rho }\nabla p \right)\text{d}\Omega .$ | (2) |
格点型FVM在离散过程中会用到单元的型函数,常见的网格单元形式有三角形、四边形、四面体、三棱柱、六面体[10].本文以二维四边形单元为例.
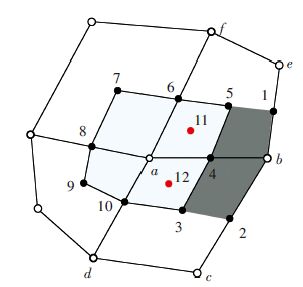
2.1 空间离散图 1为二维声场控制体积示意图,计算域用4节点四边形单元划分.在内部节点a周围建立边界Γint为3-4-5-6-7-8-9-10-3的控制体Ωa,在边界节点b周围建立边界Γint为1-5-4-3-2-b-1的控制体Ωb.密度ρ、声速c定义在单元中心,并假设其在单元内均匀分布;待解变量声压p定义在节点上,并假设在控制体内均匀分布.参考文献[11],假设声压加速度在内部控制体Ωa内均匀分布,式(2)的左端表示为
|
图 1 二维声场控制体积示意 |
| ${{\int }_{\Omega }}\frac{1}{\rho {{c}^{2}}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}\text{d}\Omega =\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}{{\int }_{\Omega }}\frac{1}{\rho {{c}^{2}}}\text{d}\Omega =\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}{{g}_{a}}.$ | (3) |
式中: na为节点a周围单元总数,ρi、ci为节点a周围第i个单元内的密度、声速,(Sa)i为节点a周围第i个单元中参与控制体内的面积,ga为节点a集中属性.
式(2)的右端项采用高斯定理
| $\begin{align} & {{\int }_{\Omega }}\nabla \cdot \left( {{\rho }^{-1}}\nabla p \right)\text{d}\Omega ={{\int }_{{{\Gamma }^{int}}}}{{\rho }^{-1}}\nabla p\cdot n\text{d}\Gamma = \\ & \sum\limits_{i=1}^{{{n}_{a}}}{{{\int }_{\Gamma _{i}^{^{int}}}}}\left( {{\rho }^{-1}}\nabla p\cdot n \right)\text{d}\Gamma . \\ \end{align}$ | (4) |
引入型函数,单元内的压力梯度为
| $\nabla p=\left( \frac{\partial p}{\partial x},\frac{\partial p}{\partial y} \right)=\left( \sum\limits_{j=1}^{4}{\frac{\partial {{N}_{j}}}{\partial x}}{{p}_{j}},\sum\limits_{j=1}^{4}{\frac{\partial {{N}_{j}}}{\partial y}}{{p}_{j}} \right).$ |
式中: N为型函数,∂Nj/∂x、∂Nj/∂y的表达式可参考文献[9-12].
由式(3)、(4),式(2)可变为
| ${{g}_{a}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}=\sum\limits_{i=1}^{{{n}_{a}}}{\int_{\Gamma _{_{i}}^{\text{int}}}{\left( \frac{1}{\rho }\nabla p\cdot n \right)}}\text{d}\Gamma =\sum\limits_{i=1}^{{{n}_{a}}}{\sum\limits_{j=1}^{4}{\left( {{k}_{ij}}{{p}_{ij}} \right)}}.$ | (5) |
式中:下标ij表示节点a周围第i个单元内第j个节点,四边形单元中kij的表达式见2.2节.
在介质边界控制体Ωb上,式(2)可表示为
| ${{g}_{b}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}=\sum\limits_{i=1}^{{{n}_{a}}}{\int_{\Gamma _{_{i}}^{\text{int}}}{\left( \frac{1}{\rho }\nabla p\cdot n \right)}}\text{d}\Gamma +{{\int }_{2-b-1}}\left( \frac{1}{\rho }\nabla p\cdot n \right)\text{d}\Gamma .$ | (6) |
假设为“绝对硬”全反射边界条件,则式(6)右端第二项为零,自然满足.
假设为吸收边界条件Γb,则式(6)右端第二项可表示为
| $\begin{align} & {{\int }_{2-b-1}}\left( \frac{1}{\rho }\nabla p\cdot n \right)\text{d}\Gamma =-{{\int }_{2-b-1}}\left( \frac{1}{\rho c}\frac{\partial p}{\partial t} \right)\text{d}\Gamma = \\ & -\frac{\partial p}{\partial t}{{\int }_{2-b-1}}\left( \frac{1}{\rho c} \right)d\Gamma =-\frac{\partial p}{\partial t}\left( \frac{{{L}_{2-b}}}{{{\left( \rho c \right)}_{3}}}+\frac{{{L}_{b-1}}}{{{\left( \rho c \right)}_{5}}} \right). \\ \end{align}$ | (7) |
式中: L2-b、Lb-1分别为边2-b、b-1的长度,(ρc)3、(ρc)5分别为单元abcd、abef内的密度、声速的乘积.
由式(6)、(7),式(5)可变为
| ${{g}_{b}}\frac{{{\partial }^{2}}p}{\partial {{t}^{2}}}=\sum\limits_{i=1}^{{{n}_{bn}}}{{{k}_{i}}{{p}_{i}}}-\frac{\partial p}{\partial t}\left( \frac{{{L}_{2-b}}}{{{\left( \rho c \right)}_{3}}}+\frac{{{L}_{b-1}}}{{{\left( \rho c \right)}_{5}}} \right).$ |
式中,nbn为节点b周围的节点总数(包含节点b),则
| $G\overset{\cdot \cdot }{\mathop{P}}\,=KP-C\overset{\cdot }{\mathop{P}}\,,$ | (8) |
G、K、C分别为各节点处g、k、∫Γ(ρc)-1dΓ组成的矩阵,$\overset{\cdot \cdot }{\mathop{P}}\,$、$\overset{\cdot }{\mathop{P}}\,$、P分别为各节点处的∂2p/∂t2、∂p/∂t、p组成的列向量.
2.2 四边形单元处理图 2为节点1周围的第i个四边形单元C1234,四边形单元为线性单元,有
| ${{k}_{ij}}=\frac{{{a}_{ij1}}{{\left( {{L}_{ix}} \right)}_{PO}}+{{b}_{ij1}}{{\left( {{L}_{iy}} \right)}_{PO}}+{{a}_{ij4}}{{\left( {{L}_{ix}} \right)}_{OS}}+{{b}_{ij4}}{{\left( {{L}_{iy}} \right)}_{OS}}}{{{\rho }_{i}}}.$ |
式中,ρi为节点1周围第i个四边形单元C1234的密度,且有
| $\begin{align} & {{a}_{ij1}}={{\int }_{a-o}}\frac{\partial {{N}_{j}}}{\partial x}\text{d}\eta ={{\int }^{0}}_{-1}\frac{\partial {{N}_{j}}}{\partial x}\text{d}\eta , \\ & {{b}_{ij1}}={{\int }_{a-o}}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\eta ={{\int }^{0}}_{-1}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\eta , \\ & {{a}_{ij4}}={{\int }_{d-o}}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\xi ={{\int }^{0}}_{-1}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\xi , \\ & {{b}_{ij4}}={{\int }_{d-o}}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\xi ={{\int }^{0}}_{-1}\frac{\partial {{N}_{j}}}{\partial y}\text{d}\xi , \\ & {{\left( {{L}_{ix}} \right)}_{PO}}=-{{\left( {{L}_{ix}} \right)}_{OP}}=0.25\left( {{x}_{3}}+{{x}_{4}}-{{x}_{1}}-{{x}_{2}} \right), \\ & {{\left( {{L}_{iy}} \right)}_{PO}}=-{{\left( {{L}_{iy}} \right)}_{OP}}=0.25\left( {{y}_{3}}+{{y}_{4}}-{{y}_{1}}-{{y}_{2}} \right), \\ & {{\left( {{L}_{ix}} \right)}_{SO}}=-{{\left( {{L}_{ix}} \right)}_{OS}}=0.25\left( {{x}_{2}}+{{x}_{3}}-{{x}_{1}}-{{x}_{4}} \right), \\ & {{\left( {{L}_{iy}} \right)}_{SO}}=-{{\left( {{L}_{iy}} \right)}_{OS}}=0.25\left( {{y}_{2}}+{{y}_{3}}-{{y}_{1}}-{{y}_{4}} \right). \\ \end{align}$ |
式中(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)分别为四边形单元节点1、2、3、4的坐标.

|
图 2 任意四边形单元 |
二阶时间项的离散可采用的隐格式算法有线性加速度法、Newmark法及Houbolt法等. 文献[13]指出,线性加速度法可选择的时间步长较小,而Newmark法的计算精度比Houbolt法高.同时,Newmark法是结构动力学中最流行的一种方法,文献[11]指出,当δ≥0.5,α≥0.25(0.5+δ)2时,Newmark法是无条件稳定的.文献[14]指出当ω0Δt <0.3时(ω0为固有频率对应的角频率),数值阻尼<2%,系统固有频率误差<1%.因此本文尝试采用Newmark法求解二阶时间项,并与格点型FVM相结合,将Newmark法用于求解式(8)
| $\begin{align} & \left( K-1/\left( \alpha \Delta {{t}^{2}} \right)G-\delta /\left( \alpha \Delta t \right)C \right){{P}^{t+\Delta t}}= \\ & -G[1/\left( \alpha \Delta {{t}^{2}} \right){{P}^{t}}+1/{{\left( \alpha \Delta t \right)}^{\dot{P}t}}+ \\ & {{\left( 1/\left( 2\alpha \right)-1 \right)}^{\ddot{P}t}}\left] -C \right[\delta /\left( \alpha \Delta t \right){{P}^{t}}+ \\ & {{\left( \delta /\alpha -1 \right)}^{\dot{P}t}}+\left( \delta /\left( 2\alpha \right)-1 \right)\Delta {{t}^{\ddot{P}t}}]. \\ \end{align}$ | (9) |
依据式(9)可获得节点声压p,节点声压速度、加速度可分别由式(10)、(11)更新:
| $\begin{align} & {{{\ddot{P}}}^{t+\Delta t}}=1/\left( \alpha \Delta {{t}^{2}} \right)\left( {{P}^{t+\Delta t}}-{{P}^{t}} \right)-1/\left( \alpha \Delta t \right){{{\dot{P}}}^{t}}- \\ & \left( 1/\left( 2\alpha \right)-1 \right){{{\ddot{P}}}^{t}}, \\ \end{align}$ | (10) |
| ${{{\dot{P}}}^{t+\Delta t}}={{{\dot{P}}}^{t}}+\left( 1-\delta \right)\Delta t{{{\ddot{P}}}^{t}}+\delta \Delta t{{{\ddot{P}}}^{t+\Delta t}}.$ | (11) |
由式(10)、(11),式(8)可变为以节点声压P为未知量的线性系统,可采用迭代求解器或直接求解器进行求解,本文采用迭代求解器代数多重网格法[15]求解.“绝对软”全反射边界条件,可采用置大数法或置“1”法等[16]进行处理.
3 两种格式比较为方便对比两种格式,研究图 3所示的声学计算域,上下为绝对硬边界Γv,左侧施加高斯压力脉冲
| $p\left( t \right)=\text{exp}\left[ -{{\left( t-3T\prime \right)}^{2}}/{{\left( T\prime \right)}^{2}} \right]\text{P}a.$ |
其中: T′=2.5×10-3 s,声速c=500 m/s,密度ρ=1 kg/m3.

|
图 3 矩形声场计算域 |
表 1中4种均匀分布的四边形单元用于网格无关性分析,时间步长均为Δt=5×10-5 s.监测点M声压的时域响应如图 4所示,Grid 2、Grid 3及Grid 4的结果相互吻合良好,所以当λ/Δx≥10,显格式法与隐格式法均能够获得满足精度要求的解,Grid 3能够用于进一步分析.表 1中给出两种格式的内存和CPU消耗,二者的内存消耗区别不大,但时间步长Δt相同时,显格式消费的CPU时间更少.
| 表 1 计算详细信息 |

|
图 4 不同网格模型点M处声压 |
利用Grid 3分析时间步长对计算结果的影响.表 2中列出两种格式点M声压的峰值误差.针对显格式算法,(c0Δt)/dx=0.98、1.00时,计算结果稳定且吻合良好;当(c0Δt)/dx=1.02>1.00时,计算结果发散,说明显格式算法是条件稳定的,且稳定性条件与文献[10]的推导结果基本一致.针对隐格式算法,ω0Δt=0.1、0.3时,计算结果吻合良好,但ω0Δt=0.50、0.51及0.60时出现明显衰减,其中ω0=2πfmax ′,5种情况下的结果均没有出现发散,表明隐格式算法是无条件稳定的.当ω0Δt=0.3时,相对误差<1%,对应一个周期内21个时间采样点,小于文献[17]中33个时间采样点.当ω0Δt> 0.5时,预测声压级差超过工程上±0.5 dB的误差需求,一个周期内有13个时间采样点.相对误差、绝对误差、声压级差分别由式(12)~(14)计算:
| $相对误差=\left( {{p}^{预测}}-{{p}^{解析}} \right)/{{p}^{解析}}\times 100%$ | (12) |
| $绝对误差=\left| {{p}^{预测}}-{{p}^{解析}} \right|,$ | (13) |
| $声压级差=20\times \text{lg}10\left( {{p}^{解析}}/{{p}^{预测}} \right)$ | (14) |
| 表 2 不同时间步长条件时隐格式的峰值误差 |
基于Grid3,采用3种时间步长,对比隐格式和显格式方法得到点M声压的绝对误差,见图 5.结果表明,基于相同的计算网格和时间步长,隐格式方法得到的结果与精确解吻合更好.

|
图 5 不同时间步长时两种格式绝对误差的比较 |
分析两种方法处理绝对软边界、绝对硬边界、吸收边界的正确性,基于Grid3,时间步长Δt=1.25×10-4 s,右侧边界分别为不同边界条件时点M声压(见图 6).当右侧边界为绝对软边界时,两种格式均存在反相同幅值反射;当右侧边界为绝对硬边界时,两种格式均存在同相同幅值反射;当右侧边界为吸收边界时,均将波成功透射出去.

|
图 6 不同边界条件下点M声压 |
图 7为不同边界条件下点M声压的绝对误差,隐格式算法得到的入射波精度高于显格式算法;对全反射边界条件的处理,显格式算法的精度高于隐格式算法;对吸收边界条件的处理,显格式算法的精度低于隐格式算法.

|
图 7 不同边界条件时两种格式绝对误差的比较 |
1) 讨论了空间步长的影响. 当λ/Δx≥10后,显格式算法与隐格式算法均能够达到满足精度要求的解,并且随着网格的加密,计算结果保持不变;两种格式在内存消耗上比较接近,但在采用相同时间步长的前提下,显格式耗费较少的CPU时间.
2) 讨论时间步长的影响. 显格式算法是条件稳定的,当(c0Δt)/dx≤1.0时,计算结果稳定,而不满足此条件时计算会快速发散,这与理论推导的结果一致. 隐格式Newmark算法是无条件稳定的,当ω0Δt≤0.3时,所预测声压的相对峰值误差<1%,当ω0Δt>0.5时,所预测声压级的相对峰值误差会超出工程上±0.5 dB的误差需求.
3) 对于文中提到的全反射边界和吸收边界条件,两种算法均能够提供峰值误差<2%的数值解;显格式算法所得的入射波精度高于隐格式算法;对全反射边界条件的处理,显格式算法处理的精度高于隐格式算法;对吸收边界条件的处理,显格式算法处理的精度低于隐格式算法.
| [1] |
MANEERATANA K. Development of the finite volume method for non-linear structural applications[D]. London: the University of London, 2000.
( 0) 0)
|
| [2] |
FOGARTY T R, LEVEQUE R J. High-resolution finite-volume methods for acoustic waves in periodic and random media[J].
Journal of the Acoustical Society of America,1999, 106 (1) : 17-28.
( 0) 0)
|
| [3] |
DEL-PINO S, DESPRS B, HAVÉ P, et al. 3D Finite Volume simulation of acoustic waves in the earth atmosphere[J].
Computers & Fluids,2009, 38 (4) : 765-777.
( 0) 0)
|
| [4] |
宁方立, 张文治, 董梁. 圆柱形谐振管内非线性驻波的有限体积计算方法[J].
机械工程学报,2012, 48 (16) : 116-121.
( 0) 0)
|
| [5] |
宣领宽, 张文平, 明平剑, 等. 预测消声器声学性能的时域非结构有限体积法[J].
哈尔滨工程大学学报,2012, 33 (2) : 185-191.
( 0) 0)
|
| [6] |
刘恒, 廖振鹏. 波动数值模拟的一种显式方法——二维波动[J].
力学学报,2010, 42 (6) : 1104-1116.
( 0) 0)
|
| [7] |
杜功焕, 朱哲民, 龚秀芬.
声学基础[M]. 南京: 南京大学出版社, 2001 .
( 0) 0)
|
| [8] |
李太宝.
声场的方程和计算方法[M]. 北京: 科学出版社, 2005 .
( 0) 0)
|
| [9] |
宣领宽, 张文平, 明平剑, 等. 基于不同时间步长时域非结构有限体积法模拟声-弹性耦合问题[J].
固体力学学报,2013, 34 (2) : 158-168.
( 0) 0)
|
| [10] |
TAYLOR G A, BAILEY C, CROSS M. A vertex-based finite volume method applied to non-linear material problems in computational solid mechanics[J].
International Journal for Numerical Methods in Engineering,2003, 56 (4) : 507-529.
( 0) 0)
|
| [11] |
王勖成.
有限单元法[M]. 北京: 清华大学出版社, 2003 .
( 0) 0)
|
| [12] |
宣领宽, 明平剑, 龚京风, 等. 三维各向异性功能梯度材料的有限体积法[J].
哈尔滨工业大学学报,2014, 46 (7) : 95-100.
( 0) 0)
|
| [13] |
赵倩. 新型差分格式TDFEM及其腔体屏蔽效能分析研究[D]. 南京: 南京航空航天大学, 2011.
( 0) 0)
|
| [14] |
GILES M B. Stability and accuracy of numerical boundary conditions in aeroelastic analysis[J].
International Journal for Numerical Methods in Fluids,1997, 24 (8) : 739-757.
( 0) 0)
|
| [15] |
明平剑. 基于非结构化网格气液两相流数值方法及并行计算研究与软件开发[D]. 哈尔滨: 哈尔滨工程大学, 2008.
( 0) 0)
|
| [16] |
李亚智, 赵美英, 万小朋.
有限元法基础与程序设计[M]. 北京: 科学出版社, 2004 .
( 0) 0)
|
| [17] |
倪大明. 非结构化网格FVM在流体动力声学计算中的应用研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


