海量流程资产的有效利用取决于信息系统的流程管理技术水平,而有效的流程相似度查询技术则成为提升业务流程管理水平的关键技术之一[1]. 在相似性计算方面,标注于流程节点上的文本标签的相似度是进行流程相似性分析的基础[2-3]. 传统的基于文本的匹配检索可以用来索引和搜寻业务流程模型知识库. 但这类匹配和检索是以关键词和字符匹配[4-5]或其特征值[6]的近似程度为基础,若模型标记的文本标签包含特定的关键词或字符,那么这种方式是确有成效的[7]. 但是,这种相似的应用没有考虑语义异构性的存在. 这使得采用以关键词和字符匹配为基础的传统流程相似匹配难以实现更加准确的语义查询[8]. 基于语义知识库的语义相似度是一种计算文本与文本间在其概念关联上相似程度的度量方法. 因此,本文引入基于语义知识库的概念相似度计算方法,将其应用在流程匹配中的文本标签的相似度计算中,以提高流程匹配的准确度.
在流程匹配过程的寻优算法上,现存的几种流程匹配算法都具备各自的特点,但在流程节点较多时,都表现出各自的不足. 例如贪婪算法[9],可以在很短时间内得到一个匹配结果以及匹配的相似度值,但很可能得到的不是最优匹配. 而作为典型的启发式算法的A*算法[10],虽然可以确保找到最优解,但其耗时代价可能会随着节点数增加而急剧增长. 因此,本文提出一种基于遗传算法[11-12]的折中优化的算法,旨在节点数较多时,既能在相似度上达到较为满意的值,又可以在匹配寻优过程的时间耗费上处于可以接受的范围.
1 节点语义相似度计算模型 1.1 语义相似度及其关键定义定义1 义原相似度[13]. 设s1与s2为两个义原,义原间距离记为D(s1,s2),相似度记为Ssem(s1,s2), 则
| ${{S}_{\text{sem}}}\left( {{s}_{1}},{{s}_{2}} \right)\frac{\alpha \times \left( {{d}_{1}}+{{d}_{2}} \right)}{\left( D\left( {{s}_{1}},{{s}_{2}} \right)+\alpha \right)\times \max \left( \left( {{d}_{1}}-{{d}_{2}} \right),1 \right)}.$ |
其中:d1和d2 分别是义原s1和义原s2所处的层次,α>0,且α是相似度为0.5时s1和s2之间的距离.
定义2 义原最佳匹配[14]. 设S1={s11,s12,…,s1m} 和S2={s21,s22,…,s2n}分别为包含m和n个义原的集合,且有m≤n. 定义从S1到S2的一个单射集合为M. 则义原的最佳匹配是指一个单射集合Mopt,对于所有其他的单射集合M都有
| $\sum\limits_{\left( {{s}_{1i}},{{s}_{2j}} \right)\in {{M}^{\text{opt}}}}{{{S}_{\text{sem}}}\left( {{s}_{1i}},{{s}_{2j}} \right)}\ge \sum\limits_{\left( {{s}_{1i}},{{s}_{2j}} \right)\in M}{{{S}_{\text{sem}}}\left( {{s}_{1i}},{{s}_{2j}} \right)}.$ |
其中Ssem 为两个义原间的相似度.
定义3 义项相似度. 设C1、C2为两个义项,C1由m 个义原描述s11,s12,…,s1m,C2由n个义原描述s21,s22,…,s2n,且m≤n . Mopt为描述两个义项的义原集合的最佳匹配,则C1、C2 的相似度为[15]
| ${{S}_{\text{Concept}}}\left( {{C}_{1}},{{C}_{2}} \right)=\sum\limits_{\underset{\left( {{s}_{i}},{{s}_{j}} \right)\in {{M}^{\text{opt}}}}{\mathop{i=1}}\,}^{m}{{{w}_{i}}\times {{S}_{\text{sem}}}\left( {{s}_{i}},{{s}_{j}} \right)}.$ |
其中wi是为不同的义原映射赋予的不同权值.
定义4 概念相似度. 设概念S1的名称L1有m个义项C11,C12,…,C1m,概念S2的名称L2有n个义项C21,C22,…,C2n,则概念S1和概念S2的相似度为[16-17]
| $S\left( {{S}_{1}},{{S}_{2}} \right)=\underset{\begin{smallmatrix} i=1\cdots m \\ j=1\cdots n \end{smallmatrix}}{\mathop{\max }}\,\left( {{S}_{\text{concept}}}\left( {{C}_{1i}},{{C}_{2j}} \right) \right).$ |
其中SConcept(C1i,C2j)表示义项C1i、C2j之间的相似度.
1.2 流程节点的语义相似度计算定义5 同义词相似度[18]. 设l1,l2∈Ω为文本标签,W 为所有词语或单词的集合,w∶ Ω→P(W)为分离文本标签为单个词汇集合的函数. s∶W→P(W)可获取给定单词的同义词. 令w1=w(l1),w2=w(l2),设wi和ws 分别为相同词汇和同义词的权值. S(l1,l2)为l1和l2 的语义相似度:
| $\begin{align} & S({{l}_{1}},{{l}_{2}})=[2\cdot {{w}_{i}}\cdot |{{w}_{1}}\cap {{w}_{2}}|+{{w}_{s}}\cdot (|s({{w}_{1}},{{w}_{2}})|+ \\ & |s({{w}_{2}},{{w}_{1}})\left| )]/ \right|{{w}_{1}}+{{w}_{2}}|. \\ \end{align}$ |
其中$s\left( {{w}_{1}},{{w}_{2}} \right)=\underset{w\subseteq {{w}_{1}}-{{w}_{2}}}{\mathop{\cup }}\,s\left( w \right)\cap \left( {{w}_{2}}-{{w}_{1}} \right)$为w2中w1的同义词集合.
定义6 文本标签的语义相似度. 设l1,l2∈Ω为文本标签,W为所有词语或单词的集合,w∶Ω→P(W)为分离文本标签成单词集合的函数. sword 是基于语义知识库的一个词汇相似度函数. 令w1=w(l1),w2=w(l2),M为词汇集合w1与w2的词汇单射集合. Mopt为使得词汇映射相似度值之和最大的映射. S(l1,l2)为文本标签l1和l2的语义相似度,即
| $S\left( {{l}_{1}},{{l}_{2}} \right)=\frac{2}{\left| {{w}_{1}} \right|+\left| {{w}_{2}} \right|}\sum\limits_{\left( {{w}_{1i}},{{w}_{2j}} \right)\in {{M}^{\text{opt}}}}{{{s}_{\text{word}}}\left( {{w}_{1i}},{{w}_{2j}} \right)}.$ |
其中:|w1|、|w2| 分别表示w1和w2中的词汇数,w1i、w2j分别表示w1 和w2 中的一个词语.
定义7 节点特性相似度. 设B1(N1,E1,τ1,λ1,α1)和B2(N2,E2,τ2,λ2,α2)是两个流程图,令n1∈N1 和 n2∈N2分别为B1和B2的一个节点. S为相似度函数. 那么可以定义节点n1和n2特性的相似度为
| ${{S}_{\text{att}}}\left( {{n}_{1}},{{n}_{2}} \right)=\underset{\begin{matrix} \left( {{t}_{1}},{{l}_{1}} \right)\in {{\alpha }_{1}}\left( {{n}_{1}} \right), \\ \left( {{t}_{2}},{{l}_{2}} \right)\in {{\alpha }_{2}}\left( {{n}_{2}} \right), \\ {{t}_{1}}={{t}_{2}} \\ \end{matrix}}{\mathop{{{F}_{AVG}}}}\,S\left( {{l}_{1}},{{l}_{2}} \right).$ |
特性相似度一般与其他相似度结合起来使用.
定义8 节点类型相似度. 设有流程图B1(N1,E1,τ1,λ1,α1)和B2(N2,E2,τ2,λ2,α2),令n1∈N1 和 n2∈N2分别为B1和B2的节点. 令t∶ T×T→[0,1]为节点类型的相似度函数,则
| ${{S}_{\text{typ}}}\left( {{n}_{1}},{{n}_{2}} \right)=t\left( {{\tau }_{1}}\left( {{n}_{1}} \right),{{\tau }_{2}}\left( {{n}_{2}} \right) \right)$ |
为节点类型相似度函数. t是预先定义的. 可选择以下参考定义形式:
| $\eqalign{ & t\left( {{t_1},{t_2}} \right) = \left\{ \matrix{ 1,{\rm{if }}{t_1} = {t_2}; \hfill \cr 0,{\rm{else;}} \hfill \cr} \right. \cr & t\left( {{t_1},{t_2}} \right) = {S_{{\rm{sem}}}}\left( {{t_1},{t_2}} \right). \cr} $ |
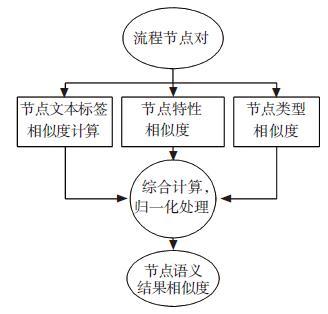
综上,本文设计了如图 1的节点相似度计算模型.
|
图 1 节点相似度计算模型 |
第2种要研究的相似度是业务流程的结构相似度. 结构相似度基于图编辑距离来定义[19] .
定义9 图的编辑距离. 设B1(N1,E1,τ1,λ1,α1)和B2(N2,E2,τ2,λ2,α2)是两个流程图,S为相似度函数,M:(N1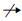
| $\left| {{s}_{n}} \right|+\left| {{s}_{e}} \right|+2\cdot \sum\limits_{\left( n,m \right)\in M}{\left( 1-S\left( n,m \right) \right)}.$ |
图的编辑距离是由两个流程导出的最小化距离. 其计算方法是:1减去“插入”或“删除”节点“插入”或“删除”边集以及“替换”节点平均距离的平均值的分数部分的差.
定义10 图编辑距离相似度. 设B1=(N1,E1,τ1,λ1,α1)和B2=(N2,E2,τ2,λ2,α2)为两个流程图,S为相似度函数,令M∶ (N1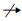
| $\left\{ \begin{align} & {{s}_{\text{ged}}}\left( {{B}_{1}},{{B}_{2}} \right)=1-avg\left( {{s}_{nv}},{{s}_{ev}},{{s}_{bv}} \right), \\ & {{s}_{nv}}=\frac{\left| {{s}_{n}} \right|}{\left| {{E}_{1}} \right|+\left| {{E}_{2}} \right|}, \\ & {{s}_{ev}}=\frac{\left| {{s}_{e}} \right|}{\left| {{E}_{1}} \right|+\left| {{E}_{2}} \right|}, \\ & {{s}_{bv}}=\frac{2\cdot \sum\limits_{\left( n,m \right)\in M}{\left( 1-S\left( n,m \right) \right)}}{\left| {{N}_{1}} \right|+\left| {{N}_{2}} \right|-\left| {{s}_{n}} \right|}. \\ \end{align} \right.$ |
定义11 等价映射和最优等价映射. 设B1(N1,E1,τ1,λ1,α1)和B2(N2,E2,τ2,λ2,α2)为两个流程图,设节点对相似度函数为S∶N1×N2→[0,1]. 一个局部单射MS∶(N1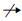
最优等价映射MSopt∶N1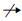
| $\sum\limits_{\left( {{n}_{1}},{{n}_{2}} \right)\in M_{\text{S}}^{\text{OPT}}}{S\left( {{n}_{1}},{{n}_{2}} \right)}\ge \sum\limits_{\left( {{n}_{1}},{{n}_{2}} \right)\in {{M}_{S}}}{S\left( {{n}_{1}},{{n}_{2}} \right)}.$ |
定义12 流程匹配相似度. 设B1=(N1,E1,τ1,λ1,α1)和B2=(N2,E2,τ2,λ2,α2)为两个流程图. 设S为计算两个节点间相似度的函数,且ts 为应忽略的节点类型集合. 设MSopt∶ N1/ N2为通过相似度函数S导出的最优等价映射,其中忽略了ts 中的类型. 那么B1 和B2 间的节点匹配相似度为
| $\begin{align} & {{S}_{\text{nm}}}=\left( 2\cdot \sum\limits_{\left( n,m \right)\in M_{\text{S}}^{\text{opt}}}{S\left( n,m \right)} \right)/ \\ & \left| \left\{ n\left| n\in {{N}_{1}},{{\tau }_{1}}\left( n \right)\notin {{t}_{s}} \right. \right\} \right|+ \\ & \left| \left\{ n\left| n\in {{N}_{2}},{{\tau }_{2}}\left( n \right)\notin {{t}_{s}} \right. \right\} \right|. \\ \end{align}$ |
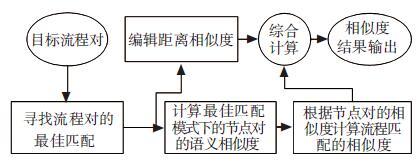
基于以上定义,流程相似度计算模型如图 2.
|
图 2 流程相似度计算模型 |
本文设计了一种基于遗传算法的匹配过程寻优算法,使得计算效率和匹配效果都能满足应用需求. 算法关键设计细节如下.
3.1 流程编码设一个有n 个节点的流程Pn,采用编码1,2,…,n-1,n对每个节点进行编码. 设另一个有m个节点的流程Pm,则其编码为1,2,…,m-1,m. 任意两个流程的节点数总有n≥m. 因为,总可用n表示节点数较多的流程节点数. 当两个节点数分别为n和m的流程Pn和流程Pm进行匹配时,编码的位数便为n,编码每一个基因位上的取值范围是1~n,且每一个基因位上的取值不重复. 编码中每个基因位代表Pn的一个节点,而该基因位的取值代表Pm中的一个节点. 注意到n≥m,因此在基因位的取值中,超过m的值m+1,…,n-1,n是没有意义的. 因此,当某基因位的取值为m+1,…,n-1,n中的一个时,表示该基因位代表的流程Pn的节点不能与Pm中节点匹配.
3.2 种群初始化首先,可以确定一个表示节点间的相似度的矩阵S. 以P9和P7为例,则有相似度矩阵S9×7为
| ${{S}_{9\times 7}}=\begin{matrix} {} & \begin{matrix} 1 & 2 & \cdots & 7 \\ \end{matrix} \\ \begin{matrix} 1 \\ 2 \\ \vdots \\ 9 \\ \end{matrix} & \left[ \begin{matrix} {{S}_{11}} & {{S}_{12}} & \cdots & {{S}_{17}} \\ {{S}_{21}} & {{S}_{22}} & \cdots & {{S}_{27}} \\ \vdots & \vdots & {{S}_{11}} & \vdots \\ {{S}_{91}} & {{S}_{92}} & \cdots & {{S}_{97}} \\ \end{matrix} \right] \\ \end{matrix}$ |
式中,sij为P9的第i个节点和P7中的第j个节点的相似度值.
可以采用贪婪算法生成初始种群. 在上述相似度矩阵S(即S9×7)中,找到值最大的一个sij ,然后,将该值的列号填写到基因位的第一位即得到j,×××××××××,×表示待定. 然后划掉第i行和第j列的所有相似度值,得到一个新的相似度矩阵S′,然后再寻找S′中值最大的元素重复以上过程,直到最后的S′矩阵的列数为0,便得到了一个个体. 如果列数不等于行数,得到的个体可能为(7,3,1,6,2,5,4,××),其中有两个元素不确定. 这时将行中未出现的编号填充上去得到(7,3,1,6,2,5,4,8,9). 此即为贪婪算法的结果. 再对该个体的各个基因位的值做随机变动,或采用变异算子进行变异,可得到初始种群. 利用贪婪算法初始化种群,再通过最优保留的选择策略,保证遗传算法最终的匹配结果一定不差于贪婪算法.
3.3 适应度函数匹配的目标在于求解相似度最大的匹配. 根据定义11中的节点匹配相似度定义,可以将适应度函数设为个体m中所有节点映射相似度之和,因此节点匹配的相似度适应度函数定义如下:
| $f=\sum\limits_{i=1}^{m}{{{s}_{i,m\left( i \right)}}},$ |
其中:m(i)为所求个体第i基因位上的值,si,m(i)为两流程节点相似度矩阵中第i行第m(i)列的值. 求这些匹配上的节点的相似度之和,是最简单的一种适应度函数.
根据流程的结构相似度定义,可以分别得
| $\left\{ \matrix{ \left| {{s_n}} \right| = \sum\limits_{i = 1}^n {{x_i};} \hfill \cr {s_{nv}} = {{\left| {{s_n}} \right|} \over {m + n}}; \hfill \cr {x_i} = \left\{ \matrix{ 1,{\rm{if }}{{\rm{s}}_{i,m\left( i \right)}} > 0; \hfill \cr 0,{\rm{else}}; \hfill \cr} \right. \hfill \cr {s_{ev}} = {{\left| {{s_e}} \right|} \over {\left| {{E_1}} \right| + \left| {{E_2}} \right|}}; \hfill \cr {s_{bv}} = {2 \over {m + n - \left| {{s_n}} \right|}}\sum\limits_{i = 1}^n {{x_i}\left( {1 - {{\rm{s}}_{i,m\left( i \right)}}} \right)} . \hfill \cr} \right.$ |
式中:m(i) 为所求个体第i基因位上的值,si,m(i)为两流程节点相似度矩阵中第i 行第m(i)列的值. 进一步得到结构相似度的适应度函数:
| $f=1-{{F}_{\text{avg}}}\left( {{s}_{nv}},{{s}_{ev}},{{s}_{bv}} \right).$ |
由于采用了非二进制编码,所以变异算子需要采用对应离散数字的变异方法. 在此采用映射互换模式的变异方法、基因段逆转、互换位置相结合的方法进行遗传处理以提高遗传多样性.
3.5 参数设定种群规模根据问题的节点数进行设定. 例如,匹配中,节点较多的流程节点数为n,则相应的种群规模可设为n~2n. 迭代代数为节点数3~5倍,或者采用某个估计函数Af(n) ,其中A为一个基准常数,f(n)为一个节点数的增函数. 交叉概率可设为Pc=0.9,变异概率为Pm=0.01.
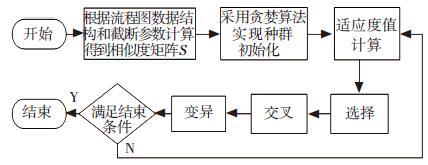
最终的算法运行流程如下:
|
图 3 遗传匹配算法流程图 |
根据前述工作,该节根据流程节点数不同,将流程库中的流程分成98类,即2~99个节点的流程根据其节点数各成一类. 每一类流程一般有8~12个. 通过对不同类别流程的匹配计算,观察算法的性能表现. 在语义相似度的计算上采用了基于《知网》的语义知识库及其词汇语义相似度计算方法,并结合前文的分析实现流程配对和相似度计算. 实验时,首先通过确定截断值对测试结果的影响来确定合适的实验参数;其次,在确定的截断值条件下,通过匹配的相似度结果和匹配过程的时间消耗来确定匹配综合效果.
定义相似度时间成本函数Ccosts,t:
| ${{C}_{\text{cost}}}\left( s,t \right)=\frac{At\left( 1-s \right)}{s-{{s}_{0}}+\alpha }+{{C}_{n}}.$ |
式中:t为所耗费的时间,A为比例调节常数,s为求解的相似度值,s0为通过贪婪算法得到的相似度值,α为一较小的常数,以避免分母为零;Cn为两流程节点数的减函数. 通过函数Cn的调节,使得在节点增多时,函数成本适当减小. Cn的确定与常数A和α相关,例如可取Cn=-Aeαn. 根据实验数据特点,也可采用以下变形:
| ${{C}_{\text{cost}}}\left( s,t \right)=\ln \left( \frac{At\left( 1-s \right)}{s-{{s}_{0}}+\alpha }+{{C}_{n}} \right).$ | (1) |
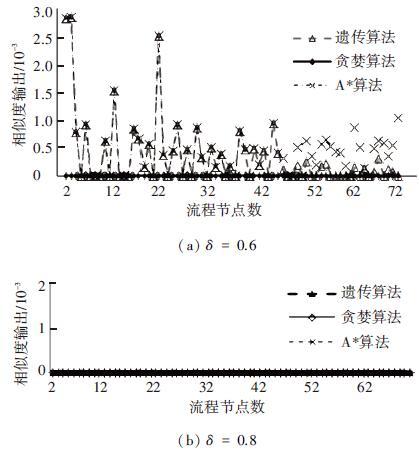
实验证明,截断值(δ)的选取对流程匹配算法的实用性具备重要影响,特别是A*算法在节点数逐渐增大约到15个节点时,平均耗时会开始超过1 s/百对. 增加至54个节点时,程序耗时已经超过2 d,因此采用文献[9]建议,δ的下界取0.6,此时得到的A*算法在相似度值和耗时两方面都处于可接受范围内. 实验中对贪婪算法、A*算法、遗传算法进行包括时间复杂度、匹配结果以及时间成本代价等指标的对比,截断参数δ可选0.6、0.8,当δ=0.6时,对比较果明显. 由于流程的相似度值差异值较小,为了清晰地表达实验结果,将3种算法得到的相似度值减去贪婪算法得到的值绘图,结果见图 4. 由图 4可知,与δ=0.6相比,δ 取0.8时,流程匹配相似度的绝对值整体下降了. 因为δ的变大,直接忽略相似度值较小的节点匹配,从而导致整体相似度值下降.
|
图 4 算法的匹配效果比较 |
从图 4可以清楚地看到3种算法得到的相似度值的差异. 由于贪婪算法自身减掉自身的值得到的值始终是0,因此,贪婪算法表现为一条恒为0的直线,延伸于坐标轴横轴方向上. 在δ为0.6时,可以看到遗传算法和A*算法大约在节点数达到45及其之前的匹配输出是完全重合的;当节点数>45时,遗传算法的值开始处于A*算法之下. 这说明遗传算法在节点数超过45时,不能再保证相似度值是最优解. 当δ为0.8时,遗传算法和A*算法得到的相似度值与贪婪算法相同,减掉贪婪算法的值后结果都为一条恒为0的直线,延伸于横轴方向上,如图 4(b)所示. 因此,δ超过0.8时,贪婪算法是最好的. 即当δ超过0.8时,截断值过于简化了算法. 然而如果实际需要,可以将δ设得比较大,如0.8. 但δ设得过大,可能使得匹配不到真正的最优解,从而导致匹配算法失去优势.
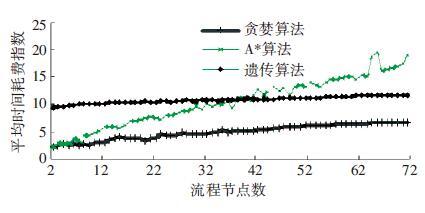
5 算法时间复杂度结果分析在测试了截断值对匹配结果的影响后,实验取δ=0.6对3种算法的时间复杂度进行测试. 图 5为3种算法随着节点数增加,时间复杂度的情况. 横轴表示节点数,纵轴表示每100对流程匹配所耗费的时间. 由于时间跨度较大,图中纵轴采用时间对数坐标.
|
图 5 算法平均时间复杂度随节点增多变化趋势 |
由图 5可知,贪婪算法在时间上表现最好. 同时,A*算法在起初节点数较少时,时间和贪婪算法相当. 当节点数>5时,A*算法时间复杂度急剧增长,并在节点数为37附近,超越遗传算法呈剧烈上升趋势. 在节点数为37处,A*算法的时间耗费约为11(e11ms约为12 s). A*算法的时间复杂度基本保持随着节点数逐渐增长而增长,偶尔出现时间耗费降低或者突然增大的情况,说明A*算法的波动性较大. 遗传算法的时间复杂度基本稳定,始终保持在11附近并缓慢增长. 出现以上实验现象是因为A*算法受启发策略的影响很大,同时其复杂度随着节点数的增加会呈现指数增长趋势,最终总体上体现出快速增长并偶有波动. 而采用贪婪算法,随着节点数的提升,时间复杂度呈对数增长模式,因此能有效避免状态空间爆炸问题. 遗传算法的复杂度取决于其迭代次数和进化过程,具备复杂度小且可控的特性.
6 时间成本评比基于式(1),参数采用了如下的取值:A=0.01,α=0.001,Cn=-Aeαn. 对实验数据进行二次处理,得出时间成本效果对比曲线.
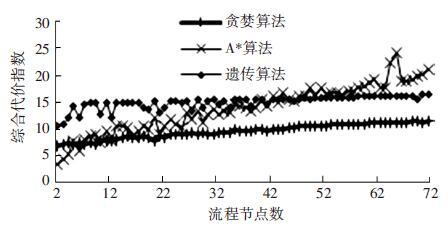
可以看到,图 6的趋势与图 5是一致的. 从图 6可得贪婪算法的成本基本上一直维持在最低. 因为贪婪算法的时间复杂度很小,使得贪婪算法在一些应用场景下始终具有优势. 遗传算法在节点数<37时,成本函数始终大于A*算法;超过37时,与A*算法相当,超过43个节点时,遗传算法相对于A*算法表现出优势,而且时间成本相对稳定,增长缓慢. 即当节点数超过43时,采用A*算法来求解匹配的最优值是不如遗传算法“划算”的. 综合前述实验结果,当流程节点达到一定数量时,采用遗传算法进行流程最优匹配是一个能兼顾匹配输出效果和时间成本的选择,对于实际应用来说,具备明显的折中优势.
|
图 6 相似度计算综合代价随节点增多的变化趋势对比 |
1) 从流程节点的语义相似度和流程结构匹配算法两方面进行了研究. 结合流程节点语义相似度和流程结构相似度的相关定义,导出了本文的流程相似度计算模型.
2) 针对流程相似度寻优过程,设计了一种基于遗传算法的过程寻优算法.
3) 对目标算法进行了实验验证,通过对实验数据的分析,证明了本文设计的流程匹配算法在匹配的时间复杂度和匹配输出方面的综合优化能力,对比已有的匹配过程寻优算法,本文算法体现出很好的实用价值.
鉴于时间和实验条件,本文虽然在流程匹配中尝试了对语义的考察,但还有进一步深入的空间,如实现本体语义的语义匹配,尝试其他新算法在匹配寻优过程中的应用等.
| [1] |
JIN T, WANG J, LA ROSA M, et al. Efficient querying of large process model repositories[J].
Computers in Industry,2013, 64 (1) : 41-49.
( 0) 0)
|
| [2] |
WANG P, LIU H. Assessing sentence similarity using wordnet based word similarity[J].
Journal of Software,2013, 8 (6) : 1451-1458.
( 0) 0)
|
| [3] |
LI H, TIAN Y, CAI Q. Improvement of semantic similarity algorithm based on WordNet[C]// 2011 6th IEEE Conference on Industrial Electronics and Applications (ICIEA). Beijing: IEEE, 2011:564-567.
( 0) 0)
|
| [4] |
郭永利, 卢颖颖. 基于Lucene对文件全文检索的研究与应用[J].
微型电脑应用,2014 (1) : 51-54.
( 0) 0)
|
| [5] |
李永春, 丁华福. Lucene的全文检索的研究与应用[J].
计算机技术与发展,2010, 20 (2) : 12-15.
( 0) 0)
|
| [6] |
付永贵. 一种改进的余弦向量度量法文本检索模型[J].
图书情报工作,2011 (19) : 115-119.
( 0) 0)
|
| [7] |
BERRETTI S, DELBIMBO A, VICARIO E. Efficient match-ing and indexing of graph models in content-based retrieval[J].
IEEE Transactions on Pattern Analysis and Machine Intelligence,2001, 23 (10) : 1089-1105.
( 0) 0)
|
| [8] |
COLOMOPALACIOS R, GOMEZBERBIS J M, GARCIAC-RESPO A, et al. SeMatching: using semantics to perform pair matching in mentoring processes[C]//2nd World Summit on the Knowledge Society. Chania: Springer Verlag, 2009:137-146.
( 0) 0)
|
| [9] |
DIJKMAN R, DUMAS M, GARCIABANUELOS L. Graph matching algorithms for business process model similarity search[C]//7th International Conference on Business Process Management. Ulm: Springer Verlag, 2009:48-63.
( 0) 0)
|
| [10] |
THANUJA M K, MALA C.
A search tool using genetic algorithm[M]. Chania: Springer, 2011 : 138 -143.
( 0) 0)
|
| [11] |
HONDA K, NAGATA Y, ONO I. A parallel genetic algorithm with edge assembly crossover for 100,000-city scale TSPs[C]// 2013 IEEE Congress on Evolutionary Computation (CEC). Cancun: IEEE,2013:1278-1285.
( 0) 0)
|
| [12] |
CEKMEZ U, OZSIGINAN M, SAHINGOZ O K. Adapting the GA approach to solve Traveling Salesman Problems on CUDA architecture[C]// 2013 IEEE 14th International Symposium on Computational Intelligence and Informatics (CINTI). Budapest: IEEE, 2013:423-428.
( 0) 0)
|
| [13] |
葛斌, 李芳芳, 郭丝路, 等. 基于知网的词汇语义相似度计算方法研究[J].
计算机应用研究,2010 (9) : 3329-3333.
( 0) 0)
|
| [14] |
周生宝, 郭俊芳. 本体映射中概念相似度计算的改进[J].
山西大同大学学报(自然科学版),2008 (4) : 38-40.
( 0) 0)
|
| [15] |
王婷. 本体相似度研究[J].
电脑知识与技术(学术交流),2007, 6 : 1609-1611.
( 0) 0)
|
| [16] |
张艳霞, 张英俊, 潘理虎, 等. 一种改进的概念语义相似度计算方法[J].
计算机工程,2012 (12) : 176-178.
( 0) 0)
|
| [17] |
胡哲, 郑诚. 改进的概念语义相似度计算[J].
计算机工程与设计,2010 (5) : 1121-1124.
( 0) 0)
|
| [18] |
DIJKMAN R, DUMAS M, DONGEN B V, et al. Similarity of business process models: Metrics and evaluation[J].
Information Systems,2011, 36 (2) : 498-516.
( 0) 0)
|
| [19] |
ZHU J, PUNG H K. Process matching: A structural approach for business process search[C]//Computation World: Future Computing, Service Computation, Adaptive, Content, Cognitive, Patterns, Computation World 2009. Athens: IEEE Computer Society, 2009:227-232.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


