2. 哈尔滨工业大学 能源科学与工程学院, 哈尔滨 150001
2. School of Energy Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
近年来,故障诊断技术得到了广泛深入地研究,对企业的关键机组实行状态监测和故障诊断,保障这些设备的安全高效运行,避免灾难性事故的发生,具有显著的经济效益和社会效益. 与传统的故障诊断技术不同,故障严重程度识别并不关注故障的类型,而是考虑在同一故障类型下的故障严重性信息,识别故障的严重程度可以帮助用户了解设备的运行状态及发展趋势,制定合理的维修计划,提高设备的利用率. 相比于故障检测和故障分类,故障严重程度识别更加困难,是故障诊断领域的一项特殊任务和新的挑战.
在故障严重程度识别中,按照不同的严重程度,可以将故障分为“轻微故障”,“中等故障”和“严重故障”. 不同严重程度之间存在序的关系,可以表示为:“严重故障”>“中等故障”>“轻微故障”,即“严重故障”表明设备的故障严重程度比“中等故障”和“轻微故障”高,“中等故障”比“轻微故障”的故障更严重. 进行故障严重程度识别时,要求工作人员人为地将故障划分为几个等级,例如可以将故障划分为“轻微故障”和“严重故障”,当发现设备是“轻微故障”时,表明已出现异常,需要立刻查找原因安排维修;当发现是“严重故障”时,为避免恶性事故的发生,必须马上停机. 这种按照故障的严重程度进行分类的问题可以理解为模式识别和机器学习中的有序分类问题(也称为排序问题或有序回归问题)[1-3]. 进行故障严重程度识别的关键问题是如何利用和表达数据中潜在的有序信息,而不是简单的将其看作是一般分类问题进行分类学习.
目前,故障严重程度识别主要是建立分类学习模型,实现不同严重程度信息的自动识别. 2009年,曾庆虎等[4]采用核主成分分析(KPCA)方法进行多通道信息融合,建立基于隐半马尔可夫模型(HSMM)的故障预测模型实现设备退化状态识别. Lei等[5]人为地将齿轮破坏,并分成几种不同程度的裂纹,在不同转速和负载下收集振动数据,设计了基于加权欧式距离的K近邻分类算法(WKNN)进行齿轮裂纹程度识别. Li等[6]利用流行学习算法提取故障的非线性特征,并应用经验模态分解方法进行齿轮裂纹程度识别. Cheng等[7]利用统计方法进行特征选择,提出了基于灰色关联度分析的故障程度识别方法. Zhao等[8]提出了基于相关系数的有序分类特征选择算法,并进行实验分析,指出了分析故障严重程度识别问题时有序分类学习算法比一般分类算法更有效. Wu等[9]采用基尼系数度量不同故障的严重性,研究了基于故障注入技术的严重程度信息识别方法. Jiang等[10]提出了基于统计参数(均值)和残差信号的故障严重性识别方法.
故障特征空间可能含有成百上千个特征,这些特征中只有很少一部分是与故障严重程度相关的,并且部分故障特征和严重程度之间存在单调变化趋势:即随着故障的严重程度的增加特征值增大或减小,这类特征被称为是单调的故障特征. 对应的,与故障严重程度不存在单调依赖关系的特征则称为非单调故障特征. 单调故障特征能够反映出与不同严重程度之间的单调依赖关系,能够直观地区分故障的不同严重程度信息. 对于这种非单调特征和单调特征混合存在的情况,需要设计混合的有序分类特征选择算法.
本文首先提出非单调特征和单调特征混合的有序分类特征选择算法,然后将提出的特征选择算法应用于齿轮裂纹程度识别,构建基于有序分类的故障严重程度识别模型.
1 有序分类定义1 给定决策系统 DT=〈U,A,D〉, 其中 U={x1,x2,…,xN} 表示有限非空样本集, A={a1,a2,…,aJ} 是特征集, D={d1,d2,…,dK} 是决策类别集. 如果不同的决策类别之间存在序的关系,可以假设 d1<d2<…<dK, 则称此决策系统为有序分类决策系统.
样本 xi∈U 在特征 a∈A 和决策 D 上的取值分别记为 v(xi,a) 和 v(xi,D), 特征与决策集上的序关系记为“ ≥ ”和“ ≤”. 令 v(xi,a)≥v(xj,a) 和 v(xi,D)≥v(xj,D) 分别表示在特征 a 和决策 D 上样本 xj 不好于 xi. 同理, xi 不好于 xj 记作 xi≤axj 和 xi≤Dxj.
定义2 给定有序决策系统 DT=〈U,A,D〉, 对 ∀xi∈U,a∈A,xi 关于特征 a
| $\begin{align} & {{[{{x}_{i}}]}^{\le }}_{a}=\{{{x}_{j}}\in U{{x}_{j}}{{\le }_{a}}{{x}_{i}}\}; \\ & {{[{{x}_{i}}]}^{\ge }}_{a}=\{{{x}_{j}}\in U{{x}_{j}}{{\ge }_{a}}{{x}_{i}}\}. \\ \end{align}$ |
相应的,对 B⊆A,xi 关于 B 和 D 的有序信息粒子分别定义为
| $\begin{align} & {{[{{x}_{i}}]}^{\le }}_{B}=\{{{x}_{j}}\in U{{x}_{j}}{{\le }_{B}}{{x}_{i}}\}; \\ & {{[{{x}_{i}}]}^{\ge }}_{B}=\{{{x}_{j}}\in U{{x}_{j}}{{\ge }_{B}}{{x}_{i}}\}; \\ & {{[{{x}_{i}}]}^{\le }}_{D}=\{{{x}_{j}}\in UD({{x}_{j}})\le D({{x}_{i}})\}; \\ & {{[{{x}_{i}}]}^{\ge }}_{D}=\{{{x}_{j}}\in UD({{x}_{j}})\ge D({{x}_{i}})\}. \\ \end{align}$ |
式中:若 ∀a∈B, 都有 xj≤axi, 则称 xj≤Bxi.
定义3 给定有序决策系统 DT=〈U,A,D〉, 单调约束条件指的是:对 ∀xi,xj∈U, 如果 xi≤Bxj, 有 D(xi)≤BD(xj) (或者 xi≥Bxj⇒D(xi)≥BD(xj)).
特征与决策之间的单调约束关系是指:假定样本 xi 在特征集 B 上取值比样本 xj 大,那么 xi 的决策也会比 xj 的决策好,否则就违反了单调一致性.
事实上,单调分类是一类特殊的有序分类问题,即它不仅强调决策类别之间存在序结构,而且假设全部特征与决策之间存在单调约束关系. 但单调约束关系是一个很强的限制条件,绝大多数现实的有序决策任务往往不能满足全部特征都与决策之间具有单调依赖关系,可能只有部分特征为单调特征,大部分特征是非单调特征.
针对单调特征和非单调特征混合存在的情况,本文研究有序分类的特征选择问题. 首先要解决的问题是对于给定的有序数据集,如何判断哪些特征是单调特征,哪些特征是非单调特征.
2 特征单调性评定方法首先给出排序互信息的定义,具体信息可参考文献[11].
定义4 给定有序决策系统DT=<U,A,D>,B⊆A,C⊆A. B和C在U上的前向互信息定义为
| $RM{{I}^{\le }}\left( B,C \right)=-\frac{1}{n}\sum\limits_{i=1}^{n}{\log \frac{\left| |{{x}_{i}}{{]}^{\le }}_{B}\left| \times \right|{{[{{x}_{i}}]}^{\le }}_{C} \right|}{\left| n\times {{[{{x}_{i}}]}^{\le }}_{B}\cap {{[{{x}_{i}}]}^{\le }}_{C} \right|}};$ |
后向互信息定义为
| $RM{{I}^{\ge }}\left( B,C \right)=-\frac{1}{n}\sum\limits_{i=1}^{n}{\log \frac{\left| |{{x}_{i}}{{]}^{\ge }}_{B}\left| \times \right|{{[{{x}_{i}}]}^{\ge }}_{C} \right|}{\left| n\times {{[{{x}_{i}}]}^{\ge }}_{B}\cap {{[{{x}_{i}}]}^{\ge }}_{C} \right|}}.$ |
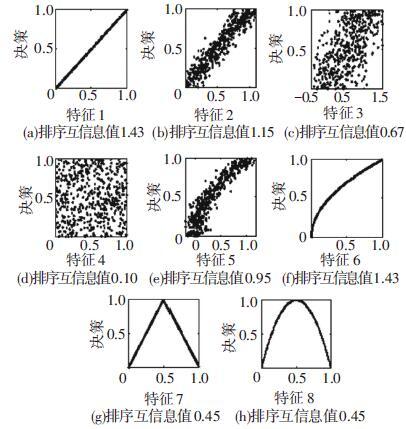
下面举列说明排序互信息可以表征特征与决策之间的单调一致性程度. 图 1展示了8个特征(样本数500)的散点图,并计算了每个特征与决策之间的排序互信息值(这里只考虑前向排序互信息,后向排序互信息可以得到类似的结论).
|
图 1 各特征的散点图分布及其与决策的排序互信息值 |
第1个特征与决策之间具有线性的单调一致关系,在第1个特征的基础上加入了不同噪声水平的噪声得到了第2、3个特征. 相比特征1,特征2和3与决策之间的单调一致性程度降低,相应的排序互信息值也随之减小,从1.43分别降为1.15和0.67. 第4个特征完全是杂乱的,与决策之间不存在单调性,此时得到的排序互信息值很小,几乎接近于0. 第6个特征与决策之间满足非线性的单调一致关系,特征值随着决策值的增大单调增加. 虽然特征6随着决策非线性单调变化,但是特征6得到的排序互信息与特征1相同,表明排序互信息可以反映特征与决策之间的单调相关性,不管这种单调关系是线性的还是非线性的. 第5个特征是在第6特征的基础上加入了噪声,排序互信息值从1.43降为0.95. 第7、8 这两个特征的值先是单调增加然后再减少,相应的排序互信息值低于其它特征(除了特征4). 通过以上的对比分析发现,特征与决策的单调一致性程度可通过排序互信息表达. 特征与决策之间的单调一致性程度越高,对应排序互信息的值越大;反之单调一致性程度就越小. 因此,可以采用排序互信息作为评价指标来区分原始特征集中哪些特征是单调特征,哪些是非单调特征.
在实际的有序学习任务中,需要假定一个阈值,将原始的特征集合分成两个特征子集:非单调特征子集和单调特征子集. 如果某特征与决策的排序互信息>预设的阈值,将此特征判为单调特征,否则就是非单调特征. 在没有任何先验知识的情况下,本文将所有特征按照排序互信息值大小排序,将原始特征集合分为两部分,单调特征和非单调特征的数量相同.
3 基于混合单调特征的有序分类特征选择算法特征选择算法包含两个主要步骤:特征评价函数和最优子集搜索策略. 首先针对有序分类中非单调特征和单调特征混合存在的情况,定义有序分类的分类一致性假设条件,将其作为特征评价函数评价一个混合单调的特征子集与决策之间的相关性,然后采用遗传算法(GA)作为搜索策略构造有序分类的特征选择算法.
3.1 非单调特征和单调特征混合的有序分类一致性定义5 给定有序决策系统 DT=<U,A,D>, 若特征集合 A 中只有部分特征与决策之间满足单调依赖关系,既包含与决策之间满足单调依赖关系的单调特征,又包含非单调特征,则称此有序决策系统为混合单调特征的有序决策系统.
定义6 给定单调特征和非单调特征混合的有序决策系统 DT=<U,A,D>,∀B⊆A,∀xi,xj∈U, 如果:
1) 样本 xi 和 xj关于B中的非单调的符号特征满足等价关系,且数值特征满足相似关系;
2) 关于B中的单调特征,样本xi优于xj;则称在混合单调特征集合 B,xi 优于 xj ,记为 xi≥Bxj.
对非单调特征和单调特征混合存在的有序分类任务,定义混合单调特征的有序分类的分类一致性假设.
定义7 对混合单调特征集合 B⊆A,∀xi,xj∈U,若xi≥Bxj,有D(xi)≥D(xj),则称D关于B是混合单调分类一致的,否则违背了混合单调特征的有序分类的分类一致性.
∀B⊆A,B的混合单调分类一致性越大,表征B对决策D的分类能力越强,可以将其作为特征评价函数度量特征子集的质量.
3.2 遗传算法遗传算法(genetic algorithm,简称GA)[12-13]的基本框架包括参数编码、初始种群选取、适应度函数和遗传操作等4部分. GA基于生物进化的适者生存理论,模拟遗传学的生物遗产进化的过程,并以适应度函数评价种群中的个体优劣程度,即以适应度来表征种群中的个体对环境生存能力的强弱. 在实际应用中,适应度函数的设计需要根据所求解问题本身的要求而定. 设定了适应度函数后,遗传操作通过模拟生物基因遗传原理,根据个体对环境的适应度,进行选择、交叉、变异等遗传操作,从而实现优胜劣汰的进化过程. 经过多次迭代后,从最后一代种群中选出适应度函数值最大的个体,进而得到所求问题的最优解.
本文采用二进制编码,对于任意的特征子集 B⊆A,将B的混合单调分类一致性作为适应度函数, 进而度量GA算法每次选择出来的特征子集 B 的适应度,而算法最终输出的最大的混合单调分类一致性(即适应度)对应的特征子集即为最终的最优子集.
GA算法采用轮盘赌选择算子以及单点交叉方式,交叉率设为0.8,变异率是0.01.
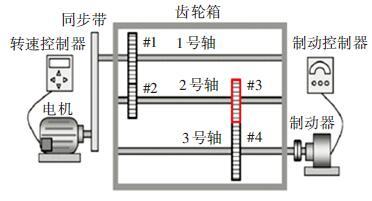
4 基于有序分类的齿轮裂纹程度识别 4.1 实验描述和数据获取本文采用的实验系统结构如图 2所示. 系统构成中包括1个齿轮箱,提供负载的磁力制动器和用以驱动齿轮箱旋转的三相交流电机[5].
|
图 2 实验系统图 |
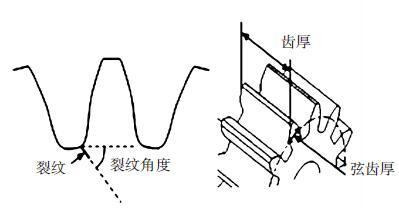
在齿轮箱中,齿轮#1和齿轮#2啮合,齿轮#3和齿轮#4啮合,齿轮#3为测试齿轮. 在齿轮箱外壳上安装两个传感器收集齿轮箱的 x(水平)和y(垂直)两个方向的振动数据. 人为地将测试齿轮破坏成不同的裂纹深度和宽度,得到不同故障严重程度的齿轮. 齿轮的裂纹程度信息见图 3,裂纹角度为 α,a为弦齿厚度的一半,齿厚为b. 共采用了3个不同裂纹程度的齿轮, 详细信息见表 1,其中F0表示正常完好的齿轮,F1和F2分别代表两个不同裂纹程度的测试齿轮.
|
图 3 齿轮的裂纹程度信息 |
| 表 1 裂纹的几何形状 |
在3种负载(load0,load1,load2),4种转速(1 200,1 400,1 600,1 800 r/min)以及3种不同裂纹程度(F0,F1,F2)情况下,共收集到36个故障样本. 重复实验3次,整理得到的齿轮裂纹程度识别数据集共含有108个样本.
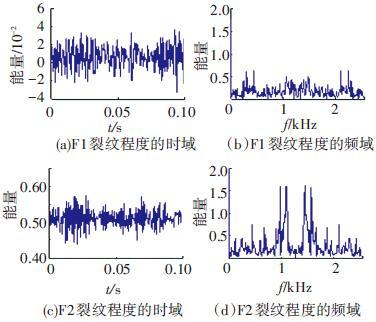
图 4是在不同的裂纹程度(F1和F2)下,测试齿轮在时域和频域中的数据,由图 4可见,在不同的故障严重程度时,时域和频域的信息差异很大,可从中抽取特征对其进行评判.
|
图 4 故障特征的时域和频域 |
对振动数据提取特征,特征集中包括时域特征、频域特征以及特别为齿轮故障识别设计的特征[5],具体的特征信息见表 2. 构建的故障严重程度识别数据集有108个样本,52个特征.
| 表 2 特征编号和对应的特征说明[14] |
为有效识别齿轮裂纹的程度,本文在故障严重程度识别数据集的原始特征空间中,采用前述的特征选择算法,以去除无关和冗余的特征,得到与故障严重程度相关的最优特征子空间,并经实验分析此特征子空间的有效性.
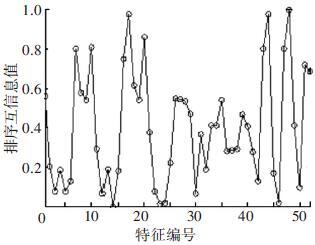
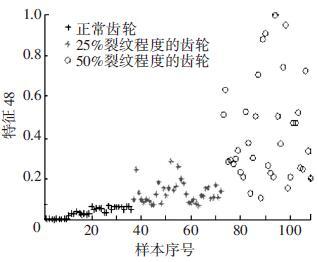
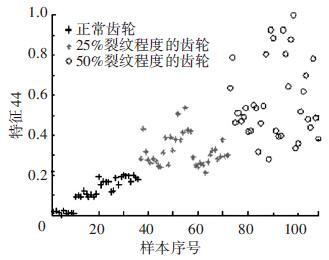
实验处理中,首先计算特征与故障严重程度之间的排序互信息,如图 5所示. 由图 5可以看出,特征48和特征44的排序互信息相对较大,说明它们与决策之间的具有较强的单调相关性. 图 6为特征48与不同裂纹严重程度之间的关系,其中‘+’表示正常齿轮,‘*’表示25%裂纹程度的齿轮,‘o’表示50%裂纹程度的齿轮. 如图 6可知,特征48能够清晰地将不同的故障严重程度信息区分开,并能有效地反映故障严重程度的单调变化趋势. 故障特征值增大,可发现故障严重程度随之增加(故障严重程度高). 由图 6可知,当特征48的特征值超过0.07时,表示齿轮发生了故障. 图 7为特征44与不同裂纹严重程度之间的关系. 在特征44上同样可以看出故障程度的发展进程,当样本在特征44上的值超过0.2时,表示齿轮发生了故障.
|
图 5 故障特征的排序互信息 |
|
图 6 特征48和裂纹程度之间的关系 |
|
图 7 特征44和裂纹程度之间的关系 |
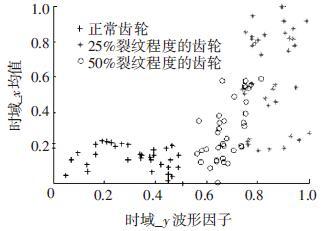
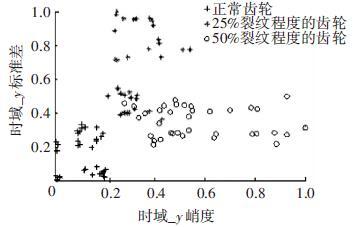
应用提出的特征选择算法进行特征选择,得到最优特征子集共包含7个特征,特征编号分别为:2、13、15、17、28、44和48. 在此特征子集中,非单调特征包括2、13和15,单调特征为17、28、44和48等. 随机取3组特征两两组合,图 8~10展示了二维特征空间的数据散点图. 可以看出,不同严重程度(不同颜色)的故障样本在这些特征的空间上重叠区域很小,即便用最简单的基于直线的区间划分方法也可将不同严重程度的样本分开,可见这些特征可以清晰地将不同的故障程度信息区分开. 而且特征48和44也能够反映出故障严重程度的单调变化趋势. 图 9是特征2和特征15组合形成的特征子集在二维图上的散点分布,这个包含2个特征的子集合对故障严重程度有良好的区分能力.

|
图 8 特征48和特征44的散点图 |
|
图 9 特征2和特征15的散点图 |
|
图 10 特征13和特征17的散点图 |
特征选择后,应用分类算法进行故障严重程度识别. 共选取了6个分类算法: OSDL、OLM、RMDT、RANK TREE、CART和KNN,其中CART和KNN是一般分类学习算法,OSDL、OLM、RMDT和RANK TREE是专门为有序分类设计的学习算法[15-17]. 将数据集分成10份,各算法分别在10次不同的训练集上建模,并在对应的测试集上测试,对所有10次实验的结果求均值,计算特征选择后得到的特征子集的分类性能. 表 3和表 4分别给出了6个分类学习算法的故障严重程度的平均识别结果. 表的第二列表示的分别是采用原始数据的分类错误率和平均分类损失,最后一行为各算法的平均计算结果,其中平均分类损失定义为:$\frac{1}{N}\sum\limits_{n=1}^{N}{\left| {{y}_{n}}-{{{{y}'}}_{n}} \right|}$(假定数据集的样本总数为 N,yn 为样本的实际类别, yn′ 为预测的类别).
| 表 3 原始特征集和特征子集的分类错误率比较 |
| 表 4 选中的特征子集和原始特征集的平均分类损失比较 |
从表 3、4可以看出,相比原始数据,特征选择后再进行分类得到的平均分类错误率由15.36%降低为5.25%,平均分类损失从11.36%降低为4.41%. 实验分析结果表明: 本文提出的特征选择算法明显地减少了特征空间的维数,降低了故障严重程度识别的错误率和平均分类损失.
5 结论1) 本文设计了有序分类的特征选择算法,并将其应用于齿轮裂纹程度识别中以提高故障严重程度识别的准确性.
2) 针对非单调特征和单调特征混合存在的情况,定义了有序分类一致性假设条件,并将其作为特征评价函数. 与遗传算法相结合得到原始特征集合中的最优的特征子集,并将提出的有序分类特征选择算法应用到齿轮裂纹程度识别,构建了基于混合单调特征的有序分类故障严重程度识别模型.
3) 实验结果表明,提出的特征选择算法既降低了特征空间的维数,又提高了故障严重程度识别的准确性.
| [1] |
FRANK E, HALL M. A simple approach to ordinal classification[C]// Proc Europ Conf on Machine Learning. Beilin: Springer, 2001: 145-156.
( 0) 0)
|
| [2] |
KOTLOWSKI W, DEMBCZYNSKI K, GRECO S, et al. Stochastic dominance-based rough set model for ordinal classification[J].
Information Sciences,2008, 178 (21) : 4019-4037.
( 0) 0)
|
| [3] |
BLASZCZYNSKI J, SLOWINSKI R, SZELAG M. Probabilistic rough set approaches to ordinal classification with monotonicity constraints[J].
Computational Intelligence for Knowledge-Based Systems Design,2010, 6178 : 99-108.
( 0) 0)
|
| [4] |
曾庆虎, 邱静, 刘冠军. 基于小波相关特征尺度熵的HSMM设备退化状态识别与故障预测方法[J].
仪器仪表学报,2009, 29 (12) : 2559-2564.
( 0) 0)
|
| [5] |
LEI Yaguo, ZUO M J. Gear crack level identification based on weighted K nearest neighbor classification algorithm[J].
Mechanical Systems and Signal Processing,2009, 23 (5) : 1535-1547.
( 0) 0)
|
| [6] |
LI Zhixiong, YAN Xinping, JIANG Yu, et al. A new data mining approach for gear crack level identification based on manifold learning[J].
Mechanics,2012, 18 (1) : 29-34.
( 0) 0)
|
| [7] |
CHENG Zhe, HU Niaoqing, ZHANG Xiaofei. Crack level estimation approach for planetary gearbox based on simulation signal and GRA[J].
Journal of Sound and Vibration,2012, 331 (26) : 5853-5863.
( 0) 0)
|
| [8] |
ZHAO Xiaomin, ZUO M J, LIU Zhiliang, et al. Diagnosis of artificially created surface damage levels of planet gear teeth using ordinal ranking[J].
Measurement,2013, 45 (1) : 132-144.
( 0) 0)
|
| [9] |
WU Jianing, YAN Shaoze. Fault severity evaluation and improvement design for mechanical systems using the fault injection technique and gini concordance measure[J].
Mathematical Problems in Engineering,2014, 2014 (1) : 759-765.
( 0) 0)
|
| [10] |
JIANG Fan, LI Wei, WANG Zhongqiu, et al. Fault severity estimation of rotating machinery based on residual signals[J].
Advances in Mechanical Engineering,2015, 15 (11) : 1067-1077.
( 0) 0)
|
| [11] |
HU Qinghua, GUO Maozu, YU Daren, et al. Information entropy for ordinal classification[J].
Science China Information Sciences,2010, 53 (6) : 1188-1200.
( 0) 0)
|
| [12] |
HOLLAND J H.
Adaptation in natural and artificial systems[M]. Ann Arbor: University of Michigan Press, 1975 .
( 0) 0)
|
| [13] |
YANG J, HONAVAR V. Feature subset selection using a genetic algorithm[J].
IEEE Trans Intelligent Systems and Their Applications,1998, 13 (2) : 44-49.
( 0) 0)
|
| [14] |
潘巍巍. 故障严重程度识别的有序分类特征分析方法[D]. 哈尔滨: 哈尔滨工业大学, 2013.
( 0) 0)
|
| [15] |
XIA Fen, ZHANG Wensheng, LI Fuxin, et al. Ranking with decision tree[J].
Knowledge and Information Systems,2008, 17 (3) : 381-395.
( 0) 0)
|
| [16] |
HU Qinghua, CHE Xunjian, ZANG Lei, et al. Rank entropy based decision trees for monotonic classification[J].
IEEE Transactions on Knowledge and Data Engineering,2012, 24 (11) : 2052-2064.
( 0) 0)
|
| [17] |
BEN-DAVID A, STERLING L, TRAN T D. Adding monotonicity to learning algorithms may impair their accuracy[J].
Expert Systems with Applications,2009, 36 (3) : 6627-6634.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


