2. 西安交通大学 高端制造装备协同创新中心, 西安 710054
2. Collaborative Innovation Center of High-End Manufacturing Equipment, Xi’an Jiaotong University, Xi’an 710054, China
准双曲面齿轮被广泛用作汽车主减速器齿轮,由于小、大轮之间偏置距的存在,可有效增加汽车的平稳性或者越野性,因此,对准双曲面齿轮进行研究更具有普遍意义.
国内外一些学者对对准双曲面齿轮的设计、制造和加工进行了研究[1-5].Kawasaki等[6]分别采用解析和实验方法研究了大型摆线齿螺旋锥齿轮的齿面接触模式.Park等[7]提出了一种准双曲面齿轮表面磨损的近似计算方法.Mohammadpour等[8]对不同准双曲面齿轮在大负荷下的非牛顿混合弹流动力学进行了分析.Takeda等[9]对准双曲面齿轮的啮合性能进行了分析,并通过实验测量了传动误差.Simon[10]针对面滚式准双曲面齿轮提出了一种优化方法,用来系统地定义刀盘参数和机床加工参数.
准双曲面齿轮的啮合质量需要通过正确的切齿参数的调整来实现.基于局部综合法[11-12]的切齿设计可以满足以上要求.杨宏斌等[13]研究了基于局部综合法的刀倾半展成(HFT)法加工高齿准双曲面齿轮的切齿参数设计,从文献中可以看出,该方法很难控制接触迹线为直线,导致齿轮副对安装误差的敏感性较大.刀倾全展成(HGT)方法,大轮采用双面刀盘展成加工,虽然加工效率没有成形法高,但是齿面曲率特性好,能更好地控制齿轮的啮合性能,因此,本文对HGT准双曲面齿轮进行研究.方宗德等[14]通过局部综合法对HGT准双曲面齿轮的优化切齿设计进行了前期理论探索,并没有通过算例给以定量计算和验证.本文作者曾对HGT准双曲面齿轮进行了工作齿面的理论推导,并进行了TCA计算[15],然而该工作无法对齿轮的啮合性能进行预控.
综上所述,在已有螺旋锥齿轮主动设计技术中,没有将齿面的高性能设计与加工结合起来.本文结合展成法和刀倾法,提出基于局部综合法对HGT准双曲面齿轮进行加工参数设计研究,实现对齿面的主动设计,并通过TCA定量分析验证了参数推导的正确性.
1 局部综合法基本原理简介局部综合法[1]是一种用于研究齿轮啮合的有效方法,基本思想是:根据大轮刀具参数和轮坯参数确定大轮的切齿参数,在大轮齿面上选取一参考点M(即一阶接触参数,参考点的位置决定了啮合区的位置),计算出参考点处大轮齿面的主曲率和主方向,并预置参考点处的3个二阶接触参数(即传动比函数的一阶导数m′21 、大轮齿面上接触迹线和齿根的夹角η2以及接触椭圆的长半轴长度a),这些参数决定了传动误差曲线的形状与幅值、接触迹线方向和啮合区的宽度;然后,求出参考点处小轮的主曲率和主方向,在此基础上确定小轮的切齿参数.
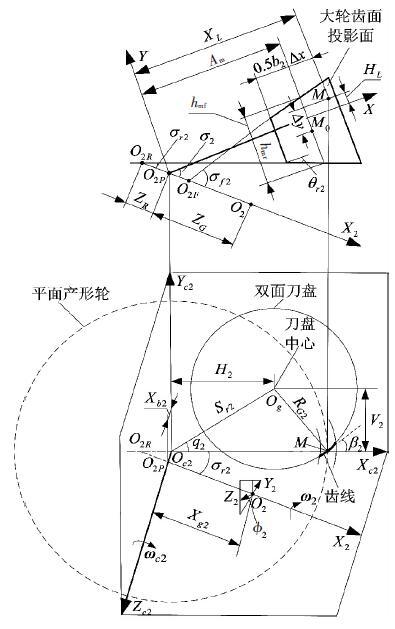
2 大轮加工参数及参考点的确定 2.1 确定大轮加工参数大轮切齿参数设计坐标系如图 1所示.图 1中,O2F、O2P、O2和O2R分别为面锥顶点、节锥顶点、交叉点和根锥顶点,b2为大轮齿宽,Am为大轮中点锥距,ZG和ZR分别为节锥顶点到设计交叉点的距离和节锥顶点到根锥顶点的距离,H2和V2分别为大轮刀盘的水平刀位和垂直刀位,Sr2和q2分别为径向刀位和角向刀位,RG2为刀盘半径,β2为大轮中点螺旋角.Oc2是大轮机床中心,也是平面产形轮的中心,Og是刀盘中心.σ2、σr2和θr2分别为大轮的节锥角、根锥角和齿根角.X2为大轮的旋转轴,坐标系O2-X2Y2Z2为大轮加工坐标系,φ2为大轮加工转角;X与大轮节锥线重合,坐标系O2p-XY为大轮旋转投影面坐标系.
|
图 1 大轮切齿参数设计坐标系 |
给定垂直轮位Em2=0,根据图 1,大轮加工参数为
| $\begin{align} & {{H}_{2}}=({{A}_{m}}+\Delta x)\text{cos}~{{\theta }_{r2}}-{{R}_{G2}}\text{sin }\!\!~\!\!\text{ }{{\beta }_{2}}, \\ & {{V}_{2}}={{R}_{G2}}\text{cos}~{{\beta }_{2}}, \\ & {{S}_{r2}}=\sqrt{{{H}_{2}}+{{V}_{2}}}, \\ & {{q}_{2}}=\text{si}{{\text{n}}^{-1}}({{V}_{2}}/{{S}_{r2}}), \\ & {{X}_{G2}}=-{{Z}_{G}}, \\ & {{X}_{B2}}={{Z}_{R}}sin~{{\sigma }_{r2}}, \\ & {{C}_{r2}}=cos~{{\theta }_{r2}}/sin~{{\sigma }_{2}}. \\ \end{align}$ |
式中:Xg2、Xb2和Cr2分别是轴向轮位、床位和滚比.至此,大轮的加工参数已完全确定.
2.2 确定参考点如图 1中所示,hmf和hmr分别是大轮中点齿顶高和中点齿根高,所以,中点全齿高
| ${{h}_{{}}}m={{h}_{mf}}+{{h}_{mr}};$ |
M0是齿面中点,
| $$ |
M是要确定的参考点,Δx和Δy分别是M点在齿宽和齿高方向距齿面中点M0的距离,M点的位置由参数XL和HL决定:
| $({{X}_{{{M}_{0}}}}={{A}_{{}}}m,{{Y}_{{{M}_{0}}}}={{h}_{mf}}-{{h}_{m}}/2或{{Y}_{{{M}_{0}}}}={{h}_{{}}}m/2-{{h}_{mr}})$ |
因此,调整Δx和Δy的值,即可按需要确定参考点M的位置,同时,根据XL和HL,可计算出M点处的大轮刀盘转角、摇台转角和刀盘锥面参数.
2.3 参考点大轮的主方向和主曲率根据文献[1]中线接触计算公式,由大轮刀盘切削面的主曲率和主方向,求出大轮齿面上参考点的主曲率和主方向.
大轮刀盘切削锥面图见文献[15]中图 1(a)所示.其位矢和单位法矢如下:
| $\begin{align} & {{r}_{g}}=\left[ \begin{matrix} ({{r}_{c2}}-{{S}_{g}}\text{sin}~{{\alpha }_{2}})\text{cos}~{{\theta }_{g}} \\ ({{r}_{c2}}-{{S}_{g}}\text{sin}~{{\alpha }_{2}})\text{sin}~{{\theta }_{g}} \\ -{{S}_{g}}\text{cos}~{{\alpha }_{2}} \\ 1 \\ \end{matrix} \right], \\ & {{n}_{g}}=\left[ \begin{matrix} -\text{cos}~{{\alpha }_{2}}\text{cos}~{{\theta }_{g}} \\ -\text{cos}~{{\alpha }_{2}}\text{sin}~{{\theta }_{g}} \\ \text{sin}~{{\alpha }_{2}} \\ \end{matrix} \right]. \\ \end{align}$ |
式中: rc2、Sg、α2和θg分别表示大轮内刀刀尖半径、刀盘锥面参数、刀盘齿形角和刀盘转角.
所以,大轮刀盘切削锥面的主方向表示为
| $e_{s}^{\left( g \right)}=\left( \frac{\partial {{r}_{g}}}{\partial {{\theta }_{g}}} \right)/\left( \left| \frac{\partial {{r}_{g}}}{\partial {{\theta }_{g}}} \right| \right)=\left[ \begin{matrix} -\sin {{\theta }_{g}} \\ \cos {{\theta }_{g}} \\ 0 \\ \end{matrix} \right],$ | (1) |
| $e_{q}^{\left( g \right)}=\left( \frac{\partial {{r}_{g}}}{\partial {{S}_{g}}} \right)/\left( \left| \frac{\partial {{r}_{g}}}{\partial {{S}_{g}}} \right| \right)=\left[ \begin{matrix} -\sin {{\alpha }_{2}}\cos {{\theta }_{g}} \\ -\sin {{\alpha }_{2}}\sin {{\theta }_{g}} \\ -\cos {{\alpha }_{2}} \\ \end{matrix} \right].$ | (2) |
相应的大轮刀盘切削锥面的主曲率表示为
| $k_{s}^{(g)}=\text{cos}~{{\alpha }_{2}}({{r}_{c2}}-{{S}_{g}}\text{sin}~{{\alpha }_{2}}),k_{q}^{(g)}=0.$ | (3) |
啮合坐标系见文献[15]中图 3所示.在参考点M,齿轮副的瞬时传动比等于理论值(两齿轮的齿数比),因此大轮和小轮在参考点的啮合转角ψ2(M) 可通过啮合方程求出.将式(1)~(3)经过坐标变换到机床坐标系:
| $\left\{ \begin{align} & {{r}_{c2}}={{M}_{c2g}}{{r}_{g}}, \\ & {{n}_{c2}}={{L}_{c2g}}{{n}_{g}}. \\ \end{align} \right.$ | (4) |
| $\left\{ \begin{align} & e_{sc2}^{\left( g \right)}={{L}_{c2g}}e_{s}^{\left( g \right)}, \\ & e_{qc2}^{\left( g \right)}={{L}_{c2g}}e_{q}^{\left( g \right)}, \\ & k_{sc2}^{\left( g \right)}=k_{s}^{\left( g \right)}, \\ & k_{qc2}^{\left( g \right)}=k_{q}^{\left( g \right)}. \\ \end{align} \right.$ | (5) |
式中:rc2、nc2分别为机床坐标系中大轮齿面参考点M处的位矢和法矢;Mc2g为刀盘坐标系到机床坐标系的转换矩阵;Lc2g为Mc2g的旋转矩阵.Mc2g可表示如下:
| $\begin{align} & {{M}_{c2g}}=\left[ \begin{matrix} \cos {{\gamma }_{2}}\cos {{\phi }_{g}} & \cos ~{{\gamma }_{2}}\sin ~{{\phi }_{g}} & \sin {{\gamma }_{2}} & \cos ~{{\gamma }_{2}}({{H}_{2}}\cos ~{{\phi }_{g}}+{{V}_{2}}\sin ~{{\phi }_{g}})-{{X}_{b2}}\sin ~{{\gamma }_{2}} \\ -\sin {{\phi }_{g}} & \cos {{\phi }_{g}} & 0 & -{{H}_{2}}\sin {{\phi }_{g}}+{{V}_{2}}\cos {{\phi }_{g}} \\ -\sin ~{{\gamma }_{2}}\cos {{\phi }_{g}} & -\sin ~{{\gamma }_{2}}\sin {{\phi }_{g}} & \cos ~{{\gamma }_{2}} & -\sin ~{{\gamma }_{2}}({{H}_{2}}\cos {{\phi }_{g}}+{{V}_{2}}\sin {{\phi }_{g}})-{{X}_{b2}}\cos ~{{\gamma }_{2}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right]. \\ & ~ \\ \end{align}$ |
将式(5)代入文献[1]中线接触公式,可得机床坐标系中大轮齿面参考点M处的主方向efc2(2)和ehc2(2),以及主曲率kfc2(2) 和khc2(2),其中,上标“2”表示大轮齿面Σ2的主方向和主曲率.
同理,将式(4)和(5)变换到大轮坐标系中,可得到大轮齿面参考点M处的位矢r2、法矢n2、主方向ef(2) 、eh(2) 和主曲率kf(2) 、kh(2):
| $\begin{matrix} {{r}_{2}}={{M}_{2c2}}{{r}_{c2}}, & {{n}_{2}}={{L}_{2c2}}{{n}_{c2}}, \\ e_{f}^{\left( 2 \right)}={{L}_{2c2}}e_{sc2}^{\left( g \right)}, & e_{h}^{\left( 2 \right)}={{L}_{2c2}}e_{qc2}^{\left( g \right)}, \\ k_{f}^{\left( 2 \right)}=k_{sc2}^{\left( g \right)}, & k_{h}^{\left( 2 \right)}=k_{qc2}^{\left( g \right)}. \\ \end{matrix}$ |
式中: M2c2为机床坐标系到大轮坐标系的转换矩阵,L2c2为M2c2的旋转矩阵.M2c2可表示如下:
| ${{M}_{2/2}}=\left[ \begin{matrix} 1 & 0 & 0 & {{X}_{g2}} \\ 0 & \cos {{\phi }_{2}} & -\sin {{\phi }_{2}} & 0 \\ 0 & \sin {{\phi }_{2}} & \cos {{\varphi }_{2}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right].$ |
然后,再变换到啮合坐标系,得到啮合坐标系中大轮齿面参考点处的位矢rh(2) 、法矢nh(2) 、主方向eⅠ(2) 、eⅡ(2) 和主曲率kⅠ(2)、kⅡ(2):
| $\left\{ \begin{align} & r_{h}^{\left( 2 \right)}={{M}_{h2}}{{r}_{2}}, \\ & n_{h}^{\left( 2 \right)}={{L}_{h2}}{{n}_{2}}, \\ \end{align} \right.$ | (6) |
| $\left\{ \begin{align} & e_{\text{I}}^{\left( 2 \right)}={{L}_{h2}}e_{f}^{\left( 2 \right)}, \\ & e_{\text{II}}^{\left( 2 \right)}={{L}_{h2}}e_{h}^{\left( 2 \right)}, \\ & k_{\text{I}}^{\left( 2 \right)}=k_{f}^{\left( 2 \right)}, \\ & k_{\text{II}}^{\left( 2 \right)}=k_{h}^{\left( 2 \right)}. \\ \end{align} \right.$ | (7) |
式中: Mh2为大轮坐标系到啮合坐标系的转换矩阵,Lh2为Mh2的旋转矩阵.Mh2可表示如下:
| ${{M}_{h2}}=\left[ \begin{matrix} \cos ~\eta & \sin ~\eta \sin ~\psi _{2}^{\left( M \right)} & \sin ~\eta \cos ~\psi _{2}^{\left( M \right)} & -\cos ~\eta \\ 0 & \cos ~\psi _{2}^{\left( M \right)} & -\sin ~\psi _{2}^{\left( M \right)} & E \\ -\sin ~\eta & \cos ~\eta \sin ~\psi _{2}^{\left( M \right)} & \cos ~\eta \cos ~\psi _{2}^{\left( M \right)} & \sin ~\eta \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right].$ |
式中:η、E分别为大、小轮的轴夹角和偏置距.
3 确定小轮加工参数预置传动比函数的一阶导数m′21 、接触迹线与齿根夹角η2和接触椭圆长半轴长度a,将式(6)和(7)代入文献[1]中点接触齿面间主方向和主曲率的关系公式,可由大轮参考点M处的主方向和主曲率计算出参考点M处小轮齿面的主方向eⅠ(1)、eⅡ(1) 和主曲率kⅠ(1)、kⅡ(1) 以及小轮和大轮第一主方向之间的夹角σ(12).
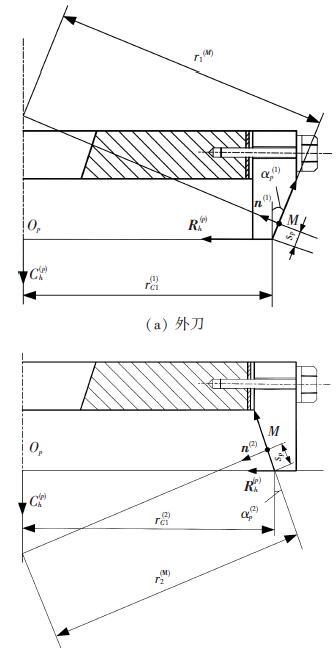
由线接触条件可得相应小轮刀盘锥面的主曲率kⅠ(p)和kⅡ(p)、主方向eⅠ(p) 和eⅡ(p) 以及刀盘锥面和小轮齿面第一主方向的夹角σ(p1).小轮单面刀盘外刀和内刀法截面示意图如图 2(a)和图 2(b)所示,图中r1(M)和r2(M)分别为外刀和内刀参考点M处的曲率半径,Sp为小轮刀盘锥面参数,rc1(1) 和rc1(2) 分别为小轮刀盘外刀和内刀的刀尖半径,Ch(p)为刀盘轴线的单位矢量,n(1)和n(2)分别为外刀和内刀参考点M处的法矢,由此可计算出刀盘刀顶平面中心位置矢量Rh(p).
|
图 2 小轮单面刀盘法截面示意 |
| $\begin{align} & C_{h}^{\left( p \right)}=-e_{I}^{\left( F \right)}\cdot cos~{{\alpha }_{1}}-n_{h}^{\left( 1 \right)}\cdot sin~{{\alpha }_{1}}, \\ & R_{h}^{\left( p \right)}=r_{h}^{\left( 1 \right)}-e_{I}^{\left( F \right)}\cdot ({{S}_{p}}+r_{c1}^{\left( 1 \right)}~sin~{{\alpha }_{1}})+n_{h}^{\left( 1 \right)}\cdot r_{c1}^{\left( 1 \right)}~sin~{{\alpha }_{1}}. \\ \end{align}$ |
式中: Sp为小轮刀盘锥面参数;rh(1) 、nh(1) 为啮合坐标系中小轮的位矢和法矢,且rh(1)=rh(2),nh(1)=nh(2).
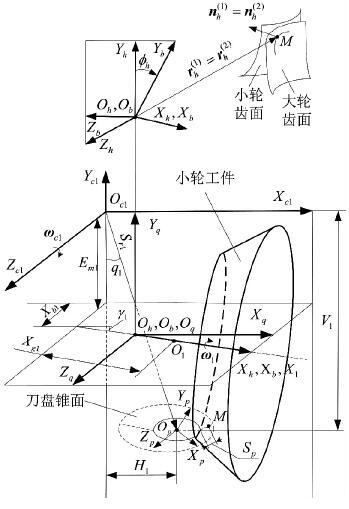
小轮切齿参数设计坐标系如图 3所示.图中Oh-XhYhZh为啮合坐标系,Oc1-Xc1Yc1Zc1为机床坐标系,Op-XpYpZp为小轮刀盘坐标系,O1为小轮的坐标原点,Op为小轮的刀盘中心,φh(为给定值)为小轮初始加工转角,M为参考点,γ1(为给定值)为小轮机床安装角.将rh(2) 、nh(2) 、Ch(p)、Rh(p) 和eⅠ(p)、eⅡ(p) 变换到坐标系Oq-XqYqZq中,得到rq(1)=rq(2),nq(1)=nq(2),以及Cq(p)、Rq(p) 、eqⅠ(p)和eqⅡ(p).坐标变换矩阵Mqh表示如下:
|
图 3 小轮切齿参数设计坐标系 |
| ${{M}_{qh}}=\left[ \begin{matrix} \cos {{\gamma }_{1}} & \sin {{f}_{1}}\sin {{f}_{h}} & \sin ~{{\gamma }_{1}}\cos {{f}_{h}} & 0 \\ 0 & \cos {{f}_{h}} & -\sin {{f}_{h}} & 0 \\ \sin ~{{\gamma }_{1}} & \cos ~{{\gamma }_{1}}\sin {{f}_{h}} & \cos ~{{\gamma }_{1}}\cos {{f}_{h}} & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right].$ |
将rq(1) 、nq(1) 、Cq(p)、Rq(p) 、eqⅠ(p) 和eqⅡ(p) 变换到机床坐标系Oc1-Xc1Yc1Zc1中,得到rc1(1) 、nc1(1) 、Cc1(p)、Rc1(p) 、ec1Ⅰ(p)和ec1Ⅱ(p).坐标转换矩阵Mc1q可表示如下:
| ${{M}_{c1q}}=\left[ \begin{matrix} 1 & 0 & 0 & {{X}_{g1}}\cos ~{{\gamma }_{1}} \\ 0 & 1 & 0 & -{{E}_{m1}} \\ 0 & 0 & 1 & {{X}_{g1}}\sin ~{{\gamma }_{1}} \\ 0 & 0 & 0 & 1 \\ \end{matrix} \right].$ |
小轮和产形轮的啮合方程为
| ${{v}^{(p1)}}\cdot n_{c1}^{\left( 1 \right)}=0$ | (8) |
式中: v(p1)为小轮产形轮和小轮的相对速度;nc1(1)为参考点M处的法矢.
联合文献[1]中基本方程组和式(8)以及rc1(1) 、nc1(1) 、Cc1(p)、Rc1(p) 、eqⅠ(p) 以及eqⅡ(p),将以上过程编制成计算机程序,可得到轴向轮位Xg1、垂直轮位Em1和滚比Cr1,由于篇幅限制,这里不再展开说明.
Rc1(p) 可表示为
| $R_{c1}^{\left( p \right)}=\left[ \begin{matrix} R_{c1x}^{\left( p \right)} & R_{c1y}^{\left( p \right)}~ & R_{c1z}^{\left( p \right)}~ \\ \end{matrix} \right]$ |
所以, 根据图 3,小轮的水平刀位H1、垂直刀位V1、床位Xb1、径向刀位Sr1和角向刀位q1为
| $\begin{matrix} {{H}_{1}}=R_{c1x}^{\left( p \right)}, \\ {{V}_{1}}=R_{c1y}^{\left( p \right)}, \\ {{X}_{b1}}=R_{c1z}^{\left( p \right)}, \\ {{S}_{r1}}={{H}^{2}}_{1}+{{V}^{2}}_{1}~, \\ {{q}_{1}}={{\sin }^{-1}}({{V}_{1}}/{{H}_{1}}). \\ \end{matrix}$ |
另外,小轮的刀倾角i和刀转角j可由刀盘轴线的单位矢量
| $\begin{align} & C_{q}^{\left( p \right)}=\left[ \begin{matrix} C_{qx}^{\left( p \right)} & C_{qy}^{\left( p \right)} & C_{qz}^{\left( p \right)} \\ \end{matrix} \right] \\ & ~ \\ \end{align}$ |
求得:
| $\begin{align} & i={{\sin }^{-1}}(\sqrt{{{(C_{qx}^{\left( p \right)})}^{2}}+{{(C_{qy}^{\left( p \right)})}^{2}}}), \\ & j={{\tan }^{-1}}(-C_{qy}^{\left( p \right)}/C_{qx}^{\left( p \right)}). \\ \end{align}$ |
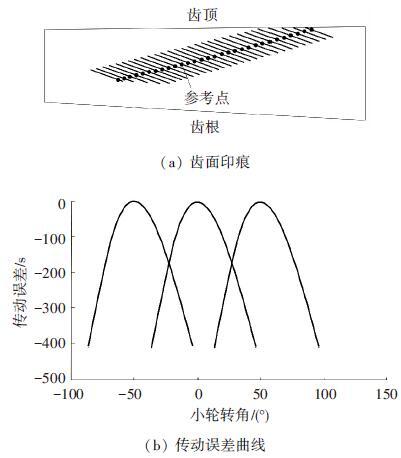
用以上方法对一对HGT准双曲面齿轮副进行切齿参数设计,轮坯参数见表 1,切齿参数见表 2中算例1(小轮采用单面法加工,这里仅列出小轮凹面的加工参数),齿面方程推导见文献[16],TCA[16]分析结果见图 4.局部控制参数为接触迹线与齿根夹角为35°,传动误差曲线斜率为-0.000 4,瞬时接触椭圆长轴占齿宽比例为0.3,参考点齿宽方向控制参数Δx=3 mm,参考点齿高方向控制参数Δy=2 mm,改变参考点的位置,令Δx=3,Δy=2,即令齿面印痕向大端和齿顶移动,此时大轮切齿参数不变,小轮切齿参数见表 2中算例2,TCA分析结果见图 5.
| 表 1 轮坯参数 |
| 表 2 切齿参数 |
|
图 4 算例1的TCA分析结果 |
|
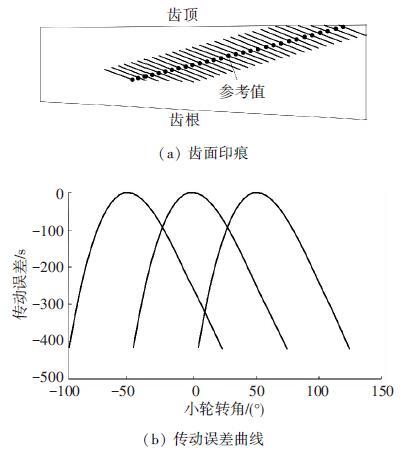
图 5 算例2的TCA分析结果 |
由图 4可以看出,接触迹线接近直线,可避免边缘接触和轮齿齿顶、齿根的应力集中;传动误差幅值较大,且没有出现边缘接触,避免了轮齿传动的振动与冲击,使齿轮传动平稳.
由图 5可知,当参考点位置改变后,齿面印痕也相应随之改变,且接触迹线同样接近直线;传动误差对称并且幅值较大.同理,可通过改变其他局部控制参数得到不同的切齿参数,进而得到不同的齿面印痕和传动误差曲线.
以上分析结果,验证了切齿参数设计的正确性.
5 结论1) HGT准双曲面齿轮大轮采用展成法加工,齿面曲率特性好,能有效改善齿轮的啮合性能,这一点是成形法所不具备的;小轮采用刀倾法加工,可简化刀具规格,使操作调整相对简单,这一点又优于变性法.因此,本文的研究为挖掘目前常见的加工方法,或探索新的加工方法,获得高性能的准双曲面齿轮提供了方法和保证.
2) 确定改善啮合和切触状态的切齿参数是齿轮研究的主要课题,本文以局部综合法为基础,对HGT准双曲面齿轮进行了切齿参数设计,通过控制参考点的一阶和二阶接触参数,达到了对齿面啮合性能的控制.该研究为高精度HGT准双曲面齿轮的设计与加工提供了有效工具.
3) 本文的设计方法保证了齿面接触迹线为直线,可降低对安装误差的敏感性;且保证了接触迹线与齿根有较小的夹角,增大了齿轮副的重合度,使齿轮运转平稳.验证了本文切齿设计方法的正确性.
| [1] |
LITVIN F L.
Gear geometry and applied theory[M]. New York: Cambridge University Press, 2004 : 604 -623.
( 0) 0)
|
| [2] |
FAN Q. Tooth surface error correction for face-hobbed hypoid gears[J].
Journal of Mechanical Design,2010, 132 (1) : 011004.
( 0) 0)
|
| [3] |
FAN Q. Optimization of face cone element for spiral bevel and hypoid gears[J].
Journal of Mechanical Design,2011, 133 (9) : 091002.
( 0) 0)
|
| [4] |
SIMON V V. Advanced manufacture of spiral bevel gears on CNC hypoid generating machine[J].
Journal of Mechanical Design,2010, 132 (3) : 031001.
( 0) 0)
|
| [5] |
SIMON V V. Generation of hypoid gears on CNC hypoid generator[J].
Journal of Mechanical Design,2011, 133 (12) : 121003.
( 0) 0)
|
| [6] |
KAWASAKI K, TSUJI I. Analytical and experimental tooth contact pattern of large-sized spiral bevel gears in cyclo-palloid system[J].
Journal of Mechanical Design,2010, 132 (4) : 041004.
( 0) 0)
|
| [7] |
PARK D, KOLIVAND M, KAHRAMAN A. An approximate method to predict surface wear of hypoid gears using surface interpolation[J].
Mechanism and Machine Theory,2014, 71 : 64-78.
( 0) 0)
|
| [8] |
MOHAMMADPOUR M, THEODOSSIADES S, RAHNEJAT H, et al. Non-Newtonian mixed elastohydrodynamics of differential hypoid gears at high loads[J].
Meccanica,2014, 49 (5) : 1115-1138.
( 0) 0)
|
| [9] |
TAKEDA R, KOMORI M, NISHINO T, et al. Performance analysis of generated hypoid gear based on measured tooth flank form data[J].
Mechanism and Machine Theory,2014, 72 : 1-16.
( 0) 0)
|
| [10] |
SIMON V V. Optimization of face-hobbed hypoid gears[J].
Mechanism and Machine Theory,2014, 77 : 164-181.
( 0) 0)
|
| [11] |
LITVIN F L, ZHANG Y. Local synthesis and tooth contact analysis of face-milled spiral bevel gears[R]. Chicago: University of Illinois, 1991:16-39.
( 0) 0)
|
| [12] |
张华, 邓效忠. 基于局部综合的非零变位弧齿锥齿轮切齿仿真[J].
农业机械学报,2007, 38 (5) : 204-206.
( 0) 0)
|
| [13] |
杨宏斌, 范明, 周彦伟, 等. 高齿准双曲面齿轮的研究[J].
中国机械工程,2000, 11 (8) : 897-900.
( 0) 0)
|
| [14] |
方宗德, 杨宏斌. 准双曲面齿轮的优化切齿设计[J].
汽车工程,1998, 20 (5) : 302-307.
( 0) 0)
|
| [15] |
王星, 方宗德, 李声晋. HGT准双曲面齿轮传动的轮齿接触分析[J].
西北工业大学学报,2014, 32 (3) : 475-480.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


