2. 广东省汽车工程重点实验室,广州 510640
2. Guang Dong Provincial Key Laboratory of Automotive Engineering, Guangzhou 510640, China
在传统的钢结构车身骨架中引入铝合金,开发钢铝混合车身,能进一步实现汽车的轻量化,降低油耗[1-2]. 然而,钢铝板材间运用传统的焊接工艺时,容易出现焊穿、电化学腐蚀等各种缺陷,无法获得可靠的连接性能. 近期出现的压力连接技术可有效应用于连接异种金属板材[3-4],具有无需添加辅助材料等优点,但其连接强度较低. 胶接同样可以用于连接异种金属材料,且具有连接强度大、结构质量轻、抗疲劳强度大等优点[5],国外学者提出压-胶复合连接技术,并开展了相关的研究. 文献[6-7]采取先胶粘固化后压力连接的工艺顺序,进行压-胶复合连接的单搭接试件进行拉伸实验,得出复合连接的强度主要由胶粘剂的性能决定的结论. 文献[8]运用内聚力模型模拟胶粘剂的失效行为,对6061铝合金板件采取压-胶复合连接,获得了与锁铆连接接近的连接效果,分析了压力连接点数量对连接部件耐撞性能的影响. 文献[9]实验比较了压-胶复合连接、锁铆连接以及焊接的连接性能,指出压-胶复合连接在强度和吸收能量方面具有优势. 综上所述,压-胶复合连接能结合压力连接和胶接的优点,具有提高连接强度、安全性以及改善碰撞吸能特性等优点. 目前,国内外对压-胶复合连接技术的研究处于初步阶段,主要围绕同种材料连接的可行性、影响因素、吸能效果等进行研究,而对异种材料的连接特性及优化方法的研究成果并不多见.
本文选取车身使用较多的Q235钢板和A5052铝合金板为连接对象,选取环氧树脂作为胶粘剂;在实验验证的基础上,利用仿真模型建立接头强度的近似模型,并对连接性能进行多目标优化,以获得最佳连接效果.
1 内聚力模型内聚力模型是美国学者Needleman[10]提出的理论体系,其本构关系的核心思想是界面应力取决于界面的相对位移,材料断裂过程中能量耗散的分配由材料性质和驱动力-位移(Traction-Separation)特性曲线共同决定[11]. 常见的裂纹形式多为混合型裂纹,即胶粘剂单元受到拉伸力和剪切力的共同作用,其驱动力-位移特性曲线如图 1所示.
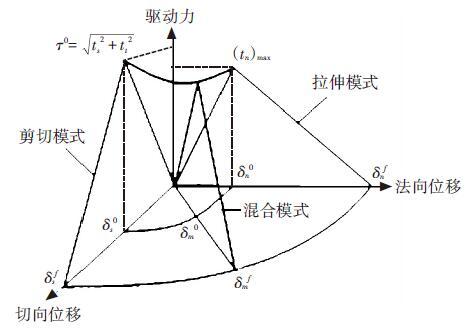
|
图 1 混合型驱动力-位移特性曲线 |
运用内聚力模型模拟胶粘剂的损伤行为,重点在于确立初始损伤准则和失效扩展准则,其中二次应力准则在初始损伤准则中运用广泛,表达式为
| ${{\{\langle {{t}_{n}}\rangle /t_{n}^{0}\}}^{2}}+{{\{{{t}_{S}}/t_{S}^{0}\}}^{2}}+{{\{{{t}_{t}}/{{t}^{0}}_{t}\}}^{2}}=1$ |
式中:tn、ts、tt分别为内聚力单元在法向、切向1和切向2的应力; tn0为内聚力单元单独受到拉伸作用下的法向最大临界应力,ts0、tt0分别为单独受到剪切作用下的切向1、切向2的最大临界应力. 当3个方向上的应力比平方和达到1时,内聚力单元即发生初始损伤.
当初始损伤条件满足后,内聚力单元的损伤行为将由失效扩展准则来控制,直到单元彻底失效. 引入失效退化参数D用于描述内聚力单元的损伤行为,与参数D相关的失效扩展准则定义如下
| $\begin{align} & {{t}_{n}}=\left\{ \begin{matrix} \left( 1-D \right){{{\bar{t}}}_{n}} & {{{\bar{t}}}_{n}}>0, \\ {\bar{t}} & {{{\bar{t}}}_{n}}\le 0, \\ \end{matrix} \right. \\ & {{t}_{s}}=\left( 1-D \right){{{\bar{t}}}_{s}},{{t}_{t}}=\left( 1-D \right){{{\bar{t}}}_{t}}. \\ \end{align}$ |
式中:tn、ts、tt分别为在无损伤情况下,根据当前应变和Traction-Separation特性曲线预测的应力. 随着破坏的进展,D从0向1变化,当D=1时,法向应力和切向应力均为零,此时单元完全破坏失效. 混合模式加载下的失效退化进程以断裂能量为准则,本文运用Benzeggag和Kenane提出的B-K准则[12],表达式如下:
| ${{G}^{C}}=G_{n}^{C}+(G_{S}^{C}-G_{n}^{C}){{\{G{{G}_{S}}/{{G}_{T}}\}}^{\eta }}$ |
式中:GS=Gs+Gt,GT=Gn+Gs以及η=1是与混合程度有关的材料参数,Gn、Gs、Gt分别为内聚力单元沿法向、切向1和切向2做的功;GnC、GSC、GC分别为法向断裂能、切向断裂能和混合断裂能.
2 连接方案 2.1 各种连接方式的拉伸强度比较为了比较压力连接与传统焊接方式存在的差距,制作相关部件进行实验. 制作100 mm×40 mm×1 mm的Q235钢板,采用氩弧焊的方法分别进行对接焊和搭接焊;同时,制作钢铝板材压力连接试件,A5052铝合金板的厚度为1.6 mm. 采用万能材料试验机分别对以上试件进行拉伸破坏,测试其连接强度.
各连接方式的试件及拉伸破坏过程对应的位移-载荷曲线如图 2所示.
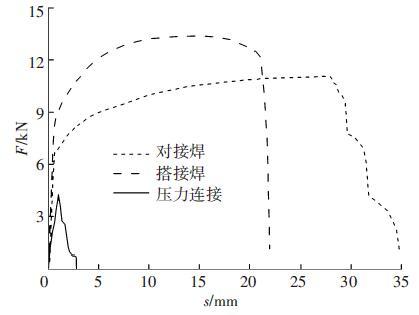
|
图 2 不同连接试件的位移-载荷曲线对比 |
对接焊和搭接焊的破坏强度分别为11.06 kN和13.43 kN;压力连接的剪切破坏强度为4.15 kN,分别达到对接焊和搭接焊强度的37.5%和30.9%,可见简单的压力连接与焊接的性能差距较大,对钢铝板应用更有效的连接方式具有实际意义.
2.2 压-胶复合连接工艺压-胶复合连接可以有两种方案:先压力连接再固化胶层;先固化胶层再压力连接. 由于胶层未固化时,凸模对板材的冲击力会造成胶层厚度的变化,从而影响连接的效果,也使得连接强度更加难以预测. 而先固化再进行压力连接,胶层已经形成结构力学性能,可形成完整的复合连接接头.
本文选取先固化后压力连接的工艺顺序,压力连接时铝板在上钢板在下. 为避免固化后胶层在压力连接区域发生胶层脆裂而降低接头强度的现象,涂胶时在压力连接区域空出半径为4.5 mm的圆形区域,见图 3.

|
图 3 压-胶复合连接的连接工艺顺序 |
被连接板件选取目前车身上使用较多且屈服强度较为接近的A5052铝合金和Q235钢,胶粘剂选取高弹性模量的德国Ergo7200环氧树脂胶粘剂. 相关的材料力学性能表 1、2.
| 表 1 A5052铝合金与Q235钢材料参数 |
| 表 2 Ergo7200环氧树脂胶粘剂材料参数 |
金属材料A5052铝合金与Q235钢通过拉伸试验获得材料的真实应力应变数据,构建材料的本构方程,而环氧树脂胶粘剂运用内聚力模型定义相关参数.
3.2 有限元模型的建立构建钢铝板材压-胶复合连接的单搭接模型和T型连接模型,分别用于测试剪切强度和剥离强度. 单搭接模型选取铝合金板尺寸为100 mm×40 mm×1.6 mm,钢板的尺寸为100 mm×40 mm×1 mm;胶层尺寸为40 mm×40 mm×0.2 mm(压力连接区域空出半径为4.5 mm的圆形区域);T型连接模型中钢铝板材弯折两端的长度均分别为60 mm和40 mm,宽度均为40 mm. 压力连接点位于胶接区域的几何中心处.
在ABAQUS软件中建立仿真模型. 仿真模型具有对称性,为节约计算时间,使用二分之一模型进行计算,如图 4所示. 铝合金板和钢板单元类型为C3D8R,并对压力连接区域进行网格细化;胶层为内聚力单元,类型为COH3D8;为避免因塑性大变形而带来的网格畸变,对压力连接区域的单元采用ALE自适应网格技术[13]. 仿真中对固定端施加固定约束;拉伸端的单元节点与参考点施加捆绑约束,并对参考点施加力F进行匀速拉伸,直至整个连接发生破坏失效;固定端与拉伸端的长度均为30 mm.
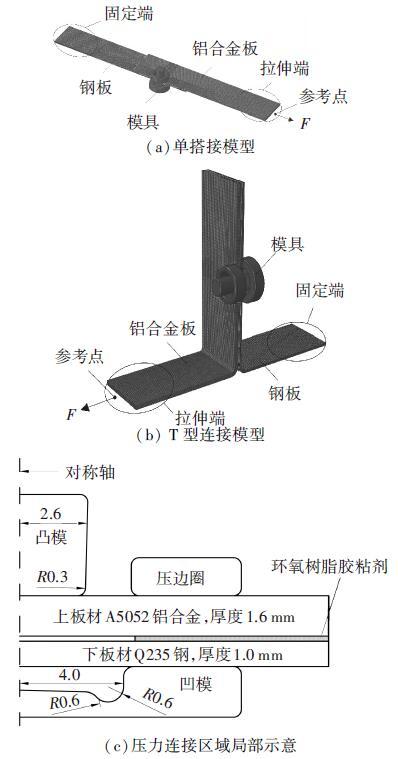
|
图 4 钢铝板材压-胶复合连接有限元模型 |
按照图 3所示的连接工艺进行实验,制作与仿真模型相同规格的试件,同样的单搭接试件和T型连接试件分别用于测试剪切强度和剥离强度. 涂胶前需对连接件进行表面处理,包括机械打磨、清洗以及烘干. 表面处理的目的是避免胶粘剂在实验过程中发生界面脱离而失效,以保证胶粘剂发挥最大作用[14]. 涂胶完成后,将试件置于干燥处在室温下固化48 h. 最后,使用压力连接仪器对钢铝板件进行压力连接,即完成了压-胶复合连接的整个过程.
使用万能材料试验机进行对单搭接试件和T型连接试件进行拉伸,记录对应的位移-载荷数据;两种试件各进行3组以减小误差. 实验后胶层破坏失效,压力连接接头则发生断裂或者剥离,从而导致整个连接的失效. 单搭接试件中的压力连接接头被剪断,而T型试件中压力连接接头则发生剥离. 单搭接接头和T型连接均出现了界面破坏,面积约占连接面的10%. 界面破坏会降低压-胶复合连接的剪切强度和剥离强度.
3.4 仿真与实验对比分析实验及仿真结果如表 3所示. 实验测得钢铝板压-胶复合连接的剪切强度与仿真得到的剪切强度误差分别为5.88%和8.52%,在合理的范围之内. 实验中胶粘剂的失效形式中存在一定程度的界面破坏而降低了连接强度,而仿真模型中胶粘剂的破坏则全部为内聚力破坏,因而实验值略低.
| 表 3 压-胶复合连接仿真与实验结果对比 |
通过实验对比得知,压-胶复合连接的剪切强度达到了相同连接尺寸下对接焊强度的83.7%和搭接焊的68.9%,比简单的压力连接强度提高了一倍以上,可见压-胶复合连接具有更大的连接强度. 为分析胶粘剂在复合连接中发挥的作用,对压-胶复合连接和压力连接的位移-载荷曲线进行对比分析. 对应的位移-载荷曲线如图 5所示.
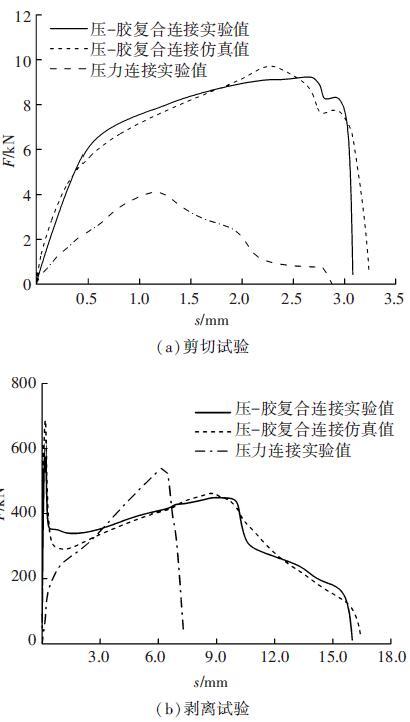
|
图 5 试件拉伸过程位移-载荷曲线对比 |
剪切试验中,压-胶复合连接的拉伸过程在位移0~0.50 mm时主要为钢铝板材发生弹性变形,在0.50~2.00 mm时主要为钢铝板材发生塑性变形;而在2.20~2.70 mm左右时载荷达到最大值后,胶粘剂开始发生破坏,载荷明显下降;在位移为2.75~2.90 mm时主要是压力连接接头起到连接作用,载荷会小幅上升;随着压力连接接头被剪断,载荷迅速下降,整个接头发生破坏. 两种连接方式相比较可以看出,在拉伸位移< 2.50 mm时,胶粘剂将连接区域内的钢板和铝板紧紧地“绑定”在一起,类似于刚性连接,非连接区域从弹性变形阶段进入塑性变形阶段,直至载荷达到胶粘剂的破坏条件,连接开始失效;而压力连接试件从拉伸一开始,接头便受到剪切力作用而变形,当接头被剪断时连接失效.
剥离试验中,压-胶复合连接在位移为0.20 mm左右时胶粘剂发生破坏,载荷达到最大值;在1.00~9.00 mm时主要是压力连接在起连接作用,达到峰值时压力连接接头被剪断或剥离,载荷将明显下降;位移为9.00~16.00 mm时主要为余下的胶粘剂发挥作用,直至整个接头脱离. 压力连接试件在拉伸过程中载荷逐渐增大,待接头脱离或拉断时连接失效. 相比之下,胶粘剂加大了剥离载荷作用时的破坏难度,提高了连接强度. 结合剪切试验和剥离试验可以看出,压-胶复合连接在胶粘剂破坏后压力连接能继续发挥作用,连接完全失效需要更大的载荷和位移,因而提高了连接强度和安全性能.
对比图 5中压-胶复合连接实验与仿真的位移-载荷曲线,得知采用内聚力模型的仿真模型能较为准确地模拟胶粘剂的连接作用和失效行为,因此获取的接头强度可用于后续的优化研究. 同时可看出,压-胶复合连接更容易因为承受剥离载荷而失效,因此后续优化中应更多的考虑连接的剥离强度.
4 压-胶复合连接强度预测与参数的多目标优化 4.1 基于正交试验设计方法的仿真在压力连接模具参数、胶粘剂种类确定的情况下,压-胶复合连接的接头性能可能受到钢铝板材厚度、胶层厚度和板材搭接长度的影响,而压力连接中凸模的下压行程会影响接头的颈厚值和自锁值,从而影响复合连接接头的性能. 以上5个因素均可选取不同的水平,因而可以将强度预测问题看作一个多因素多水平的数学建模问题.
正交试验[15]:选取铝板厚度(x1)、钢板厚度(x2)、胶层厚度(x3)、搭接长度(x4)以及凸模冲程(x5)这5个因素作为分析的设计变量,变量示意如图 6所示;每个因素选取3个水平,如表 4所示. 通过正交试验获取样本点以构造近似模型,预测接头的连接强度,并对接头的剪切强度和剥离强度进行多目标优化.
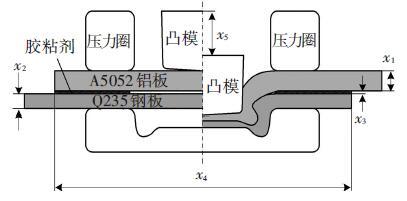
|
图 6 设计变量示意图 |
| 表 4 因素水平表 |
安排L27(313)正交试验,具体安排与仿真结果如表 5所示.
| 表 5 正交试验及仿真结果 |
对27次试验方案的仿真结果进行观察,发现27号试验的压力连接接头没有形成明显的自锁结构,达不到复合连接的效果. 为保证拟合的近似模型具有较高的精确度,采取样本点时去除27号试验,将余下的26组试验用于构建近似模型.
4.2 响应面模型的构建响应面模型通过选取设计空间内一定数量的设计点来构造响应函数作为近似数学模型,利用多项式函数来拟合设计空间,具有收敛速度快和鲁棒性好等特点,是一种较为高效的近似求解方法[16]. 当含有m个设计变量时,其响应面函数可表示为
| $\tilde{y}={{\alpha }_{0}}+\sum\limits_{i=1}^{m}{{{\alpha }_{i}}{{x}_{i}}}+\sum\limits_{i=1}^{m}{{{\alpha }_{ii}}x_{i}^{2}}+\sum\limits_{i=1}^{m-1}{\sum\limits_{j=i+1}^{m}{{{\alpha }_{ij}}{{x}_{i}}{{x}_{j}}.}}$ |
响应面模型的拟合一般用复相系数R2和修正复相系数Radj2来衡量[9],其定义如下:
| $\begin{align} & {{R}^{2}}=\left( \sum\limits_{i=1}^{P}{{{\left( {{{\tilde{y}}}_{i}}-{{{\tilde{y}}}_{i}} \right)}^{2}}} \right)/\left( \sum\limits_{i=1}^{P}{{{\left( {{y}_{i}}-{{{\bar{y}}}_{i}} \right)}^{2}}} \right), \\ & R_{\text{adj}}^{2}=1-\frac{\sum\limits_{i=1}^{P}{{{\left( {{{\tilde{y}}}_{i}}-{{{\bar{y}}}_{i}} \right)}^{2}}\left( p-1 \right)}}{\sum\limits_{i=1}^{P}{{{\left( {{y}_{i}}-{{{\bar{y}}}_{i}} \right)}^{2}}\left( p-k-1 \right)}}. \\ \end{align}$ |
式中:p为样本点数目,k为自由度,yi、${{\tilde{y}}_{i}}$、yi分别为响应量的实测值、预测值以及实测值的平均值. R2和Radj2越接近于1,则表明响应面拟合的精度越高.
对目标函数剪切强度(S)和剥离强度(P)进行拟合,得出其响应面函数表达式为
| $\begin{align} & S= & 94\text{ }731.41-18\text{ }900.51{{x}_{1}}+157.25{{x}_{2}}+ \\ & 13\text{ }359.3{{x}_{3}}-11.62{{x}_{4}}-54\text{ }380.43{{x}_{5}}+ \\ & 3\text{ }090.98x_{1}^{2}+923.56x_{2}^{2}-23\text{ }479.91x_{3}^{2}- \\ & 0.97x_{4}^{2}+8\text{ }974.65x_{5}^{2}+136.51{{x}_{1}}{{x}_{2}}- \\ & 3\text{ }488.98{{x}_{1}}{{x}_{3}}+88.68{{x}_{1}}{{x}_{4}}+2\text{ }923.91{{x}_{1}}{{x}_{5}}, \end{align}$ |
| $\begin{align} & P= & -8\text{ }140.80+3\text{ }919.79{{x}_{1}}+1\text{ }786.75{{x}_{2}}+ \\ & 1\text{ }546.79{{x}_{3}}+0.17{{x}_{4}}+3\text{ }800.28{{x}_{5}}- \\ & 1\text{ }277.27x_{1}^{2}-320.98x_{2}^{2}-1\text{ }145.09x_{3}^{2}+ \\ & 0.02x_{4}^{2}-812.77x_{5}^{2}-854.99{{x}_{1}}{{x}_{2}}- \\ & 715.15{{x}_{1}}{{x}_{3}}-4.21{{x}_{1}}{{x}_{4}}+381.76{{x}_{1}}{{x}_{5}}, \end{align}$ |
经计算,剪切强度的S响应面模型R2为0.989,Radj2为0.975;剥离强度P的响应面模型R2为0.993,Radj2为0.984,可见其拟合的精度比较高,可以用于多目标优化分析.
4.3 遗传算法多目标优化与结果分析在确定了设计变量、目标函数以及约束条件后,建立使剪切强度和剥离强度达到最大值的数学模型. 为保证优化后具有一定的剥离强度,在约束条件多加一项保证剥离强度(P)>570 N. 则多目标优化的具体数学表达式为
设计变量:x1,x2,x3,x4,x5,
目标函数:Max(S),Max(P),
约束条件:1.4≤x1≤1.6,0.8≤x2≤1.2,0.1≤x3≤0.3,30≤x4≤50,≤2.6≤x5≤3.0
P≥570.
在Isight软件中利用多目标遗传算法函数,通过计算得出响应面模型中剪切强度和剥离强度达到最大值时各个变量的取值及其对应的结果,从而得到两者的多目标优化Pareto前沿解集,如图 7所示,并从解集中选出10组列入表 6.
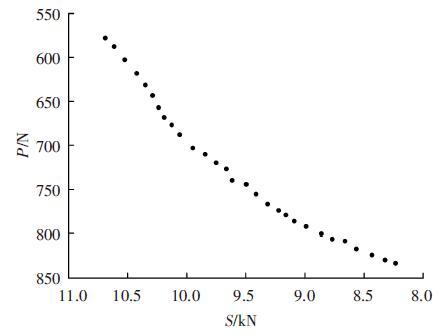
|
图 7 剪切强度与剥离强度的Pareto前沿解集 |
| 表 6 Pareto前沿部分解集 |
由图 7可知,钢铝压-胶复合连接的剪切强度和剥离强度存在一定程度的相互矛盾,有着此消彼长的关系. 表中有部分解集剥离强度过低,而实际应用中,车身连接件会受到各个方向的载荷,因此,在剪切强度本身比较大的情况下,希望寻求剥离强度较大的试验方案. 从表中可以看出,Pareto解集中2号、7号、9号和10号的剪切强度均在9 400 N以上,而剥离强度均在700 N以上,可以优先考虑为综合最优解.
4.4 Pareto 优化解对比验证对选择的4组最优解方案(第2、7、9、10组)通过仿真方法进行验证,其结果如表 7所示.
| 表 7 Pareto优化方案与仿真结果对比 |
结果表明剪切强度的优化方案与仿真结果的最大误差为7.41%,剥离强度的优化方案与仿真结果的最大误差为7.21%,均能够满足工程实际的需求,同时也验证了优化结果的正确性.
5 结论1) 实验对比表明:钢铝压-胶复合连接的剪切强度达到了相同尺寸下钢板焊接强度的70%~80%,并且压-胶复合连接在胶粘剂失效的情况下,压力连接接头能继续发挥作用,说明该连接方式比压力连接具有更大的连接强度和更高的安全性.
2) 仿真模型能较为准确地模拟压-胶复合连接的连接及失效过程,表明了仿真模型的正确性. 使用正交试验的参数组合以及相应的仿真结果,构造二次多项式响应面模型,能较为准确地预测钢铝板材压-胶复合连接的剪切强度和剥离强度.
3) 为获得压-胶复合连接的最佳机械性能,以接头的剪切强度和剥离强度综合达到最大为目标,选取5个影响因素作为设计变量进行多目标优化,得到了关于剪切强度和剥离强度的的Pareto前沿解集. 结果表明多目标优化方法能为压-胶复合连接性能优化提供应用参考.
| [1] |
龙江启, 兰凤崇, 陈吉清. 车身轻量化与钢铝一体化结构新技术的研究进展[J].
机械工程学报,2008, 44 (6) : 27-35.
( 0) 0)
|
| [2] |
ZHOU Y J, LAN F C, CHEN J Q. Crashworthinness research on S-shaped front rails made of steel aluminum hybrid materials[J].
Thin-Walled Structure,2011, 49 (2) : 291-297.
( 0) 0)
|
| [3] |
LEE C J, KIM J Y, LEE S K, et al. Design of mechanical clinching tools for jointing of aluminum alloy sheet[J].
Materials & Design,2010, 31 (4) : 1854-1861.
( 0) 0)
|
| [4] |
DEPAULA. A A, PAGULIAR M T, PERTENCE A E M, et al. Finite element simulation of clinch joining of metallic sheets[J].
Journal of Materials Processing Technology,2007, 182 (1/2/3) : 352-357.
( 0) 0)
|
| [5] |
CHENG J, TAHERI F. A smart single-lap adhesive joint integrated with partially distributed piezoelectric patches[J].
International journal of solid and structures,2006, 43 (5) : 1079-1092.
( 0) 0)
|
| [6] |
BALAWENDER T, SADOWSKI T, KNEC M. Technological problems and experimental investigation of hybrid: clinched-adhesively bonded joint[J].
Archives of Metallurgy and Materials,2011, 56 (2) : 438-446.
( 0) 0)
|
| [7] |
BALAWENDER T, SADOWSKI T, GOLEWSKI P. Numerical analysis and experiments of the clinch-bonded joint subjected to uniaxial tension[J].
Computational Materials Science,2012, 64 : 270-272.
( 0) 0)
|
| [8] |
LEE C J, LEE J M, LEE K H, et al. Development of hybrid clinched structure by using multi-cohesive zone models[J].
International Journal of Precision Engineering and Manufacturing,2014, 15 (6) : 1015-1022.
( 0) 0)
|
| [9] |
MORONI F, PIRONDI A, KLEINER F. Experimental analysis and comparison of the strength of simple and hybrid structural joints[J].
International Journal of Adhesion and Adhesives,2010, 30 (5) : 367-379.
( 0) 0)
|
| [10] |
NEEDLEMAN AA. Continuum model for void nucleation by inclusion debonding[J].
Applied Mechanics,1987 (54) : 525-531.
( 0) 0)
|
| [11] |
BLACKMAN B, HADAVINIA H, KINLOCH A, et al. The use of a cohesive zone model to study the fracture of fiber composites and adhesive-bonded joint[J].
International Journal of Fracture,2003, 119 (1) : 25-46.
( 0) 0)
|
| [12] |
BENZEGGAGH M L, KENANE M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus[J].
Composites Science and Technology,1996, 56 (4) : 439-449.
( 0) 0)
|
| [13] |
黄信宏, 陈吉清, 周云郊, 等. 不同强度钢铝板材压力连接匹配规律与优化[J].
计算机集成制造系统,2012, 18 (5) : 957-964.
( 0) 0)
|
| [14] |
BARTCZAK B, MUCHA J, TRZEPIECINSKI T. Stress distribution in adhesively-bonded joints and the loading capacity of hybrid joints of car body steels for the automotive industry[J].
International Journal of Adhesion & Adhesives,2013, 45 : 42-52.
( 0) 0)
|
| [15] |
方开泰, 马长兴.
正交与均匀试验设计[M]. 北京: 科学出版社, 2001 .
( 0) 0)
|
| [16] |
TANX H, SHEN MF, HOU X L, et al. Response surface method of reliability analysisand its application in slope stability analysis[J].
Geotechnical and Geological Engineering,2013, 31 (4) : 1011-1025.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


