2. 钢铁冶金新技术国家重点实验室(北京科技大学), 北京 100083 ;
3. 北京科技大学 计算机与通讯工程学院, 北京 100083
2. State Key Laboratory of Advanced Metallurgy(University of Science and Technology Beijing), Beijing 100083, China ;
3. School of Computer and Communication Engineering,University of Science and Technology Beijing, Beijing 100083,China
目前,炼钢厂多存在转炉出钢温度过高[1]和钢水温度管控精度低[2]的问题,钢包作为钢水运输容器连接转炉至连铸区段,钢包传热[3]是影响钢水温度的重要因素. 现场温度实测[4]可以定性分析钢包与钢水温度的关系,但由于无法剥离其他非钢包因素的影响,同时由于影响因素的复杂多样性,无法获得精确的规律.Zimmer等[5]使用在包衬内埋设热电偶的方法,估计钢包周转各阶段的包衬温度分布.数值计算能够解析单因素下钢包对钢水温度的影响[6],Camdali等[7]使用稳态传热计算研究LF精炼过程钢包对钢水温降的影响.Tripathi等[8]通过建立CFD模型,结合实验验证的方法研究了钢包包龄对钢水温降影响.杨治立等[9]使用有限元法模拟钢包瞬态传热,并采用能量守恒分析,研究静置和浇铸两阶段内钢包导致的钢水温降值.但若要实现现场应用,需要研究综合因素影响下全工序的钢包热状态和钢水温度变化.
本文使用有限元软件Ansys14和ParaMesh2.3网格随移技术,研究全工序过程中烘烤时间、空包时间、包龄和包衬侵蚀[10]等因素对M钢厂210 t钢包热状态的影响规律,以及复杂钢包热状态对钢水温降的影响,提出了一种基于多因素耦合模拟计算建立钢包分级的方法,实现现场应用.
1 建立传热模型M炼钢厂生产流程包括“转炉—钢包炉精炼—连铸”和“转炉—真空循环脱气精炼—连铸”两种,受生产计划影响,在线周转钢包数量变化范围为6~11包.
1.1 钢包的材质和几何模型钢包高度5.2 m,钢包内腔深度4.06 m,包口外径4.63 m,包口内径4.00 m,钢包有效容积约30 m3,无绝热层.
现场取样实测,获得钢包耐材的热物性参数(见表 1). 钢水等其他热物性参数参阅文献[11].
| 表 1 钢包各层的物性参数 |
由于钢包传热的复杂特性,对其进行以下假设:1)忽略钢包内各层之间的接触热阻[12];2)认为钢包烘烤时煤气燃烧的温度分布均匀;3)忽略钢包各层的热膨胀;4)忽略耳轴、水口和滑板等附件[13];5)认为钢水温度分布均匀,钢包运输过程中钢水温度变化对包衬传热影响较小,温度恒定为1 923 K;6)包盖对钢包包体热状态影响很小,文中忽略;7)钢包为漫射(漫发射、漫反射)灰体.
1.2.1 传热控制方程[14]包衬温度控制方程使用圆柱坐标系下的傅里叶导热微分方程:
| $\rho c\frac{\partial T}{\partial \tau }=\frac{1}{r}\frac{\partial }{\partial r}\left( \lambda r\frac{\partial T}{\partial r} \right)+\frac{\partial }{\partial z}\left( \lambda \frac{\partial T}{\partial z} \right)+\dot{\varphi }.$ |
式中:ρ为包衬材料的密度,kg·m-3;c为包衬材料的比热容,J·kg-1·K-1;T为温度,K;τ为时间,s;φ·为包衬内热源项,W·m-3;r为包壁的半径,m;z为包底的厚度,m;λ为包衬材料的导热系数,W·m-1·K-1.对于钢包有$\dot{\varphi }$=0.
1.2.2 烘烤过程烘烤过程的边界条件包括钢包内壁和钢包外壁的边界条件:
内表面边界条件为
| $\begin{align} & {{Q}_{气-内}}=\left\{ \frac{{{C}_{0}}}{\frac{1}{{{\varepsilon }_{内}}}+\frac{1}{{{\alpha }_{气}}}-1}\left[ \frac{{{\varepsilon }_{气}}}{{{\alpha }_{气}}}{{\left( \frac{{{T}_{气}}}{100} \right)}^{4}}-{{\left( \frac{{{T}_{内}}}{100} \right)}^{4}} \right]+ \right. \left. {{A}_{气-内}}\left( {{T}_{气}}+{{T}_{内}} \right) \right\}{{B}_{内}}; \end{align}$ |
外表面边界条件为
| ${{Q}_{外-环}}={{h}_{外-环}}\left( {{T}_{外}}-{{T}_{环}} \right){{B}_{外}}.$ |
式中:Q气内和Q外环分别为火焰向包衬内表面传递的热量以及包外表面向环境传递的热量,J·s-1;C0为黑体辐射系数,为5.67 W·m-2·K-4;ε内为包衬内表面的黑度;ε气为火焰烟气的黑度;α气为火焰烟气的吸收率;T气、T内、T外、T环为火焰烟气、钢包内外表面和环境的温度,K;A气-内为火焰烟气向钢包内表面的对流换热系数,W·m-2·K-1;B内、B外分别为钢包内、外表面积,m2;h外-环为合并了对流和辐射传热的综合换热系数,W·m-2·K-1.
1.2.3 空包过程空包冷却阶段,认为包内空气是热辐射的透明体,不具有发射和吸收辐射的能力,此阶段钢包内表面的边界条件是
| ${Q_{内 - 环}} = \left\{ {\frac{{{C_0}{\varepsilon _内}{F_{内 - 顶}}}}{{1 - \left( {1 - {\varepsilon _内}} \right)\left( {1 - {F_{内 - 顶}}} \right)}}\left[ {{{\left( {\frac{{{T_内}}}{{100}}} \right)}^4} - {\varepsilon _环}{{\left( {\frac{{{T_环}}}{{100}}} \right)}^4}} \right] - {A_{内 - 环}}\left( {{T_内} - {T_环}} \right)} \right\}{B_内}.$ |
式中:F内-顶为内表面对包顶虚拟面的角系数,ε环为环境的黑度.
钢包外表面的边界条件和烘烤阶段相同.
1.2.4 满包过程[15-16]钢水传热控制方程为
| ${{m}_{钢}}c\left( \frac{\text{d}{{T}_{钢}}}{\text{d}\tau } \right)={{q}_{内壁}}\left( \tau \right){{B}_{内壁}}+{{q}_{内底}}\left( \tau \right){{B}_{内底}}+{{q}_{自}}\left( \tau \right){{B}_{自}}.$ |
满包时内表面的边界条件为
| ${{T}_{内}}={{T}_{钢}}\left( \tau \right),$ |
外表面的边界条件为
| ${{Q}_{外-环}}={{h}_{外-环}}\left( {{T}_{外}}-{{T}_{环}} \right){{B}_{外}}.$ |
式中:m钢为钢水质量,kg;q是热流密度,W·m-2;τ是时间,s;下标:内壁、内底、自分别表示包壁内面、包底内面和钢水渣层自由面.
1.2.5 出钢和浇铸过程边界条件类似于满包过程;浇铸过程可以看成是出钢过程的逆过程,传热边界条件和控制方程和出钢过程类似.
2 计算方法及模型验证 2.1 计算方法根据耐火材料的不同,在有限元软件Ansys14中,将包壳和永久层分别设置为连续的整体,渣线、包壁工作层、包底冲击区工作层、非冲击区工作层、包底砖和围罐砖单独做几何划分,分别对各部分指定不同的耐材特性[17].模型共使用单元28 383个平面4节点热实体单元(PLANE55),对出钢、满包和浇铸过程,使用0~611个表面效应单元(SURF151).使用Paramesh2.3网格随移技术处理钢包壁的侵蚀变薄过程,允许网格有大的移动而仍然保持求解精度.
2.2 模型验证使用红外测温枪对包壳6个不同高度的标记点进行现场测温,与数值模拟结果进行对比验证.测温枪物距比50∶1,精度±1 K.对钢包在上线前烘烤前16 h的升温过程进行了实测值和模拟值的对比. 图 1显示了标记点1和4处的温度变化,标记点1距包底1.4 m,标记点4距包口1.9 m.对包壳6个标记点的温度取平均值,代表包壳的平均温度. 经对比数值计算和实测的误差在4%以内,验证了模型的准确性.
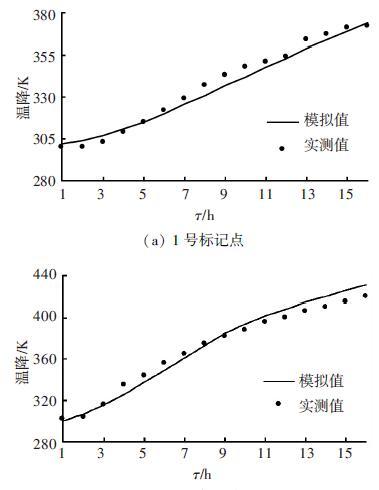
|
图 1 包壳表面测温点温度 |
不同的钢包周转数主要影响钢包烘烤和空包时间,而转炉出钢、精炼、连铸浇注时间以及满包的吊运及等待时间等变化较小,根据对生产数据的统计,钢包周转过程各工序的平均时间为:上线前烘烤10 h、在线烘烤30 min,出钢过程7 min,出钢结束至精炼开始的吊运及等待15 min,精炼30 min,精炼结束至浇注开始的吊运及等待20 min,浇注35 min,空包(浇注结束至在线烘烤开始)60 min.当研究某一过程时间因素的影响规律时,其它过程的时间按以上数据取值.
3.1 上线前烘烤时间的影响模拟不同上线前烘烤时间下,钢包蓄热饱和前包衬的温度变化,并基于能量守恒,计算了每次包龄从转炉出钢至浇铸结束过程钢包对钢水造成的温降值:
| ${{c}_{钢}}{{m}_{钢}}\Delta {{T}_{钢}}=\sum\limits_{i}^{483}{{{q}_{i}}{{B}_{i}}\tau }.$ |
式中:c钢为钢水比热容,J·kg-1·K-1;q为热流密度,W·m-2;ΔT钢是钢水温度变化,K;将与钢水接触的内表面按节点划分为483个微元面,i为每个微元面的序号.
图 2显示了上线前烘烤6~12 h对钢水温降的影响,新包第一个循环周期(第一包龄)造成的钢水温降较大,钢包在周转到第10包龄达到蓄热饱和,造成钢水温降约30 K.烘烤6 h时,第一包龄钢包造成钢水温降约40 K,通过延长烘烤时间,能够有效降低钢水温降,烘烤60 h时,第一包龄钢包造成钢水温降约32 K,已经接近于M炼钢厂钢包蓄热饱和状态下造成的钢水温降值30 K.

|
图 2 不同上线前烘烤时间导致钢水温降 |
M钢厂出钢前钢包于在线烘烤位进行在线烘烤,对空包时间1.0、1.5、2.0、2.5和3.0 h后,在线烘烤0、10、20、30、40 min的钢包后续周转过程进行传热计算.图 3是对钢水温降的影响.空包3 h,不进行在线烘烤时,周转过程钢水温降约47 K;当空包1.5 h,在线烘烤40 min时,周转过程中钢包造成钢水温降是32 K.
在线烘烤前10 min对包衬蓄热的提升较为明显,能够降低后续钢水温降3.1~6.2 K,在线烘烤对降低钢水温降的效果随着烘烤时间增加而减少.
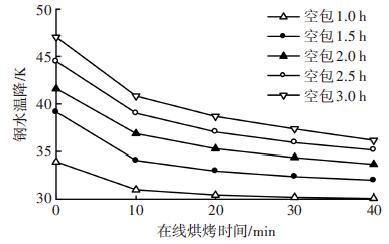
|
图 3 空包和在线烘烤时间对钢水温降的影响 |
生产中,钢包热修完毕后可能进入离线状态,空包等待一段时间,随后进行离线烘烤后再次上线周转.模拟空包1.0、1.5、2.0、2.5和3.0 h,以及每种情况下离线烘烤时间1、3、5、10、20和30 h,研究钢包的包衬温度变化状况和钢水温降,结果见图 4.
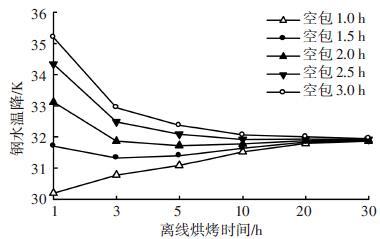
|
图 4 离线烘烤时间对钢水温降的影响 |
图 4表明,当空包1 h时,离线烘烤1 h使后续钢包导致钢水温降约30 K,而增加离线烘烤时间反而会增加钢水温降,这是由于空包时间较短,包衬蓄热较多,钢包的散热量大于离线烘烤给包衬的传热量.当空包时间大于1.5 h时,增加离线烘烤时间有助于减少后续钢水温降,对于不同情况下的钢包,离线烘烤时间大于20 h时对钢水温降的影响不大,随离线烘烤时间延长,钢水温降值趋于约32 K.
3.4 包衬侵蚀的影响钢水和渣[18]的冲刷侵蚀使包衬工作层的厚度逐渐减小.M钢厂在第41和82包龄后对钢包进行小修,包底残厚110 mm,渣线残厚100 mm;第123包龄后进行中修,包底残厚110 mm,包壁残厚90 mm,渣线残厚100 mm;10次中修后进行大修,更换全部永久层和工作层.对一个中修周期(即123包龄),按照工作层平均侵蚀速度,使用网格随移技术更改模型网格的尺寸,模拟钢包周转过程的包衬侵蚀.
图 5显示了第6包和第117包钢包受侵蚀影响的变化,并对比了两者在浇铸开始时刻的包衬温度分布,第117包钢包的渣线、包壁和包底厚度相较第6包明显变薄,同时包壳表面的温度更高.
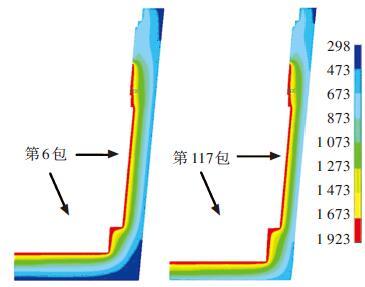
|
图 5 钢包受侵蚀影响温度分布对比(K) |
图 6显示了包衬侵蚀对钢水温降的影响规律,第1包和小修完毕后的第42包、83包,钢水温降分别为36.8、37.1和37.2 K,温降差异很小.蓄热饱和后,第35包、76包和117包,钢包造成的钢水温降为30.1、30.7和31.1 K,侵蚀对蓄热饱和钢包导致钢水温降的影响较小,最高为1 K,其原因是虽然侵蚀包的包壳外表面散热量大,但由于侵蚀使包衬质量减少,而导致包衬蓄热量减少,两种因素互为抵消,它们的综合作用使钢水通过钢包损失的热量相差不大.
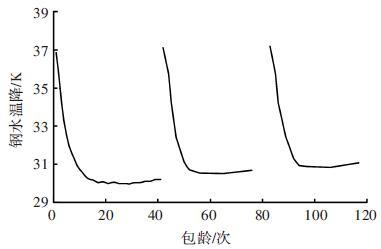
|
图 6 包衬侵蚀对钢水温降的影响 |
钢包分级信息编码按照对钢包蓄热状态影响的4类因素进行分位编排:
1) 上线前烘烤时间. 钢包未达蓄热饱和,根据上线前烘烤时间6、8、…、60 h的模拟结果,对应钢包第1位分级编码A、B、…、I,对于蓄热饱和状态的钢包,其第1位钢包信息编码为O.
2) 包龄和包衬侵蚀[19]. 不同烘烤时间对应钢包达到蓄热饱和的周转次数不同,编码第1位A~I对应的蓄热周期有1~10、1~9、1~8、1~7、1~6、1~5包这几种情况,该包龄为第2位编码,编码对应了包龄对钢水温降的模拟结果;第1位编码为O的钢包,即蓄热饱和的钢包,此时X、Y、Z为第2位编码,表征 1~41、42~82、83~123包的侵蚀影响,X、Y、Z分别对应钢水补偿温降为0、0.5、1.0 K. 1、2位信息编码详情见表 2.
| 表 2 钢包分级第1、2位编码信息 |
3) 空包时间. 第3位信息编码A~E,表示空包时间1.0、1.5、2.0、2.5、3.0 h,编码根据相关模拟结果对应钢水温降值.
4) 在线烘烤和离线时间. 第4位信息编码Z0、Z1、Z2、Z3、Z4,表示在线烘烤0、10、20、30、40 min,编码根据在线烘烤时间影响的模拟结果对应钢水温降值;若钢包转为离线烘烤,第4位信息编码为L1、L2、L3、L4,表示离线烘烤1、3、5、20 h,对应离线烘烤的模拟结果中的钢水温降值.
4.1.2 多因素耦合分级对4类分级编码对应的包况进行数值模拟,计算对钢包热状态和钢水温降的耦合影响,则有
| $\begin{align} & {{T}_{补偿}}={{T}_{降温}}-{{T}_{标}}, \\ & {{T}_{叠加}}=\left( {{T}_{1}}-{{T}_{标}} \right)+\left( {{T}_{2}}-{{T}_{标}} \right). \\ \end{align}$ |
式中:T温降和T补偿是4类影响因素耦合影响下钢包导致钢水温降值和温度补偿值,T标是M炼钢厂蓄热饱和钢包的包衬传热导致钢水温降值,其值为30 K,T1是包龄和上线前烘烤因素影响钢包导致钢水温降值,T2是空包时间和在线烘烤或离线烘烤时间影响导致钢水温降值,T叠加是4类因素两两耦合后钢水温度补偿值的线性叠加.
由于4类因素组合情况非常多,直接计算全部的T补偿工作量巨大,难以实现;而计算T叠加只需分别计算两种因素耦合情况并进行叠加,计算量大大降低.比较T叠加与T补偿,计算其误差,当其他因素固定时,误差随包龄增加而减小,部分编码的误差值详见表 3,当误差<0.1 K时,用T叠加近似代替T补偿.
| 表 3 部分信息编码的T叠加与T补偿的误差值 |
在数值计算中,选取离散有限的特征时间代表一定范围内的烘烤或空包时间,并结合包龄等影响因素,建立包含钢水温度补偿信息的完整钢包分级信息表.信息表集成在钢包信息管理软件中,通过包况实时自动判断钢包等级,提供钢包导致的钢水温度补偿信息,为现场配包提供判据.
表 4根据3 760组现场生产数据,比较使用前后平均转炉出钢温度和精炼废钢使用量(由于钢水温度过高,经常需要在精炼过程添加废钢以降低钢水温度),钢包分级使用后主要钢种的平均出钢温度有明显的下降,下降值在2.3~13.2 K间,出钢温度的降低使精炼加入废钢量明显减少,减少0.18~1.44 t.
| 表 4 钢包分级使用效果对比 |
1) 使用有限元方法建立周转各工序的钢包传热模型,计算了多种因素对钢包热状态和钢水温降的影响规律.上线前烘烤时间由6 h增加至60 h时,第1包龄钢包造成钢水温降值由39.6 K降低至32 K.不同空包时间,前10 min的在线烘烤能减少钢水温降3.1~6.2 K.空包时间大于11.5 h时,增加离线烘烤时间有助于减少钢水温降.
2) 使用网格随移方法计算钢包侵蚀对传热影响. 包衬侵蚀变薄对钢包造成钢水温降值影响较小,侵蚀造成的钢水温降增加最多为1 K.
3) 通过对钢水温度补偿值的叠加和直接计算结果的误差分析,减少了多因素耦合计算的工作量,实现了全因素耦合影响下钢包热状态和钢水温降规律的计算.
4) 考虑包龄、上线前烘烤时间、空包时间、在线和离线烘烤时间的耦合影响,基于数值计算,从造成钢水温降的角度完成钢包热状态分级,钢包的信息编码和分级表应用于M钢厂钢包管理系统,指导配包和钢水温控,降低不同钢种的转炉出钢温度2.3~13.2 K,减少精炼废钢使用量0.18~1.44 t.
| [1] |
余亮, 文光华, 唐萍, 等. 数据挖掘在出钢过程钢水温降预测中的应用[J].
过程工程学报,2009, 9 (1) : 296-299.
( 0) 0)
|
| [2] |
DORCAK L, TERPAK J. Monitoring and prediction of the liquid steel temperature in the ladle and tundish[J].
Metalurgija,2006, 45 (2) : 93-96.
( 0) 0)
|
| [3] |
PAN Yuhua, BJORKMAN B. Physical and mathematical modeling of thermal stratification phenomena in steel ladles[J].
ISIJ International,2002, 42 (6) : 614-623.
( 0) 0)
|
| [4] |
贺东风, 徐安军, 吴鹏飞, 等. 炼钢厂钢包热状态跟踪模型[J].
北京科技大学学报,2011, 33 (1) : 110-115.
( 0) 0)
|
| [5] |
ZIMMER A, LIMA A N C, TROMMER R M, et al. Heat Transfer in Steelmaking Ladle[J].
Journal of Iron and Steel Research International,2008, 15 (3) : 11-14.
( 0) 0)
|
| [6] |
FREDMAN T P. Heat transfer in steelmaking ladle refractories and steel temperature[J].
Scandinavian Journal of Metallurgy,2000, 29 (6) : 232-258.
( 0) 0)
|
| [7] |
CAMDALI U, TUNC M. Steady state heat transfer of ladle furnace during steel production process[J].
Journal of Iron and Steel Research International,2006, 13 (3) : 18-20.
( 0) 0)
|
| [8] |
TRIPATHI A, SAHA J K, SINGH J B, et al. Numerical simulation of heat transfer phenomenon in steel making ladle[J].
ISIJ International,2012, 52 (9) : 1591-1600.
( 0) 0)
|
| [9] |
杨治立, 朱光俊, 王宏丹, 等. 210 t钢包钢水温降规律的数值模拟[J].
炼钢,2011, 27 (2) : 61-64.
( 0) 0)
|
| [10] |
蒋国璋, 孔建益, 李公法, 等. 钢包内衬膨胀缝对热应力的影响研究[J].
中国冶金,2007, 17 (12) : 25-27.
( 0) 0)
|
| [11] |
李红霞.
耐火材料手册[M]. 北京: 冶金工业出版社, 2007 : 710 -711.
( 0) 0)
|
| [12] |
VOLKOVA O, JANKE D. Modelling of temperature distribution in refractory ladle lining for steelmaking[J].
ISIJ International,2003, 43 (8) : 1185-1190.
( 0) 0)
|
| [13] |
LI Gongfa, LIU Jia, JIANG Guozhang, et al. Numerical simulation of temperature field and thermal stress field in the new type of ladle with the nanometer adiabatic material[J].
Advances in Mechanical Engineering,2015, 7 (4) : 1-13.
( 0) 0)
|
| [14] |
徐安军. 炼钢厂物流调控系统及其温度-时间流的解析与应用研究[D].北京:北京科技大学,1996:91-94.
( 0) 0)
|
| [15] |
GILDARDO S D, RODOLFO D M, JOSE B S, et al. Numerical modelling of dissipation phenomena in a new ladle shroud for fluidynamic control and its effect on inclusions removal in a slab tundish[J].
Steel Research International,2014, 85 (5) : 863-874.
( 0) 0)
|
| [16] |
SCHALK W P, EKSTEEN J J, BRADSHAW S M. A numerical modelling investigation into design variables influencing mixing efficiency in full scale gas stirred ladles[J].
Minerals Engineering,2013, 46-47 : 16-24.
( 0) 0)
|
| [17] |
NATH N K, MANDAL K, SINGH A K, et al. Ladle furnace on-line reckoner for prediction and control of steel temperature and composition[J].
Ironmaking & Steelmaking,2006, 33 (2) : 140-150.
( 0) 0)
|
| [18] |
张艳奎, 韩兵强, 邱文冬, 等. 不同Al2O3含量的镁铝尖晶石抗钢包渣侵蚀性研究[J].
耐火材料,2013, 47 (2) : 92-96.
( 0) 0)
|
| [19] |
GRUBER D, HARMUTH H. Durability of brick lined steel ladles from a mechanical point of view[J].
Steel Research International,2008, 79 (12) : 913-917.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


