近年来,协同攻击技术因其在突破防御系统和对目标打击效能等方面相比单系统攻击具有显著优势而受到越来越多学者的关注[1-4]。制导炮弹大量弹体空间用于搭载制导控制系统,导致单发弹杀伤能力有限,为实现精确打击的同时具备足够打击效能,多弹同时弹着协同攻击是最好的策略之一[5]。轨迹优化可以最佳地匹配飞行器各子系统,有利于提高飞行器飞行品质,以最优性能指标实现既定任务[6],因此制导炮弹协同方案弹道的规划对其实现最终对目标的协同攻击具有至关重要的现实意义。
飞行器协同轨迹规划问题本质上可以看作非线性最优控制问题。最优控制问题的求解方法,按照是否给出解析解,可以分为解析法和数值解法。解析法是根据具体问题建立Hamilton函数,构建包含状态方程和协态方程的正则方程,之后根据极值条件和边界条件推导出解析解。解析法精度高、速度快,但是推导过程复杂,仅适用于简单最优控制问题。随着最优控制理论和计算机科学的发展,数值方法成为学者们求解最优控制问题最重要的工具之一。数值方法又分为间接法和直接法。间接法主要是利用庞特里亚金最小原理推导一阶必要最优条件,将原最优控制问题转换为两/多点边值问题,然后通过数值方法求解边值问题得到数值解。史金光等[7]针对滑翔增程制导炮弹的滑翔段方案弹道规划问题,利用变分法推导纵向平面内最优滑翔飞行的两点边值问题,并采用梯度法求解,规划了最远滑翔距离方案弹道。孙瑞胜等[8]利用变分法推导乘波体滑翔飞行器的两点边值问题,然后采用遗传算法解得最大飞行距离方案弹道。间接法的优点是解的精度高,但存在对初值预测敏感的缺陷[9]。直接法是通过某种方法,直接离散最优控制问题中的控制和/或状态变量,将最优控制问题转换为非线性规划问题求解[10]。胡朝江等[11]离散控制变量,采用直接多重打靶法规划飞机的最优着陆轨迹。Subchan等[12]采用直接多重打靶法规划导弹的最短飞行时间最优轨迹。陈琦等[13]采用Gauss伪谱法离散滑翔制导炮弹纵向平面内弹道模型,将无限维最优控制问题转换为有限维非线性规划问题,之后采用序列二次规划算法求解,规划制导炮弹飞行耗时最短方案弹道。徐秋坪[14]结合hp自适应Radau伪谱法和序列二次规划算法,规划出滑翔制导炮弹“滑翔-机动复合效率”最优方案弹道。
针对复杂度较高的协同飞行轨迹优化问题,直接法中的伪谱法由于其求解精度高、收敛速度快,以及避免显式数值积分等优点,使其成为学者们最优先选择的工具之一[14]。Liu等[15]基于Gauss伪谱法规划反舰导弹从指定方位协同攻击敌方舰艇的协同方案弹道。Gu等[16]基于高斯伪谱法规划了多无人机规避禁飞区的协同飞行轨迹。Zhao等[17]采用多基多旅行商方法分配无人机任务,之后根据分配的任务采用Gauss伪谱法规划最优飞行轨迹。许强强等[18]针对面向突防任务的多导弹协同弹道规划问题,采用hp-自适应Radau伪谱法规划了雷达探测威胁最小协同方案弹道。刘超越等[19]采用Gauss伪谱法规划双脉冲导弹的多阶段协同方案弹道。李征等[20]基于Radau伪谱法采用设计“预测-协调-轨迹生成”三步式算法规划可重复使用航天器(reusable launch vehicle, RLV)的协同再入飞行轨迹。
上述文献采用的协同飞行轨迹算法可以分为分布式-协同弹道规划算法(distributed collaborative trajectory programming method, D-CTPM)架构[17-20]和传统集中式-协同弹道规划算法(traditional centralized collaborative trajectory programming method, TC-CTPM) 架构[15-16]。分布式算法架构以某种方法获得或直接指定协同攻击时间,各飞行器按照协同时间规划末端时间固定的飞行轨迹作为协同飞行轨迹。这种算法架构解得的性能指标受协同时间获取方式影响较大,且难以保证协同性能指标的最优性。传统集中式算法架构是联立参与协同飞行的所有飞行器的动态方程为协同动态方程,通过一次求解获得协同方案弹道。传统集中式算法架构的协同时间通过优化解得,求得的协同性能指标在协同动态模型约束下是最优的,然而,联立协同动态方程组的处理方式自动默认约束各飞行器对应阶段的切换时间相等。这一等式约束在处理单阶段轨迹优化问题时没有不利影响,但在求解多阶段制导炮弹弹道规划问题时就显得冗余,这一冗余约束会对协同飞行轨迹的性能指标产生不利影响。此外,传统集中式算法架构还存在一个较大的缺陷,联立的协同弹道规划问题,变量规模庞大,问题的复杂度较高,求解耗时长。
针对分布式算法架构和传统集中式算法架构的不足,本文提出一种增广集中式协同弹道规划算法(augmented centralized collaborative trajectory programming method,AC-CTPM),首先基于多阶段Radau伪谱法,参照分布式算法(D-CTPM)架构分别建立每发制导炮弹的多阶段弹道规划模型,然后扩展组合已建立的各发制导炮弹的多阶段弹道规划模型联立成为一个协同弹道规划问题进行求解。为了提高问题的求解效率,求解之前,以各发弹发射点为原点建立各自2D地面坐标系,采用简化的2D弹道模型快速规划出每发弹的2D标称方案弹道,通过扩展以及坐标转换生成协同弹道规划问题的初始预测。最后以单炮多发制导炮弹协同攻击场景和多炮单发制导炮弹协同攻击场景为仿真算例,验证本文所提AC-CTPM算法的有效性以及相比D-CTPM算法和TC-CTPM算法的优越性。
1 协同弹道规划模型 1.1 火箭助推滑翔增程制导炮弹三维弹道模型参考文献[21],建立3D质点弹道模型:
| $ \left\{\begin{array}{l} \dot{v}=\frac{F_{\mathrm{p}}-F_{x}-m g \sin \theta}{m} \\ \dot{\theta}=\frac{F_{y}-m g \cos \theta}{m v} \\ \dot{\psi}_{\mathrm{v}}=-\frac{F_{z}}{m v \cos \theta} \\ \dot{x}=v \cos \theta \cos \psi_{\mathrm{v}} \\ \dot{y}=v \sin \theta \\ \dot{z}=-v \cos \theta \sin \psi_{\mathrm{v}} \\ \dot{m}=-m_{\mathrm{c}} \end{array}\right. $ | (1) |
式中: v为速度,θ为弹道倾角,ψv为弹道偏角,m为弹体质量,mc为助推火箭单位时间质量流量,Fp为助推火箭推力,Fx为气动阻力,Fy为气动升力;Fz为气动侧向力,(x, y, z)为炮弹在地面坐标系中的坐标。于是该模型的状态向量可以表示为
3个方向的空气动力为
| $ \left\{\begin{array}{l} F_{x}=\frac{1}{2} \rho v^{2} S C_{x 0}\left(1+k_{\mathrm{c}}\left(\alpha^{2}+\beta^{2}\right)\right) \\ F_{y}=\frac{1}{2} \rho v^{2} S C_{y \alpha} \alpha \\ F_{z}=\frac{1}{2} \rho v^{2} S C_{z \beta} \beta \end{array}\right. $ | (2) |
式中:ρ为空气密度,S为参考面积,Cx0为零升阻力系数,Cyα为升力系数导数,Czβ为侧向力系数导数,kc为与诱导阻力相关的系数。等效攻角α和等效侧滑角β作为控制量,为了简便,本文后续简称攻角和侧滑角,于是控制向量可以表示为
根据滑翔增程制导炮弹飞行过程中各阶段飞行特性,将滑翔增程制导炮弹的飞行轨迹分为起飞段、助推段、上升段、滑翔段和末制导段5个阶段,如图 1所示。

|
图 1 滑翔增程制导炮弹弹道示意 Fig. 1 Gliding extended range guided projectile trajectory diagram |
假设参与协同攻击的一组制导炮弹包含np发制导炮弹,为方便标注每一段的时间变量,定义第ip发制导炮弹的第kp阶段持续时长为
| $ \begin{equation*} t_{\mathrm{d}, l_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}=t_{f, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}-t_{0, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}, \left(i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}} ; k_{\mathrm{p}}=1, \cdots, 5\right) \end{equation*} $ | (3) |
式中:
弹道中各阶段定义如下(这里不需区分具体某一发制导炮弹,故变量省略下标ip):
1) 起飞段。始于发射位置,结束于助推火箭点火位置,这一阶段的飞行时间区间为[t0(1), t(1)f]。助推火箭必须在炮弹出炮口一定距离之后才能点火,所以td(1)的下界应设置为一个合适的正数。
2) 助推段。始于助推火箭点火位置,结束于助推火箭关闭位置,这一阶段的飞行时间区间为[t0(2), tf(2)]。td(2)等于助推火箭的工作时间。
3) 上升段。始于助推火箭关闭点,结束于滑翔起始点,这一阶段的飞行时间区间为[t0(3), tf(3)]。现实中,助推火箭由工作状态切换为关闭状态这一扰动在一定程度上会影响弹体平衡,所以助推段结束后需要经过一段时间,等炮弹恢复平衡再开启控制舵进入滑翔段,因此td(3)的下界应设置为一个合适的正数。
4) 滑翔段。始于滑翔起始位置,结束于导引头开启点,这一阶段的飞行时间区间为[t0(4), tf(4)],这一阶段为有控段,制导炮弹可在这一阶段根据协同约束机动飞行,调整飞行轨迹和飞行时间。
5) 末制导段。始于导引头开启点,结束于目标点,这一阶段的飞行时间区间为[t0(5), tf(5)]。
1.3 约束条件 1.3.1 边界约束设第ip发制导炮弹初始质量为m0, ip,初速为v0, ip,起始点坐标为(x0, ip, y0, ip, z0, ip)。于是建立制导炮弹的协同初始状态约束为
| $ \left\{\begin{array}{l} v\left(t_{0, i_{\mathrm{p}}}^{(1)}=v_{0, i_{\mathrm{p}}}\right. \\ x\left(t_{0, i_{\mathrm{i}}}^{(1)}=x_{0, i_{\mathrm{p}}}\right. \\ y\left(t_{0, \mathrm{i}_{\mathrm{p}}}^{(1)}\right)=y_{0, i_{\mathrm{p}}} \\ z\left(t_{0, i_{\mathrm{p}}}^{(1)}=z_{0, i_{\mathrm{p}}}\right. \\ m\left(t_{0, i_{\mathrm{p}}}^{(1)}\right)=m_{0, i_{\mathrm{p}}} \end{array}\right. $ | (4) |
设第ip发制导炮弹攻击的目标坐标为(xt, ip, yt, ip, zt, ip),为对目标实现一定的打击效果,假设末速度不小于vfL,落角不大于θfU。于是末状态约束为
| $ \left\{\begin{array}{l} x\left(t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}\right)=x_{\mathrm{t}, i_{\mathrm{p}}} \\ y\left(t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}\right)=y_{\mathrm{t}, i_{\mathrm{p}}} \\ z\left(t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}\right)=z_{\mathrm{t}, i_{\mathrm{p}}} \\ \theta\left(t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}\right) \leqslant \theta_{\mathrm{fU}} \\ v\left(t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}\right) \geqslant v_{\mathrm{fl}} \end{array}\right. $ | (5) |
火箭助推滑翔增程制导炮弹在不同飞行阶段具有不同的飞行特征,受到不同的约束。助推火箭只在助推段工作,控制量在前3个飞行阶段为零。同一型号制导炮弹过程约束相同,所以不区分具体某一发制导炮弹的弹道诸元,省略制导炮弹序号ip。
1) 上升段和爬升段:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=0 \\ m_{\mathrm{c}}=0 \\ \alpha=0 \\ \beta=0 \end{array}\right. $ | (6) |
2) 助推段:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=F_{\mathrm{p}}^{*} \\ \alpha=0 \\ \beta=0 \end{array}\right. $ | (7) |
式中Fp*为助推火箭的平均推力。
3) 滑翔段和末制导段:
| $ \left\{\begin{array}{l} F_{\mathrm{p}}=0 \\ m_{\mathrm{c}}=0 \\ \alpha_{\min } \leqslant \alpha \leqslant \alpha_{\max } \\ \beta_{\min } \leqslant \beta \leqslant \beta_{\max } \end{array}\right. $ | (8) |
多弹协同弹道规划,需要保证每一发制导炮弹自身的时间连续性和状态变量连续性,即
| $ \left\{\begin{array}{l} t_{\left.\mathrm{f}, i_{\mathrm{p}}\right)}^{\left(k_{\mathrm{p}}\right)}=t_{0, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}+1\right)} \\ \boldsymbol{x}_{\mathrm{f}, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}=\boldsymbol{x}_{0, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}+1\right)} \end{array}\right. $ | (9) |
式中:kp=1, …, 4;ip=1, …, np。
1.3.4 末制导路径约束协同攻击的实现需要调整攻击时间和攻击角度。在末制导段调整攻击时间和攻击角度可能会导致飞行轨迹变得高度弯曲,导致目标脱离导引头视场[22]。因此,在末制导段根据导引头视场角大小建立路径约束至关重要。
制导炮弹末制导过程的几何关系图如图 2所示,其中Mip为第ip发制导炮弹,Tip为第ip发制导炮弹攻击的目标,对应的视线高低角和视线方位角分别为θL, ip和φL, ip。

|
图 2 三维制导几何关系图 Fig. 2 3D guidance geometry diagram |
末制导过程中,小角度假设条件下可以近似认为导引头基准轴和速度轴重合[23-24],则第ip发制导炮弹的弹目视线在高低和方位两个方向相对导引头基准轴线偏离角分别为
| $ \left\{\begin{array}{l} e_{\theta, i_{\mathrm{p}}}=\left|\theta_{i_{\mathrm{p}}}^{(5)}-\theta_{\mathrm{L}, i_{p}}\right| \\ e_{\varphi, i_{\mathrm{p}}}=\left|\psi_{v, i_{\mathrm{p}}}^{(5)}-\varphi_{\mathrm{L}, i_{\mathrm{p}}}\right| \end{array}\right. $ | (10) |
其中视线角公式为
| $ \left\{\begin{array}{l} \theta_{\mathrm{L}, i_{\mathrm{p}}}=\tan ^{-1}\left(\frac{y_{\mathrm{t}, i_{\mathrm{p}}}-y_{i_{\mathrm{p}}}}{\sqrt{\left(x_{\mathrm{t}, i_{\mathrm{p}}}-x_{i_{\mathrm{p}}}\right)^{2}+\left(z_{\mathrm{t}, i_{\mathrm{p}}}-z_{i_{\mathrm{p}}}\right)^{2}}}\right) \\ \varphi_{\mathrm{L}, i_{\mathrm{p}}}=-\tan ^{-1}\left(\frac{z_{\mathrm{t}, i_{\mathrm{p}}}-z_{i_{\mathrm{p}}}}{x_{\mathrm{t}, i_{\mathrm{p}}}-x_{i_{\mathrm{p}}}}\right. \end{array}\right. $ |
式中:ip=1, …, np。
末制导过程中,必须保证目标在导引头视场内。设某型号制导炮弹的导引头的视场角为ε,则第ip发制导炮弹的视场角约束为
| $\left\{\begin{array}{l} e_{\theta, i_{\mathrm{p}}} \leqslant \varepsilon \\ e_{\varphi, i_{\mathrm{p}}} \leqslant \varepsilon \end{array}\right. $ | (11) |
理想的末制导起始点为制导炮弹与目标距离等于导引头最大探测距离的点,过早开启导引头无法探测到目标,过晚开启导引头会减少制导炮弹调整飞行轨迹的可用时间和空间。设该型号制导炮弹导引头最大探测距离为Rs,(x0, ip(5), y0, ip(5), z0, ip(5))为第ip发制导炮弹的方案末制导起始点,则对应的末制导起始点约束为
| $ \begin{equation*} \sqrt{\left(x_{0, i_{\mathrm{p}}}^{(5)}-x_{\mathrm{t}, i_{\mathrm{p}}}\right)^{2}+\left(y_{0, i_{\mathrm{p}}}^{(5)}-y_{\mathrm{t}, i_{\mathrm{p}}}\right)^{2}+\left(z_{0, i_{\mathrm{p}}}^{(5)}-z_{\mathrm{t}, i_{\mathrm{p}}}\right)^{2}}=R_{\mathrm{s}} \end{equation*} $ | (12) |
制导炮弹的协同攻击策略分很多种,包括单炮多发制导炮弹同时弹着攻击一个目标,单炮多发制导炮弹同时攻击多个目标,多炮单发制导炮弹同时攻击一个目标,多炮单发制导炮弹同时攻击多个目标,此外还有采用时间序列依次弹着攻击,以及根据打击任务需求从指定攻击角协同攻击等,针对不同协同策略需要建立不同协同约束。本文采用从指定方位同时弹着策略攻击指定目标,于是建立协同约束如下:
1) 时间协同约束:
| $ \begin{equation*} t^{*}=t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}, \left(i_{\mathrm{p}}=1, 2, \cdots, n_{\mathrm{p}}\right) \end{equation*} $ | (13) |
式中:t*为协同时间,tf, ip(5)为第ip发制导炮弹的弹着时间。
2) 攻击方位角协同约束:
| $ \begin{equation*} \psi_{\mathrm{vf}, i_{\mathrm{p}}}^{(5)}=\psi_{\mathrm{v}, i_{\mathrm{p}}}^{*}, \quad\left(i_{\mathrm{p}}=1, 2, \cdots, n_{\mathrm{p}}\right) \end{equation*} $ | (14) |
式中:ψv, ip*为第ip发制导炮弹被指定的协同攻击方位角,ψvf, ip(5)为第ip发制导炮弹的弹着时刻方位角。
1.4 协同目标函数滑翔增程制导炮弹第4阶段和第5阶段为无动力飞行,控制能力较弱,为减小方案弹道对控制系统的要求,为制导控制系统预留更多机动裕量,目标函数的设计希望使控制量尽量远离上、下界,于是本文设计第ip发制导炮弹的第kp阶段性能评价指标为
| $ \begin{align*} & J_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}=\int_{\substack{t_{i}\left(k_{\mathrm{p}}\right) \\ 0, i_{\mathrm{p}}}}^{t_{\left.f, i_{\mathrm{p}}\right)}^{\left(k_{\mathrm{p}}\right.}}\left(\frac{\alpha_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}}{\alpha_{\text {max }}}\right)^{2}+\left(\frac{\beta_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}}{\beta_{\text {max }}}\right)^{2} \mathrm{~d} t, \\ & \left(i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}} ; k_{\mathrm{p}}=1, \cdots, 5\right) \end{align*} $ | (15) |
第ip发制导炮弹的性能评价指标可以表示为
| $ \begin{align*} & J_{i_{\mathrm{p}}}=\sum\limits_{k_{\mathrm{p}}=1}^{5} J_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}=\sum\limits_{k_{\mathrm{p}}=1}^{5} \int_{\substack{t_{f}\left(k_{\mathrm{p}}\right) \\ 0, i_{\mathrm{p}}}}^{t_{\left.f, i_{\mathrm{p}}\right)}^{\left(k_{\mathrm{p}}\right.}}\left(\frac{\alpha_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}}{\alpha_{\text {max }}}\right)^{2}+\left(\frac{\beta_{\mathrm{p}_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}}{\beta_{\max }}\right)^{2} \mathrm{~d} t, \\ & \left(i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}}\right) \end{align*} $ | (16) |
于是np发制导炮弹的协同目标函数可以表示为
| $ \begin{equation*} J_{\text {col }}=\sum\limits_{i_{\mathrm{p}}=1}^{n_{\mathrm{p}}} J_{i_{\mathrm{p}}} \end{equation*} $ | (17) |
设多阶段最优控制问题包含P个阶段,性能函数可以写为
| $ \begin{align*} J= & \sum\limits_{p=1}^{P}\left[\boldsymbol{\Phi}^{(p)}\left(\boldsymbol{x}_{0}^{(p)}, t_{0}^{(p)}, \boldsymbol{x}_{\mathrm{f}}^{(p)}, \boldsymbol{t}_{\mathrm{f}}^{(p)}, \boldsymbol{s}\right)+\right. \\ & \left.\int_{t_{0}^{(p)}}^{t_{\mathrm{f}}^{(p)}} \Gamma\left(\boldsymbol{x}^{(p)}(t), \boldsymbol{u}^{(p)}(t), t, \boldsymbol{s}\right) \mathrm{d} t\right] \end{align*} $ | (18) |
式中:s为静态参数向量,Φ(·)为端点值性能函数,Γ(·)为积分型性能指标待积分函数,(·)(p)为P阶段最优控制问题第p∈ 1, 2, …, P阶段的变量。
需要注意的是,伪谱法中最优控制问题的第p阶段与弹道规划模型第kp阶段并不一定是一一对应的关系。弹道规划模型的第kp阶段对应制导炮弹飞行过程的每个阶段,是物理客观而不可随意改变的。然而,伪谱法中最优控制问题的第p阶段是数学意义上的,数学意义上的第p阶段可以包含多个物理对象,例如在第p阶段内联立np发制导炮弹的约束,并且其顺序也可以变换,因为序列二次规划问题中改变约束函数的先后顺序并不影响最终优化结果。
动态函数约束为
| $ \begin{equation*} \dot{\boldsymbol{x}}^{(p)}=\boldsymbol{f}\left(\boldsymbol{x}^{(p)}, \boldsymbol{u}^{(p)}, t^{(p)}, \boldsymbol{s}\right), (p=1, \cdots, P) \end{equation*} $ | (19) |
不等式路径约束为
| $ \begin{gather*} \boldsymbol{C}_{\min }^{(p)} \leqslant \boldsymbol{C}^{(p)}\left(\boldsymbol{x}^{(p)}, \boldsymbol{u}^{(p)}, t^{(p)}, \boldsymbol{s}\right) \leqslant \boldsymbol{C}_{\max }^{(p)} \\ (p=1, \cdots, P) \end{gather*} $ | (20) |
以及连续性约束为
| $ \begin{gather*} \boldsymbol{L}\left(\boldsymbol{x}^{(p)}\left(t_{\mathrm{f}}^{(p)}\right), t_{\mathrm{f}}^{(p)} ; \boldsymbol{x}^{(p+1)}\left(t_{0}^{(p+1)}\right), t_{0}^{(p+1)}\right)=\mathbf{0} \\ (p=1, \cdots, P-1) \end{gather*} $ | (21) |
于是式(18)~(21)构成多阶段最优控制问题POCP。POCP可简写为
| $ P_{\text {OCP }}: \\ \min J_{\text {OCP }}\\ {\rm{s}}{\rm{. t}}{\rm{. }}~~ \boldsymbol{h}_{\text {OCPC }}=\left[\boldsymbol{h}_{\text {OCP }}^{(1)}, \cdots, \boldsymbol{h}_{0 \mathrm{CP}}^{(p)}, \cdots, \boldsymbol{h}_{\mathrm{OCP}}^{(P)}\right]^{\mathrm{T}} \leqslant \mathbf{0} $ | (22) |
式中:JOCP为标准最优控制问题的目标函数,hOCP(p)为P阶段最优控制问题第p阶段的约束函数向量,hOCPC为约束函数向量集合。
2.2 多阶段最优控制问题伪谱离散针对多阶段最优控制问题(optimal control problem,OCP)的每一阶段,Radau伪谱法(Radau pseudo-spectral method,RPM)将状态变量和控制变量分别离散到一系列勒让德-高斯-拉道(Legendre-Gauss-Radau,LGR) 节点上,并以经过这些节点的拉格朗日插值多项式近似状态变量和控制变量,从而将连续的无限维的OCP转化为有限维的非线性规划问题(nonlinear programming problem,NLP)。LGR节点是非对称、非等间距的,采用它的根作为插值节点可以有效避免等距高阶多项式插值经常出现的龙格现象[25]。相比Gauss伪谱法,RPM不需附加的积分约束,转换得到的NLP更为简洁[26]。
RPM的伪谱时间τ∈[-1, 1]与第p阶段物理时间t(p)∈[t0(p), tf(p)]的映射关系为
| $ \begin{equation*} t^{(p)}=\frac{t_{\mathrm{f}}^{(p)}-t_{0}^{(p)}}{2} \tau+\frac{t_{f}^{(p)}+t_{0}^{(p)}}{2}, (p=1, \cdots, P) \end{equation*} $ | (23) |
状态变量和控制变量可由拉格朗日多项式近似表示为:
| $\boldsymbol{x}^{(p)}(\boldsymbol{\tau}) \approx \boldsymbol{X}^{(p)}(\boldsymbol{\tau})=\sum\limits_{i=0}^{N(p)} \boldsymbol{X}_{i}^{(p)} L_{i}(\boldsymbol{\tau}) $ | (24) |
| $ \boldsymbol{u}^{(p)}(\boldsymbol{\tau}) \approx \boldsymbol{U}^{(p)}(\boldsymbol{\tau})=\sum\limits_{i=0}^{N(p)-1} \boldsymbol{U}_{i}^{(p)} L_{i}(\boldsymbol{\tau}) $ | (25) |
其中:Li为第i个节点对应的拉格朗日多项式函数的基函数,可写作:
| $ \begin{gathered} L_{i}(\tau)=\prod\limits_{h=0, h \neq i}^{N^{(p)}} \frac{\tau-\tau_{h}}{\tau_{i}-\tau_{h}} \\ \left(i=0, 1, \cdots, N^{(p)} ; p=1, \cdots, P\right) \end{gathered} $ |
式中:N(p)为第p阶段配置点数目,Xi(p)、Ui(p)分别为第p阶段第i个节点的状态变量和控制变量。
对状态变量插值多项式(24)两端关于伪谱时间τ求导可得
| $ \begin{equation*} \frac{\mathrm{d} \boldsymbol{X}^{(p)}}{\mathrm{d} \boldsymbol{\tau}}=\sum\limits_{i=0}^{N(p)} \boldsymbol{X}_{i}^{(p)} \frac{\mathrm{d} L_{i}(\boldsymbol{\tau})}{\mathrm{d} \boldsymbol{\tau}}, (p=1, \cdots, P) \end{equation*} $ | (26) |
进一步可以得到:
| $ \begin{gather*} \boldsymbol{X}^{(p)} D=\frac{t_{\mathrm{f}}^{(p)}-t_{0}^{(p)}}{2} \boldsymbol{f}^{(p)}\left(\boldsymbol{X}^{(p)}, \boldsymbol{U}^{(p)}, t_{0}^{(p)}, t_{\mathrm{f}}^{(p)}\right), \\ (p=1, \cdots, P) \end{gather*} $ | (27) |
式中:
RPM路径约束的离散形式为
| $ \begin{gather*} \boldsymbol{C}_{\min }^{(p)} \leqslant \boldsymbol{C}^{(p)}\left(\boldsymbol{X}_{i}^{(p)}, \boldsymbol{U}_{i}^{(p)}, \tau_{i}, t_{0}^{(p)}, t_{\mathrm{f}}^{(p)}\right) \leqslant \boldsymbol{C}_{\max }^{(p)}, \\ \left(p=1, \cdots, P ; i=0, \cdots, N^{(p)}\right) \end{gather*} $ | (28) |
相似地,离散化的连续性约束为
| $ \begin{gather*} L_{\mathrm{c}}\left(\boldsymbol{X}_{N(p)}^{(p)}, t_{\mathrm{f}}^{(p)} ; \boldsymbol{X}_{0}^{(p+1)}, t_{0}^{(p+1)}\right)=\mathbf{0}, \\ (p=1, \cdots, P-1) \end{gather*} $ | (29) |
由数值分析理论[27]可知,目标函数的离散形式为
| $ \begin{align*} J= & \sum\limits_{p=1}^{p} \Phi^{(p)}\left(\boldsymbol{X}_{0}^{(p)}, t_{0}^{(p)}, \boldsymbol{X}_{N(p)}^{(p)}, \boldsymbol{t}_{\mathrm{f}}^{(p)}, \boldsymbol{S}\right)+ \\ & \sum\limits_{p=1}^{p} \frac{t_{\mathrm{f}}^{(p)}-t_{0}^{(p)}}{2} \sum\limits_{a=0}^{N(p)-1} \omega_{a}^{(p)} \boldsymbol{\varphi}_{a}^{(p)} \end{align*} $ | (30) |
式中:φa(p)为第p阶段被积函数在第a个配置点的值, ωa(p)为对应配置点的积分权系数。
于是无限维的多阶段最优控制问题POCP被转化为有限维非线性规划问题PNLP,PNLP可简写为
| $ P_{\mathrm{NLP}}:\\ \left\{\begin{array}{l} \min J_{\text {NLP }} \\ \text { s. t. } \boldsymbol{h}_{\text {NLPG }}=\left[\boldsymbol{h}_{\text {NLP }}^{(1)}, \cdots, \boldsymbol{h}_{\text {NLP }}^{(p)}, \cdots, \boldsymbol{h}_{\text {NLP }}^{(p)}\right]^{\mathrm{T}} \leqslant \mathbf{0} \end{array}\right. $ | (31) |
式中:
标准化后的非线性规划问题PNLP可采用序列二次规划求解器SNOPT求解。
3 协同弹道规划算法 3.1 单阶段弹道规划问题描述由多阶段最优控制问题与多阶段弹道规划模型的论述可知,制导炮弹的第kp阶段并不一定和最优控制问题的第p阶段对应,具体关系需要根据算法所采用的架构确定。
为方便后续对算法的描述,在这里先简化单阶段弹道规划问题的描述。设
| $ \begin{align*} & P_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}: \\ & \left\{\begin{array}{l} \min J_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)} \\ \text { s.t. } \boldsymbol{f}_{\left.\mathrm{c}, \mathrm{i}_{\mathrm{p}}\right)}^{\left(k_{\mathrm{p}}\right)} \leqslant \mathbf{0} \end{array}\right. \end{align*} $ | (32) |
协同弹道规划算法按照求解时是否分开求解各自弹道可分为分布式和集中式架构,对应的弹道规划算法分别为分布式协同弹道规划算法(D-CTPM)和传统集中式协同弹道规划算法(TC-CTPM),本文分析两种算法的不足,提出一种增广集中式协同弹道规划算法(AC-CTPM)。
图 3为D-CTPM算法流程示意图,图 4为TC-CTPM算法和本文所提AC-CTPM算法流程示意图。接下来将详细介绍3种算法并分析两种传统方法的缺点以及本文所提方法的优点。

|
图 3 分布式算法架构 Fig. 3 Distributed algorithm architecture |

|
图 4 集中式算法架构 Fig. 4 Centralized algorithm architecture |
如图 3所示,D-CTPM算法可描述为一个3层式结构,分别为飞行时间预测层、协同时间获取层和协同轨迹输出层[20]。在D-CTPM算法的每一层,每一发制导炮弹的方案弹道都单独规划,第ip发制导炮弹的弹道规划问题以多阶段最优控制问题的形式可以表示为
| $ \begin{aligned} & \min J_{\text {OCP }}=\sum\limits_{k_{\mathrm{p}}=1}^{5} J_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)} \\ \text { s. t. } & \boldsymbol{h}_{\mathrm{OCPC}}=\left[\boldsymbol{h}_{\mathrm{OCP}}^{(1)} \boldsymbol{h}_{\mathrm{OCP}}^{(2)} \boldsymbol{h}_{\mathrm{OCP}}^{(3)} \boldsymbol{h}_{\mathrm{OCP}}^{(4)} \boldsymbol{h}_{\mathrm{OCP}}^{(5)}\right]^{\mathrm{T}} \leqslant \mathbf{0} \\ & \boldsymbol{h}_{\mathrm{OCP}}^{(p)}=\boldsymbol{f}_{\mathrm{c}, i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)}, \left(p=k_{\mathrm{p}}=1, \cdots, 5\right) \\ & \boldsymbol{L}_{i_{\mathrm{p}}}=\mathbf{0} \end{aligned} $ | (33) |
式中:Lip为第ip发制导炮弹的连续性约束函数向量。可以看出,第ip发制导炮弹的5个阶段弹道规划问题可以由第ip发制导炮弹的5个阶段的弹道优化问题按序组合,最后增加连续性约束即可构成5个阶段最优控制问题。参考文献[4],分布式算法的协同时间常采用预测时间的平均值,即
| $ \begin{equation*} t^{*}=\frac{\sum\limits_{i_{\mathrm{p}}=1}^{n_{\mathrm{p}}} t_{\mathrm{f}, i_{\mathrm{p}}}^{(5)}}{n_{\mathrm{p}}} \end{equation*} $ | (34) |
如图 4左半流程图所示,TC-CTPM算法在一个阶段内联立所有制导炮弹的动态方程[19],np发制导炮弹的5个阶段弹道规划问题联立后成为一个5个阶段协同弹道规划问题,通过一次求解获得协同方案弹道。采用TC-CTPM算法,np发制导炮弹协同弹道规划问题按照最优控制问题的形式可写作:
| $\begin{aligned} & \min J_{\text {OCP }}=J_{\text {col }}=\sum_{i_r=1}^{n_{\mathrm{n}}} \sum_{k_{\mathrm{r}}=1}^5 J_{i_p}^{\left(k_p\right)} \\ & \text { s. t. } \boldsymbol{h}_{\mathrm{OCPC}}=\left[\boldsymbol{h}_{\mathrm{OCP}}^{(1)}, \cdots, \boldsymbol{h}_{\mathrm{OCP}}^{(p)}, \cdots, \boldsymbol{h}_{\mathrm{OCP}}^{(5)}\right]^{\mathrm{T}} \leqslant \mathbf{0} \\ & \boldsymbol{h}_{\mathrm{OCP}}^{(p)}=\left[\boldsymbol{f}_{\mathrm{c}, 1}^{(p)}, \cdots, \boldsymbol{f}_{\mathrm{c}, i_i}^{(p)}, \cdots, \boldsymbol{f}_{\mathrm{c}, n_{\mathrm{p}}}^{(p)}\right]^{\mathrm{T}},(p=1, \cdots, 5) \\ & \boldsymbol{L}_{i_{\mathrm{p}}}=\mathbf{0},\left(i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}}\right) \\ & \end{aligned} $ | (35) |
TC-CTPM算法的协同时间为第5阶段终止时间,即
| $ t^*=t_{\mathrm{f}}^{(5)} $ | (36) |
由式(34)可知,D-CTPM的协同时间是通过平均值法求得,该协同时间不是通过优化迭代获取,难以保证是最优协同攻击时间。
TC-CTPM算法是在伪谱法的每一阶段内联立多发制导炮弹的动态方程,建模方式和求解单发制导炮弹的多阶段弹道规划问题相似,只是增加了伪谱法每一阶段内的变量和约束,这种处理方式简单且容易理解。该算法在求解单阶段且同时发射同时弹着弹道规划问题时效果较好,但规划5个阶段的滑翔增程制导炮弹协同方案弹道时会存在不足,这是因为传统集中式协同算法架构默认包含了np发制导炮弹各阶段初末时间等式约束,即
| $ \left\{\begin{array}{l} t_{0, 1}^{\left(k_{\mathrm{p}}\right)}=t_{0, 2}^{\left(k_{\mathrm{p}}\right)}=\cdots=t_{0, n_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)} \\ t_{\mathrm{f}, 1}^{\left(k_{\mathrm{p}}\right)}=t_{\mathrm{f}, 2}^{\left(k_{\mathrm{p}}\right)}=\cdots=t_{\mathrm{f}, n_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)} \end{array}, \left(k_{\mathrm{p}}=1, \cdots, 5\right)\right. $ | (37) |
显然这些约束对于制导炮弹协同弹道规划问题来说属于冗余约束,可以预见,这些冗余的时间约束会影响协同方案弹道的协同性能指标。此处,冗余的初末时间等式约束导致传统TC-CTPM算法对作战任务场景适用性降低,其只能求解同时发射同时弹着弹道规划问题,无法求解如按序列时间发射或序列时间弹着等非同时发射以及非同时弹着弹道规划问题。
为了克服分布式算法和传统集中式算法的上述缺点,本文提出一种增广集中式协同弹道规划算法(AC-CTPM),其算法流程如图 4的右半图所示。
采用AC-CTPM算法,np发制导炮弹协同弹道规划问题按照最优控制问题的形式可写作:
| $ \begin{align*} \min & J_{\text {OCP }}=J_{\text {col }}=\sum\limits_{i_{\mathrm{p}}=1}^{n_{\mathrm{p}}} \sum\limits_{k_{\mathrm{p}}=1}^{5} J_{i_{\mathrm{p}}}^{\left(k_{\mathrm{p}}\right)} \\ \text { s.t. } & \boldsymbol{h}_{\text {OCP }}=\left[\boldsymbol{h}_{\text {OCP }}^{(1)}, \cdots, \boldsymbol{h}_{\text {OCP }}^{(p)}, \cdots, \boldsymbol{h}_{\text {OCP }}^{\left(5 n_{\mathrm{p}}\right)}\right]^{\mathrm{T}} \leqslant \mathbf{0} \\ & \boldsymbol{h}_{\text {OCP }}^{(p)}=\boldsymbol{f}_{\left.c, \mathrm{c}, \mathrm{p}_{\mathrm{p}}\right)}^{\left(\mathrm{p}_{\mathrm{p}}\right.}, \\ & \left(k_{\mathrm{p}}=1, \cdots, 5 ; i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}} ; p=k_{\mathrm{p}}+5\left(i_{p}-1\right)\right) \\ & \boldsymbol{L}_{i_{\mathrm{p}}}=\mathbf{0}, \left(i_{\mathrm{p}}=1, \cdots, n_{\mathrm{p}}\right) \end{align*} $ | (38) |
可以看出AC-CTPM算法中,最优控制问题一个阶段内仅包含一发制导炮弹的一个阶段,np发制导炮弹协同弹道规划问题被扩展成一个5np阶段最优控制问题。增广集中式算法的协同时间为
| $ \begin{equation*} t^{*}=t_{\mathrm{f}}^{(p)}, \left(p=5, 10, \cdots, 5 n_{\mathrm{p}}\right) \end{equation*} $ | (39) |
本文提出的AC-CTPM算法可以令协同攻击时间为Radau伪谱法中的一个静态变量,即令s=[t*],从而通过优化获得协同攻击时间。理论上,AC-CTPM算法通过最优化获得的协同时间比D-CTPM算法采用求平均值获得的协同时间更理想。相比传统TC-CTPM算法,本文提出的AC-CTPM算法为每一发制导炮弹的每一飞行阶段都分配了初末时间变量,时间约束可按照任务场景的需求设置,理论上可处理制导炮弹能力范围内的任意时间序列发射任意时间序列弹着的协同弹道规划问题,自然也包括传统TC-CTPM算法能求解的问题范围,从集合的角度上来说,传统TC-CTPM算法能解决的问题为本文所提AC-CTPM算法一个子集。
3.2.4 协同弹道规划问题初始预测值获取算法集中式算法架构建立的协同攻击弹道规划问题变量数量庞大,问题复杂度较高,较差的初始预测值可能导致问题求解困难,求解耗时长,甚至出现求解失败的情况。为提高本文AC-CTPM算法的求解效率,本文提出一种初始预测值获取算法,为协同弹道规划问题提供更理想的初始预测值。该初始预测值获取算法作为AC-CTPM算法的一部分,初始值获取耗时计入AC-CTPM算法对整个协同弹道规划问题的求解耗时。
采用伪谱法可以快速有效地规划出简化的2D方案弹道,从变分学角度来看,该2D方案弹道就在3D协同方案弹道的邻域内,求解器只需要对2D方案弹道做较少的调整就能快速收敛到最优化的3D协同方案弹道。由于每发制导炮弹方案弹道的初始预测弹道获取方式相似,这里仅讨论一发制导炮弹初始预测弹道获取方法。
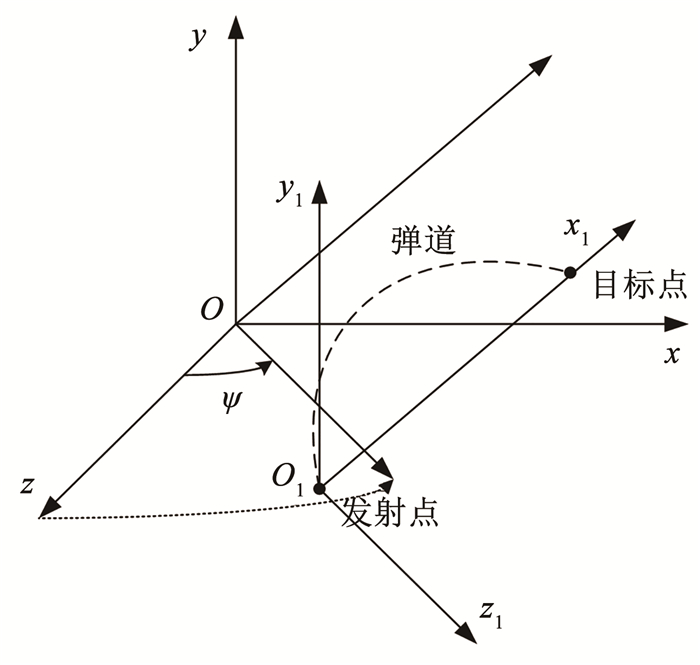
首先根据每发制导炮弹发射点位置和目标点位置,建立一个新的地面坐标系O1-x1y1z1,其中O1位于炮弹发射点,O1-x1轴为弹道面和水平面的交线,O1-y1竖直向上,O1-z1轴由右手定则确定。在弹道面O1-x1y1内快速规划出2D方案弹道,然后将2D方案弹道扩展成3D方案弹道并转换回原地面坐标系中O-xyz。
由式(1)、(2)可以看出,在O1-x1y1面内中规划初始预测方案弹道相比在原3D地面坐标系中可以减少两个状态变量ψv和z以及一个控制变量β,问题变量减少了1/3,这可以极大减少问题求解耗时。
新地面坐标系O1-x1y1z1可以看作是由原地面坐标系O-xyz绕O-y轴旋转ψ,然后平移得到,如图 5所示。
|
图 5 坐标转换示意 Fig. 5 Coordinate conversion diagram |
初始时刻弹目距离为
| $\begin{equation*} R_{\mathrm{p} 00}=\sqrt{\left(x_{\mathrm{t}}-x_{0}\right)^{2}+\left(z_{\mathrm{t}}-z_{0}\right)^{2}} \end{equation*} $ | (40) |
在新地面坐标系中,制导炮弹位于新坐标系原点(0, 0, 0),目标坐标为(Rpt0, 0, 0)。
新地面坐标系是在原地面坐标系基础上增加下标“1”,同理,原弹道规划模型各标量增加下标“1”表示新坐标系下弹道规划模型,于是可以假设,在新坐标系中规划得到的2D方案弹道为
| $\left\{\begin{array}{l} \boldsymbol{x}_{1}=\left[\begin{array}{lllll} v_{1} & \theta_{1} & x_{1} & y_{1} & m_{1} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{u}_{1}=\alpha_{1} \end{array}\right. $ | (41) |
在新地面坐标系O1-x1y1z1中,2D方案弹道扩展为3D方案弹道为
| $ \left\{\begin{array}{l} \boldsymbol{x}_{1}=\left[\begin{array}{lllllll} v_{1} & \theta_{1} & \psi_{\mathrm{v} 1} & x_{1} & y_{1} & z_{1} & m_{1} \end{array}\right]^{\mathrm{T}} \\ \boldsymbol{u}_{1}=\left[\begin{array}{ll} \alpha_{1} & \beta_{1} \end{array}\right]^{\mathrm{T}} \\ \psi_{\mathrm{v} 1}=0 \\ z_{1}=0 \\ \beta_{1}=0 \end{array}\right. $ | (42) |
原地面坐标系到新地面坐标系的转换关系为
| $ \left[\begin{array}{l} x_{1} \\ y_{1} \\ z_{1} \end{array}\right]=\left[\begin{array}{ccc} \cos \psi & 0 &-\sin \psi \\ 0 & 1 & 0 \\ \sin \psi & 0 & \cos \psi \end{array}\right]\left[\begin{array}{l} x \\ y \\ z \end{array}\right]-\left[\begin{array}{l} x_{0} \\ y_{0} \\ z_{0} \end{array}\right] $ | (43) |
反之,新地面坐标系到原地面坐标系的转换关系为
| $ \left[\begin{array}{l} x \\ y \\ z \end{array}\right]=\left[\begin{array}{ccc} \cos \psi & 0 & \sin \psi \\ 0 & 1 & 0 \\ -\sin \psi & 0 & \cos \psi \end{array}\right]\left[\begin{array}{l} x_{1} \\ y_{1} \\ z_{1} \end{array}\right]+\left[\begin{array}{l} x_{0} \\ y_{0} \\ z_{0} \end{array}\right] $ | (44) |
假设初始位置和目标都在水平地面上,则y0=0。所以新坐标系到原坐标系的转换关系可以简化为
| $ \left\{\begin{array}{l} x=x_{1} \cos \psi+x_{0} \\ y=y_{1} \\ z=-x_{1} \sin \psi+z_{0} \end{array}\right. $ | (45) |
新坐标系相对原坐标系旋转了一个方位角ψ,于是新坐标系中的2D方案弹道映射到原坐标系中时的弹道偏角为一个恒定值,即
| $ \begin{equation*} \psi_{v} \equiv \psi \end{equation*} $ | (46) |
很显然,地面坐标系绕O-y轴的旋转不会改变弹道倾角,即
| $ \begin{equation*} \theta=\theta_{1} \end{equation*} $ | (47) |
地面坐标系的旋转和平移也不会影响制导炮弹的动力学变量,即
| $\left\{\begin{array}{l} v=v_{1} \\ m=m_{1} \\ \alpha=\alpha_{1} \\ \beta=\beta_{1} \end{array}\right. $ | (48) |
综上所述,在新地面坐标系中规划的2D方案弹道转换到原地面坐标系扩展成3D初始预测弹道的转换关系式(42)、式(45)~式(48)。
4 仿真和分析本文以某火箭助推滑翔增程制导炮弹为仿真对象。首先采用本文所提AC-CTPM算法对单炮多发同时弹着协同弹道规划问题进行求解,以验证其有效性。然后分别采用本文所提AC-CTPM算法,传统的D-CTPM算法和TC-CTPM算法对多炮单发制导炮弹同时弹着协同弹道规划问题进行求解,对3种算法的仿真结果进行对比分析,以验证本文所提AC-CTPM算法的优越性。
4.1 仿真参数设置滑翔制导炮弹出炮口初速为800m/s;气动参数由风洞吹风试验获得;大气模型采用美国1976标准大气模型;令θfU=-30°,vfL=200 m/s,助推火箭工作时长为14.068 s。其他参数见表 1~3。仿真采用一台搭载英特尔i7-8700k@ 3.7 GHz处理器的计算机,仿真软件为matlab。
| 表 1 制导炮弹参数 Tab. 1 Parameters of guided projectile |
| 表 2 弹道变量的上、下边界 Tab. 2 Upper and lower bounds of ballistic variables |
| 表 3 各阶段持续时长的上、下边界 Tab. 3 Upper and lower bounds of the duration of each phase |
本文仿真场景为一门炮按照一定时间序列依次发射5发制导炮弹按照指定方位角同时弹着攻击(50 km, 0, 0)处的目标,具体仿真参数见表 4。
| 表 4 单炮多发制导炮弹协同仿真参数 Tab. 4 Simulation parameters of cooperative single-gun multiple-firing |
|
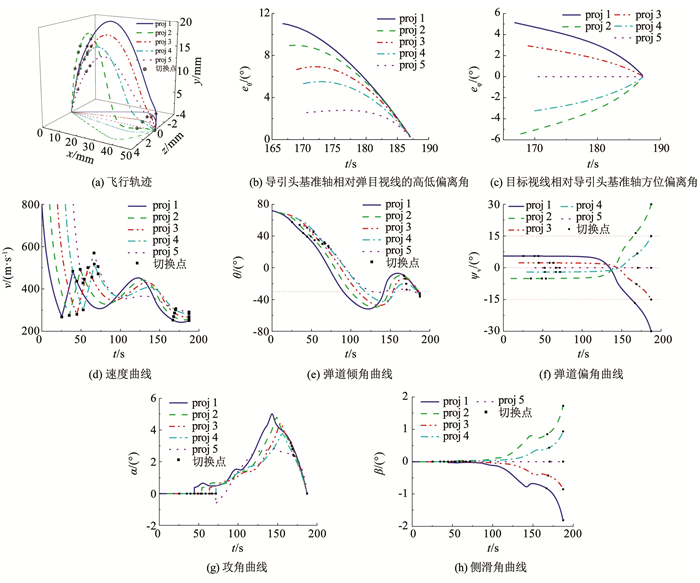
图 6 单炮多发制导炮弹同时弹着优化结果 Fig. 6 Optimization results of single-gun multiple-firing hit simultaneously |
| 表 5 最优化末制导起始点 Tab. 5 Optimal starting point of terminal guidance phase |
| 表 6 射角最优解 Tab. 6 Optimal solution of firing angle (°) |
| 表 7 时间节点最优解 Tab. 7 Optimal solution of time nodes |
由图 6(a)、(e)、(f)、(g)、(h)可知,制导炮弹的前3个飞行阶段为无控段,依次间隔10 s发射的5发制导炮弹在不同的纵向面内飞行,直至滑翔段起始点。控制舵开启后,制导炮弹产生攻角和侧滑角,从而产生纵向控制力和侧向控制力,调整制导炮弹的弹道,最终以预定的攻击方位角同时命中目标。
由图 6(a)、(e)、(g)和表 6、7可知,依次间隔10 s发射的5发制导炮弹,所需飞行时间越长的制导炮弹发射角越大,获得的射高也更高,这是由于较大的射角可以将动能转换为重力势能,更高的射高也有利于延长制导炮弹下降过程中的飞行时间。由图 6(a)、(f)、(h)和表 6、7可知,依次间隔10 s发射的5发制导炮弹以不同的方位角发射,越早发射的制导炮弹发射方位角的绝对值越大,这是由于在合理范围内,偏离弹道面的发射方位角越大,制导炮弹侧向运动距离越大,越有利于获得更大的飞行时间。
由图 6(d)可知,制导炮弹的速度在出炮口后的第1阶段速度快速减小,在第2阶段速度又快速增大这是由于制导炮弹在第1阶段刚出炮口,制导炮弹速度较大,气动阻力较大,此外还有部分动能转换为重力势能,造成第1阶段速度快速减小,而在第2飞行阶段,助推火箭点火提供轴向推力,使制导炮弹的速度快速增大。
由图 6(b)、(c)可知,在末制导段,5发制导炮弹的弹目连线相对导引头基准轴在高低和方位两个方向的偏差角都小于导引头视场角,满足导引头视场角约束。由表 5可知,5发制导炮弹末制导起始点与目标的距离RMT和导引头最大探测距离Rs相等,满足本文建立的末制导起始点约束。由图 6(d)、(e)可知,这一组制导炮弹的末速度都大于200 m/s,末弹道倾角小于-30°,满足预先规定的末速度和末弹道倾角约束。此外,由图 6(g)、(h)可知,作为控制量的攻角和侧滑角满足其上、下界限约束。
综上所述,本文所提AC-CTPM算法规划的协同方案弹道,依次间隔10 s发射的5发制导炮弹以预定的攻击方位角同时命中目标,实现了预定的协同攻击方式,证明了本文所提AC-CTPM算法的有效性。
4.3 算例2:多炮单发制导炮弹协同攻击一个目标为验证本文所提AC-CTPM算法的优越性,本文分别采用AC-CTPM算法和传统D-CTPM算法以及传统TC-CTPM算法进行仿真对比分析。由于传统TC-CTPM算法受时间节点等式约束的限制,只能规划同时发射同时弹着弹道规划问题,所以本文针对的任务场景为从不同位置的多门炮对同一地点的静止目标进行同时发射同时弹着协同攻击,具体仿真参数见表 8。
| 表 8 多炮单发制导炮弹协同仿真参数 Tab. 8 Cooperative simulation parameters of multiple-gun single-firing |
分别选取表 8中前2发、前3发、前4发以及全部5发制导炮弹仿真参数进行仿真。仿真结果如图 7、8和表 9~12所示(由于弹道模型和任务场景相同,3种算法规划的方案弹道相似度较高,考虑文章篇幅,仅展示5发制导炮弹任务场景下的协同方案弹道,且传统D-CTPM算法以及传统TC-CTPM算法仅展示飞行轨迹)。图 7为3种算法规划的3D协同飞行轨迹,其中O-xz平面内的曲线为飞行轨迹的俯视图。图 8为AC-CTPM算法规划的协同飞行参数。表 9~表 11为3种算法优化出的最优化时间节点。表 12为分别采用3种算法规划协同方案弹道得到的协同目标函数值以及对问题的求解耗时。

|
图 7 协同飞行轨迹 Fig. 7 Cooperative flight trajectory |

|
图 8 AC-CTPM同时弹着优化结果 Fig. 8 Optimization results for simultaneous impact by AC-CTPM |
| 表 9 D-CTPM时间节点最优解 Tab. 9 Optimal solution of time nodes by D-CTPM |
| 表 10 TC-CTPM时间节点最优解 Tab. 10 Optimal solution of time nodes by TC-CTPM |
| 表 11 AC-CTPM时间节点最优解 Tab. 11 Optimal solution of time nodes by AC-CTPM |
| 表 12 目标函数值和问题求解耗时 Tab. 12 Target function value and problem solving time |
由图 7和表 9~表 11可知,3种算法均实现了算例2预定的多炮单发制导炮弹协同攻击。对比可以发现,3种算法规划的飞行轨迹相似度较高,这是由于3种算法针对同样的算例场景且采用同一制导炮弹模型。由图 8可知,发射平台在发射前调整方位角对准了目标,每发制导炮弹发射后全程弹道偏角固定不变,侧滑角都保持为零,这有利于实现控制能量最优。在滑翔段和末制导段仅提供攻角控制量,调整制导炮弹飞行轨迹,使其在满足约束条件的前提下完成协同攻击任务。
由表 9~表 11可知,传统TC-CTPM算法规划的方案弹道,每发制导炮弹各阶段切换时间相同,而传统D-CTPM算法和本文所提AC-CTPM算法规划的方案弹道各阶段切换时间不同。这是由于传统TC-CTPM算法在Radau伪谱法的每一阶段内联立多发制导炮弹的弹道模型,即每发制导炮弹共用了初末时间变量,因此每发制导炮弹的各阶段切换时间点必定相等,而传统TC-CTPM算法和本文所提AC-CTPM算法中Radau伪谱法的每一阶段仅包含一发制导炮弹的一个飞行阶段,没有多发制导炮弹共用初末时间变量的情况,因此,除了飞行终止时间相同外,这两种算法优化的切换时间点各制导炮弹都不同。
由表 12可知,传统D-CTPM算法规划4发制导炮弹算例的目标函数明显偏离正常值。经检验发现,由D-CTPM算法协同时间计算式(34)确定的4发制导炮弹协同飞行时间为143.662 s,然而分别规划4发制导炮弹的最短飞行时间方案弹道可知,第3发制导炮弹的最短飞行时间为149.229 s,即第3发制导炮弹无法满足协同时间约束,所以传统D-CTPM算法规划的4发制导炮弹协同方案弹道无效。然而,AC-CTPM算法不存在异常值,这说明本文所提AC-CTPM算法的普适性比传统D-CTPM算法强。
分别采用3种算法规划协同方案弹道,随着协同攻击炮弹数目的增加,协同目标函数增大。随着问题复杂度增加,问题求解耗时遵循增大的趋势。值得注意的是,表 12中D-CTPM算法规划2发制导炮弹算例的求解耗时却比3发制导炮弹的算例求解耗时多,AC-CTPM算法规划4发制导炮弹算例的求解耗时却比3发制导炮弹的算例求解耗时少,这是由于问题求解耗时不仅受问题复杂度影响,还与求解器迭代收敛路径有关。
由表 12可知,AC-CTPM算法相比于传统TC- CTPM算法,目标函数平均减小5.07%;相比D-CTPM算法,目标函数值减小32.98%。并且,本文所提AC-CTPM算法相比传统TC-CTPM算法,问题求解耗时减少86.48%;相比D-CTPM算法,问题求解耗时减少82.36%。即,相比传统TC-CTPM算法和D-CTPM算法,本文所提AC-CTPM算法以更低的时间成本求得了更优的性能指标,即规划出了更理想的方案弹道,这验证了本文所提AC-CTPM算法的优越性。
5 结论1) 本文所提AC-CTPM算法规划的协同方案弹道满足制导炮弹自身性能约束以及协同任务约束,验证了AC-CTPM算法的有效性。
2) 传统TC-CTPM算法仅能求解同时发射同时攻击弹道规划问题,而AC-CTPM算法发射时间和攻击时间可自由指定,即本文所提AC-CTPM算法对任务场景普适性比传统TC-CTPM算法强。
3) 相比传统D-CTPM算法,AC-CTPM算法的协同时间变量不是固定值,这导致AC-CTPM算法的任务场景普适性比传统D-CTPM算法强。
4) 采用本文所提AC-CTPM算法规划的协同方案弹道,相比传统TC-CTPM算法,目标函数值平均减小5.07%;相比传统D-CTPM算法目标函数值减小32.98%。
5) 本文所提AC-CTPM算法相比传统TC-CTPM算法,问题求解耗时减少86.48%;相比传统D-CTPM算法,问题求解耗时减少82.36%。
6) 综上所述,本文所提AC-CTPM算法任务场景普适性强,其规划的协同方案弹道相比传统TC-CTPM算法和传统D-CTPM算法,性能指标更好,规划耗时更短,验证了本文所提算法的有效性和优越性。此外,本文所提AC-CTPM算法成功地将制导炮弹协同弹道规划问题的求解耗时降低到50 s之内,理论上,由matlab代码改用计算效率更高的C语言,问题求解耗时将进一步大幅下降,这对实战中进行工程应用具有一定现实意义。
| [1] |
LIU Chaoyue, ZHANG Cheng, XIONG Fenfen. Multistage cooperative trajectory planning for multimissile formation via Bi-level sequential convex programming[J]. IEEE Access, 2020, 8: 22834. DOI:10.1109/ACCESS.2020.2967873 |
| [2] |
赵建博, 杨树兴. 多导弹协同制导研究综述[J]. 航空学报, 2017, 38(1): 020256. ZHAO Jianbo, YANG Shuxing. Review of multi-missile cooperative guidance[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(1): 020256. DOI:10.7527/S1000-6893.2016.0136 |
| [3] |
张达, 刘克新, 李国飞. 多约束条件下的协同制导研究进展[J]. 南京信息工程大学学报(自然科学版), 2020, 12(5): 530. ZHANG Da, LIU Kexin, LI Guofei. Recent advances of cooperative guidance under multiple constraints[J]. Journal of Nanjing University of Information Science & Technology (Natural Science Edition), 2020, 12(5): 530. DOI:10.13878/j.cnki.jnuist.2020.05.002 |
| [4] |
JIANG Huan, AN Ze, YU Ya'nan, et al. Cooperative guidance with multiple constraints using convex optimization[J]. Aerospace Science and Technology, 2018, 79: 426. DOI:10.1016/j.ast.2018.06.001 |
| [5] |
WANG Yijing, TAO Hong, SONG Tao, et al. Cooperative guidance for speed-varying vehicle against moving target[C]// 2022 13th Asian Control Conference (ASCC). Jeju: IEEE, 2022: 1788. DOI: 10.23919/ASCC56756.2022.9828326
|
| [6] |
黄国强, 陆宇平, 南英. 飞行器轨迹优化数值算法综述[J]. 中国科学: 技术科学, 2012, 42(9): 1016. HUANG Guoqiang, LU Yuping, NAN Ying. A survey of numerical algorithms for trajectory optimization of flight vehicles[J]. Scientia Sinica (Technologica), 2012, 42(9): 1016. DOI:10.1007/s11431-012-4946-y |
| [7] |
史金光, 王中原, 孙洪辉, 等. 制导炮弹滑翔弹道优化设计方法研究[J]. 南京理工大学学报, 2011, 35(5): 610. SHI Jinguang, WANG Zhongyuan, SUN Honghui, et al. Optimization design method for glide trajectory of guided projectiles[J]. Journal of Nanjing University of Science and Technology, 2011, 35(5): 610. DOI:10.14177/j.cnki.32-1397n.2011.05.022 |
| [8] |
孙瑞胜, 薛晓中, 沈坚平. 一种乘波外形导弹增程段弹道的最优控制解法[J]. 弹道学报, 2008, 20(4): 57. SUN Ruisheng, XUE Xiaozhong, SHEN Jianping. Trajectory optimization for a hypersonic waverider missile in extended range period by means of optimal control[J]. Journal of Ballistics, 2008, 20(4): 57. |
| [9] |
郭铁丁. 深空探测小推力轨迹优化的间接法与伪谱法研究[D]. 北京: 清华大学, 2012 GUO Tieding. Study of indirect and pseudospectral methods for low thrust trajectory optimization in deep space exploration[D]. Beijing: Tsinghua University, 2012 |
| [10] |
王丽英, 张友安, 黄诘. 带约束的末制导律与伪谱法轨迹优化[M]. 北京: 国防工业出版社, 2015. WANG Liying, ZHANG Youan, HUANG Jie. Constrained terminal guidance law and pseudospectral trajectory optimization[M]. Beijing: National Defense Industry Press, 2015. |
| [11] |
胡朝江, 陈士橹. 改进直接多重打靶算法及其应用[J]. 飞行力学, 2004, 22(1): 14. HU Chaojiang, CHEN Shilu. An improved multiple shooting algorithm for direction solution of optimal control problem and its application[J]. Flight Dynamics, 2004, 22(1): 14. DOI:10.3969/j.issn.1002-0853.2004.01.004 |
| [12] |
SUBCHAN S S. A direct multiple shooting method for missile trajectory optimization with the terminal bunt manoeuvre[J]. IPTEK: The Journal for Technology and Science, 2011, 22(3): 147. DOI:10.12962/j20882033.v22i3.67 |
| [13] |
陈琦, 王中原, 常思江. 基于Gauss伪谱法的滑翔弹道快速优化[J]. 弹道学报, 2014, 26(2): 17. CHEN Qi, WANG Zhongyuan, CHANG Sijiang. Rapid optimization of gliding trajectory based onGauss pseudospectral method[J]. Journal of Ballistics, 2014, 26(2): 17. DOI:10.3969/j.issn.1004-499X.2014.02.004 |
| [14] |
徐秋坪. 滑翔制导炮弹弹道规划及其自抗扰控制系统研究[D]. 南京: 南京理工大学, 2018 XU Qiuping. Trajectory optimization and active-disturbance-rejection control system for gliding guided projectiles[D]. Nanjing: Nanjing University of Science and Technology, 2018 |
| [15] |
LIU Suyun, LI Shuai, LIU Yiji, et al. Research on anti-ship missile cooperative trajectory planning based on Gauss pseudospectral method[C]//Proceedings of 2021 5th Chinese Conference on Swarm Intelligence and Cooperative Control. Singapore: Springer, 2023: 1163. DOI: 10.1007/978-981-19-3998-3_111
|
| [16] |
GU Xueqiang, SHEN Lincheng, CHEN Jing, et al. A virtual motion camouflage approach for cooperative trajectory planning of multiple UCAVs[J]. Mathematical Problems in Engineering, 2014, 2014: 748974. DOI:10.1155/2014/748974 |
| [17] |
ZHAO Zhe, YANG Jian, NIU Yifeng, et al. A hierarchical cooperative mission planning mechanism for multiple unmanned aerial vehicles[J]. Electronics, 2019, 8(4): 443. DOI:10.3390/electronics8040443 |
| [18] |
许强强, 葛健全, 杨涛, 等. 面向突防的多导弹协同弹道规划方法[J]. 中国惯性技术学报, 2018, 26(4): 524. XU Qiangqiang, GE Jianquan, YANG Tao, et al. Cooperative trajectory planning for penetration of multiplemissiles[J]. Journal of Chinese Inertial Technology, 2018, 26(4): 524. DOI:10.13695/j.cnki.12-1222/o3.2018.04.018 |
| [19] |
刘超越, 张成. 基于分布式并行伪谱-神经网络算法的双脉冲导弹多阶段协同轨迹优化[J]. 兵工学报, 2020, 41(10): 1988. LIU Chaoyue, ZHANG Cheng. Multi-stage cooperative trajectory optimization of dual-pulse missile based on decentralized parallel Pseudospectral-neural network algorithm[J]. Acta Armamentarii, 2020, 41(10): 1988. DOI:10.3969/j.issn.1000-1093.2020.10.008 |
| [20] |
李征, 彭博, 陈海东, 等. 可重复使用航天器时间协同飞行轨迹优化[J]. 计算机仿真, 2020, 37(1): 40. LI Zheng, PENG Bo, CHEN Haidong, et al. Time-coordination reentry trajectory design for reusable launch vehicle[J]. Computer Simulation, 2020, 37(1): 40. DOI:10.3969/j.issn.1006-9348.2020.01.010 |
| [21] |
钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学[M]. 北京: 北京理工大学出版社, 2000. QIAN Xingfang, LIN Ruixiong, ZHAO Yanan. Missile flight mechanics[M]. Beijing: Beijing Institute of Technology Press, 2000. |
| [22] |
MA Shuai, WANG Xugang, WANG Zhongyuan, et al. Consensus-based finite-time cooperative guidance with field-of-view constraint[J]. International Journal of Aeronautical and Space Sciences, 2022, 23(5): 966. DOI:10.1007/s42405-022-00473-4 |
| [23] |
MUKHERJEE D, KUMAR S R. Field-of-view constrained impact time guidance against stationary targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2021, 57(5): 3296. DOI:10.1109/TAES.2021.3074202 |
| [24] |
ZHANG Youan, WANG Xingliang, WU Huali. Impact time control guidance law with field of view constraint[J]. Aerospace Science and Technology, 2014, 39: 361. DOI:10.1016/j.ast.2014.10.002 |
| [25] |
李庆扬, 王能超, 易大义. 数值分析[M]. 5版. 北京: 清华大学出版社, 2008. LI Qingyang, WANG Nengchao, YI Dayi. Numerical analysis[M]. 5th ed. Beijing: Tsinghua University Press, 2008. |
| [26] |
GARG D, PATTERSON M A, FRANCOLIN C, et al. Direct trajectory optimization and costate estimation off inite-horizon and infinite-horizon optimal control problems using a Radau pseudospectral method[J]. Computational Optimization and Applications, 2011, 49(2): 335. DOI:10.1007/s10589-009-9291-0 |
| [27] |
RAY S S. Numerical analysis with algorithms and programming[M]. Florida: CRC Press, 2018.
|
 2024, Vol. 56
2024, Vol. 56


