2. 工业流体节能与污染控制教育部重点实验室(青岛理工大学),山东 青岛 266520
2. Key Laboratory of Industrial Fluid Energy Conservation and Pollution Control(Qingdao University of Technology), Ministry of Education, Qingdao 266520, Shandong, China
旋转机械辐射噪声一直是环境污染的重要来源。这类噪声因旋转发声、流体与固体相互作用、声辐射机理复杂、声波在运动媒介中传播、声场特性及传播模式易耦合,难解析。旋转声场的声辐射预估一直都是声学领域的重要研究课题和热点问题,备受学者们关注。
早在1952年,Lighthill[1]针对旋转声辐射问题,提出了声学类比法用于预估空气动力学噪声,开启了旋转声辐射的研究大门。随后Lowson等[2]、Prieur等[3]、Brentner等[4]、Kessler等[5]、居鸿宾等[6]在时域内开展了旋转声辐射模型的研究。因辐射模型涉及变量多、时间依赖性强、解析难,局限了实际应用,为此,吴九汇等[7]、Mao等[8]、刘志红等[9-11]在时域声辐射基础上,通过傅里叶变换和旋转声源的几何结构特点,构建了旋转点源的声辐射频域解析表达式,且数值分析了声场特征。宋正旋等[12]更为详细讨论了马赫数对旋转点源声场特征的影响。Poletti等[13-14]和Carley[15]推导了球坐标和柱坐标系下的旋转点源声压表达式,用于预估螺旋桨的辐射声场,更有学者将其应用在航空叶轮机[16]及扬声器[17]的辐射声场研究。为进一步提高声场预估精度,文献[18-19]给出影响旋转声源声场的关键函数贝塞尔函数的球谐展开及特性,给出谐波阶次截断的方法,可有效提高旋转声源声辐射的精确度。该理论也可应用于旋转点源和偶极子源的声成像[20]及声源定位[21]。这些研究大多针对自由空间声辐射,而实际的旋转声场多在有限区域内,很多情况下,旋转源在管道[22]和壳体[23-24]中,忽略这种有界约束,单纯由自由场旋转源的声辐射进行预估,大大降低了预估的准确性和实用性,为此,利用有限元法[25-26]或边界积分法[27],结合数值分析方法研究管道内旋转声辐射。文献[28]引入覆盖整个旋转源区的固定克希荷夫曲面,并将边界元方法应用于固定克希荷夫曲面,利用克希荷夫曲面将叶轮噪声源与边界元连接起来,有效预测了离心叶轮非定常流场和声场,但其关键变量旋转声压的法向导数取值困难,声辐射特征不明确,限制其推广应用。
基于此,本文提出利用克希荷夫积分方法预估旋转声场,在旋转点源声辐射基础上,推导了横向及纵向偶极子频域声压解析表达式,采用克希荷夫积分融合点源和偶极子源,构建了克希荷夫源及其声辐射预估模型,将声辐射预估由传统的点源声场叠加转换为面源的声辐射计算,进一步数值分析了辐射声场特性,探求了旋转频率、声源基频和声源尺度对声场的影响,给出一种用于预估旋转声辐射的新的频域解析方法。
1 克希荷夫旋转声场预估方法 1.1 旋转声源的声压表达式基于旋转点源的声辐射,构建旋转横向、纵向偶极子声源及其辐射声压频域表达式。如图 1(a)所示,在x-y旋转平面内,横向偶极子置于周向,绕z轴旋转,在空气动力性噪声研究中,该项表示载荷源;如图 1(b)所示,纵向偶极子置于z轴方向,它表示厚度源。图 1中,偶极子源点坐标为(r0, θ0, φ0),观察点坐标(rs, θs, φs),rs为观察点空间位置矢量,rs= |rs|,r0为偶极子源的半径矢量,r0= |r0|,θ0、θs为俯仰角,φ0、φs为方位角,从旋转轴z起顺时针方向为正向,β为rs与r0之间夹角,R为观察点至偶极子源的距离,d为两相位相反点源间距。

|
图 1 偶极子源的旋转运动示意 Fig. 1 Schematic diagram of rotational motion of dipole source |
由旋转点源声辐射可知,其辐射声压频域表达式为
| $ p_0=\frac{1}{2 \mathtt{π}} \int_{-\infty}^{\infty} Q(\tau) \mathrm{e}^{\mathrm{i} \omega \tau} \mathrm{d} \tau G_{\mathrm{r}}=A_0 G_{\mathrm{r}} $ | (1) |
式中:A0为点源强度;
自由空间中格林函数Gr的展开式为
| $ \frac{\mathrm{e}^{\mathrm{i} k R}}{4 \mathtt{π} R}=\mathrm{i} k \sum\limits_{n=0}^{\infty}(-1)^{\mathrm{n}}(2 n+1) j_{\mathrm{n}}\left(k r_{<}\right) h_{\mathrm{n}}\left(k r_{>}\right) P_{\mathrm{n}}(\cos \beta) $ | (2) |
在单位强度简谐源条件下,由球贝塞尔函数、勒让德函数和旋转几何关系,将式(2)代入式(1),得出声压解析式为
| $ p_0=\sum\limits_{n=0}^{\infty} \frac{\mathrm{i} k(2 n+1)}{4 \mathtt{π}} B_{\mathrm{n}}\left\{P_{\mathrm{n}}(0) P_{\mathrm{n}}\left(\cos \theta_s\right)+C_{\mathrm{n}} D_{\mathrm{m}}\right\} $ | (3) |
其中:
| $ \begin{aligned} B_{\mathrm{n}}= & \left\{\begin{array}{l} j_{\mathrm{n}}\left(k r_{\mathrm{s}}\right) h_{\mathrm{n}}\left(k r_0\right), r_0>r_{\mathrm{s}} \\ j_{\mathrm{n}}\left(k r_0\right) h_{\mathrm{n}}\left(k r_{\mathrm{s}}\right), r_0<r_{\mathrm{s}} \end{array}\right. \\ C_{\mathrm{n}}= & \sum\limits_{m=1}^n \frac{(n-m)!}{(n+m)!} P_n^m(0) P_n^m\left(\cos \theta_{\mathrm{s}}\right) \\ D_{\mathrm{m}}= & {\left[\mathrm{e}^{\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)} \delta\left(\omega+m \omega_{\mathrm{R}}-\omega_0\right)+\right.} \\ & \left.\mathrm{e}^{-\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)} \delta\left(\omega-m \omega_{\mathrm{R}}-\omega_0\right)\right] \end{aligned} $ |
式中: Bn为球贝塞尔函数,Cn为相关勒让德函数,r< 、r>分别为r0、rs中较小者和较大者,m为声场谐波阶次(取自然数),ω0为声源角频率,ωR为声源旋转角频率,ω为声辐射角频率。
1.1.2 横向偶极子声压通过对式(2)的空间位置微分变换,推导出横向和纵向偶极子的格林函数表达式,将解析格林函数代入式(1),可得出相应横向和纵向偶极子的声压解析式。
横向偶极子的格林函数为Gφ,Gφ是通过对旋转格林函数Gr在方位角φ上的微分可得
| $ \begin{aligned} G_{\mathrm{r}}= & -\frac{1}{r_{\mathrm{s}}} \frac{\partial G_{\mathrm{r}}}{\partial \varphi}= \\ & \sum\limits_{n=0}^{\infty} \frac{-\mathrm{i} k(2 n+1)}{4 \mathtt{π} r_{\mathrm{s}}} B_{\mathrm{n}}\left\{P_{\mathrm{n}}(0) P_{\mathrm{n}}\left(\cos \theta_{\mathrm{s}}\right)-\right. \\ & \left.\mathrm{i} m C_{\mathrm{n}}\left(\mathrm{e}^{\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}+\mathrm{e}^{-\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}\right)\right\} \end{aligned} $ | (4) |
式(4)代入式(1),得出横向偶极子声压解析表达式为
| $ \begin{aligned} p_y(x, \omega)= & \sum\limits_{n=0}^{\infty} \frac{-\mathrm{i} k(2 n+1)}{4 \mathtt{π} r_{\mathrm{s}}} B_{\mathrm{n}}\left\{P_{\mathrm{n}}(0) P_{\mathrm{n}}\left(\cos \theta_{\mathrm{s}}\right)-\right. \\ & \left.\mathrm{i} m C_{\mathrm{n}} D_{\mathrm{m}}\right\} \end{aligned} $ | (5) |
纵向偶极子的格林函数为Gz,Gz是对旋转格林函数Gr在旋转轴z向的微分为
| $ \begin{aligned} G_{\mathrm{z}}= & -\frac{\partial G_{\mathrm{r}}}{\partial z}= \\ & \frac{-\mathrm{i} k(2 n+1)}{4 \mathtt{π} r_{\mathrm{s}} \sin \theta_{\mathrm{s}}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}} C_{\mathrm{n}}^{\prime}\left(\mathrm{e}^{\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}+\mathrm{e}^{-\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}\right)- \\ & \frac{\mathrm{i} k(2 n+1)}{4 \mathtt{π}} \cos \theta_{\mathrm{s}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}}^{\prime} C_{\mathrm{n}}\left(\mathrm{e}^{\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}+\mathrm{e}^{-\mathrm{i} m\left(\varphi_{\mathrm{s}}-\varphi_0\right)}\right) \end{aligned} $ | (6) |
其中球贝塞尔函数和相关勒让德函数有下列导数性质:
| $ \begin{aligned} B_{\mathrm{n}}^{\prime} & =\left\{\begin{array}{l} j_{\mathrm{n}}\left(k r_{\mathrm{s}}\right) h_{\mathrm{n}}^{\prime}\left(k r_0\right), r_0>r_{\mathrm{s}} \\ j_{\mathrm{n}}^{\prime}\left(k r_0\right) h_{\mathrm{n}}\left(k r_{\mathrm{s}}\right), r_0<r_{\mathrm{s}} \end{array}\right. \\ C_{\mathrm{n}}^{\prime} & =\sum\limits_{m=1}^n \frac{(n-m)!}{(n+m)!} P_n^m(0) P_n^{\prime m}\left(\cos \theta_{\mathrm{s}}\right) \end{aligned} $ |
式(6)代入式(1),可得出纵向偶极子声压解析表达式为
| $ \begin{aligned} p_{\mathrm{z}}(x, \omega)= & \frac{-\mathrm{i} k(2 n+1)}{4 \mathtt{π}}\left[\frac{\sum\limits_{n=0}^{\infty} B_{\mathrm{n}} m C_{\mathrm{n}} D_{\mathrm{m}}}{r_{\mathrm{s}} \sin \theta_{\mathrm{s}}}+\right. \\ & \left.\cos \theta_{\mathrm{s}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}}^{\prime} C_{\mathrm{n}} D_{\mathrm{m}}\right] \end{aligned} $ | (7) |
运用克希荷夫积分方法研究旋转声场的声辐射,将旋转源的声辐射视为一个包围在其外部的克希荷夫面源的声辐射。依据上述旋转点源及偶极子源声辐射和克希荷夫积分公式,取球面为克希荷夫源建立面,将包围在内部的旋转声源的声特征转换到克希荷夫源面上,形成新的面源即克希荷夫源;由旋转点源、横、纵偶极子源声压及其法向导数,利用克希荷夫积分法,推导出克希荷夫面源的声辐射模型及其声压解析式。
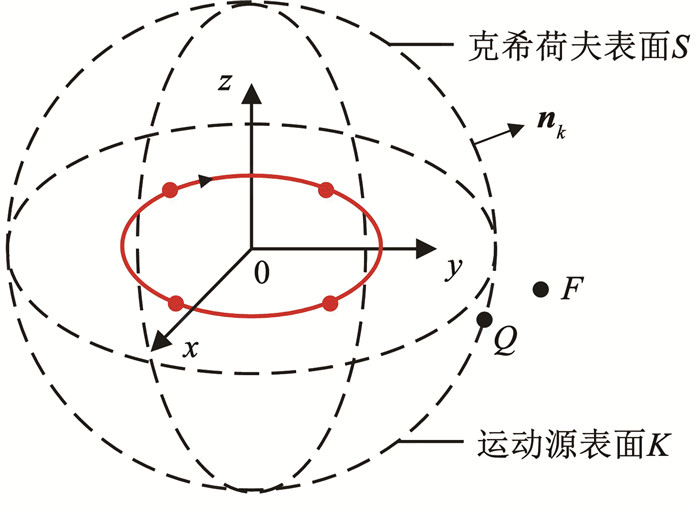
1.2.1 克希荷夫源克希荷夫面可以为任意曲面,为简化计算,选球面为克希荷夫面,构建克希荷夫源。如图 2所示。图 2中K为旋转声源表面,S为包围旋转声源的克希荷夫面,Q为S面上的任意点,F为S面外的任意空间一点,nk为克希荷夫表面的法向矢量。
|
图 2 克希荷夫源示意 Fig. 2 Schematic diagram of Kirchhoff source |
克希荷夫积分是一种求解声波动方程的积分解法,以封闭曲面为边界,限定求解区域,通过设置声源函数和边界条件及其声源相对边界的位置,进行边界内部及外部区域的声辐射计算。其具体形式为
| $ p_F=\frac{1}{4 \mathtt{π}}\left[\iint\limits_{\mathrm{S}} p_0 \frac{\partial G_{\mathrm{r}}}{\partial n_{\mathrm{s}}}-\frac{\partial p_0}{\partial n_{\mathrm{s}}} G_{\mathrm{r}}\right] \mathrm{d} S $ | (8) |
式中: pF为边界S外任意点的声压,F∉S;p0为点源声压;∂p0/∂ns为偶极子源的势函数;Gr、∂Gr/∂ns分别为自由空间的格林函数及其法向导数。
本文利用式(8)推导克希荷夫源的声辐射。探讨旋转声源的旋转速度小于声速的情况,即旋转马赫数Ma < 1,由式(8)可知,Gr、∂Gr/∂ns、p0及∂p0/∂ns是进行克希荷夫源声辐射计算的4个关键参量。Gr为旋转格林函数,如式(2),p0为旋转点源的辐射声压,如式(3)沿球面S的格林函数Gr的法向导数表示为
| $ \frac{\partial G_{\mathrm{r}}}{\partial n_{\mathrm{s}}}=\frac{\partial G_{\mathrm{r}}}{\partial R_{\mathrm{s}}} \frac{\partial R_{\mathrm{s}}}{\partial n_{\mathrm{s}}}=-\left(\mathrm{i} k+\frac{1}{R_{\mathrm{s}}}\right) G_{\mathrm{r}} \frac{\partial R_{\mathrm{s}}}{\partial n_{\mathrm{s}}} $ | (9) |
式中Rs为球形半径。
∂p0/∂ns为偶极子源的声压,即
| $ \begin{aligned} \frac{\partial p_0}{\partial n_{\mathrm{s}}} & =\left(p_{\mathrm{z}}+p_{\mathrm{y}}\right)= \\ & \quad \frac{-\mathrm{i} k(2 n+1)}{4 \mathtt{π}}\left[\frac{\sin \theta_{\mathrm{s}}+1}{r_{\mathrm{s}} \sin \theta_{\mathrm{s}}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}} m C_{\mathrm{n}} D_{\mathrm{m}}+\right. \\ & \left.\quad \cos \theta_{\mathrm{s}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}}^{\prime} C_{\mathrm{n}} D_{\mathrm{m}}\right] \end{aligned} $ | (10) |
将式(2)、(3)、(9)、(10)代入式(8),得到克希荷夫旋转声场声压频域模型为
| $ p_{\mathrm{F}}=\frac{k^2(2 n+1)^2}{4 \mathtt{π}} U(\mathrm{i} k V-W) $ | (11) |
其中:
| $ \begin{aligned} & U=\sum\limits_{n=0}^{\infty}(-1)^n B_{\mathrm{n}} P_{\mathrm{n}}(\cos \beta) \\ & V=\sum\limits_{n=0}^{\infty} B_{\mathrm{n}}\left\{P_{\mathrm{n}}(0) P_{\mathrm{n}}\left(\cos \theta_{\mathrm{s}}\right)+C_{\mathrm{n}} D_{\mathrm{m}}\right\} \\ & W=\left[\frac{\sum\limits_{n=0}^{\infty} B_{\mathrm{n}}^{\prime} m C_{\mathrm{n}} D_{\mathrm{n}}}{r_{\mathrm{s}}^2 \sin \theta_{\mathrm{s}}}-\cos \theta_{\mathrm{s}} \sum\limits_{n=0}^{\infty} B_{\mathrm{n}}^{\prime \prime} C_{\mathrm{n}} D_{\mathrm{n}}\right] \end{aligned} $ |
由式(11)可知,克希荷夫旋转声辐射的声压解析式中,因n∈[0, ∞],m∈[1, n],谐波阶次n,m直接影响声辐射解析精度,n和m取值太小,计算精度低;取值太大,解析计算量增加,有效的谐波阶次截断和合理的门限值是进行式(11)解析的关键。
经大量数值计算和统计分析,得出影响谐波阶次截断的关键因素为旋转声辐射角频率ω和旋转马赫数Ma。由式(3)可知,旋转声辐射角频率ω=ω0+mωR;相应波数表示为km=k0+mkR,旋转马赫数Ma=ωRr0/c0=kRr0。当谐波阶次m取正值时,声辐射角频率ω>ω0,则m>(ω-ω0)/ωR,即m> (km-k0)/kR;m取负值时,ω < ω0,则m < (ω-ω0)/ωR,即m < (km-k0)/kR。由球贝塞尔函数的特性,要求n>kmr0,此时,n可表示为m的函数:
| $ n(m)=\max \left\{\left[\left|k_0+m k_{\mathrm{R}}\right| r_0\right], |m|\right\} $ | (12) |
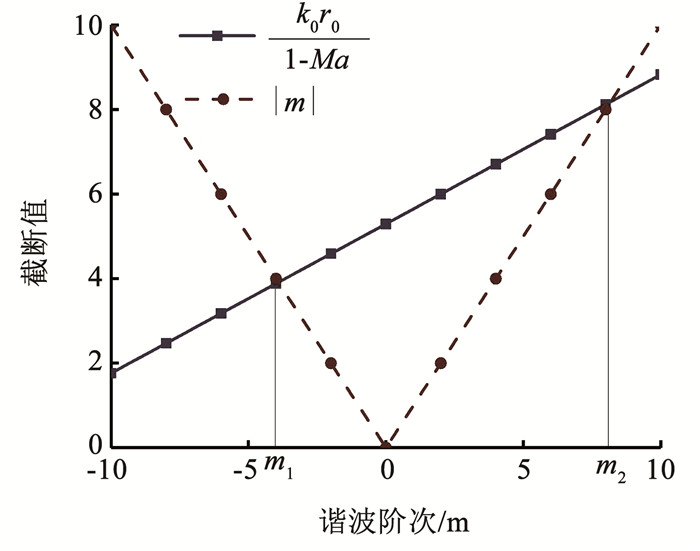
由式(12)可知,谐波阶次n的取值与谐波阶次m,波数k0、kR及旋转半径r0有关,其关系如图 3、4所示。当Ma < 1,谐波阶次n截断的门限值范围[m1, m2]为:
| $ \begin{aligned} & m_1=\frac{-k_0 r_0}{1+k_{\mathrm{R}} r_0}=\frac{-k_0 r_0}{1+M} \\ & m_2=\frac{k_0 r_0}{1-k_{\mathrm{R}} r_0}=\frac{k_0 r_0}{1-M} \end{aligned} $ | (13) |
|
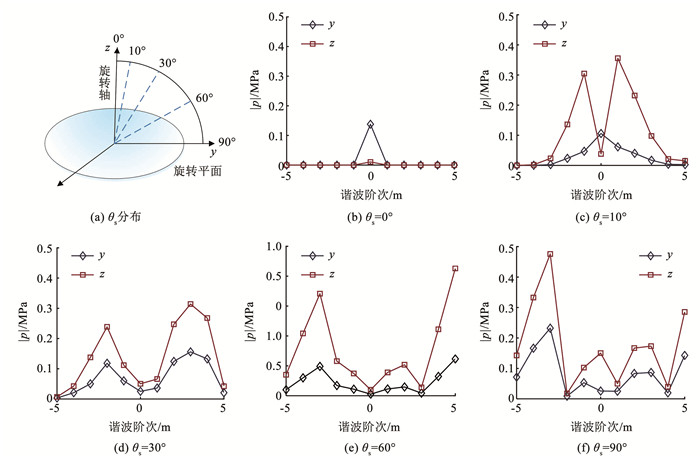
图 3 不同观察点的横向y和纵向z的声压分布图 Fig. 3 Transverse and longitudinal sound pressure distribution at different observation points |

|
图 4 马赫数与谐波阶次的关系 Fig. 4 Relationship between Mach number and harmonic order |
为验证克希荷夫声辐射预估方法有效性,从偶极子源贡献、谐波阶次截断、声场等价性和声场特性方面开展数值仿真分析。仿真数据中旋转半径r0=0.3 m,观察半径rs=2.0 m,基频ω0=6 800 rad/s,旋转频率ωR=500 rad/s,源方位角φ0=0°,俯仰角θ0为90°,观察点方位角φs=-45°,因旋转声辐射具有空间对称性,俯仰角θs取0°、10°、30°、60°、90°,如图 3(a)所示,谐波阶次m∈[-5, 5]。
图 3(b)为两者沿旋转轴方向的声辐射,辐射声场频率都只有基频,没有调制谐波,声压值横向大于纵向;图 3(f)为旋转平面上的声辐射,声场频率谐波阶次变丰富,增加数量一致,声压值纵向大于横向;进一步比较图 3(c)~3(e),随θs角度增大,声场频率谐波阶次增加,增加的谐波阶次数量一致,纵向声压值是横向值的3~4倍。
由此,式(10)中
为验证谐波阶次截断及门限值的有效性,进行了阶次截断和截断误差的分析。
由式(13)可知,当给定k0和r0时,m1和m2随Ma∈(0, 1)的变化曲线如图 4所示。
当给定Ma时,m1和m2与k0r0(r0 < rs)成正比的变化曲线如图 5所示。
|
图 5 波数与谐波阶次的关系 Fig. 5 Relationship between wave number and harmonic order |
由此,由式(12)可知截断值取最大,可准确得出任意条件下谐波n和m的截断及其门限值。
为说明截断有效性,定义截断误差评价参数ε,它为多个观察点处,不同n,m,由式(11)计算得出的声压的空间平均相对误差:
| $ \varepsilon=\sum\limits_{i=1}^N \frac{1}{N} \frac{\left\|p_i^{(m)}(x, \omega)-p_i^{(m-1)}(x, \omega)\right\|}{\left\|p_i^{(m)}(x, \omega)\right\|} \times 100 \% $ | (14) |
由仿真结果可知,根据截断值的不同取值所得到的声压分布几乎相同,如图 6所示。说明谐波阶次取值大于10时,对辐射声压没有显著影响,其相对误差在0.1%以内,符合相对误差小于0.001。

|
图 6 谐波阶次变化下的声压分布 Fig. 6 Sound pressure distribution under harmonic order changes |
为进一步验证式(11)克希荷夫声辐射模型的有效性,进行旋转源等价性分析。设单位幅值的旋转点源置于图 2,旋转半径0.3 m,外部包裹0.5 m半径的克希荷夫球面,观察点距离球面1.5 m,在给定基频ω0、旋转角频率ωR, 谐波阶次n,m,由式(1)和式(11)分别计算并给出俯仰角θs在10°、30°、60°、90° 4个观察点处的声压,同时计算两者绝对误差,其等价性分析如图 7所示。

|
图 7 等价性比较 Fig. 7 Equivalence comparison |
由图 7及大量计算统计得出,在旋转声场中,利用克希荷夫积分法构建的克希荷夫面源声辐射模型与旋转源模型沿观察角的声压分布相对误差在5%左右,表明等价性良好,验证了克希荷夫声辐射模型的有效性。
2.4 旋转声场特性旋转声场与其他运动声场一样,也具有显著的多普勒效应和指向性特征。旋转声场的多普勒效应体现在频移和幅值变化两方面。由式(3)可知,旋转声场频率被旋转频率谐波调制,即ω=ω0±mωR,换言之,声场辐射频率与声源频率不一致,叠加了旋转频率,空间频率分布具有间断特点;其声压幅值的变化与基频ω0、旋转马赫数及旋转半径r0有关。其影响分别如图 8~10所示。
|
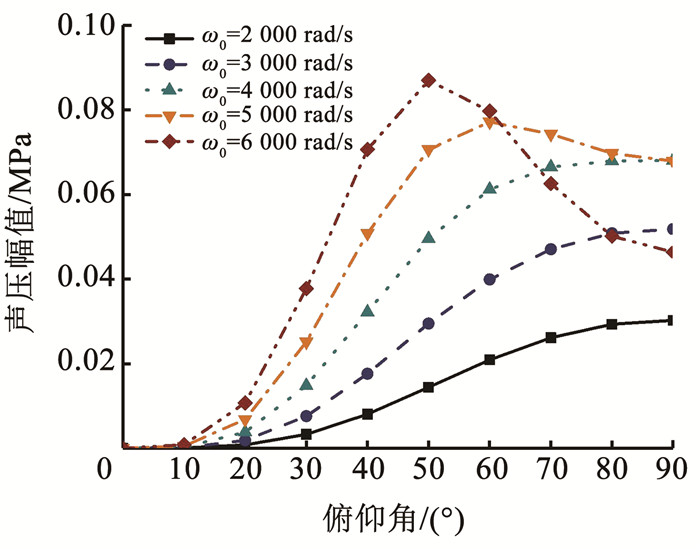
图 8 基频变化下的声压分布图 Fig. 8 Sound pressure distribution with changing fundamental frequency |
|
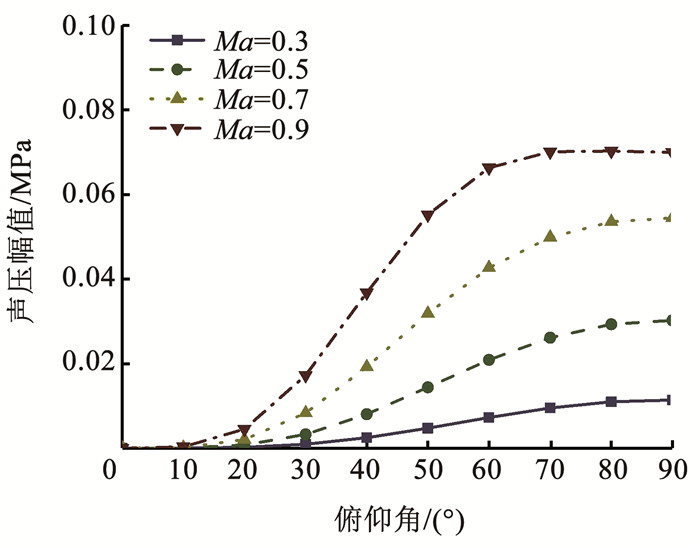
图 9 马赫数变化下的声压分布图 Fig. 9 Sound pressure distribution with changing Mach number |
|
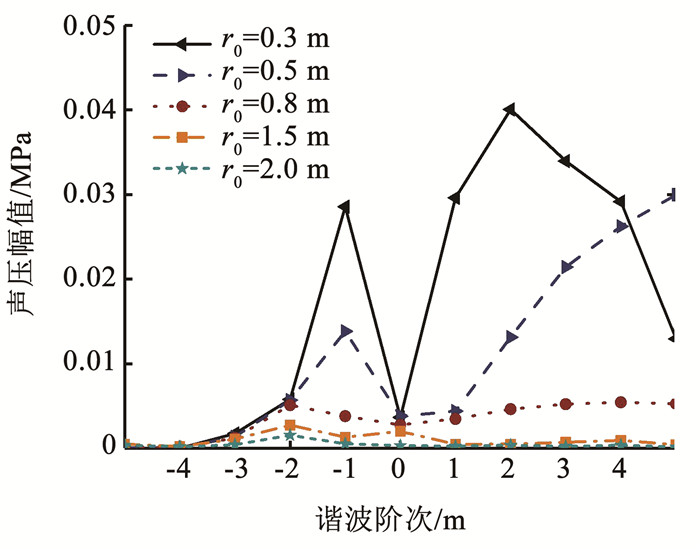
图 10 旋转半径变化下的声压分布图 Fig. 10 Sound pressure distribution with changing rotation radius |
图 8为给定旋转半径r0=0.3 m及Ma=0.5情况下,辐射声压沿俯仰角随基频的变化。由图 8可知,基频越大,相应的声压幅值越大,其中,俯仰角在40°~60°之间,声压幅值最大。在基频超过5 000 rad/s且俯仰角>50°时,声压幅值出现下降趋势,在基频为6 000 rad/s时,辐射声压下降更为明显。
图 9为给定基频ω0=6 800 rad/s及旋转半径r0=0.3 m,辐射声压沿俯仰角随马赫数的变化。由图 9可知,声压幅值随马赫数增大而增大,声压沿俯仰角方向增大,在90°方向,辐射声压达到最大。
图 10为给定基频ω0=6 800 rad/s和Ma=0.5,辐射声压随旋转半径r0的变化。由图 10可知,随着旋转半径的增大,声压幅值显著减小;当旋转半径r0=0.3 m时,声压幅值最大,且具有明显的跳跃性和间断性,谐波也越尖锐;当旋转半径r0=2.0 m时,辐射声压几乎为零。
数值分析方位角φs对辐射声场的影响,分别取φs为0°、30°、90°、180°、270°时的声压幅值变化,如图 11所示。

|
图 11 方位角变化下的声压分布图 Fig. 11 Sound pressure distribution with changing azimuth |
由仿真结果可知,观察位置的方位角变化对克希荷夫源声压幅值及谐波分量影响不明显,对辐射声压空间分布的影响可以忽略。
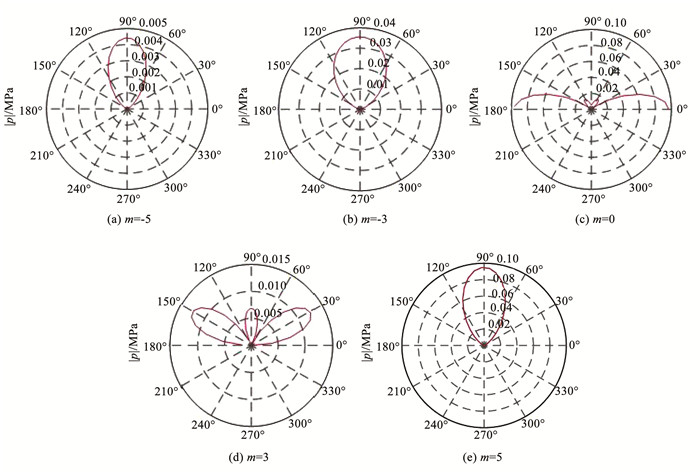
旋转声场具有显著的指向性特征,如图 12给出了不同谐波阶次的声场指向性。
|
图 12 指向性 Fig. 12 Directionality |
仿真结果表明,声压分布更多集中在旋转平面θs=90°附近且声场具有强烈的指向性。如图 12(a)、12(b)所示,当谐波阶次m=-5、m=-3时,声压显著增大,但指向性仍然突出;在谐波阶次m=0时(如图 12(c)所示),表示声场频率只有基频,声压分布集中在旋转轴θs=0°方向,声压最大;当m=3时(如图 12(d)所示),谐波变多,分散在30°~90°左右,声压幅值较大;如图 12(e)所示,m=5时,谐波集中在旋转平面θs=90°附近。
3 实验验证为进一步验证克希荷夫源的有效性,以麦克风作为理论中的观察点,搭建并列式线性麦克风阵列展开实验研究。
3.1 麦克风阵列结构参数线性麦克风的主要结构参数:刚性支架长度1 m,下端固定支撑,10个麦克风,麦克风间距0.01 m,均匀间距分布。测试范围为80~1 000 Hz,麦克风灵敏度为8.40~10.92 mV/Pa。
3.2 实验室研究为验证上述理论与数值分析的旋转声场特性,在半消声室内进行了旋转叶片风扇噪声测试。测试对象为三叶风扇,转速最大1 430 r/min。由于风扇作业时,气流沿旋转叶片平面流动,风压随距离衰减。因此,为避免风扇气流脉动冲击对麦克风的测试产生影响以及风扇外部壳体对声场的散射影响,拆除外部罩壳,突出旋转叶片,风扇配装防风罩。实验设备采用LMS Test. Lab声学平台系统,测试现场如图 13所示。

|
图 13 麦克风阵列与叶片位置关系 Fig. 13 Relationship between microphone array and blade position |
为验证数值仿真的准确性,分别测试叶片在轴向(俯仰角为0°)与旋转平面方向(俯仰角为90°)的声压频谱特性,测试结果如图 14(a)、14(b)所示;俯仰角为30°、60°时,声场声压分布,测试结果如图 14(c)、14(d)所示;不同转速下声场的分布特性,测试结果如图 14(e)、14(f)所示。

|
图 14 声场特性频谱图 Fig. 14 Spectrum diagram of sound field characteristics |
数字0, 1, 2, 3分别为谐波阶次,其中0为基频。
综合图 14的声场测试结果,得出以下结论:1)在旋转轴方向,旋转声场基频突出,在旋转平面方向,声场谐波丰富,指向性明显,这与仿真结果一致。2)转速越大,旋转声场的谐波越丰富,即旋转马赫数的变化对旋转声场的影响显著,但指向性变化不明显。3)随着俯仰角的变化,声场的声压幅值出现明显的频移现象。
实验结果与上述旋转声源声场特性的数值计算和仿真得出的结果一致,验证了此方法的有效性和精确性。但实验数据与数值仿真的声压数值方面存在一定的误差,这是因为半消声室存在一定的背景噪声,对实验结果有一定的影响。风扇周围的支架会对辐射声场产生散射,影响总辐射场。
4 结论1) 给出了旋转声辐射声压解析表达式,探讨了点源、偶极子源、克希荷夫源的构建关系及其声压表达式的解析过程。
2) 给出了任意条件下解析旋转声场谐波阶次的精确截断和门限值,提高了预估精度和计算效率。
3) 数值仿真上述理论分析,得到旋转声场具有多普勒效应,并给出了旋转声场的声场特性和指向性特征,讨论了旋转马赫数、基频、声源半径等关键影响因素对旋转声场的影响及旋转源与克希荷夫源之间的等价性关系。
4) 在半消声室内对风扇叶片工作时产生的声场进行实验测试,测试结果与仿真一致,验证了本文提出方法的有效性。研究结果对低噪声旋转机械结构设计和辐射噪声测量具有重要的参考价值。
| [1] |
LIGHTHILL M J. On sound generated aerodynamically I. General theory[J]. Proceedings of the Royal Society of London Series A Mathematical Physical Sciences and Physical Sciences, 1952, 211(1107): 564. DOI:10.1098/rspa.1952.0060 |
| [2] |
LOWSON M V. The sound field for singularities in motion[J]. Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences, 1965, 286(1407): 559. DOI:10.1098/rspa.1965.0164 |
| [3] |
PRIEUR J, RAHIER G. Addendum to "Aeroacoustic integral methods, formulation and efficient numerical implementation"[Aerospace Science and Technology 5(2001)457-468][J]. Aerospace Science and Technology, 2002, 6(5): 323. DOI:10.1016/S1270-9638(02)01167-7 |
| [4] |
BRENTNER K S, FARASSAT F. Modeling aerodynamically generated sound of helicopter rotors[J]. Progress in Aerospace Sciences, 2003, 39(2/3): 83. DOI:10.1016/S0376-0421(02)00068-4 |
| [5] |
KESSLER M, WAGNER S. Source-time dominant aeroacoustics[J]. Computers & Fluids, 2004, 33(5/6): 791. DOI:10.1016/j.compfluid.2003.06.012 |
| [6] |
居鸿宾, 钟芳源. 旋转体源声辐射的近场分析[J]. 航空动力学报, 1995, 10(2): 131. JU Hongbin, ZHONG Fangyuan. Near sound field analysis of a rotating source[J]. Journal of Aerospace Power, 1995, 10(2): 131. DOI:10.13224/j.cnki.jasp.1995.02.007 |
| [7] |
吴九汇, 陈花玲, 黄协清. 旋转点声源空间声场的频域精确解[J]. 西安交通大学学报, 2000, 34(1): 71. WU Jiuhui, CHEN Hualing, HUANG Xieqing. Acoustic solution of rotating point source in frequency domain[J]. Journal of Xi'an Jiaotong University, 2000, 34(1): 71. DOI:10.3321/j.issn:0253-987X.2000.01.017 |
| [8] |
MAO Yijun, GU Yuanyuan, QI Datong, et al. An exact frequency-domain solution of the sound radiated from the rotating dipole point source[J]. The Journal of the Acoustical Society of America, 2012, 132(3): 1294. DOI:10.1121/1.4742972 |
| [9] |
刘志红. 声辐射预估理论及其应用研究[D]. 青岛: 青岛理工大学, 2010 LIU Zhihong. Investigation on the Theory and Its Application of Sound Radiation Prediction[D]. Qingdao: Qingdao University of Technology, 2010 |
| [10] |
刘志红, 仪垂杰, 周扬民, 等. 旋转声源声辐射预估方法研究[C]//2011国际功能制造与机械动力学会议暨中国振动工程学会机械动力学学会成立30周年庆祝会议. 杭州: 机械动力学理论及其应用, 2011: 232
|
| [11] |
刘志红, 仪垂杰. 旋转运动声辐射的解析方法[J]. 机械设计与制造, 2015(12): 65. LIU Zhihong, YI Chuijie. The analytic method for calculating sound radiation from rotating sources[J]. Machinery Design & Manufacture, 2015(12): 65. DOI:10.19356/j.cnki.1001-3997.2015.12.019 |
| [12] |
宋正旋, 方一红. 亚声速射流轴对称模态的声辐射研究[J]. 空气动力学学报, 2022, 40(6): 102. SONG Zhengxuan, FANG Yihong. Acoustic radiation of axisymmetric mode in subsonic jets[J]. Acta Aerodynamica Sinica, 2022, 40(6): 102. DOI:10.7638/kqdlxxb-2021.0260 |
| [13] |
POLETTI M A. Series expansions of rotating two and three dimensional sound fields[J]. The Journal of the Acoustical Society of America, 2010, 128(6): 3363. DOI:10.1121/1.3506352 |
| [14] |
POLETTI M A, TEAL P D. Comparison of methods for calculating the sound field due to a rotating monopole[J]. The Journal of the Acoustical Society of America, 2011, 129(6): 3513. DOI:10.1121/1.3589481 |
| [15] |
CARLEY M. Series expansion for the sound field of rotating sources[J]. The Journal of the Acoustical Society of America, 2006, 120(3): 1252. DOI:10.1121/1.2221410 |
| [16] |
许坤波. 航空叶轮机管道声模态识别的数值及实验研究[D]. 西安: 西北工业大学, 2018 XU Kunbo. Numerical and experimental study on turbo-machinery ducted mode identification[D]. Xi'an: Northwestern Polytechnical University, 2018. DOI: 10.27406/d.cnki.gxbgu.2018.000257 |
| [17] |
曾向阳, 薛旭瑞, 王海涛. 基于声源叠加原理的大型号角扬声器声辐射特性分析[J]. 西北工业大学学报, 2013, 31(6): 853. ZENG Xiangyang, XUE Xurui, WANG Haitao. Numerical analysis of sound emission characteristics of large horn-L oaded loudspeaker based on source superposition model[J]. Journal of Northwestern Polytechnical University, 2013, 31(6): 853. DOI:10.3969/j.issn.1000-2758.2013.06.005 |
| [18] |
POLETTI M A. Spherical coordinate descriptions of cylindrical and spherical Bessel beams[J]. The Journal of the Acoustical Society of America, 2017, 141(3): 2069. DOI:10.1121/1.4978787 |
| [19] |
CHEN Xu, MAO Yijun, QI Datong. Frequency-domain acoustic pressure formulation for rotating source in uniform subsonic inflow with arbitrary direction[J]. Journal of Sound and Vibration, 2014, 333(14): 3081. DOI:10.1016/j.jsv.2014.03.004 |
| [20] |
高建正. 旋转叶片气动偶极子声源的可视化定位方法研究[D]. 上海: 上海交通大学, 2020 GAO Jianzheng. Theoretical study on the visualization of dipole source on rotating blades[D]. Shanghai: Shanghai Jiao Tong University, 2020. DOI: 10.27307/d.cnki.gsjtu.2020.000045 |
| [21] |
FENG Jianxiong, LIU Yangfan, LI Kaiming. Efficient frequency domain method for holographic localization of rotating sound sources with arbitrary array configurations[J]. Journal of Sound and Vibration, 2023, 544: 117374. DOI:10.1016/j.jsv.2022.117374 |
| [22] |
付建, 李海峰, 于海洋, 等. 管道风扇气动噪声数值计算方法[J]. 舰船科学技术, 2023, 45(2): 71. FU Jian, LI Haifeng, YU Haiyang, et al. Numerical predicting method of ducted fan aeroacoustics noise[J]. Ship Science and Technology, 2023, 45(2): 71. DOI:10.3404/j.issn.1672-7649.2023.02.013 |
| [23] |
CARESTA M, KESSISSOGLOU N. Effect of eccentric axial excitation from the propulsion system on the sound radiation of a submarine hull[C]//Proceedings of the 37th International Congress and Exposition on Noise Control Engineering. Shanghai: Institute of Noise Control Engineering, 2008: 4701
|
| [24] |
ZHAO Dan, WU Qiong, GAN Minyao, et al. Vibration and sound radiation of cylindrical shell covered with a skin made of micro floating raft arrays excited by turbulence[J]. Computer Modeling in Engineering & Sciences, 2023, 134(3): 2041. DOI:10.32604/cmes.2022.021026 |
| [25] |
ZHANG Y N, ZHANG M M, CAI C, et al. Aerodynamic load control on a dynamically pitching wind turbine airfoil using leading-edge protuberance method[J]. Acta Mechanica Sinica, 2020, 36(2): 275. DOI:10.1007/s10409-020-00939-2 |
| [26] |
ZHENG Hao, ZHAO Guozhong, SHANG Linyuan, et al. Topology optimization of bi-material curved shell structures for minimizing time-domain sound radiation[J]. International Journal for Numerical Methods in Engineering, 2022, 123(11): 2530. DOI:10.1002/nme.6949 |
| [27] |
YANG W, CHOY Y, WANG Z, et al. Sound radiation and resonators[J]. Mechanical Systems and Signal Processing, 2022, 165: 108408. DOI:10.1016/j.ymssp.2021.108408 |
| [28] |
JEON W H, LEE D J. A numerical study on the flow and sound fields of centrifugal impeller located near a wedge[J]. Journal of Sound and Vibration, 2003, 266(4): 785. DOI:10.1016/S0022-460X(02)01357-3 |
 2024, Vol. 56
2024, Vol. 56


