Standard Adomian Decomposition Method (ADM) is a useful and easy method to solve linear and nonlinear, delay, integral, partial, deterministic or stochastic differential equations accurately [1-4]. ADM has been applied in various engineering fields such as the fragmentation and aggregation and population balance equations [5], the KdV-like wave equation [6] and the Lane-Emden equations [7-8], etc. It is shown that ADM has an important advantage in that it can provide series solutions. Its modifications [9-13] have been also used to solve some linear and nonlinear ordinary differential equations. However, considering computer overflow problems, the finite terms series solution can be obtained from ADM. Thus the convergence of the solution would be improved by increasing the suitable number of truncated terms. M.M.Hosseini et al. [14] introduced an efficient ADM modification of ADM for providing the solution in a rapid convergent series. For strongly nonlinear and chaotic systems, ADM has been used in combination with numerical techniques for solving analytic solution[15-18]. The integration is different from the discretized approximation of true solution of purely numerical technique like the Runge-Kutta method [15]. Meanwhile, small interval length affects computation time, while big interval length would reduce convergence. The purpose of this paper is to develop a recursive algorithm based on ADM with suitable truncation order to make efficient use of the maximum stable step-size for good convergence.
In this paper, the recursive algorithm makes up of two consecutive stages. The analytic stage is based on standard Adomian Decomposition Method. Furthermore, it not only obtains a continuous functional form of the series solution but also transforms the analytic series expression into the matrix by using Differential Transformation (DT) theory. The numeric stage is the maximum stable step-size algorithm using the recursion percent error (RPE). By iterative computing, the analytic approximated solution turns the precise numerical solution over long time intervals. By the proposed algorithm, two nonlinear differential examples are provided. They are the second-order equation and the coupling equations. The simulation comparisons between the modified method solution and MATLAB@ ODE45 solution are shown that the recursive algorithm has the versatility and widely applicability.
2 Standard Adomian Decomposition MethodStandard ADM splits the differential equation into linear, remainder and nonlinear parts, as follows:
| ${\text{Nu + Lu + Ru = g(t)}}$ | (1) |
where N is a nonlinear operator; L is the highest-order derivative which is invertible; R is a linear differential operator of less order than L and g is the source term[18-19].
The ADM also consists of multiplying the integral operator L-1 on both sides of Eq.(1), decomposing the nonlinear part in terms of Adomian polynomials, and solving the successive terms of the series solution. So we write
| ${\text{u = }}\sum\limits_{n = 0}^\infty {{u_n}} , Nu = \sum\limits_{n = 0}^\infty {{A_n}} $ | (2) |
The definition of Adomian polynomials L is provided by the formula:
| ${A_n} = \frac{1}{{n!}}{\left[ {\frac{{{d^n}}}{{d{\lambda ^n}}}N\left( {\sum\limits_{n = 0}^\infty {{\lambda ^n}{u_n}} } \right)} \right]_{\lambda = 0}}$ | (3) |
Considering the initial value problems, the integral operator L-1 can be regarded as definite integrals form t0 to t [1]. If the dynamical system model is a second-order nonlinear differential equation, there exist two initial values U and
| $\phi (t) = U + {U^t}$ | (4) |
where Φ(t) satisfies LΦ=0.
Consequently, U is identified in the recursion way
| $\left\{ \begin{align} & {{u}_{0}}={{L}^{-1}}\left( g \right)+\Phi \left( t \right) \\ & {{u}_{k+1}}=-{{L}^{-1}}\left( R{{u}_{k}} \right)-{{L}^{-1}}\left( N{{u}_{k}} \right), k0 \\ \end{align} \right.$ | (5) |
If the series solution converges in a suitable way, U is defined as $u = \mathop {\lim }\limits_{\gamma \to + \infty } {\Psi _\gamma }\left( t \right)$, where ${\Psi _\gamma } = \sum\limits_{i = 0}^\gamma {{u_i}} $[19].Considering computer overflow problems, we can only obtain the (γ+1) terms approximated solution Ψγ in practice. γ is defined as truncation order.
3 Recursive Algorithm Based on ADMThe main advantage of the standard ADM is that it is versatile and can be used directly to solve strongly nonlinear and chaotic systems. Generally, the choice of the highest-order derivative for L guarantees the algorithm is easy to realize. But compared with inverting the entire linear operator, convergence is much lower[15]. Numerical iteration should be integrated to provide global convergence. Furthermore, analytic-numeric ADM also needs to keep higher accuracy by choosing small step-size or by adding series more terms. If the truncation order γ small, an analytic approximated solution can be easily derived using ADM. But small truncation order only allows small step-size. As truncation order increases, the task of calculation in computer simulations may become difficulty and encounter overflow problems.
In order to integrate ADM and numerical algorithm, the time variable t is divided into segments 0=t0&t1&…&tk&…&t=T and h k=tk-tk-1(k=1, …, ø), h k is defined as step-size. Then the analytic solution containing initial values, step-size h k and cumulative time tk-1 is deduced in the form of series based on ADM. For the second-order nonlinear differential equation, Uk-1 and
| $\left\{ \begin{align} & {{U}_{k}}={{\left[ \sum\limits_{n=0}^{\gamma }{{{u}_{n}}\left( t \right)} \right]}_{t={{\hbar }_{k}}}}={{\Phi }_{k-1}}\left( {{\hbar }_{k}} \right)+ \\ & {{L}^{-1}}{{\left[ \sum\limits_{n=0}^{\gamma }{{{g}_{n}}\left( {{t}_{k-1}} \right){{t}^{n}}-R\sum\limits_{n=0}^{\gamma -1}{{{u}_{n}}\left( t \right)-\sum\limits_{n=0}^{\lambda -1}{{{A}_{n}}\left( t \right)}}} \right]}_{t={{\hbar }_{k}}}} \\ & {{{\hat{U}}}_{k}}={{{{\Phi }'}}_{k-1}}\left( {{\hbar }_{k}} \right)+ \\ & {{L}^{-1}}{{\left[ \sum\limits_{n=0}^{\gamma }{{{{{g}'}}_{n}}}\left( {{t}_{k-1}} \right){{t}^{n}}-R\sum\limits_{n=0}^{\gamma -1}{{{{{u}'}}_{n}}\left( t \right)}\text{-}\sum\limits_{n=0}^{\gamma -1}{{{{{A}'}}_{n}}\left( t \right)} \right]}_{t={{\hbar }_{k}}}} \\ \end{align} \right.$ | (6) |
where Φk-1(hk)=Uk-1+
For the double coupling equations, Eq.(6) can be rewritten as
| $\begin{align} & {{U}_{x, k}}={{\Phi }_{x, k-1}}\left( {{\hbar }_{k}} \right)+ \\ & {{L}^{-1}}{{\left[ \sum\limits_{n=0}^{\gamma }{{{g}_{x, n}}\left( {{t}_{k-1}} \right){{t}^{n}}-{{R}_{x}}\sum\limits_{n=0}^{\gamma }{{{u}_{x, n}}\left( t \right)-\sum\limits_{n=0}^{\gamma }{{{A}_{x, n}}\left( t \right)-\sum\limits_{n=0}^{\gamma -1}{{{B}_{y, n}}\left( t \right)}}}} \right]}_{t={{\hbar }_{k}}}} \\ \end{align}$ | (7) |
where x and y indicate different coupling variables of the dynamical systems. $\sum\limits_{n = 0}^\gamma {{B_{y, n}}} \left( t \right)$ are coupling terms between ux, n and uy, n.
Note that the cumulative timetk-1 should be taken to Taylor series expansion of g(t), that is g(t)=$\sum\limits_{n = 0}^\gamma {{g_n}} \left( {{t_{k - 1}}} \right){t^n}$.
Step-size hk and truncation order γ have effect on convergence and accuracy of this method. Therefore, it is necessary to analyze the influence of different parameters on convergence of the algorithm.
Within individual interval, Ψγ is a function of time t. Based on Differential Transformation theory, solution component un of Ψγ is differentiated continuously with respect to time t [20-21]. Thus it follows that
| ${\zeta _{n.m}} = \frac{1}{{m!}}{\left[ {\frac{{{d^m}}}{{d{t^m}}}{u_n}\left( t \right)} \right]_{t = 0}}$ | (8) |
Based on Eq.(8), un is converted to un=$\sum\limits_{k = 0}^m {{\xi _{n, {k^{{t^k}}}}}} $. Furthermore, Eq.(5) can be formulated as
| ${\text{U = }}\Theta \bullet \Gamma $ | (9) |
Where U=[u0, u1, …, uγ]T∈Rγ+1, Γ=[t0, t, …, tm]T∈Rm+1, Θ=[θ0, θ1, …, θγ]T∈R(γ+1)×(m+1), θi=[ξi, 0, ξi, 1, …, ξi, m]∈Rm+1, i=0, 1, …, m. Where Θ is called the coefficient matrix of Adomian analytic solution. The new constructed solution representation of Ψγ can speed up the computation and lay the foundation for implementations of the recursive algorithm.
Numeric-analytic algorithm has the conflict between truncation order γ and step-size h k. Therefore, in order to improve convergence and speed up computation, a modified maximum stable step-size algorithm is presented considering recursion-stopping criterion.
Let ζtol be the user-defined minimal tolerated recursion percent error, h init be the user-defined initial value of step-size, γmax be the user-defined maximal value of γ.
Then the truncation error of analytic solution is given so that:
| $error = \left| {u - \sum\limits_{n = o}^\gamma {{u_n}} } \right| = \left| {\sum\limits_{n = \gamma + 1}^\infty {{u_n}} } \right|$ | (10) |
Without loss of generality, the recursion percent error of the γ-th term is defined as
| ${\xi _{ra}} = \left| {{u_\gamma }\left( h \right)} \right|/\left| {\sum\limits_{i = 0}^\gamma {{u_n}} } \right| = \left| {\sum\limits_{n = \gamma + 1}^\infty {{\xi _{\gamma , {k^{{h^k}}}}}} } \right|/\left| {\sum\limits_{i = 0}^\gamma {\sum\limits_{k = 0}^m {{\xi _{i, {k^{{h^k}}}}}} } } \right|$ | (11) |
And h init is substituted into Eq.(11). ζra is used to be compared with ζtol. Then the small truncation order in each interval and the large step-size over long time intervals can be realized as follows:
(1) When γ≤γmax and ζra≤ζtol, γ and h init is accepted successfully. If the system model is coupling equations, ζra needs to be discussed. At least two ζra can be obtained from different variables of the coupling equations. For different coupling variables, coupling terms determine the different ADM analytic solutions so that different Θ can be constructed. But the same step-size requires the only ζ~, where ζ~=ζtol/ζra. The new h init in next interval is computed [18]
| ${h_{k + 1}} = 0.9 \cdot {h_k}{\left( \xi \right)^{1/\left( {\gamma + 1} \right)}}, k = 1, \ldots , \phi $ | (12) |
(2) When ζra>ζtol and γ>γmax, the step-size h init shall be multiplied by η(η<1), and then compute the solution again and check ζra. If the step-size h init is too small, we need to reconstruct the matrix Θ and repeat in each interval.
Remark 1 If ζra=0, we ignore the γ-th term and compute next term. Furthermore, for multivariate coupling equations, when there are more recursion percent errors, the errors would be used to compute the average value or optimal value for the only ζ~.
The maximum stable step-size algorithm is mechanized by MATLAB@ symbolic toolbox. The concrete steps are concluded as follows:
1) Use “syms” function to define the structure $\sum\nolimits_{n = 0}^\infty {{u_n}} and\sum\nolimits_{n = 0}^\infty {{A_n}} $.
2) Solve the first (γ+1) term analytic series solution and convert the coefficient of approximated solution into Θ, recursively.
3) Determine the reasonable the value of ζtol, h init and γmax. Substitute initial values and system parameters values into Θ in individual interval, using “subs” function.
4) Apply numeric-analytic ADM scheme to compute numeral results of nonlinear equations iteratively.
Remark 2 The above steps are convenient for solving nonlinear differential equations. Using MATLAB@ symbolic toolbox, recursive matrix Θ can be determined easily. To realize the useful recursive algorithm, it is found that the new weight information that comes from γ-th term is apparently formulated by ζtol, which can be used to monitor the truncation error. This new information is utilized to obtain stable maximum step-size and recursion term. It is not necessary for initial value problems to compute Adomian solution in each interval repeatedly and the convergence of different intervals can be improved.
4 Simulation ExamplesExample 1 Considering the well-known damped Duffing oscillator:
| $\frac{{{d^2}u}}{{d{t^2}}} + \frac{{du}}{{dt}} + u + {u^3} = 0, u\left( 0 \right) = 1, \mathop u\limits^ \left( 0 \right) = 0$ | (13) |
Assuming initial values be unknown parameters, we obtain each solution component of U by computation
| $\begin{align} & {{u}_{0}}=u\left( 0 \right)+\dot{u}\left( 0 \right)t \\ & {{u}_{1}}=-0.5{{t}^{2}}\left( {{u}^{3}}\left( 0 \right)+{{u}^{2}}\left( 0 \right)\dot{u}\left( 0 \right)t+ \right. \\ & 0.5u\left( 0 \right){{{\dot{u}}}^{2}}\left( 0 \right){{t}^{2}}+u\left( 0 \right)+0.1\text{ }{{{\dot{u}}}^{3}}\left( 0 \right){{t}^{3}}+ \\ & \left. 0.33\dot{u}\left( 0 \right)t+\dot{u}\left( 0 \right) \right) \\ & {{u}_{2}}=0.167{{t}^{3}}\left( {{u}^{3}}\left( 0 \right)+u\left( 0 \right)+\dot{u}\left( 0 \right) \right)+\ldots + \\ & 0.002l{{u}^{5}}\left( 0 \right){{t}^{9}} \\ & {{u}_{3}}=-0.042{{t}^{4}}\left( \overset{\left( 0 \right)}{\mathop{\text{ }u}}\, +{{u}^{3}}\left( 0 \right)+u\left( 0 \right) \right)-\ldots - \\ & 0.000088{{{\dot{u}}}^{7}}\left( 0 \right){{t}^{13}} \\ & \cdots \\ \end{align}$ | (14) |
As truncation order increases, the derivation of component solution becomes extremely complicated. By ADM, the second-order or higher-order systems have to be paid attention to computation speed.
Then the coefficient matrix Θ is constructed as
| $\Theta = \left[ {\begin{array}{*{20}{c}} {u\left( 0 \right)}&{\mathop u\limits^ \left( 0 \right)}& \ldots &0\\ 0&0& \ldots &0\\ \vdots & \vdots & \vdots & \vdots \\ 0&0& \ldots &{0.0051{u^2}\left( 0 \right)\mathop {{u^7}\left( 0 \right) + {{4.68710}^{ - 5}}{u^7}\left( 0 \right)}\limits^. } \end{array}} \right]$ | (15) |
Considering the computation complexity, the algorithm parameters is set hinit=0.8, γmax=4.
MATLAB@ ODE45 is the adaptive variable step-size Runge-Kutta function from MATLAB. We regard small-step ODE45 solution as true solution and compare the proposed algorithm with the ODE45.
Local convergence of ADM is shown in Fig. 1. The convergence radius of ADM 4-term solution is estimated to 0.6. And the departure time of ADM 24-term solution is 1.2 s. The ADM 24-term solution has better convergence than 4-term. The truncation order has great influence on convergence capability. However, the simulation elapsed time of computing the 4-term and 24-term are about 23.8 s and 295.8 s, respectively. It is indicated that the suitable truncation order can speed up computation and improve convergence.

|
Figure 1 Comparison of solutions by ODE45 and standard ADM |
Different step-sizes curves of the 4-term ADM approximation are shown in Fig. 2. The curve for hk=0.8 starts to deviates from the ODE45 curve. The curve for h k=1 is inadequate to remain the same. Simulation results indicate that the larger step-size can lead the lower computation accuracy of the method. Fixed step-size is inadequate to be applied in different subintervals. Hence, without loss of generality, variable step-size is of importance considerable.

|
Figure 2 Influence of different step-sizes on the computation result of the 4-term approximation |
Fig. 3 shows a comparison of standard ADM and ODE45 with h k=0.4. Although the larger truncation order would get higher computation accuracy, there is no need to choose much more larger truncation order γ. Herein, the truncation order is set to 3 or 4.
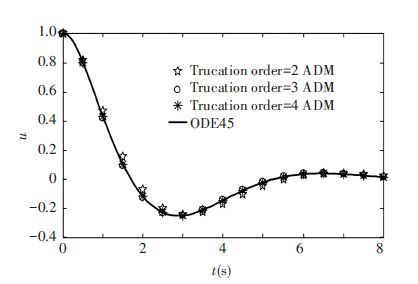
|
Figure 3 Influence of different truncation term number on the computation result of standard ADM |
Fig. 4 is plotted to compare the proposed algorithm with the ODE45 and fixed step-size ADM on [0, 25]. The fixed step-size is set to 0.5s. In the figure, the influence of ζtol on the step-size is analyzed. When ζtol changes from 0.01 to 0.1, the step-size gradually exceeds 0.5 s. Meanwhile, the results contrasts imply that the modified algorithm effectively coincides with ODE45. The maximum error of the fixed step-size ADM is 0.01 9. Combined with Table 1, the errors comparison is listed to validate the accuracy of modified solution. Absolutely the errors would be more accurate if a smaller recursion percent error ζtol is used.
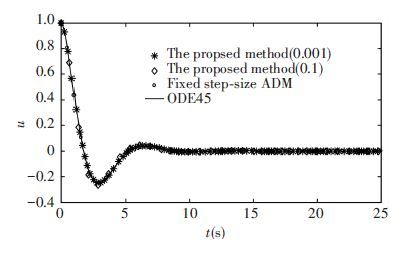
|
Figure 4 The comparison of the ODE45 solution, fixed step-size ADM and the proposed algorithm |
| Table 1 The comparison of the proposed algorithm’s solution with ODE45 solution and its error |
Example 2 Consider the forced coupling equations
| $\left\{ \begin{array}{l} {\mathop u\limits^{..} _x} + b{\mathop u\limits^. _x} + \beta {u_x} + u_x^3 = \sigma \cos \omega t + {q_1}{u_y}\\ {\mathop u\limits^{..} _y} + b{\mathop u\limits^. _y} + \beta {u_y} + u_y^3 = \sigma \cos \omega t + {q_1}{u_x} \end{array} \right.$ | (16) |
where b, β, q1 and q2 are system structure parameters. σ and ω are amplitude and angular frequency of periodic excitation. The parameter variations affect nonlinear character of dynamical system.
We take initial time tk-1 of each interval to Taylor series expansion of the excitation function g(t), that is g(t)=$\sum\limits_{n = 0}^\gamma {{g_n}\left( {{t_{k - 1}}} \right){t^n}} $. The system parameters are chosen as
| $b = 0.2, \beta = 1, {q_1} = 0.4, {q_2} = 0.6$ |
Hence initial values and σ are considered to be unknown. As the system of Eq.(16) is symmetrical structure, ux and uy have the similar analytical expression. Each solution components of ux and u·x are derived
| $\begin{align} & {{u}_{x, 0}}=0.5\sigma {{t}^{2}}\cos \left( {{t}_{k-1}} \right)+\overset{.}{\mathop{\text{ }u}}\, \left( 0 \right)t+{{u}_{x}}\left( 0 \right) \\ & {{u}_{x, 1}}=0.1{{t}^{2}}\left( 2{{u}_{y}}\left( 0 \right)-5u_{x}^{3}\left( 0 \right)-5{{u}_{x}}\left( 0 \right)-\overset{.}{\mathop{{{u}_{x}}}}\, \left( 0 \right) \right)+\ldots - \\ & 0.0022{{t}^{8}}{{\sigma }^{3}}{{\cos }^{3}}\left( {{t}_{k}}-1 \right) \\ & {{u}_{x, 2}}=0.0067{{t}^{3}}\left( \overset{.}{\mathop{{{u}_{x}}}}\, \left( 0 \right)-2{{u}_{y}}\left( 0 \right)+5u_{x}^{3}\left( 0 \right)+5{{u}_{x}}\left( 0 \right) \right)+ \\ & \ldots +9.198\times {{10}^{-4}}{{t}^{13}}{{\sigma }^{5}}{{\cos }^{5}}\left( {{t}_{k}}-1 \right) \\ & \vdots \\ \end{align}$ | (17) |
And
| $\begin{align} & {{{\dot{u}}}_{x, 0}}=\sigma {{t}^{2}}\cos \left( {{t}_{k-1}} \right)+\overset{.}{\mathop{\text{ }u}}\, \left( 0 \right) \\ & {{{\dot{u}}}_{x}}\left( 0 \right){{u}_{x, 1}}=0.2{{t}^{2}}\left( 2{{u}_{y}}\left( 0 \right)-5u_{x}^{3}\left( 0 \right)-5{{u}_{x}}\left( 0 \right)-\overset{.}{\mathop{{{u}_{x}}}}\, \left( 0 \right) \right)+\ldots \\ & -0.0176{{t}^{7}}{{\sigma }^{3}}{{\cos }^{3}}\left( {{t}_{k}}-1 \right) \\ & {{{\dot{u}}}_{x, 2}}=0.020{{t}^{2}}\left( \overset{.}{\mathop{{{u}_{x}}}}\, \left( 0 \right)-2{{u}_{y}}\left( 0 \right)+5u_{x}^{3}\left( 0 \right)+5{{u}_{x}}\left( 0 \right) \right)+\ldots + \\ & 1.288\times {{10}^{-4}}{{t}^{13}}{{\sigma }^{5}}{{\cos }^{5}}\left( {{t}_{k}}-1 \right) \\ & \vdots \\ \end{align}$ | (18) |
For this kind of coupling system, specific parameters of modified variable step-size algorithm are obtained
| ${h_{init}} = 0.3, {\gamma _{\max }} = 4, {\zeta _{tol}} = 0.01$ |
Two independent variables in coupling system are considered in this example. Here ζx, ra and ζy, ra represent the recursion percent error of ux and uy, respectively. In the iterative calculation of the continuous numerical solution, ζra is fully taken account. We take ζra=(ζx, ra+ζy, ra)/2.
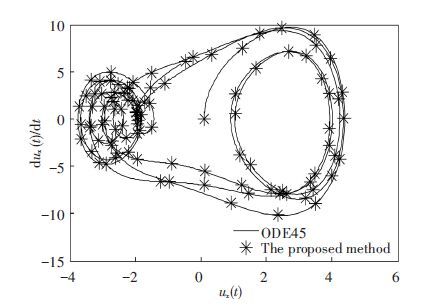
The variation of step-size and truncation order is shown in Fig. 5. As iterations number increases, step-size changes from 0.1 s to 0.3 s. Basically truncation order is 4. These results corroborates that the modified algorithm is different from the fixed step-size method and the fixed truncation order method. We purposefully select σ=27 and initial values (0.1, 0, 0.1, 0). Then variable order and step-size numerical solutions are obtained easily. From Figs. 6 and 7, the curves of ux and u·x match well with the curves of ODE45. The trajectory variations around the focus can be seen from phase portraits between ux and u·x in Fig. 8. It is demonstrated that the coupling system has the chaos phenomenon when σ is equal to 27. The comparison simulation indicates that the recursive algorithm is more feasible and widely used to analyze the dynamical nonlinear system.
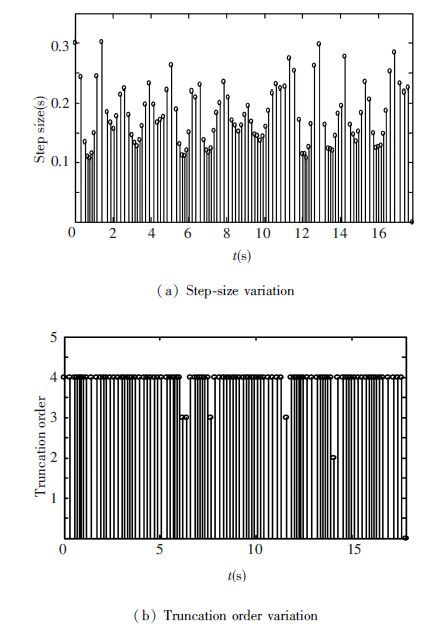
|
Figure 5 Variation of the proposed algorithm over long time intervals |
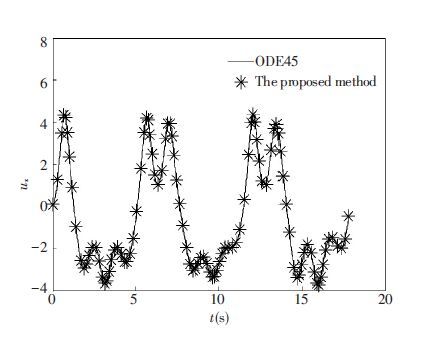
|
Figure 6 Solutions comparison of ux by the proposedalgorithm and ODE45 for σ=27 |

|
Figure 7 Solutions comparison of u·x by the proposed algorithm and ODE45 for σ=27 |
|
Figure 8 Phase portraits by the proposed algorithm with ODE45 for σ=27 |
5 Conclusions
In the paper, the recursive algorithm has the advantage of offering a continuous functional form of Adomian series solution. Moreover, Differential Transformation (DT) theory is made use of to convert analytic solution from the complex series expression to matrix form. Then instead of using the fixed truncation order or fixed step-size, the recursion percent error has been defined to develop a maximum stable step-size criterion for good convergence. The second-order damped Duffing equation and coupling Duffing equations are solved as examples. Comparison results with ODE45 solution indicate that the recursive algorithm has good dependability and popularization for dynamical system analysis.
| [1] |
Adomian G. A review of the decomposition method and some recent results for nonlinear equations.
Mathematical and Computer Modelling,1990, 13 (7) : 17-43.
( 0) 0)
|
| [2] |
Singh R, Kumar J. The Adomian decomposition method with Green’s function for solving nonlinear singular boundary value problems.
Journal of Applied Mathematics and Computing,2014, 44 (1/2) : 397-416.
( 0) 0)
|
| [3] |
Duan J S, Rach R. A new modification of the Adomian decomposition method for solving boundary value problems for higher order nonlinear differential equations.
Applied Mathematics and Computation,2011, 218 (8) : 4090-4118.
( 0) 0)
|
| [4] |
Gu Huifeng, Li Zhibin. A modified Adomian method for system of nonlinear differential equations.
Applied Mathematics and Computation,2007, 187 (2) : 748-755.
( 0) 0)
|
| [5] |
Singh R, Saha J, Kumar J. Adomian decomposition method for solving fragmentation and aggregation population balance equations.
Journal of Applied Mathematics and Computing,2015, 48 (1) : 265-292.
( 0) 0)
|
| [6] |
Sohail A, Maqbool K, Hayat T. Painlevé property and approximate solutions using Adomian decomposition for a nonlinear KdV-like wave equation.
Applied Mathematics and Computation,2014, 229 : 359-366.
( 0) 0)
|
| [7] |
Wazwaz A M, Rach R, Duan J S. Adomian decomposition method for solving the Volterra integral form of the Lane-Emden equations with initial values and boundary conditions.
Applied Mathematics and Computation,2013, 219 (10) : 5004-5019.
( 0) 0)
|
| [8] |
Rach R, Wazwaz A M, Duan J S. The Volterra integral form of the Lane-Emden equation: new derivations and solution by the Adomian decomposition method.
Journal of Applied Mathematics and Computing,2014 : 1-15.
( 0) 0)
|
| [9] |
Jafari H, Daftardar-Gejji V. Revised Adomian decomposition method for solving a system of nonlinear equations.
Applied Mathematics and Computation,2006, 175 (1) : 1-7.
( 0) 0)
|
| [10] |
Wazwaz A M, El-Sayed S M. A new modification of the Adomian decomposition method for linear and nonlinear operators.
Applied Mathematics and Computation,201, 122 (3) : 393-405.
( 0) 0)
|
| [11] |
Lin Yezhi, Liu Yinping, Li Zhibin. Symbolic computation of analytic approximate solutions for nonlinear differential equations with initial conditions.
Computer Physics Communications,2012, 183 (1) : 106-117.
( 0) 0)
|
| [12] |
Pue-on P, Viriyapong N. Modified Adomian decomposition method for solving particular third-order ordinary differential equations.
Applied Mathematical Sciences,2012, 6 (30) : 1463-1469.
( 0) 0)
|
| [13] |
Hasan Y Q. ModifiedAdomian decomposition method for second order singular initial value problems.
Advances in Computational Mathematics and its Applications,2012, 1 (2) : 94-99.
( 0) 0)
|
| [14] |
Hosseini M M, Jafari M. A note on the use of Adomian decomposition method for high-order and system of nonlinear differential equations.
Commun Nonlinear Sci Numer Simulat,2009, 14 : 1952-1957.
( 0) 0)
|
| [15] |
Ghosh S, Roy A, Roy D. An adaptation of Adomian decomposition for numeric-analytic integration of strongly nonlinear and chaotic oscillators.
Computer Methods in Applied Mechanics and Engineering,2007, 196 (4) : 1133-1153.
( 0) 0)
|
| [16] |
Duan J S, Rach R. New higher-order numerical one-step methods based on the Adomian and the modified decomposition methods.
Applied Mathematics and Computation,2011, 218 (6) : 2810-2828.
( 0) 0)
|
| [17] |
Duan J S, Rach R. Higher-order numeric Wazwaz-El-Sayed modified Adomian decomposition algorithms.
Computers & Mathematics with Applications,2012, 63 (11) : 1557-1568.
( 0) 0)
|
| [18] |
Ramana P V, Prasad B K R. Modified Adomian Decomposition Method for Van der Pol equations.
International Journal of Non-Linear Mechanics,2014, 65 : 121-132.
( 0) 0)
|
| [19] |
Hosseini M M. Adomian decomposition method for solution of nonlinear differential algebraic equations.
Applied mathematics and computation,2006, 181 (2) : 1737-1744.
( 0) 0)
|
| [20] |
Gkdogan A, Merdan M, Yildirim A. Adaptive multi-step differential transformation method to solving nonlinear differential equations.
Mathematical and Computer Modelling,2012, 55 (3) : 761-769.
( 0) 0)
|
| [21] |
Chen C L, Liu Y C. Solution of two-point boundary-value problems using the differential transformation method.
Journal of Optimization Theory and Applications,1998, 99 (1) : 23-35.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


