2. School of Civil Engineering, Jilin Jianzhu University, Changchun 130118, China
Structural reliability methods deal with the statistical nature of many basic variables in structural safety analysis and design. Nowadays, they have been applied to structural design and reassessment of the safety of existing structures [1-3]. The Monte-Carlo simulation (MCS), the response surface approach and the sensitivity-based analysis are three methods that have been widely used to estimate the reliability of structures with implicit performance functions. The inherent disadvantage of MCS is unendurable computational cost and requiring a considerable amount of samples, and it will become excessively time consuming for very low probabilities of failure. The response surface method[4] is considered to be one of the most widely used methods in the structural reliability analysis. The RSM only uses a few selected simulations in the neighborhood of the most likely failure point, and obtains a polynomial approximation of the performance function, which is used to calculate the failure probability of the structure. But, when the traditional RSM method is adopted to deal with complex structural reliability problems, difficulties are encountered, such as parameter selection[5], accuracy and computation time[6]. Even the sensitivity-based reliability analysis approach is more elegant and more efficient than the simulation or RSM, it needs considerable programming and computational efforts.
In recent years, artificial neural network (ANN) algorithms[7] have been rapidly developed for performing function approximation. Scarselli and Tsoi[8]gave a survey of some universal approximation methods using feed-forward neural networks. More recently, the ANN technique was combined with the response surface methodology and other methods for structural reliability analysis [9-10]. Deng et al. [11]performed the reliability analysis of a mine pillar and geotechnical engineering structures by combining FEMs, ANN and MCS. Cheng et al. [12] developed an ANN-based RSM for predicting the failure probability of structures. Chatterjee and Bandopadhyay[13] performed the reliability analysis of a load-haul-dump (LHD) machine by combining genetic algorithm with ANN. The ANN has been widely used in structural reliability analysis, but the conventional feed-forward neural networks have the drawbacks such as difficulties in determining initial weights and the number of layers and processing elements. The convergence time is also long when they are trained with the back-propagation training algorithm. However, many researchers have been trying to solve the existing problems of conventional neural networks. Qian et al.[14] introduced the orthogonal network that applied distribution functions to transfer variables and improve the problems of local minimum and slow convergence speed. Zou et al.[15]applied the approximation theory of orthogonal functions to building networks. The training algorithm derived from Least-Squared Algorithm showed faster convergence speed than traditional back-propagation methods.
In this paper, a LONN-based RSM is proposed to calculate structural reliability with implicit performance. The LONN is used to approximate the relationship between the performance function and random variables. The values of the first-order partial derivatives of the performance function can be computed through the successful trained LONN, hence FORM can be used to calculate the failure probability of the structure. Since LONN has only one hidden layer and unique weights, the training rule can rapidly find the optimum weights, which are identical to the coefficients of the Legendre polynomials.
2 The LONN-Based Response Surface Method 2.1 Orthogonal FunctionsAccording to the theory of orthogonal functions[16-17], an arbitrary function fx can be expressed by a set of orthogonal polynomials, Φ=[φ1(x), φ2(x), …, φn(x)]T, hence,
| ${{F}_{n}}\left( x \right)=\sum\limits_{i=1}^{n}{{{\omega }_{i}}{{\varphi }_{i}}}\left( x \right)+R=W\Phi +R$ | (1) |
and
| $\underset{x\to \infty }{\mathop{\lim }}\, {{\int_{-1}^{1}{\left( f\left( x \right)-{{F}_{n}}\left( x \right) \right)}}^{2}}dx=0$ | (2) |
where
| $\begin{matrix} {{\omega }_{i}}\int_{-1}^{1}{f\left( x \right){{\varphi }_{i}}\left( x \right)dx/{{A}_{i}}} & i=1, 2, \cdots \\ \end{matrix}$ | (3) |
| $\int_{-1}^{1}{{{\varphi }_{i}}\left( x \right){{\varphi }_{j}}\left( x \right)dx=\left\{ \begin{matrix} \begin{matrix} 0 & i\ne j \\ \end{matrix} \\ \begin{matrix} {{A}_{i}} & i=j \\ \end{matrix} \\ \end{matrix} \right.}$ | (4) |
and R is the approximation error.
There are several orthogonal functions such as Fourier series, Hermit and Legendre polynomials. Each of them has its application domain in function approximation. In this paper, the Legendre polynomial function is adopted. The Legendre polynomial function set {L1(x), L2(x), L3(x), … }is orthogonal and has the recursive property as defined below
| $\begin{align} & i{{L}_{i+1}}\left( x \right)-\left( 2i-1 \right){{L}_{i}}\left( x \right)+ \\ & \begin{matrix} \left( i-1 \right){{L}_{i-1}}\left( x \right)\text{=}0 & i\ge 2 \\ \end{matrix} \\ \end{align}$ | (5) |
or
| ${{L}_{i+1}}\left( x \right)={{a}_{i}}x{{L}_{i}}\left( x \right)-{{b}_{i}}{{L}_{i-1}}\left( x \right)$ | (6) |
where L1(x)=1 and L2(x)=x, ai=2-$\frac{1}{i}$, bi=1-$\frac{1}{i}$, both ai and bi are constants.
The equations above indicate that an arbitrary function can be approximated by a set of Legendre polynomials, and the coefficient ωi is unique, which can be integrated if the function f(x) is known. However, the coefficient ωi may be also trained and obtained by using input and output data, that is x and F(x), if the Legendre polynomials are used to establish an orthogonal neural network.
2.2 Legendre Neural Network ModelLegendre neural network is an orthogonal neural network[18] based on the properties of orthogonal polynomials, which is a feed-forward network consisting of three layers, that is, input layer, single hidden layer and output layer, as shown in Fig. 1.

|
Figure 1 Legendre neural network model |
The network input signal is {x1, x2, …, xm} and the output is y=$\sum\limits_{i=1}^{n}{{}}$Φi(X)ωi, where Φi(X) are processing elements corresponding to Legendre polynomials and their respective weights are ωi, which can be trained to obtain the desired weights of Eq. (3). There are no weights between the middle layer and input layer. The i-th processing element of this linear neural network is corresponding to the i-th expansion item of the Legendre polynomials. Since the coefficients of all expansion terms are unique, hence the weights of this linear neural network will be unique. Therefore, the traditional ANN problems of local minimum and determination of the initial weights will be solved. Moreover, the orthogonal neural network is single-layer and linear.
The training algorithm used to search for optimum weights is derived from the gradient descent method, which is a popular method for generating learning algorithm[19].This algorithm can be applied to any continuous functions such as sigmoid, hyperbolic, tangent, and orthogonal functions, and has been proved that the training algorithm will always converge and find optimum weights.The optimum solution of the weights is identical to the unique coefficients of the expansion terms.More importantly, the training of the neural network will converge rapidly because the weights are unique.
2.3 The LONN-Based RSM with FORMIn the proposed method, the LONN is applied to approximate the performance function and its first-order partial derivatives. The role of LONN is similar to the polynomial function used in conventional RSM. The difference between the proposed method and the conventional RSM is that a set of polynomial functions are used in conventional RSM [20], while a series of activation functions, which have various expressions, are used in LONN model.
The explicit formulation of the approximate limit state function is derived by using the parameters (inputs, weights, scaled vales) of the proposed LONN model, and then, all necessary parameters can be obtained from the successfully trained LONN model. Once the explicit formation of the approximate performance function is established, the developed LONN model can be easily combined with a reliability method to predict the failure probability of structures. In the present study, the FORM is successfully linked to the developed LONN model. The computing procedure of the proposed method can be described as follows:
Step 1 Define the performance function, determine the random variables and specify their probabilistic characters, assume the initial values of the design point X*=(x1*, x2*, …, xn*), compute the corresponding values of the performance function g(x1(1), x2(1), …, xn(1)) and g(x1(1), …, xi(1)±fσi, …, xn(1)), where f=3 at the first iteration and f=1 hereafter.
Step 2 Use the uniform design method to obtain the suitable training datasets. Compute the mean value μXiN and standard deviation σXiN at the design point of the equivalent normal distribution for those variables that are non-normal distributed. The transformation formulae will be
| $\mu _{{{X}_{i}}}^{N}=x_{i}^{*}-{{\Phi }^{-1}}\left[ {{F}_{{{X}_{i}}}}\left( x_{i}^{*} \right) \right]\sigma _{{{X}_{i}}}^{*}$ | (7) |
| $\sigma _{{{X}_{i}}}^{N}=\varphi \left\{ {{\Phi }^{-1}}\left[ {{F}_{{{X}_{i}}}}\left( x_{i}^{*} \right) \right] \right\}/{{f}_{{{X}_{i}}}}\left( x_{i}^{*} \right)$ | (8) |
where FXi(xi*) and fXi(xi*) are distribution function and probability density function respectively; Φ(·) and Φ-1(·) are standard normal distribution function and its inverse function respectively; φ(·) is the normal probability density function. The coordinates of the design point in the equivalent standard normal space are
| $x_{i}^{'*}=\frac{x_{i}^{*}-\mu _{{{X}_{i}}}^{N}}{\sigma _{{{X}_{i}}}^{N}}$ | (9) |
Step 3 Establish the LONN model of the performance function with the random variables, train the LONN model with the selected training datasets. Compute the partial derivatives $\frac{\partial g}{\partial {{X}_{i}}}\left| _{x_{i}^{*}} \right.$ at the design point xi* through the successful trained LONN algorithm.
Step 4 Compute the partial derivatives $\frac{\partial g}{\partial {{X}_{i}}}\left| _{x_{i}^{*}} \right.$ in the equivalent standard normal space by the chain rule of differentiation as follows:
| $\frac{\partial g}{\partial {{X}_{i}}}\left| _{x_{i}^{*}} \right.=\left( \frac{\partial g}{\partial {{X}_{i}}}\left| _{x_{i}^{*}} \right. \right)\cdot \sigma _{{{X}_{i}}}^{N}$ | (10) |
Step 5 Compute the new values for the design point in the equivalent standard normal space using the following recursive formula:
| $\begin{align} & X_{k+1}^{'*}= \\ & \frac{1}{{{\left| \nabla g\left( X_{k}^{'*} \right) \right|}^{2}}}\left[ \nabla g{{\left( X_{k}^{'*} \right)}^{t}}X_{k}^{'*}-g\left( X_{k}^{'*} \right) \right]\nabla g\left( X_{k}^{'*} \right) \\ \end{align}$ | (11) |
where g(Xk'*) and ▽g(Xk'*) are, respectively, the values and the gradient vector of the limit state function at point Xk'* at the k-th iteration point. The subscript k refers to the iteration number.
Step 6 Compute the reliability index β and the new values for the design point in the original space:
| $\beta =\sqrt{\sum\limits_{i=1}^{n}{{{\left( x_{i}^{'*} \right)}^{2}}}}$ | (12) |
| $x_{i}^{*}=\mu _{{{X}_{i}}}^{N}+\sigma _{{{X}_{i}}}^{N}x_{i}^{'*}$ | (13) |
Step 7 Compute the value of the limit state function g(·) at the new design point xi*, and check the convergence criterion for |Δg(·)| and |Δβ| (in this paper the criterions are both less than 0.000 1). If both convergence criterions are satisfied, stop. Otherwise, repeat Steps 2-6 until convergence.
3 Numerical Examples 3.1 Cantilever Beam with Linear Elastic BehaviorThe reliability of a cantilever beam with a rectangular cross section, distributed uniform load and linear elastic behavior is analyzed [21]. The limit state function is defined as the maximum vertical displacement at the free end of the beam must not exceed the serviceability limit, which is l/325, where l is the length of the beam. Hence the performance function can be expressed by:
| ${{F}_{LS}}=\frac{l}{325}-\frac{wb{{l}^{4}}}{8EI}$ | (14) |
where E, w, I, b and l are the Young modulus, the intensity of the uniform load, the momentum of inertia, the width and the length of the beam, respectively. The material parameters are E=2.6×104 MPa and l=600 mm. Therefore, Eq.(14) is reduced to a function of two random variables and is given explicitly by:
| $0.01846154-74.76923\frac{{{X}_{1}}}{X_{2}^{3}}$ | (15) |
where X1 is the load w and X2 is the height h. The two variables have statistical characteristics given in Table 1 and are taken as non-correlated variables with a Gaussian probability distribution.
| Table 1 Statistical characteristics for cantilever beam variables |
The reliability of the cantilever beam is calculated with the proposed method. The LONN model has 2 input nodes, 8 hidden nodes, and 1 output node. As pointed out in the previous section, firstly, the training datasets for establishing the LONN are selected using the uniform design method. Secondly, the LONN with the selected data is established, and the approximate limit state function is determined by the well-trained LONN model. Finally, the FORM is used to predict the failure probability of the limit state function.The calculating result is β=2.337, which corresponds to a failure probability Pf=0.973 1×10-2. The results of the proposed method show good agreement with that of the MCS with importance sampling (exact value). Table 2 shows a result summary with different methods. Meanwhile, compared with the traditional BP-NN method, this method has the advantages of better accuracy, shorter computing time. BP-NN method consumes 215.047 3 seconds till reach the convergence accuracy, while the proposed method only takes 14.570 1 seconds to satisfy the convergence criterion (average values of 10 computing times). The most important advantage of the proposed method is that accurate results can be obtained even without using more training datasets.
| Table 2 Results summary for the example of the cantilever beam |
3.2 Fatigue Reliability Analysis on Loader Boom
Fig. 2 shows a wheel loader commonly used in the heavy construction industry. The loader boom as shown in Fig. 3 is the most important part, which is made of cast steel with deterministic elastic properties, as follows: Poisson's ratio ν=0.3, material density ρ=7.8×103kg/m3. Table 3 defines statistical properties which affect the fatigue life of the component. It is supposed the initial design life is 10 years. The objective is to predict fatigue reliability of the loader boom.

|
Figure 2 Wheel loader |

|
Figure 3 Loader boom |
| Table 3 Statistical properties of random inputs |
The work device is a symmetrical system, and the loads on the two booms are equal under symmetrical loads, therefore, only one loader boom is analyzed here. It calculates the internal forces on the loader boom under each working condition in one working cycle with analytical method.
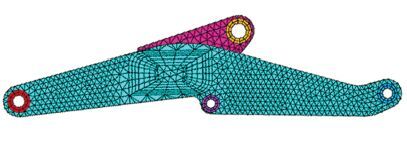
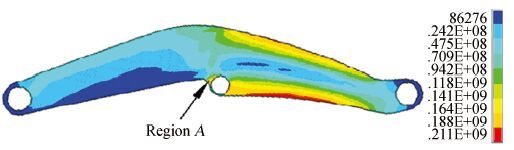
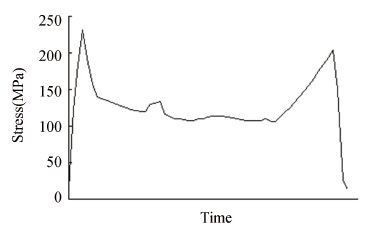
It analyzes the stress and strain condition on the structure with FEM. Fig. 4 shows the finite-element mesh model of the loader boom which is generated with ANSYS software. Then the equivalent stress and strains will be obtained under the internal force of the whole working process. The analysis results show the stress contour of the loader boom (as shown in Fig. 5), in Region A where there is the largest stress, which take place during the shoveling process of the loader. The stress-time history and strain-time history of loader boom at the critical point can be obtained simultaneously, which are shown in Figs. 6 and 7.
|
Figure 4 Mesh model |
|
Figure 5 Stress contour of the model |

|
Figure 6 Local strain history |
|
Figure 7 Local stress history |
With rainflow algorithm[22], the stress-time history and strain-time history are schematized. Two full cycles are obtained in one working cycle. Then the mean stress and strain amplitude of each cycle can be calculated. It calculates the crack initiation life and damage corresponding to each cycle at the critical point with Coffin-Manson-Morrow equation[22], and the fatigue life will be obtained according to Miner linear cumulative damage theory. The fatigue crack-initiation life Nf can be defined as:
| ${{\varepsilon }_{a}}=\frac{\left( \sigma _{f}^{'}-{{\sigma }_{m}} \right)}{E}{{\left( 2{{N}_{f}} \right)}^{b}}+\varepsilon _{f}^{'}{{\left( 2{{N}_{f}} \right)}^{c}}$ | (16) |
where σf' is fatigue strength coefficient; b is fatigue strength exponent; εf' is fatigue ductility coefficient, and c is fatigue ductility exponent; E is Young's modulus, which are all material properties and considered random variables; εa is the equivalent strain amplitude and σm is the equivalent mean stress, both of which depend on strain and stress fields obtained previously.
The performance function of the loader boom can be defined as
| $\begin{align} & {{F}_{LS}}=g\left( \sigma _{f}^{'}, b, \varepsilon _{f}^{'}, c, E \right)= \\ & {{N}_{f}}\left( \sigma _{f}^{'}, b, \varepsilon _{f}^{'}, c, E \right)-{{N}_{D}} \\ \end{align}$ | (17) |
where ND is the initial design life, ND=10 years.
It calculates the fatigue reliability of the critical point with the proposed method. It is supposed that the loader works 8 hours a day for 360 working days each year, and it takes 11.8 seconds for the loader machine to complete a whole working cycle. Then if the design life is 10 years, it calculates the fatigue reliability according to LONN-RSM demonstrated in Section 2.3 step by step, and will obtain these results: reliability index is β=3.248 1, and the equivalent reliability will be 99.80%. The result shows that the developed method can be used to analyze structural reliability with highly non-linear performance functions.
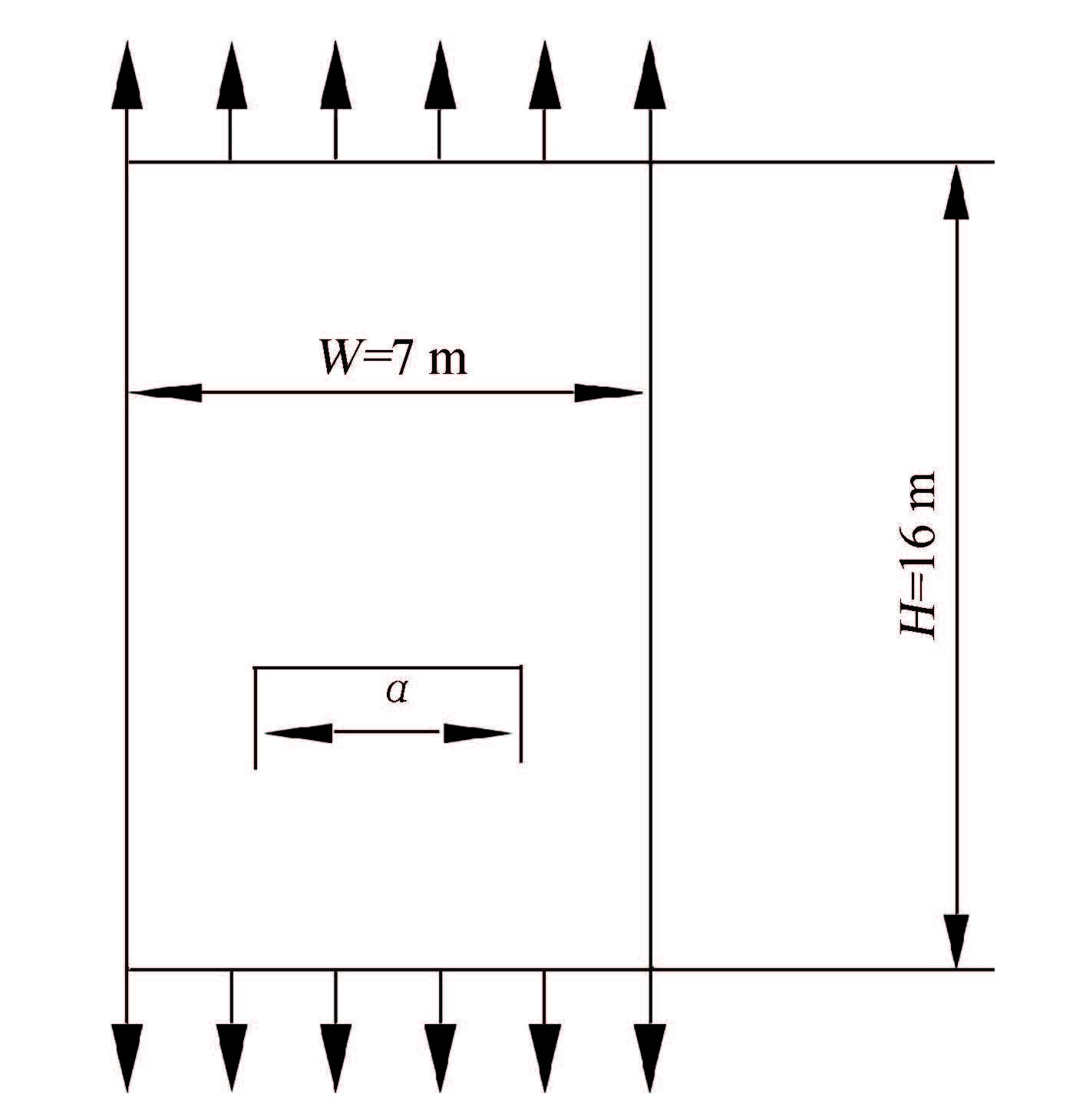
3.3 Thin Plate with a Center CrackThe third example deals with the reliability analysis of a structure with implicit performance function, a rectangular thin plate with a center crack is analyzed, which is subjected to uniformed tensile stress at both ends rectangular to the crack. The sample is assumed to be isotropic and under plane strain condition. The geometrical parameters are shown in Fig. 8, which are assumed to be deterministic, and the material parameters are Young's modulus E=2.10 GPa, Poisson's ratio ν=0.25. The limit state function is defined implicitly by:
| ${{F}_{LS}}=g\left( {{K}_{IC}}, a, \sigma \right)={{K}_{IC}}-{{K}_{1}}\left( a, \sigma \right)$ | (18) |
|
Figure 8 Thin plate with center crack |
where KIC is the fracture toughness of the material, which is the critical value of the stress intensity factor KI at which the crack begin to propagation under static load; a is the length of the center crack and σ is the loaded stress. These three variables have statistical characteristics given in Table 4 and are taken as non-correlated variables with Gaussian probability distribution.
| Table 4 Statistical characteristics for the fracture plate variables |
The stress intensity factor KI at the crack tip is analyzed with FEM, and one-quarter model is used because of symmetry, and the established FEM model is shown in Fig. 9.

|
Figure 9 FEM model |
The performance function of the structure is defined as Eq.(18), and the random variables which affect the reliability of the structure are KIC, σ and a. Meanwhile the stress intensity factor KI is an implicit function of parameter σ and a, the LONN model is used to simulate the relationship of the performance function and the three parameters, and establish a three layer LONN. The input layer is {KIC, σ, a, } and the output is theperformance function g(·), and the processing elements in the hidden layer are 27 Legendre polynomials, and the LONN will be successfully trained and the weights will be extracted, thus an explicit performance function can be obtained. The LONN model is then connected to FORM reliability method to predict the failure probability. According to the calculation steps, the analytical solution for this example is obtained after six iterations. The final checking points is (3.879 63, 28.658 56, 133.682 13), and the reliability index is β=2.666 26. The result shows that the proposed approach is applicable to structural reliability analysis involving implicit performance functions.
4 ConclusionA new LONN-based RSM is developed for predicting failure probability of structures, in the case of limit states involving highly non-linear and implicit performance functions. The LONN is applied in the method to simultaneously estimate the structural performance function and its partial derivatives. Three numerical examples involving mathematical functions and structural problems are used to illustrate the proposed method. Comparisons are made with alternative approximate and simulation methods to evaluate the accuracy and computational efficiency of the method developed. Numerical results indicate that the proposed method provides accurate and computationally efficient estimates of probability of failure. The examples show that the proposed approach is applicable to structural reliability analysis involving implicit performance functions, as well as highly non-linear performance functions, the developed method offered great potential for structural reliability.
| [1] |
Zhang M.
Structural reliability analysis:methods and procedures. Beijing: Science Press, 2009 .
( 0) 0)
|
| [2] |
Gong J X, Zhao G F. Applications and developments of structural reliability theory abroad.
China Civil Engineering Journal,2005, 38 (2) : 1-7.
( 0) 0)
|
| [3] |
Elsayed E A.
Reliability engineering. Beijing: Electronic Industry Press, 2013 .
( 0) 0)
|
| [4] |
Faravelli L. Response surface approach for reliability analysis.
Journal of Engineering Mechanics,1989, 115 (12) : 2763-2781.
( 0) 0)
|
| [5] |
Guan X L, Melchers R E. Effect of response surface parameter variation on structural reliability estimates.
Structural Safety,2001, 23 (4) : 429-444.
( 0) 0)
|
| [6] |
Basaga H B, Bayraktar A, Kaymaz I. An improved response surface method for reliability analysis of structures.
Structural Engineering and Mechanics,2012, 42 (2) : 175-189.
( 0) 0)
|
| [7] |
Xing H J, Ha M H.
Feed-forward neural network and applications. Beijing: Science Press, 2013 .
( 0) 0)
|
| [8] |
Scarselli F, Tsoi A C. Universal approximation using feedforward neural networks:a survey of some existing methods, and some new results.
Neural Networks,1998, 1 (11) : 15-37.
( 0) 0)
|
| [9] |
Gomes H M, Awruch A M. Comparison of response surface and neural network with other methods for structural reliability analysis.
Structural Safety,2004, 26 (1) : 49-67.
( 0) 0)
|
| [10] |
Li G B, Meng G W, Li F, et al. A new response surface method for structural reliability analysis.
Advanced Materials Research,2013, 712 : 1506-1509.
( 0) 0)
|
| [11] |
Deng J, Yue Z Q, Tham L G, et al. Pillar design by combining finite element methods , neural networks and reliability : a case study of the Feng Huangshan copper mine, China.
International Journal of Rock Mechanics and Mining Sciences,2003, 40 (4) : 585-599.
( 0) 0)
|
| [12] |
Cheng J, Li Q S, Xiao R C. A new artificial neural network-based response surface method for structural reliability analysis.
Probabilistic Engineering Mechanics,2008, 23 (1) : 51-63.
( 0) 0)
|
| [13] |
Snehamoy C, Sukumar B. Reliability estimation using a genetic algorithm-based artificial neural network: an application to a load-haul-dump machine.
Expert Systems with Applications,2012, 39 : 10943-10951.
( 0) 0)
|
| [14] |
Qian S, Lee Y C, Jones R D, et al. Function approximation with an orthogonal basis net.
International Joint Conference on Neural Networks,1990, 3 : 605-618.
( 0) 0)
|
| [15] |
Zou A J, Zhang Y N.
Basis function neural networks and applications. Guangzhou: Sun Yat-sen University Press, 2009 .
( 0) 0)
|
| [16] |
Jiang A M, Zhang Y Z.
Computing methods. Beijing: Science Press, 2004 .
( 0) 0)
|
| [17] |
Department of Computational Mathematics, Tongji University.
Advanced numerical computing. Beijing: The people's Posts and Telecommunications Press, 2009 .
( 0) 0)
|
| [18] |
Sher C F, Tseng C S, Chen C S. Properties and performance of orthogonal neural network in function approximation.
Int J Intekk Syst,2001, 16 (12) : 1377-1392.
( 0) 0)
|
| [19] |
Yang S S, Tseng C S. An orthogonal neural network for function approximation.
IEEE Transactions on System, Man and Cybernetics,1996, 26 (5) : 779-784.
( 0) 0)
|
| [20] |
Elhewy A H, Mesbahi E, Pu Y. Reliability analysis of structures using neural network method.
Probabilistic Engineering Mechanics,2006, 21 (1) : 44-53.
( 0) 0)
|
| [21] |
Gomes H M, Awruch A M. Comparison of response surface and neural network with other methods for structural reliability analysis.
Structural Safety,2004, 26 (1) : 49-67.
( 0) 0)
|
| [22] |
Yao W X.
Fatigue Life Prediction of Structures. Beijing: Defence Industrial Press, 2003 .
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


