2. Transportation Research Center, School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
In urban transit system, scheduled-based strategy is often used to monitor and adjust bus operation. The schedule usually includes a series of time points and respective scheduled arrival and departure time. With the real-time information about scheduled deviation at previous time point, bus drivers can adjust bus speed and catch up the scheduled arrived time at next time point[1]. The scheduled arrived time is calculated based on the scheduled travel time between two adjacent time points. As a result, bus drivers would regard it as the guide to adjust the bus operation speed[2] and improve service punctuality.
Generally, operators insert particular amounts of slack time into the mean travel time (MTT) to derive the scheduled travel time for the segment between two consecutive time points. Thus, determining appropriate slack time is the key point for scheduled travel time setting. However, in reality, operators usually set slack time based on their own experiences. Consequently, drivers might be misguided under certain situations and bring some inconvenience to passengers. Therefore, operators need to set the scheduled travel time to match the real-world condition and minimize the risk of scheduled deviation.
In the literatures, scheduled travel time was determined by analyzing time randomness in different time bands[3]. In addition, many studies considered holding strategy for scheduled time optimization[4-8]. However, holding strategy could annoy passengers because no passengers would like to sit at stop even if they are ahead of schedule[1]. Moreover, drivers’ adjustment effort, an important aspect in transit operation[9-10], was generally neglected. To remedy this problem, Yan et al.[2] considered the driver adjustment factor and proposed a robust optimization model for setting scheduled time without holding strategy. Zhao et al.[11] improved the optimization model in a spatially equal way. In their studies, Monte Carlo (MC) simulation was used to generate Lognormal-distributed travel time samples to calculate the optimal slack time. However, the unimodal distribution could not well explain different service states and travel time variability, so more calibration work, especially for the actual travel time distribution, was necessary for determining scheduled travel time. Meanwhile, since multistate distribution model is able to represent the characteristics of different states, it significantly improves model fitting[12-15] compared with unimodal model. Therefore, in this paper we used multistate model to replace traditional distribution model for statistical analysis and MC simulation.
The aim of this paper is to model travel time distribution and set segment scheduled travel time to minimize scheduled deviation. Firstly, we use multistate model to fit collected data, and provide the calibrated parameters for simulation-based optimization. Then, an optimization model is proposed for setting optimal slack time for each segment, followed by a MCS-GA (Monte Carlo simulation based genetic algorithm) solution procedure. The sensitivity analysis reveals that the results can not only provide the requirement to improve reliability for drivers, but also offer an important guideline for schedule design and reliability analysis.
2 MethodologyConsidering a fixed bus route with S bus stops and n time points, all of the time points are predetermined at major trip generation locations. The first bus stop is indexed as the time point 1 and last stop is the time point n. To reflect the actual travel time variability, we classify the travel time distribution into multiple groups, and each group represents a transit service state. For a given segment, the actual travel time under each state is assumed to a continuous random variable following a specified probability density function (PDF). Occurrence probability of service state and corresponding PDF are estimated from historical GPS data recorded under unscheduled condition.
2.1 Multistate ModelMultistate model is a mixed distribution model comprising a number of component functions. If each component follows a normal distribution, multistate model can be expressed as a Gaussian Mixed Model (GMM). In modeling travel time distribution, multistate model outperforms other single-mode models as it is able to cluster data into groups with a given probability[12]. Furthermore, multistate model not only reflects the state occurrence probabilities, but also provides the travel time probability density function (PDF) under each state. The density function of multistate model with K components is described as follows:
| $f\left( T{{T}_{i-1, i}}\left| w, \theta \right. \right)=\sum\limits_{k=1}^{k}{{{w}_{k}}}\left( T{{T}_{i-1, i}}\left| \theta \right. \right)$ | (1) |
where TTi-1, i is the actual travel time from time point i-1 to i; w=(w1, …, wK) is the vector of mixture coefficients; θ=(θ1, …, θK) is the vector of model parameters for each component distribution; θk is the vector of model parameters for component k, fk (TTi-1, i |θk) is the probability density function for component k.
In particular, the mixture coefficient wk in Eq.(1) is interpreted as the probability that state k occurs, and fk (TTi-1, i|θk) indicates the corresponding travel time distribution. This connection provides the function for analyzing travel time reliability and optimal slack time. A special case of the multistate model is a two-component normal distribution:
| $\begin{align} & w\frac{1}{\sqrt{2\pi {{\sigma }_{1}}}}\exp \left\{ -\frac{1}{2\sigma _{1}^{2}}{{\left( T{{T}_{i-1, i}}\left| {{u}_{1}} \right. \right)}^{2}} \right\}+ \\ & \left( 1-w \right)\frac{1}{\sqrt{2\pi {{\sigma }_{2}}}}\exp \left\{ -\frac{1}{2\sigma _{2}^{2}}{{\left( T{{T}_{i-1, i}}\left| {{u}_{2}} \right. \right)}^{2}} \right\} \\ \end{align}$ | (2) |
where w and 1-w is the occurrence probability for each state; μk and σk is the mean and standard variance of kth normal distribution respectively.
Expectation and Maximization (EM)algorithm[14] is applied to estimate the parameters of multistate model, including the number of states and other statistical parameters. Akaike Information Criterion (AIC) is used to evaluate the model performance in fitting collected data[16]. The AIC is defined as:
| $AIC=2P-2\ln \left( L\left( {{\theta }_{\text{MIE}}} \right) \right)$ | (3) |
where L(θMLE) is the maximum likelihood function; P is the number of model parameters. The first term value avoids excessive model complexity while the second term measures the goodness of model fitting. A smaller AIC indicates a preferred model with certain number of states. In general, complicated models will fit real data better than simple models. However, extra model complexity may outweigh the benefits in model fitting due to excessive calibrations and poor interpretability. Therefore, AIC considers goodness-of-fit for data and model complexity simultaneously, providing a balanced model assessment index. Furthermore, if AIC gap between two models is more than 4, the two models are significantly different from each other[17].
2.2 Scheduled Travel Time ModelIn existing studies[2, 11], the allocated slack time is independent of transit service states, which consequently cannot reflected the travel time variability between service states. To remedy this problem, we firstly compute the slack time for each state respectively, and then aggregate all based on respective occurrence probability. For service state k, TTk(x) is defined as the xth percentile of travel time distribution. The slack time under service state k is listed as follows:
| $T{{T}^{k}}\left( x \right)=F_{k}^{-1}\left( x \right)$ | (4) |
| $ST_{i-1, i}^{k}\left( x \right)=\left\{ \begin{matrix} T{{T}^{k}}\left( x \right)-MT{{T}_{i-1, i}}, & ST_{i-1, i}^{k}\left( x \right)\ge MT{{T}_{i-1, i}} \\ \text{0, } & \text{Otherwise} \\ \end{matrix} \right.$ | (5) |
where Fk-1(x) denotes the inverse distribution of travel time cumulative distribution function (CDF) for fk (TTi-1, i |θk) in Eq.(1) ; TTki-1, i(x) is the travel time at level x under state k from time point i-1 to i; MTTi-1, i is the mean travel time and represents the travel time expectation of transit operators; STi-1, ik(x) is the difference between TTi-1, ik(x) and MTTi-1, i. By nature of the slack time, it can be regarded as the time budget for service unreliability under each state and its value should be no less than zero.
Using x as the slack time level, we proposed the concept of expected slack time (EST), which is defined as the occurrence probability weighted value under different states and formulated as:
| $ES{{T}_{i-1, i}}=\sum\limits_{k=1}^{k}{{{w}_{k}}}\times ST_{i-1, i}^{k}\left( x \right)$ | (6) |
where ESTi-1, i is the expected value of slack time under different states from time point i-1 to i; STki-1, i(x) is the slack time at level k under state k; wk is the mixture coefficient in Eq.(1) and represents the occurrence probability of service state k. In modeling EST, the slack time for different service states are aggregated based on their occurrence probabilities. For example, non-recurrent congestion can cause the highest slack time, but if it rarely happens, its contribution to the EST is very limited. Based on mean travel time MTTi-1, i, the scheduled travel time STTi-1, i is defined as:
| $ST{{T}_{i-1, i}}=MT{{T}_{i-1, i}}+ES{{T}_{i-1, i}}$ | (7) |
With Eq.(6) , the scheduled deviation SDi at time point i is formulated as:
| $\begin{align} & S{{D}_{i}}=\left( ST{{T}_{i-1, i}}-T{{T}_{i-1, i}} \right)+\left( 1-{{\beta }_{i-1, i}} \right)S{{D}_{i-1}}= \\ & \left( MT{{T}_{i-1, i}}+ES{{T}_{i-1, i}}-MT{{T}_{i-1, i}}+ES{{T}_{i-1, i}} \right)+ \\ & \left( 1-{{\beta }_{i-1, i}} \right)S{{D}_{i-1}} \\ \end{align}$ | (8) |
where STTi-1, i is the scheduled travel time from time point i-1 to i; TTi-1, i is the actual travel time; βi-1, i is the adjustment factor for the segment, which is assumed to uniformly be distributed in the specified interval. We assume that drivers’ adjustment efforts are only effective without road congestion. In reality, the value of adjustment factor should be calibrated with more travel time data under schedule manner. Generally, no delay will occur when bus departs from the starting station and drivers do not make any adjustments in the first segment, so driver adjustment factor equals to zero in the first segment.
Based on operator’s attitudes about earlier and late arrivals, generalized schedule deviation GSDi is defined as the weighted difference between scheduled travel time and actual travel time from time point i-1 to i, and it can also be regarded as the matching of scheduled time and actual travel time.
| $GS{{D}_{i}}={{\rho }_{1}}\max \left( S{{D}_{i}}, 0 \right)+{{\rho }_{2}}\max \left( -S{{D}_{i}}, 0 \right)$ | (9) |
where ρ1 and ρ2 are two coefficients representing the penalty of earlier and late arrivals at the time points. If transit operators assume that earlier arrivals are more harmful than late arrivals (ρ2/ρ1 <1) , the scheduled travel time is close to MTT for each segment. In contrast, the larger penalty ratio ρ2/ρ1 is, the more harmful later arrivals are assumed to be transit operators. To determine the optimal slack level x for each segment, an optimization model is formulated as:
| $z\left( x \right)=\min \sum\limits_{i=2}^{N}{E}\left[ GSD{{\left( {{x}_{i}} \right)}_{i}} \right]$ | (10) |
subject to
| $\sum\limits_{i=2}^{N}{E}S{{T}_{i-1, i}} <\frac{hN}{2}-C$ | (11) |
| ${{x}_{\min }}\le {{x}_{i}}\le {{x}_{\max }}$ | (12) |
where x=(xi, i = 2, …, n) is the vector of slack time level for each segment; h is the scheduled headway; N is the number of buses deployed in the route, and C is the half-cycle operation time.
In the model, the objective function in Eq.(10) is to minimize the sum of expected scheduled deviation in all segments. As multiple bus runs can result in different scheduled deviation, we use the expected value of GSD to reflect the difference between actual travel time and scheduled travel time. The constraint in Eq.(11) implies that the amount of allocated slack time should not be too large, so that operators can set recovery time for drivers at terminal station[8]. The constraint in Eq.(12) defines the lower and upper bounds of slack time level.
2.3 Solution AlgorithmAs the objective function in Eq.(10) is involved with the expected value term and it does not have a closed form, Genetic Algorithm (GA) is applied for solving the model formulated by Eqs.(10) -(12) . Meanwhile, since expected value of GSDi needs larger random sample size than existing data set, we use Monte Carlo (MC) simulation to generate random samples for travel time and adjustment factor. Thus, Monte Carlo simulation based Genetic Algorithm (MCS-GA) is introduced to solve the proposed scheduled travel time setting problem.
In generating multistate-distributed travel time samples, we firstly estimate the number of samples falling into each state and then generate the specific travel time values based on certain normal distribution. With MC simulation, M realizations of random variables (TT(m)i-1, i, β(m)i-1, i) i = 2, …, n are generated for slack time calculation based on calibration results. The expected value in the objective function can be approximated by the sample mean based on GSDi.
| $E\left[ GSD{{\left( {{x}_{i}} \right)}_{i}} \right]\approx \frac{1}{M}\sum\limits_{m=1}^{M}{G}SD_{i}^{\left( m \right)}\left( {{x}_{i}}, TT_{i-1, i}^{\left( m \right)}, \beta _{i-1, i}^{\left( m \right)}, {{\rho }_{1}}, {{\rho }_{2}} \right)$ | (13) |
In the GA procedure[18], a feasible solution is coded into one chromosome using binary integer strings. To evaluate the fitness of a chromosome, the penalty method is introduced in order to handle the constraint Eq.(10) . The modified objective function is defined as:
| $\begin{align} & \bar{z}\left( x \right)=\sum\limits_{i=2}^{n}{E}\left[ GSD{{\left( {{x}_{i}} \right)}_{i}} \right]+ \\ & \eta \max \left[ \sum\limits_{i=2}^{n}{ES{{T}_{i-1, i}}-\left( \frac{hN}{2}-C \right), 0} \right] \\ \end{align}$ | (14) |
where η is the penalty associated with the constraint Eq.(11) .
With the modified objective function, the fitness value can be obtained for each chromosome. The GA procedures continue iteratively until the convergence or predefined maximal iteration number is attained. The entire MCS-GA procedure is summarized as follows:
Step 1 Generate the starting population and define the initial parameters, including population size, the maximal number of generation Nmax, the number of realizations M, cross rate and mutation rate. The generation N is set to be 0.
Step 2 Generate M samples of travel time and adjustment factors: (TTi-1, i(m), βi-1, i(m)) i = 2, 3, …, n using Monte Carlo simulation technique based on multistate distribution and uniform distribution respectively.
Step 3 Calculate the fitness function for each chromosome; improve the solution by taking the reproduce, crossover, and mutation procedures, then N=N+1.
Step 4 If N>Nmax, the evolution is terminated and then output the optimal slack time level x for each segment. Otherwise, go to Step 3 for the next iteration.
3 Numerical ExamplesTaking the westbound direction of Route 201 in Shenzhen, China as a case study to demonstrate the model effectiveness. Locations of time points are mainly set to the stops near major trip generation zones, such as school and shopping centers. Considering the travel time variability in peak hours, we use the GPS bus data during 7:00-9:00, from Oct. 14 to Nov. 1, 2013, to set the slack time for each segment. The time points setting and MTT for each segment is presented in Table 1, which indicates that mean trip time for westbound route during peak hours is 89 minutes. The number of deployed buses is 40 and the scheduled headway is 5 min. According to Eq.(11) , the total allocated slack time is 11 minutes.
As computed by EM algorithm, different numbers of service states are classified from historical data. We use Lognormal distribution as the benchmark to test the benefits of multistate model, because Lognormal model well represents the right tail of travel time distribution compared with other unimodal models [19-20]. Since the travel time distribution is expected to vary with time of day, we also use those models to fit the data during off-peak hours (14:00-16:00) for comparison. As indicated in Section 2.1, AIC is used to measure the model performance and a smaller AIC indicates a preferred model. Table 2 presents AIC of Lognormal and multistate model with different number of components, in which optimal model is marked in bold front. Since the service states in peak hours are unstable, multistate model with three or four states consistently outperforms Lognormal distribution. However, there are fewer states for each segment at off-peak hours, and the advantage from multistate model narrows. Although Lognormal distribution is better than multistate model in Seg. 2 during off-peak hours, the difference is not statistically significant (AIC difference less than 4[17]). Overall, multistate model is able to generate a good fitting for real data without too much model complexity.
| Table 1 Time points setting and MTT between two consecutive time points during peak hours |
| Table 2 Model comparison based Akaike Information Criterion (AIC) |
In Fig. 1, travel time data in Segs.1 and 2 during peak hours are taken as examples to show the difference in goodness-of-fit between Lognormal and multistate model. It can be figured that multistate model fits the data histogram closely, while Lognormal distribution shows a lack of fit. For Seg.1, the definition of three service states can be interpreted as: fast, slow and non-recurrent. Fluctuations on traffic volume and passenger demand contribute to different service states in recurrent condition[21], while accidents on road may cause non-recurrent state[13]. For four-state model, it is interpreted that there is one more service state in the recurrent condition (Fig. 1 (b)). It is multistate model that captures characteristics of data during peak hours and thus shows a better data fitting compared with Lognormal distribution.
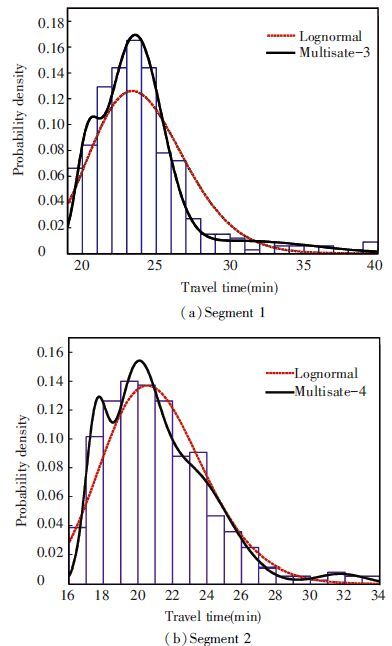
|
Figure 1 Comparison between Lognormal model and multistate model for fitting data during peak hours |
Based on the optimal model calibration results presented in Table 3, we apply MC simulation technique to generate multistate-distributed travel time samples during peak hours. For drivers’ adjustment factor, it is observed that the average adjustment factors are mostly between -0.5 and 0.5[10]. However, if transit schedule is preset, drivers will react to it and recover deviation, and the adjustment factor should be larger than zero. Since drivers can hardly make adjustments in the congested condition, it is assumed that their recovery efforts are only effective when buses are operated in a relatively free traffic flow (i.e. State 1 for three-state model or States 1 and 2 for four-state model); that is, if the travel time belongs to those states, the corresponding adjustment factor is set to be uniformly distributed in the interval [0, 0.5], otherwise it is equal to zero.
In this study, the upper and lower bounds of slack level x are set to be 0.1 and 99.9, respectively. The GA parameters are set as follows: the population size is 100; the maximum number for generation is 100; the crossover rate is 0.8; and the mutation rate is 0.05. The sample size M is set to be 1 000 and penalty ratio ρ2/ρ1 is 2. The computational results are presented in Table 4. For more details about parameters setting, see Gen et al[18].
Although setting scheduled travel time cannot improve service reliability directly like holding strategy, it provides bus drivers the guideline to adjust bus speed and guarantee punctuality. Therefore, the amount of allocated slack time should be consistent with travel time reliability of the segment. In previous works[22-23], buffer time was often defined as the measurement for travel time reliability, which was the difference between 95th percentage travel time and mean travel time. However, it cannot distinguish the influence from different service states[24]. Therefore, we use the concept of expected reliability buffer time index (EBTI) to measure the service reliability:
| $\begin{align} & EB{{T}_{i-1, i}}=\sum\limits_{k=1}^{k}{{{w}_{k}}}\times ST_{i-1, i}^{k}\left( 95 \right) \\ & EBT{{I}_{i-1, i}}=EB{{T}_{i-1, i}}/MT{{T}_{i-1, i}} \\ \end{align}$ |
The larger EBTi-1, i and EBTIi-1, i means lower level of travel time reliability because passengers and operators may allocate more buffer time for late arrivals. The EBTI for each segment is presented in Table 4.
| Table 3 Calibration results of multistate model for all segments during peak hours |
| Table 4 Computational results on the EST and EBTI during peak hours |
The results show that the allocated slack time level/EST basically reflects the travel time reliability in each segment. Specifically, the segments with higher EBTI need more slack time compared with the segments with lower one. In Table 4, slack time levels of Segs.1-3 are more twice than Seg.4. The reason for the difference is that Seg.4 has the highest travel time reliability (EBTI=0.12) among all segments. Therefore, the optimal EST can be seen as the requirement for bus drivers to improve reliability and minimize scheduled deviation.
To explore the relationship between slack time level and operator’s attitude towards earlier and late arrivals, EST values under different penalty ratio ρ2/ρ1 are plotted in Fig. 2. Generally, the expected slack time tends to increase with ρ2/ρ1, which means operators need more slack time to avoid late arrivals. Furthermore, for the segments with lower travel time reliability (Segs.1-3) , the EST is more sensitive to operators’ risk preference than the one with higher reliability (Seg.4) . It is indicated that the slack time should be determined with more reference to operator’s attitude in those segments with unreliable travel time. On the contrary, operators’ attitude has no obvious influence on the segments with high travel time reliability. Although there is no clear conclusion about the value of penalty ratio in previous studies[2, 4, 11], ρ2/ρ1 is suggested to be larger than 1 to provide a positive slack time value for peak hours.
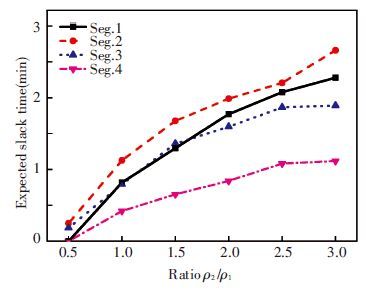
|
Figure 2 Expected slack time for each segment during peak hours based on different ratio ρ2/ρ1 |
Fig. 3 depicts the expected slack time based on different numbers of deployed buses. Given the fixed bus frequency, the number of deployed buses determines the total amount of allocated expected slack time with Eq. (11) . With the increase in number of deployed buses, each segment is expected to get more slack time until bus number does not restrict the total amount of slack time. Even if the bus number is low (less than 38) , it is found that Segs.1 and 2 still should be allocated more than 1-minute expected slack time to guarantee service level, which means that segments with low travel time reliability have the priority to get slack time. In contrast, Seg.4 constantly gets the least slack time among all segments. It is a desirable result because Seg.4 has the highest travel time reliability during peak hours.
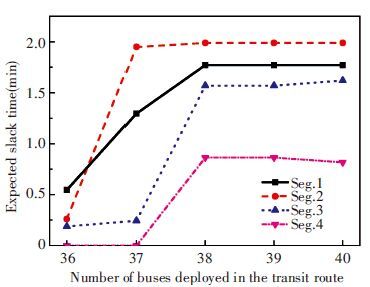
|
Figure 3 Expected slack time for each segment during peak hours based on different number of deployed buses |
4 Conclusions
In transit operation, the determination of scheduled travel time is important for transit operators to design schedule and monitor system performance[25]. This study further investigates the scheduled travel time setting based on multistate model. Lognormal distribution and multistate model are used to fit historical travel time data for comparison. With the calibrated parameters, MC technique generates multistate-distributed travel time samples. Subsequently, an optimization model is proposed and the GA solution method is used to find the optimal slack time level. Sensitivity analysis is conducted to study the effects of penalty ratio and the number of deployed buses on slack time setting.
Several findings are obtained as follows: firstly, multistate model generates better performance compared with Lognormal distribution during peak hours, although the benefit of multistate model is limited at off-peak hours. With the Monte Carlo Simulation technique, multistate-distributed travel time samples are able to represent different service states during peak hours. Then, the optimal slack time is found to be consistent with the segment travel time reliability, so it can be regarded as a requirement for drivers to minimize scheduled deviation. Finally, EST values in the segments with low travel time reliability are sensitive to operators’ risk preference, and those segments have the priority to obtain slack time with the variance of deployed bus numbers.
In this study, there are still some limitations and future research can be done in following directions. For example, as travel time data are recorded under unscheduled condition, more observations and calibrations on driver’s adjustment behaviors are needed in future studies. Then, multistate model with skewed component should be investigated further. The value of penalty ratio should be determined with more surveys on operators’ risk preference.
| [1] |
Ji Y, He L, Zhang H M. Bus drivers´ responses to real-time schedule adherence and their effects on transit reliability. Proceedings of Transportation Research Board. Washington DC: National Academy of Sciences, 2014.
( 0) 0)
|
| [2] |
Yan Y, Meng Q, Wang S, et al. Robust optimization model of schedule design for a fixed bus route.
Transportation Research Part C: Emerging Technologies,2012, 25 : 113-121.
( 0) 0)
|
| [3] |
Dessouky M, Hall R, Nowroozi A, et al. Bus dispatching at timed transfer transit stations using bus tracking technology.
Transportation Research Part C: Emerging Technologies,1999, 7 (4) : 187-208.
( 0) 0)
|
| [4] |
Salicrú M, Fleurent C, Armengol J M. Timetable-based operation in urban transport: run-time optimization and improvements in the operating process.
Transportation Research Part A: Policy and Practice,2011, 45 (8) : 721-740.
( 0) 0)
|
| [5] |
Sun D J, Elefteriadou L. Lane changing behavior on urban street: an “in-vehicle” field experiment based study.
Computer-Aided Civil and Infrastructure Engineering,2012, 27 (7) : 525-542.
( 0) 0)
|
| [6] |
Zhao J, Dessouky M, Bukkapatnam S. Optimal slack time for schedule-based transit operations.
Transportation Science,2006, 40 (4) : 529-539.
( 0) 0)
|
| [7] |
Furth P G, Muller T H J. Optimality conditions for public transport schedules with timepoint holding.
Public Transport,2009, 1 (2) : 87-102.
( 0) 0)
|
| [8] |
Liu G, Wirasinghe S C. A simulation model of reliable schedule design for a fixed transit route.
Journal of Advanced Transportation,2001, 35 (2) : 145-174.
( 0) 0)
|
| [9] |
Lin W H, Bertini R L. Modeling schedule recovery processes in transit operations for bus arrival time prediction.
Journal of Advanced Transportation,2004, 38 (3) : 347-365.
( 0) 0)
|
| [10] |
Chen M, Liu X B, Xia J X. Dynamic prediction method with schedule recovery impact for bus arrival time.
Transportation Research Record: Journal of the Transportation Research Board,2005, 1923 : 208-217.
( 0) 0)
|
| [11] |
Zhao H, Zhang C, Gao Z, et al. Risk-based transit schedule design for a fixed route from the view of equity.
Journal of Transportation Engineering,2013, 139 (11) : 1086-1094.
( 0) 0)
|
| [12] |
Guo F, Rakha H, Park S. Multistate model for travel time reliability.
Transportation Research Record: Journal of the Transportation Research Board,2010, 2188 : 46-54.
( 0) 0)
|
| [13] |
Barkley T, Hranac R, Petty K. Relating travel time reliability and nonrecurrent congestion with multistate models.
Transportation Research Record: Journal of the Transportation Research Board,2012, 2278 : 13-20.
( 0) 0)
|
| [14] |
Arcidiacono P, Jones J B. Finite mixture distributions, sequential likelihood and the EM algorithm.
Econometrica,2003, 71 (3) : 933-946.
( 0) 0)
|
| [15] |
Sun D J, Elefteriadou L. Research and implementation of lane-changing model based on driver behavior.
Transportation Research Record: Journal of the Transportation Research Board,2010, 2161 : 1-10.
( 0) 0)
|
| [16] |
Akaike H. A new look at the statistical model identification.
IEEE Transactions on Automatic Control,1974, 19 (6) : 716-723.
( 0) 0)
|
| [17] |
Burnham K P, Anderson D R.
Model Selection and Multi-model Inference: A Practical Information-theoretic Approach. Berlin: Springer, 2002 .
( 0) 0)
|
| [18] |
Gen M, Cheng R. Genetic Algorithms and Engineering Optimization. New York: Wiley, 1999.
( 0) 0)
|
| [19] |
Mazloumi E, Currie G, Rose G. Using GPS data to gain insight into public transport travel time variability.
Journal of Transportation Engineering,2010, 136 (7) : 623-631.
( 0) 0)
|
| [20] |
Kieu L M, Bhaskar A, Chung E. Establishing definitions and modeling public transport travel time variability. Proceedings of Transportation Research Board. Washington DC: National Academy of Sciences, 2014.
( 0) 0)
|
| [21] |
Xue R, Sun, D J, Chen S. Short-term bus passenger demand prediction based on time series model and interactive multiple model approach. Discrete Dynamics in Nature and Society, 2015, Article ID: 682390.
( 0) 0)
|
| [22] |
Sun D J, Kondyli A. Modeling vehicle interactions during lane-changing behavior on arterial streets.
Computer-Aided Civil and Infrastructure Engineering,2010, 25 (8) : 557-571.
( 0) 0)
|
| [23] |
Yan Y, Guo X, Li Y, et al. Bus transit travel time reliability evaluation based on automatic vehicle location data.
Journal of Southeast University (English Edition),2012, 28 (1) : 100-105.
( 0) 0)
|
| [24] |
Ma Z, Ferreira L, Mesbah M. Measuring service reliability using automatic vehicle location data. Mathematical Problems in Engineering, 2014, Article ID 468563, 12.
( 0) 0)
|
| [25] |
Sun D J, Xu Y, Peng Z R. Timetable optimization for single bus line based on hybrid vehicle size model. Journal of Traffic and Transportation Engineering (English Edition), 2015, doi:10.1016/j.jtte.2015.03.006.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


