2. School of Information Science and Engineering, Central South University, Changsha 410083, China
With the development of economy and society, more and more enterprises tend to form coalitions to jointly operate. Coalition members usually have a common goal in the transverse and longitudinal industry chain. More and more attentions are paid by theory and business circles worldwide, and its forms are more and more diverse [1]. There are many institutions in the coalition system, and they can be defined as the Agents. For the development of the coalition, the agents would submit information obtained to the coalition to analyze and process. However, the information from each agent may be complementary or conflicting. Thus the information should be fused reasonably. Redundant or useless information should be removed, and comprehensive and complete information should be obtained through analysis [2-3]. Development strategy of the coalition could have a scientific and reliable basis based on information fusion [4-5]. Therefore, there are important theoretical and practical significance to study information fusion of agent coalitions.
The rough set theory provides a natural theoretical models and formal methods for information fusion. In 1982 Pawlak[6], a Polish scholars, proposed rough set theory . He argued that things tended to have a variety of attributes, but each attribute was not equally important. Some of the attributes might be redundant, and these attributes should be reduced. Its core idea is attribute reduction that is to remove the irrelevant or unimportant attributes and maintain the capabilities of knowledge classification [7-8]. Rough set theory is widely applied in the fields of physiotherapy diagnosis, fault diagnosis, pattern recognition and image processing. Tsumoto[9] used rough set theory to extract diagnosis rules from the medical database and developed a medical diagnostic model . Zhong[10] discussed the knowledge discovery process through rough set theory . Greco[11] combined rough set theory and consumer preferences in economics, and analyzed the consumer satisfaction . While the application of rough set theory was investigated in various fields, the methods for data preprocessing, attribute reduction algorithm and the value reduction algorithm were improved and explored in order to analyze the data more conveniently and efficiently [12-13].
The evaluation model of capability of multiple agent coalitions based on information fusion would be developed in this study. Indicators were reduced by attribute reduction method based on rough set theory. New indicator system was established and weights of indicators were calculated by entropy weighting method. Nearest neighbor method was utilized to evaluate the capability of multiple agent coalitions. The results of information fusion model were obtained and compared with the results of cloud evaluation model and D-S evidence method. This method would get comprehensive and integrated evaluation results, and provided scientific, rational decision support for the system to choose the best agent coalition.
2 Theory and Method 2.1 Attribute Reduction Based on Rough Set TheoryAccording to the rough set theory, the information system is expressed as S=(U, C, V, f), where U={x1, x2, …, xm} is the discourse domain, which is a non-empty finite set of objects;C={s1, s2, …, sn} is a non-empty finite set of attributes; V=∪Vs is the range of the attribute s; f : U×C→Vs information function, ∀(x, s)∀U×C, f (x, s)∀Vs [14]. In the information system established in this study, condition attributes would only be considered, and the decision attribute would not be included.
Definition 1 For one non-empty set B⊆C, indiscernible relation IB of B on U can be defined as:
| ${{I}_{B}}=\left\{ \left( x, y \right)\in U\times U:f\left( x, s \right)=f\left( y, s \right), \forall s\in B \right\}$ | (1) |
Definition 2 while X is one non-empty set of U, for an equivalence relation B∈ind(S), the lower and upper approximation of the set X, can be defined as:
| $\begin{align} & {{I}_{B}}=\left\{ \left( x, y \right)\in U\times U:f\left( x, s \right)=f\left( y, s \right), \forall s\in B \right\} \\ & \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{B}\left( X \right)=\left\{ x\in U:{{I}_{B}}\left( X \right)\subseteq X \right\} \\ \end{align}$ | (2) |
| $\bar{B}\left( X \right)=\left\{ x\in U:{{I}_{B}}\left( X \right)\cap X\ne \varnothing \right\}$ | (3) |
Definition 3 For two attribute sets A, D⊆C, x∈U/D,
Definition 4 Approximate classification quality γ (A, D) can be defined as:
| $\gamma \left( A, D \right)=\frac{\underset{X\in U/D}{\mathop{\sum }}\, \left| \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A}\left( X \right) \right|}{U}$ | (4) |
γ(A, D) is also called the dependence between A and D. It stands by the object that can be classified accurately accounted for the proportion of the entire system.
According to all definitions above, the degree of importance of each attribute indicator can be determined. The degree of importance of each attribute can be measured based on the impact on the classification ability, while one attribute sj is removed from the attribute set C [15]. This basic idea is that each attribute indicator would be removed from the attribute set successively, and changes in classification would be investigated without this indicator. If one attribute indicator is removed, and great changes occur to the classification correspondingly, this indicates that the attribute indicator has high degree of importance. Otherwise, the importance of this attribute indicator is low. Thus the importance of one attribute sj can be defined as:
| $sig\left( {{s}_{j}} \right)=\frac{\left| po{{s}_{R}}\left( R \right) \right|-\left| po{{s}_{(R-\{{{s}_{j}}\})}}\left( R \right) \right|}{\left| po{{s}_{R}}\left( R \right) \right|}$ | (5) |
Where sj∈R, R∈A, | E | denotes the number of elements in the set.
If sig(sj)=0, the importance of the attribute sj is low, and it can be reduced from the attribute set. In this study information from multisource with different attributes would be reduced according to rough set theory. Redundant information would be removed. Information of different indicators would be fused based on fusion algorithm, and comprehensive description of the object would be obtained.
2.2 Entropy Weighting MethodIn the evaluation system, designing weights of the indicators is an important process. It can measure the impact of indicators on the capability of the agent coalition. When the weight of an indicator is high, it has great impact on the capability; otherwise, the impact is inferior.
In information theory, information entropy is an important concept, and it can measure the degree of disorder in the system, as well as the amount of useful information that the data provide [16]. When an indicator of the evaluated objects is of great differences, its entropy must be low. This shows that this indicator can contribute more useful information. Thus its weight should be correspondingly set high. Otherwise, its weight should be low [17]. In this study entropy weighting method is used to weight the indicators of the capability of the agent coalition, and the procedures are as follows.
1) The original data of all indicators should be normalized, and this can eliminate the impact of dimension. For one benefit indicator, the equation is
| ${{r}_{ij}}=\frac{{{x}_{ij}}-\underset{i}{\mathop{min}}\, \left\{ {{x}_{ij}} \right\}}{\underset{i}{\mathop{max}}\, \left\{ {{x}_{ij}} \right\}-\underset{i}{\mathop{min}}\, \left\{ {{x}_{ij}} \right\}}\text{ }$ | (6) |
And for a cost indicator, it is
| ${{r}_{ij}}=\frac{\underset{i}{\mathop{max}}\, \left\{ {{x}_{ij}} \right\}-{{x}_{ij}}}{\underset{i}{\mathop{max}}\, \left\{ {{x}_{ij}} \right\}-\underset{i}{\mathop{min}}\, \left\{ {{x}_{ij}} \right\}}$ | (7) |
Where, xij(i=1, 2, …, m, and j=1, 2, …, n) is the monitoring value of the j-th object on the i-th indicator, and rij is the dimensionless value normalized.
2) For the evaluation problem with m indicators and n objects evaluated, the entropy value pi of the i-th indicator can be defined as:
| ${{p}_{i}}=-k\sum\limits_{j=1}^{n}{{{f}_{ij}}}ln{{f}_{ij}}$ | (8) |
Where
3) The weight of the i-th indicator λi can be calculated according to the entropy theory:
| ${{\lambda }_{i}}=\left( 1-{{p}_{i}} \right)/\left( m-\sum\limits_{i=1}^{m}{{{p}_{i}}} \right)\text{ }$ | (9) |
Where 0≤λi≤1, and
The nearest neighbor method would be specifically introduced in this section. Its basic ideas are as follows[18]. For an evaluation problem with multiple objects, it is supposed that there are multiple samples xi (i=1, 2, … , N). For one sample xi to be classified, we investigate the distances between xi and x* whose classification is already known. The cluster of sample xi is defined as the cluster with the nearest distance from the known cluster. According to this classification ideology, the function of the distance of nearest neighbor method is:
| ${{d}_{i}}=\underset{i}{\mathop{min}}\, \left\| {{x}_{i}}-{{x}^{*}} \right\|$ | (10) |
The Euclidean distance function is employed in this study, and the equation is:
| ${{d}_{i}}\left( {{x}_{i}}-{{x}^{*}} \right)=\sqrt{\underset{i}{\mathop{\sum }}\, {{\left( {{x}_{i}}-{{x}^{*}} \right)}^{2}}}$ | (11) |
In our evaluation system, the data of indicators should be normalized first in order to eliminate the impact of dimensions. After that we consider the distance from the evaluation object xi to the optimal solution x*, and the closeness degree Ti can be defined as:
| ${{T}_{i}}=1-{{d}_{i}}\left( {{x}_{i}}, {{x}^{*}} \right)$ | (12) |
Obviously 0≤ Ti ≤1. The closer xi is to the optimal solution, the closer Ti is to 1. Otherwise, the farther xi is to the optimal solution, the closer Ti is to 0. Thus Ti can be ordered, and satisfactory evaluation results can be obtained.
The nearest neighbor method is a practical evaluation method. It is suitable for processing the problems of multi-attribute decision making. While this method is applied to the evaluation work, good comparability assessment results can be obtained. It has simple principle, easy calculation and high practicability.
3 Evaluation Model of Agent Coalition Capability 3.1 Information Fusion of Agent CoalitionThe enterprise agent coalition is an alliance which consists of enterprises, research institutes, universities and other institutions, and these institutions can be defined as the agent. They tend to have a common goal or some common features [19-20]. While the information is transferred and applied between the agents of the coalition, the process tends to be synergetic and complicated. Thus the perception, classification and integration of the information usually need lots of work. This brings trouble to the decision-making. Technology of information fusion is an important tool in knowledge management field. Information from different knowledge sources can be effectively organized, and formed a new and more comprehensive knowledge [21-22]. Information fusion in enterprise agent coalition is the process that the information from coalition members and external sources would be collected, transferred, fused and applied between agents of the coalition. Thus the process of sharing, delivery and integration of knowledge can be well promoted.
The process of information fusion in enterprise agent coalition is shown in Fig. 1, and its procedure is as follows. 1) Information would be acquired from all agents including suppliers, customers, competitors, enterprises, governments, universities and other institutions. 2) The information obtained from multiple sources should be classified and sorted according to its features, and the excess and useless information should be removed. In this step different types of information are ruled as independent from each other. 3) All types of information would be fused, and the final decision can be obtained according to the new knowledge. A reasonable and effective algorithm is the key of this step. Appropriate adjustment is necessary in accordance with the actual conditions, as well as dynamics and complexity of development process itself.
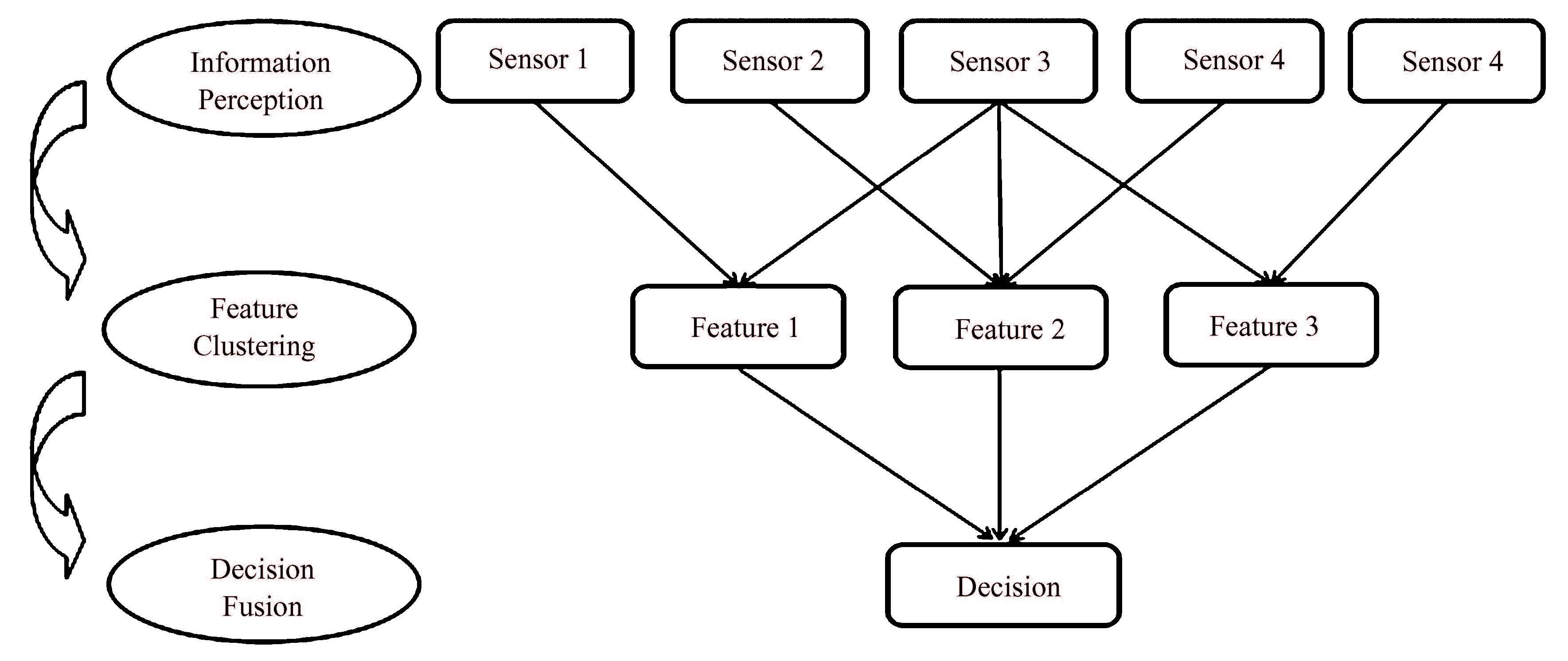
|
Figure 1 Architecture of information fusion |
Fusion algorithm is an important core of information fusion, and it is a method that can fuse multi-source information into the comprehensive knowledge [23-24]. Because of the diversity and complexity of information itself, and different capacity of information processing for different coalition, information fusion algorithms applied in different fields are also often different [25-26]. Information are obtained from multicourse, and analyzed and processed by the agent coalition. Information with different attributes would be reduced according to rough set theory in this study. Redundant information would be removed. New indicator system would be formatted. Capability of multiple agent coalitions would be evaluated and comprehensive and integrated decision-making information would be obtained.
3.2 Algorithm of Evaluation ModelThe information fusion model was applied in the evaluation of capability of multiple agent coalitions in this study. The original indicators were reduced by the attribute reduction method based on rough set theory. Entropy weighting method was used to determine the weights of the remaining indicators. Nearest neighbor method was utilized to evaluate the capability of multiple agent coalitions. Thus comprehensive and integrated evaluation results were hoped to be obtained, and they could provide a scientific basis for the decision-making of development strategies for agent coalitions. The information fusion algorithm of the research problems is shown in Fig. 2.

|
Figure 2 Algorithm of evaluation model |
According to Fig. 2, the procedures of evaluation method of capability of agent coalitions based on information fusion are designed as follows.
Step 1: Initialize, and get the original data of all indicators of agent coalition capability;
Step 2: Select the indicators and reduce the attribute based on rough set theory. Thus the redundant indicators were removed and the evaluation workload could be reduced;
Step 3: Use entropy weighting method to determine the weights of remaining indicators and analyze the importance of indicators;
Step 4: Use nearest neighbor method to evaluate capability of agent coalitions;
Step 5: Analyze and discuss evaluation results compared them with other methods;
Step 6: Draw conclusions, and provide reasonable suggests for decision making.
4 Simulation Experiment and Results Analysis 4.1 Simulation ExperimentThe indicators and data of capability of agent coalitions were from Ref. [27] in this experiment. The decision to make was to choose the best coalition from a number of the agent coalitions. Capacity needs of this task t were set 200. The alternative coalition set was {C1, C2, …, C10}, and evaluation indicator set was {s1, s2, s3, s4}, which represented "task consumption", "communication overhead", "ripe degree" and "sustainability" respectively, where "sustainability" stood by the capacity that the coalition could undertake follow-up mission under the condition of current task demand. Evaluation domains of all indicators are shown in Table 1. For task t, specific values of evaluation indicators of ten agent coalitions are shown in Table 2. The indicators of s1 and s3 were benefit indicators, that is, the bigger the better; the indicators of s2 and s4 were cost indicators, that is, the smaller the better. The evaluation value should be higher, while the task consumption of one agent coalition was closer to the capacity needs of task t, its communication overhead was lower, its ripe degree was larger, and its sustainability was better.
| Table 1 Evaluation domain of indicators |
Attribute reduction based on rough set theory would be carried out based on the data in Table 2 in this step. However, the data in rough set have to be discrete, so the original data should be discretized.The processes are as follows.
| Table 2 Specific values of evaluation indicators |
1) Normalize original data of all indicators to eliminate the impact of dimension;
2) The strength of the capability of agent coalitions should be fuzzified. Capacity is divided into three levels, that is, the Evaluation Space is ES={“Weak”, “Moderate”, “Excellent”}. They are quantized into discrete values of levels. The quantitative criteria of capabilities of agent coalitions are shown in Table 3.
| Table 3 Quantitative criteria of capabilities of agent coalitions |
The capacity was divided into five levels in Ref. [27], that is, the Evaluation Space was ES={“Very weak”, “Weak”, “Moderate”, “Good”, “Excellent”}, while there were just three levels. The division of five levels helped a lot to distinguish the evaluation results. It made the capability of agent coalitions be divided more detailed. But it may increase more workload to a certain extent inevitably. The division of three levels was simpler, and it was enough to distinguish the capability. At the same time it reduced the workload, and this made the process efficiently.
3) Calculate the membership of each indicator based on fuzzy logic.At last the individual levels of each indicator were defined as the discrete values, and the results are shown in Table 4.
| Table 4 Discrete results of original data |
According to the data in Table 4, the processes of attribute reduction based on rough set theory are shown as follows.
(1) The discourse domain is U={C1, C2, C3, C4, C5, C6, C7, C8, C9, C10}The condition attribute set is C={s1, s2, s3, s4};
(2) Investigate the classification of U on each set:
U/C={C1, C2, C3, C4, C5, C6, C7, C8, C9, C10}
U/{C-{s1}}={C1, {C2, C4}, {C3, C10}, C5, C6, C7, C8, C9}
U/{C-{s2}}={C1, C2, C3, C4, C5, C6, C7, C8, C9, C10}
U/{C-{s3}}={C1, {C2, C10}, C3, C4, {C5, C9}, C6, C7, C8}
U/{C-{s4}}={C1, {C2, C6}, C3, C4, C5, C7, C8, C9, C10}
(3) Calculate the positive domain:
pos{C-{s1}}(C)={C1, C5, C6, C7, C8, C9}
pos{C-{s2}}(C)={C1, C2, C3, C4, C5, C6, C7, C8, C9, C10}
pos{C-{s3}}(C)={C1, C3, C4, C6, C7, C8}
pos{C-{s4}}(C)={C1, C3, C4, C5, C7, C8, C9, C10}
(4) Calculate the importance of the attribute:
| $sig\left( {{s}_{1}} \right)=\frac{\left| po{{s}_{C}}\left( C \right) \right|-\left| po{{s}_{(C-\{{{s}_{1}}\})}}\left( C \right) \right|}{\left| po{{s}_{C}}\left( C \right) \right|}=0.4$ |
| $sig\left( {{s}_{2}} \right)=\frac{\left| po{{s}_{C}}\left( C \right) \right|-\left| po{{s}_{(C-\{{{s}_{2}}\})}}\left( C \right) \right|}{\left| po{{s}_{C}}\left( C \right) \right|}=0$ |
| $sig\left( {{s}_{3}} \right)=\frac{\left| po{{s}_{C}}\left( C \right) \right|-\left| po{{s}_{(C-\{{{s}_{3}}\})}}\left( C \right) \right|}{\left| po{{s}_{C}}\left( C \right) \right|}=0.4$ |
| $sig\left( {{s}_{4}} \right)=\frac{\left| po{{s}_{C}}\left( C \right) \right|-\left| po{{s}_{(C-\{{{s}_{4}}\})}}\left( C \right) \right|}{\left| po{{s}_{C}}\left( C \right) \right|}=0.2$ |
The importance of attribute indicator s2 was 0, and indicator s2 was reduced from the original indicator set based on rough set theory. The remaining indicators were s1, s3 and s4, and they could reestablish new indicator system. Indicator s2 was reduced, and this illustrated that its functions to reflect the agent coalition could be ignored. Indicator s2 might have great relevance with other indicators. Indicator s2 denoted communication overhead. The communication overhead of one Agent coalition usually had to be large, while the coalition needed to consume much resource to accomplish the task. Meanwhile its ripe degree and sustainability were not great.
While indicator s2 was reduced, the elements of the evaluation indicator set were reduced from 4 to 3. Thus the number of original data decreased, and this reduced the workload of evaluation. While there were more than ten or more indicators, the workload of evaluation might be huge. At this time the attribute reduction had to be essential. Information from too many indicators might usually have correlation more or less. If the information with correlation were used to research, the complexity and workload would increase, and meanwhile the results were not reasonable yet. Therefore, before the evaluation study, it would be better to use attribute reduction based on rough set theory to analyze the importance of indicators and reduce the redundant information. It was of great significance in theoretical and practical.
4.2 Analysis and DiscussionAfter the indicators were reduced, new indicator set was formatted. The entropy values and weights of indicators in the new indicator set according to entropy weighting method are shown in Table 5.
| Table 5 Entropy values and weights |
From Table 5, we could see that the weight of indicator s4 was the largest, while that of s2 was the smallest. However, the difference between three indicators was little, and this illustrated that the remaining indicators were all important to the evaluation system.
The capabilities of ten agent coalitions were evaluated by nearest neighbor method, and the results are shown in Table 6.
| Table 6 Evaluation results of nearest neighbor method |
From Table 6, we could see that C10 was the best coalition among all agent coalitions, while C7 was the worst. For task t, C10 had low consumption and communication overhead, and its ripe degree and sustainability were the best. The consumption and communication overhead of C7 were both large, its ripe degree was the worst, and the sustainability was worse. These caused C7 be the worst coalition.
The results in this study were compared with that of “cloud evaluation model” in Ref. [27] and “D-S evidence method” in Ref. [28]. They are shown in Table 7, and coalition rankings from excellent to weak are shown in Table 8.
| Table 7 Evaluation values of three different methods |
| Table 8 Rank of all agent coalition of three different methods |
As we could see in Table 8, the results obtained by three methods had little difference. C10 and C2 were the best two coalitions, and the results of three methods were the same.C1, C3, C4, C5 and C6 were in the midstream, the results of three methods had small differences. This was because that the five coalitions in midstream all had their own advantages and disadvantages, and there was no absolutely stronger than the others. However, three methods had some consistent results: C5 was better than C4, and C1 reached the last in the midstream. This was consistent with the actual situation according to the data in Table 2.C7, C8 and C9 were in the downstream, and C7 was the worst coalition in all three methods. To sum up, the reasonable results were still obtained under the situation that some attribute indicator was reduced. This illustrated that this method was feasible.
On the other hand, from Table 7, the results of D-S evidence method did not have obvious discrimination. The evaluation values were very close to each other. In particular, the values of C3, C4, C5 and C6 differed only about 0.001. It might not be reasonable to evaluate the capability of multiple agent coalitions according to these tiny differences. However, discrimination of evaluation values of information fusion method in this study and cloud evaluation model were obvious, and they conducive to decision-makers to make judgments. In summary, the reasonable results were obtained based on information fusion method in this study, and the workload was reduced. This study provided scientific, rational decision support for the system to choose the best agent coalition, and provided innovative steps for the evaluation of capability of agent coalitions.
5 ConclusionsThe evaluation model of capability of multiple agent coalitions based on information fusion was employed. Indicators of capabilities were reduced according to the importance of indicators based on rough set theory. This process reduced the evaluation workload. When the indicators were too many or had strong correlation, attribute reduction could removed the redundant information, and reestablish the indicator system. Entropy weighting method was used to determine the weights of the remaining indicators. Nearest neighbor method was utilized to evaluate the capability of multiple agent coalitions. Thus comprehensive and integrated evaluation results were obtained. Compared with the results of cloud evaluation model and D-S evidence method, the results of information fusion model were reasonable and with good discrimination. The information fusion model provided a rational basis for decision making of the agent coalitions.
| [1] |
Lin C H, Wu Y J, Chang C C, et al. The alliance innovation performance of R&D alliances—The absorptive capacity perspective.
Technovation,2012, 32 (5) : 282-292.
( 0) 0)
|
| [2] |
Lee H, Lee B, Park K, et al. Fusion techniques for reliable information: a survey.
International Journal of Digital Content Technology and its Applications,2010, 4 (2) : 74-88.
( 0) 0)
|
| [3] |
Solaiman B, Bossé É, Pigeon L, et al. A conceptual definition of a holonic processing framework to support the design of information fusion systems.
Information Fusion,2015, 21 : 85-99.
( 0) 0)
|
| [4] |
Pavlin G, Patrick D O, Michiel K, et al. Dynamic process integration framework: A novel approach to efficient implementation of robust distributed information fusion systems. Proceedings of Fusion 2011-14th International Conference on Information Fusion. Chicago, 2011. 5-8.
( 0) 0)
|
| [5] |
Deng X Y, Deng Y. Multisensor information fusion based on dempster-shafer theory and power average operator.
Journal of Computational Information Systems,2013, 9 (16) : 6417-6424.
( 0) 0)
|
| [6] |
Pawlak Z. Rough set.
International Journal of Information and Computer Science,1982, 11 (5) : 341-356.
( 0) 0)
|
| [7] |
Dubois D, Prade H. Rough fuzzy sets and fuzzy rough sets.
International Journal of General Systems,1990, 17 (2/3) : 191-209.
( 0) 0)
|
| [8] |
Do ng, L X, Xiao D M, Liu Y L. Rough set and radial basis function neural network based insulation data mining fault diagnosis for power transformer.
Journal of Harbin Institute of Technology (New Series),2007, 14 (2) : 263-268.
( 0) 0)
|
| [9] |
Tsumoto S. Mining diagnostic rules from clinical databases using rough sets and medical diagnostic model.
Information Science,2004, 162 (2) : 65-80.
( 0) 0)
|
| [10] |
Zhong N, Skowron A. A rough set-based knowledge discovery process.
International Journal of Mathematics and Computer Science,2001, 11 (3) : 604-615.
( 0) 0)
|
| [11] |
Greco S, Matarazzo B, Slowinski R. Customer satisfaction analysis based on rough set approach.
Journal of Business Economics,2007, 77 (3) : 325-339.
( 0) 0)
|
| [12] |
Yang X B, Yang J Y, Hu X H. A new rough set model for knowledge acquisition in incomplete information system. Proceedings of 2009 IEEE International Conference on Granular Computing. Nanchang, 2009. 17-19.
( 0) 0)
|
| [13] |
Li H X, Zhou X Z. Risk decision making based on decision-theoretic rough set:A three-way view decision model.
International Journal of Computational Intelligence Systems,2011, 4 (1) : 1-11.
( 0) 0)
|
| [14] |
Nguyen H S, Pal S K, Skowron A. Rough sets and fuzzy sets in natural computing.
Theoretical Computer Science,2011, 412 (42) : 5816-5819.
( 0) 0)
|
| [15] |
Miao D Q, Li D G.
Theory, Algorithms and Applications of Rough Set. Beijing: Tsinghua University Press, 2008 : 156 -173.
( 0) 0)
|
| [16] |
Liu L, Zhou J Z, An X L, et al. Using fuzzy theory and information entropy for water quality assessment in three gorges region, China.
Expert Systems with Applications,2010, 37 (3) : 2517-2521.
( 0) 0)
|
| [17] |
Qu X J, Chen H, Peng G H. Novel detection method for infrared small targets using weighted information entropy.
Journal of Systems Engineering and Electronics,2012, 23 (6) : 838-842.
( 0) 0)
|
| [18] |
Kazuo H, Yasunobu T. Effective algorithms for the nearest neighbor method in the clustering problem.
Pattern Recognition,1993, 26 (5) : 741-746.
( 0) 0)
|
| [19] |
Yang X P, Yao J T. Modelling multi-agent three-way decisions with decision-theoretic rough sets.
Fundamenta Informaticae,2012, 115 : 157-171.
( 0) 0)
|
| [20] |
Xu B, Peng Z P, Yu J P, et al. Multi-tasking agent coalition formation based on quantum multi-objective evolutionary algorithm.
System Engineering Theory and Practice,2012, 32 (10) : 2253-2261.
( 0) 0)
|
| [21] |
Wu Z F, Huang H K, Zhao X. Binary-encoding differential evolution algorithm for agent coalition.
Computer Research and Development,2008, 45 (5) : 848-852.
( 0) 0)
|
| [22] |
Shehory O, Gal K, Eran S.Multi-agent coalition re-formation and league ranking. Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems.New York, 2004. 19-23.
( 0) 0)
|
| [23] |
Sannen D, Hendrik V B. A multilevel information fusion approach for visual quality inspection.
Information Fusion,2012, 13 (1) : 48-59.
( 0) 0)
|
| [24] |
Ribeiro R A, António F, André M, et al. A fuzzy information fusion algorithm based on multi-criteria decision making.
Knowledge-Based Systems,2014, 58 : 23-32.
( 0) 0)
|
| [25] |
Wang H, Peng J, Wu W. Fusion algorithm for multisensor images based on discrete multiwavelet transform.
Vision, Image and Signal Processing,2002, 149 (5) : 283-289.
( 0) 0)
|
| [26] |
Zlatko Z, Galina V, Zoheir S. Agile data fusion and knowledge base architecture for critical decision support.
International Journal of Decision Support System Technology,2013, 5 (2) : 1-20.
( 0) 0)
|
| [27] |
Tian J B, Jiang J G, Zhang G F, et al. Evaluation of agent coalition based on cloud model.
Control and Decision,2013, 28 (1) : 152-156.
( 0) 0)
|
| [28] |
Su Z P, Jiang J G, Xia N, et al. An evaluation method for agent coalition based on d-s evidence theory.
Pattern Recognition and Artificial Intelligence,2007, 20 (5) : 624-629.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


