Owing to the need for higher passive safety and reduction of weight, in automotive production, the use of ultra high strength steel components has increased. Unfortunately, the forming of ultra high strength steel sheet has some disadvantages like unacceptably high stresses and significant spring-back phenomena, thus making traditional cold sheet metal forming technologies unsuitable.
In recent years, a novel technology named hot stamping has beenconsidered as a solution to overcome the above-mentioned difficulties[1-2]. Less springback and the high forming precision of hot stamping has attracted the attention of the automotive industry, and much research in this field is being carried out.Mori et al.[3] proposed a new hot stamping process of ultra high tensile strength steel sheets, which directly heated the sheets set into the dies by means of the electrical resistance. Manuelet al.[4]developed a series of thermo-mechanical tailored processing of sheets, based on the adequate application of differential heating and cooling strategies.
However, the susceptibility to temperature and stress of complex geometries products during thermo-mechanical process operation may cause the cracking of stamping steel[5-6]. Moreover, the influences of the hot stamping process condition on the product’s performance are nonlinear, time-variable and indeterminate. Therefore, the conventional dies-test method, depending on the case and experience, hardly meets the requirements of manufacturers. The numerical simulation of sheet metal forming processes has proven its efficiency and usefulness, considering its short research cycle and affordable cost. Presently, many researchers have focused on the combination of FE simulations and optimization technology to solve the process problem of sheet metal hot forming. For example, Satoshi et al.[7] developed a technique with the control of punch speed and blank holder force (BHF) via sequential approximate optimization (SAO). Hoffmann et al.[8] implemented a new method based on systematic optimization to design cooling ducts in tool of hot stamping. Ingarao et al.[9]integrated numerical simulations, the response surface methodology (RSM) and Pareto optimal solutions search techniques to optimize friction conditions and blank holder.
As is well known, complex optimization problems usually contain a great numbers of local optima. Solutions obtained from optimization methods are easily trapped into a local optimum region. Currently, the approach to address this problem is to generate sample points using pseudo-probabilistic technique such as Latin hypercube sampling [10] or low discrepancy sequence sampling such as Hammersley sequence sampling (HSS) [11]. Preechakul[12] has already reported that the low discrepancy sequence sampling is less random than a pseudo-random number sequence, but it tends to sample search space more uniformly than random numbers.This paper proposes using HSS based on low discrepancy sequence sampling strategies for the design of experiment (DOE).
In this work, a hybrid optimization strategy based on Hammersley Sequence Sampling (HSS), finite analysis, back-propagation (BP) neural network and genetic algorithm (GA) is posed. This strategy is applied to identify the process parameters of hot stamping. A model of auto reinforcement is used as an application example to verify the feasibility of the optimized strategy. The finite-element model is established and will be used in subsequent research.
2 Problem Description 2.1 FE ModelingThe considered forming process is a realistic hot stamping one aimed to obtain auto reinforcement (see Fig. 1 for a sketch of the investigated process).The tool system mainly includes die, punch, cooling loops and blank holder. The material used in this study is BR1500HS steel.In the hot stamping process, the first step is to heat the blank from room temperature to the austenization temperature. The next step is to transfer the hot blank from the heating oven to the tools. The blank loses heat by convection and radiation heat transfer to the environment. Different forming temperatures ranging from around 700 ℃ to 900 ℃ can be obtained by air cooling the heated blank before blank is placed on the die.After forming, the blank is cooled by means of tool with integrated cooling holes, which results in the transformation of austenite into martensite. By means of hot stamping, high strengths up to 1 500 MPa and high dimensional stability after the forming process can be attained.

|
Figure 1 Hot forming tool system for the auto reinforcement part |
Coupled thermo-mechanical analysis is used to predict the material behavior during the hot stamping process. In this section, there are some issues to be taken into account:
⑴ An inverse installing tool has been adopted in the real stamping process. The tools are treated as rigid objects without any elastic deformation.
⑵ The fully integrated shell element with five gauss thickness dimensional integrating points is used to mesh the blank, whose thickness is 1.8 mm. In detail, the initially number of blank elements is 9 600. The refinement level of the mesh is set to 2.
⑶ The temperature of tools are set to 50 ℃ and remain unchanged.The die velocity is 100 mm/s, according to the actual stamping process.It is assumed that the blank has an initial homogeneous temperature.The equivalent interfacial heat transfer coefficient between the blank and tools of 4 500 W/m2·℃ is obtained from Hoffmann[13].
2.2 Material Law and PropertiesThe reliability of the numerical simulations depends not only on the models and methods used, but also on the accuracy and applicability of the input material data. The utilized material was ultrahigh strength steel(BR1500HS, 1.8 mm) for which the following flow rules were obtained through uniaxial tensile tests at elevated temperatures. Generally speaking, the stress-strain curves (flow stress) of the sheet material at elevated temperatures should be temperature and strain rate dependent[14].The shape of the specimen is illustrated in Fig. 2. Experiment was tested on the thermal simulation machine Gleeble-1500D. Because the utilized steel material mechanical properties are insensitive to the direction of rolling, the test does not involve that.
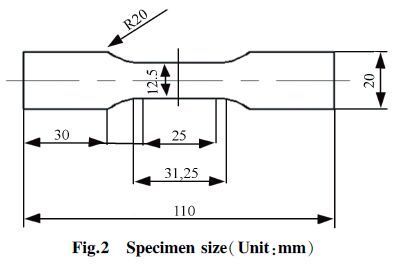
|
Figure 2 Specimen size(Unit:mm) |
There are Material model 106 (MAT-106 in LS-DYNA) which is an elastic visco-plastic material model with thermal effects. Material properties used for BR1500HS steel are presented in the following figures and tables.The symbols in Fig. 3 show the Gleeble tensile test results for BR1500HS steel at different strain rates (0.01, 0.1 and 1 s-1) and different deformation temperatures (600, 700, 800 and 900 ℃). The increase of temperature leads to a significant reduction of the flow stress and decrease of work hardening exponent, resulting in a noticeable decrease of the slope of the true stress-strain curves. Besides the temperature, the strain rate influences the flow properties of BR1500HS steel.The flow stress increases with the increase of strain rate, which has thus to be considered in characterizing the material properties.
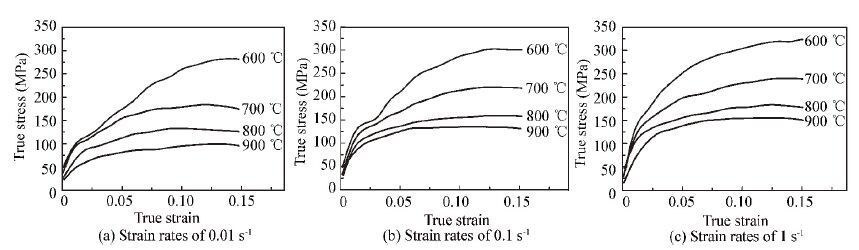
|
Figure 3 True stress-strain curves for BR1500HS steel corresponding to different deformation temperatures and strain rates |
Viscous effects are accounted for using the Cowper and Symonds model, which scales the yield stress with the factor:1+(ε·ρ/c)1ρ, c and ρ have strong temperature dependence but are weak functions of strain rate. Also required are thermal conductivity and coefficient of thermal expansion, each as a function of temperature.This type of variational relationship was considered in the finite element software(see Table 1).
| Table 1 Thermal-mechanical material properties for BR1500HS boron steel |
2.3 Simulation Results
The numerical simulations are carried out.The process parameters of the finite element model are defined as follows:the initial stamping temperature of the sheet is 750 °C;the blank hold force is 200 kN and the friction coefficient is 0.125.The thickness reduction ratio is one of the most important values in stamping processes, because it is directly related with the appearance of cracks and, therefore, the failure of the part (the circle in Fig. 4).Usually a thickness reduction of 20% is allowed in automotive part design.Verification is conducted and the results indicate that for these portions, the simulative and test values are in good agreement.Failures (cracking) are observed in the hot stamping of BH1500HS tests, emanating from the round corner area.
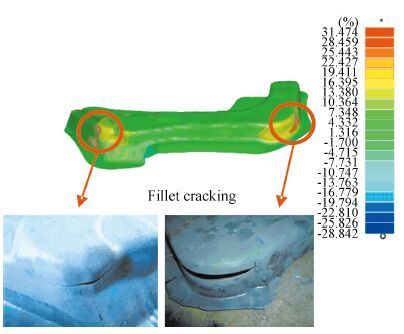
|
Figure 4 Thinning distribution for one of the analyzed cases |
More specifically, the following conclusions can be drawn from the experimental results.
Because the round corner area of work-piece in contact with die early, the time elapsed from when die and sheet first come into contact until the end of forming is higher than other area.This results in a higher temperature reduction in the region of contact, in turn, the metal of round corner area becomes stronger than other area not in contact with the die (see Fig. 4 which shows hotter high strength steel has a relatively higher ductility and lower flow stress).As is well known, the type of high strength steel sheet, which greater strength is at the expense of formability, makes the metal less easier to inflows.Hence, the eventual failure is initiated by cracking resulting from excessive strain in the round corner location.
It is necessary to explore the feasible forming process parameters and seek the optimal process parameter sets, because of the possibility of fracture exists.
3 Optimization Strategy 3.1 Design VariablesIn the investigated processes two design variables are chosen, namely initial forming temperature and blank holder force value (BHF). Actually, the considered process factors are defined as the design variables of the optimization in this section strongly influence the formability and quality of the sheet metal parts. In the manufacturing factory, the friction that affects the quality of the product is not analyzed quantitatively but is instead determined by lubrication, tool materials and coating. Given this, the friction coefficient is considered a fixed value (0.125) in this work.
3.2 Forming Quality IndicatorIn the manufacturing factory, a range of acceptable thinning levels is requested. If the max-thinning rate is above a certain threshold, the sheet metal cracks.Thus, in order to prevent fracture occurrence, the thinning distribution is pursued. At the end of each numerical simulation this variable is collected and considered as a fracture risk indicator. For instance, the corresponding max-thinning rate is 31.47 %, and the allowable thinning in industry is usually set to 20 %. As a result, the work-piece has a tendency to crack (See Fig. 6 reporting a typical obtained thinning distribution).
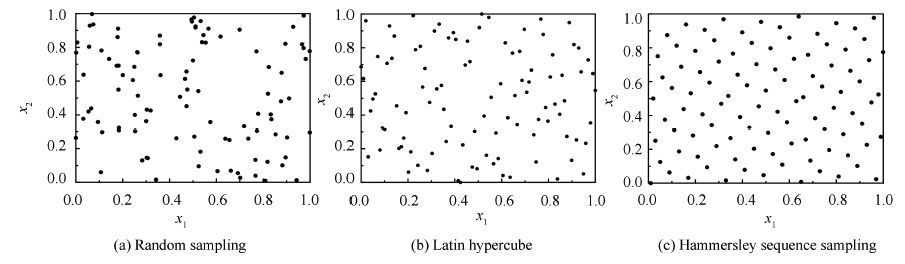
|
Figure 5 100 points in the unit squares generated by random sampling, LHS and HSS |
|
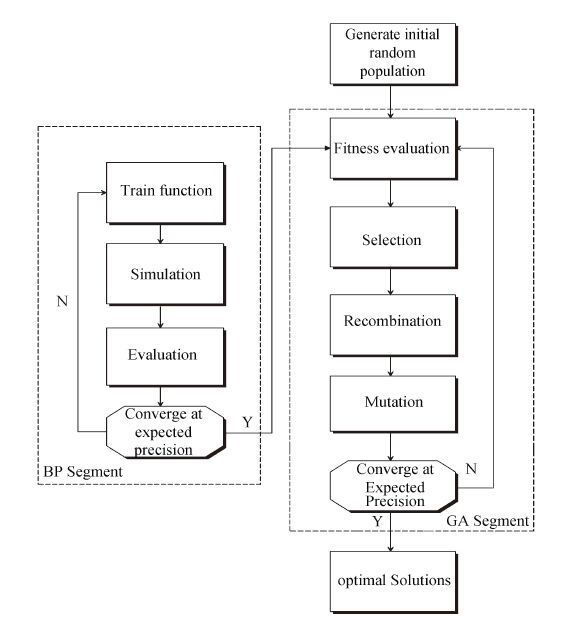
Figure 6 Flow chart of combining BP neural network and genetic algorithm |
The maximum thinning is chosen instead of forming limit diagram(FLD) .Such choice is justified if an industrial environment is taken into account, because that FLD do not perform well if non-linear strain paths are concerned[15]. Moreover, the FLD can be considered a qualitative tool rather than a quantitive tool to predict fracture in particular if complex stamping operations are taken into account. On the other hand, the utilization of forming limit stress diagrams is considered a good tool to represent fracture limits but such diagrams need to be properly tuned to derive a proper indicator of fracture risk. Such considerations, together with the observation that in an industrial environment a quick and simple fracture indicator is necessary led to the choice of maximum thinning as objective function.
According to the hot stamping process, the upper and lower initial forming temperature boundaries are 700 ℃ and 900 ℃, respectively. The blank hold force range is 100-300 kN, based on the aforementioned BHF of 200 kN.In industry applications, a stamped AHSS part with maximum thickening rate exceeding 5% is usually considered to have a large risk of wrinkling. According to the considerations mention above, the objective function is:
| $\left\{ \matrix{ {\rm{min}}{t_{{\rm{max}}}}\left( x \right), t\left( x \right) \ge 0 \hfill \cr {T_{{\rm{max}}}}\left( x \right) \le {T_0} \times 105\% \hfill \cr t\left( x \right) = \left[ {\left( {{T_0} - {T_{{\rm{min}}}}\left( x \right)} \right)/{T_0}} \right] \times 100\% \hfill \cr x = \left[ {{x_1}, {x_2}} \right], {x_1} \in \left[ {700, {\rm{ }}900} \right], {x_2} \in \left[ {100, {\rm{ }}300} \right] \hfill \cr} \right.$ |
where T0 is the initial sheet thickness;Tmax(x) and Tmin(x) denote the maximum sheet thickness and the minimum sheet thickness, respectively, and x1, x2 are the design variables. The maximum thinning rate is denoted by tmax(x).
3.3 Optimization StrategyOnce the optimization problem is modeled, the workflow procedure applied in the present paper is developed according to the following steps:
Step 1 Planning of the numerical simulations to be run through a proper Design of Experiments (DOE) definition using HSS sampling technique.
Step 2 Collection of numerical data obtained on thickness minimum for each of the conditions identified by the DOE.
Step 3 BP-GA step: A BP neural network model is developed to obtain the mathematical relationship between optimization goal and design variables, and genetic algorithm is used to optimize the process parameters.
Next, the steps of the above illustrated procedure with particular reference will be describe in detail to the application proposed for auto reinforcement made of BR1500HS steel.
4 Process Parameters Optimization 4.1 Hammersley Sequence SamplingThe difficulty of optimization problems lies in the complexity of the search space. Generally, the traditional optimization generates initial population by uniform random sampling. Unfortunately, the random sampling techniques often cause many questions, for instance, over-sampling in some areas and sparse sampling in others. Therefore, the initial population generated from random sampling has low uniformity.
One approach developed to address this problem is Latin Hypercube Sampling (LHS). Due to practical application employed by the Latin Hypercube Sampling (LHS) method, its uniformity and diversity is not satisfactory.Therefore, an alternative approach is investigated.
Hammersley Sequence Sampling (HSS) is to use quasi-random or low discrepancy sequences[16]. The low discrepancy sequence is less random than a pseudo-random number sequence, but it tends to sample search space more uniformly than random numbers.
The uniformity properties of above three sampling techniques are compared as shown in Fig. 5. In detail, it shows the 100 points on a unit square generated respectively using current uniform random sampling, LHS and HSS. The sample points generated by HSS are more uniform than others. Hence, HSS are preferred techniques for generating initial population.
Since two design variables were chosen, namely initial forming temperature (x1(℃)) and blank holder force value (x2(kN)), a two dimensional optimization problem was managed: twenty-five simulations were enough for this kind of problem with HSS sampling technique.Each combination of the design variables will be used for the finite-element analysis to obtain the forming quality indices' values- maximum thinning (t(%)). The results of the samples for the chosen HSS sampling technique are presented in Table 2.
| Table 2 Design variables and objective function value |
4.2 BP-GA Step
Artificial neural networks are a large class of parallel processing architectures, which can mimic complex and non-linear relationships through the application of many non-linear processing units called neurons[17]. It has been proved that a neural network with back propagation algorithm, consisting of three layers (namely input, hidden and output), can map any non-linear relationship with a desired degree of accuracy[18]. However, BP neural network is prone to getting into local extreme and convergence is slow. To overcome these drawbacks, this study attempts to combine genetic algorithm (GA), avoiding local minima and achieving global convergence quickly. GA is an optimization and search technique based on the principles of genetics and natural selection. Generally, in the present paper, a BP neural network model is developed to obtain the mathematical relationship between optimization goal and design variables. The model obtained from BP neural network is used as the objective function for the minimization of the forming quality indices’ values (t(%)) using the genetic algorithm. The above described BP-GA workflow procedure is illustrated in Fig. 6.The mixed algorithm is divided into BP segment and GA segment. Each step of the BP-GA mixed algorithm is explained as follows.
(1) Using the HSS technique to generate initial population.
(2) Developing a BP neural network model to obtain the mathematical relationship between optimization goal and design variables.
(3) Evaluation of the accuracy of the obtained BP neural network model in terms of error of the predictions provided by it with respect to the actual numerical values. If the error is small, the model will be better.
(4) The best model obtained from BP neural network is used as the fitness function for the minimization of the forming quality indices' values (t(%)) using the genetic algorithm. Section 4.4 will describe in detail the steps of the above illustrated GA segment with particular reference to a real application.
4.3 Training and Testing of Neural NetworkIn order to avoid an over-fitting, it is a common practice to divide the experimental data into two sets (training dataset and testing dataset) in manufacturing field[19]. Simulation numbers S4, S5, S11, S14 and S17 in Table 2 are randomly selected to test the network, and the other 20 sets of data are utilized as training set. Before training, it is often useful to scale the inputs and targets so that they always fall within a specified range. The function mapminmax scales inputs and targets so that they fall in the range [-1, 1]. As for the choice of the learning algorithm, the Levenberg-Marquardt (LM) algorithm which is designed to avoid the calculation of the Hessian matrix are employed for training of the network.
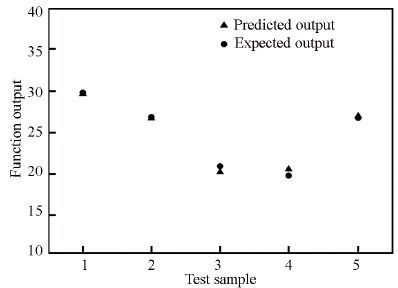
The training procedure of the network is programmed and the expectation mean square error is designated as 0.000 1. Fig. 7 depicts a good agreement between the predicted outputs and the expected outputs. Consequently, we can conclude that the model obtained from BP neural network canexactly approximate the actual response of the system.
|
Figure 7 Comparisons between the predicted outputs and the expected outputs for testing samples |
4.4 Genetic Operation
GA has been proved to be capable of finding global optima in complex problems by exploring virtually all regions of the state space and exploiting promising areas through mutation, crossover and selection operations applied to individuals in the populations[20]. The parameters used for GA are as follows: population size=20, termination generation=100, crossover probability=0.4 and mutation probability=0.2.A genetic algorithm processes the populations of chromosomes by replacing unsuitable candidates according to the fitness function[21].
The flowchart of genetic algorithm has already been shown in Fig. 8. As GA segment of the procedure is concerned, some details on the genetic algorithm are given in the following.
|
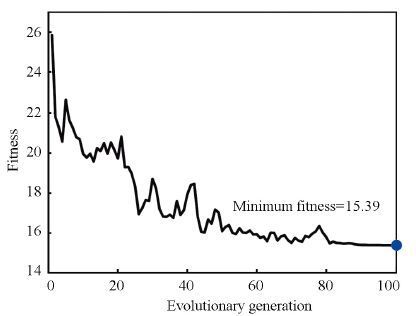
Figure 8 Fitness curve |
(1) Fitness Evaluation:GA uses fitness function to evaluate the viability of the chromosome.In this study, the fitness value is the thickness reduction ratio.Thus, the smaller the fitness value is, the better the hot forming quality is.
(2) Selection:the extremely important step in GA is the selection.Selection is based on the fitness of each individual.In this paper, the roulette wheel selection is employed, which is the most common way.A probability will be evaluated for each individual.The roulette wheel selection method can be formulated as follows:
| ${{F}_{i}}=-\frac{{{f}_{i}}}{\sum\limits_{i=1}^{N}{{{f}_{i}}}}$ |
where Fi is the probability evaluated for each individual i.The fitness of individual i is denoted by fi and N is the size of the population. We select the most fitness individual to continue genetic manipulation.
(3) Recombination and mutation:In this paper, the cross usesthe method of arithmetic crossover, and variationmethod usesthe operation of nonuniform mutation.
(4) The process will be accomplished when we get appropriate fitness or evolution has completed the default maximum number of generations.
The optimum forming temperature and blank holder force value is found to be 770.42 ℃and 247 kN respectively with minimum fitness value of 15.39. The optimum max-thinning is far below the allowable thinning in industry (20 %). The final result as it is represented by a curve plot shown in Fig. 8, using the optimization procedure above to find the optimum parameters, the formability of the sheet metal is improved and the likelihood of cracking is reduced.
4.5 Stamping Test VerificationTo demonstrate the validity of the forming analysis and the optimization, the stamping experiment is carried out, as shown in Fig. 9.According to the optimal process parameters(blank temperature of 770.42 ℃, blank-holder forces of 247 kN), the auto reinforcements are drawn successfully, which indicates that the feasible region of the parameters and optimization method are correct and reliable.

|
Figure 9 Forming parts after optimization |
We know that the thickness reduction ratio of the stamping part is an important forming quality index in this study. Therefore, the difference of the thickness reduction ratio between the actual test and the numerical simulation must be investigated. Fig. 10 shows that the thickness reduction ratio, which is used in the optimal finite-element model, along two dangerous sections differs from that of the actual part. The tendency of the thickness reduction ratio to vary is the roughly the same based on the finite-element and stamping test results.

|
Figure 10 Thickness reduction ratio along dangerous sections |
To reveal the microstructure evolution, we performed metallographic tests of the point on the fillet area (①-②), as shown in Fig. 11. As seen, the metallograph revealed that martensite appeared as a lath shape for the material, which is the reason for the high tensile strength of HSS under the hot stamping process. Meanwhile, tests on tensile strength and hardness were performed to a quantitative tool to study mechanical properties of the final product. The mean values of the experimental hardness and tensile strengths 450 HV and 1 500 MPa, respectively.

|
Figure 11 Final microstructure evolution of fillet areas after forming process |
5 Conclusions
(1) The trend predicted by simulation matches well with experiment.It is proved that finite element analysis method can successfully capture the deformation modes and the specific characteristics of the hot sheet stamping process by combing the material model with an elastic visco-plastic material code (MAT-106 in LS-DYNA)that account for temperature dependent properties.
(2) The integration of HSS strategy and BP-GA mixed algorithms is capable of accurate prediction on forming quality of the products, which is applied for the design of the initial blank temperature and blank holder force. The validation of the final results using an explicit industrial code shows that the proposed optimization algorithms are well suited for hot stamping process design.
| [1] |
Jeon Y J, Song M J, Kim H K, et al. Effect of hot-stamping process conditions on the changes in material strength.
International Journal of Automotive Technology,2015, 16 (4) : 619-627.
( 0) 0)
|
| [2] |
Choi H S, Nam K J, Lim W S, et al. The optimization of hot press bending for improving dimensional accuracy and mechanical strength of bent product.
Metals and Materials International,2010, 16 (6) : 1001-1007.
( 0) 0)
|
| [3] |
Mori K, Maki S, Tanaka Y. Warm and hot stamping of ultra high tensile strength steel sheets using resistance heating.
Cirp Annals-Manufacturing Technology,2005, 54 (1) : 209-212.
( 0) 0)
|
| [4] |
Maikranz-Valentin Manuel, Weidig Ursula, Schoof Ulrich. Components with optimised properties due to advanced thermo-mechanical process strategies in hot sheet metal forming.
Steel Research International,2008, 79 (2) : 92-97.
( 0) 0)
|
| [5] |
Cui J J, Sun G Y, Xu J R, et al. A method to evaluate the formability of high-strength steel in hotstamping.
Materials & Design,2015, 77 : 95-109.
( 0) 0)
|
| [6] |
Hu P, Shi D Y, Ying L, et al. The finite element analysis of ductile damage during hot stamping of 22MnB5 steel.
Materials & Design,2015, 69 : 141-152.
( 0) 0)
|
| [7] |
Kitayama S, Yoshioka H. Springback reduction with control of punch speed and blank holder force via sequential approximate optimization with radial basis function network.
International Journal of Mechanics and Materials in Design,2014, 10 (2) : 109-119.
( 0) 0)
|
| [8] |
Hoffmann H, So H, Steinbeiss H. Design of hot stamping tools with cooling system.
Cirp Annals-Manufacturing Technology,2007, 56 (1) : 269-272.
( 0) 0)
|
| [9] |
Ingarao G, Di Lorenzo R, Micari F. Analysis of stamping performances of dual phase steels: A multi-objective approach to reduce springback and thinning failure.
Materials & Design,2009, 30 (10) : 4421-4433.
( 0) 0)
|
| [10] |
Zhou Jing, Wang Baoyu, Lin Jianguo. Optimization of an aluminum alloy anti-collision side beam hot stamping process using a multi-objective genetic algorithm.
Archives of Civil and Mechanical Engineering,2013, 13 (3) : 401-411.
( 0) 0)
|
| [11] |
Martin Meckesheimer, Booker A J. Computationally inexpensive metamodel assessment strategies.
Aiaa Journal,2002, 40 (10) : 2053-2060.
( 0) 0)
|
| [12] |
Preechakul C, Kheawhom S. Modified genetic algorithm with sampling techniques for chemical engineering optimization.
Journal of Industrial and Engineering Chemistry,2009, 15 (1) : 110-118.
( 0) 0)
|
| [13] |
Hoffmann H, So H, Steinbeiss H. Design of hot stamping tools with cooling system.
CIRP Annals-Manufacturing Technology,2007, 56 (1) : 269-272.
( 0) 0)
|
| [14] |
Shang Xin, Zhou Jie. Research on thermo-deformation and formability in the hot stamping of BR1500HS.2012 Postdoctoral Symposium of China on Materials Science & Engineering Advanced Materials for Sustainable Development, 2012.276-276.
( 0) 0)
|
| [15] |
Wu P D, Graf A. On forming limit stress diagram analysis.
International Journal of Solids and Structures,2005, 42 (8) : 2225-2241.
( 0) 0)
|
| [16] |
Diwekar U M, Kalagnanam J R. Efficient sampling technique for optimization under uncertainty.
AIChE Journal,1997, 43 (2) : 440-447.
( 0) 0)
|
| [17] |
Ambrogio G, Filice L, Guerriero F, et al. Prediction of incremental sheet forming process performance by using a neural network approach.
International Journal of Advanced Manufacturing Technology,2011, 54 (9-12) : 921-930.
( 0) 0)
|
| [18] |
Hornik K. Multilayer feedforward networks are universal approximators.
Neural Networks,1989, 2 (5) : 359-366.
( 0) 0)
|
| [19] |
Sukthomya W, Tannock J. The optimization of neural network parameters using Taguchi's design of experiments approach:An application in manufacturing process modelling.
Neural Computing and Applications,2005, 14 (4) : 337-344.
( 0) 0)
|
| [20] |
Hardala N, Ercan N, Hardalac F, et al. Classification of educational backgrounds of students using musical intelligence and perception with the help of genetic neural networks.
Expert Systems with Applications,2009, 36 (PART 2) : 6708-6713.
( 0) 0)
|
| [21] |
Fu Zemin, Mo Jianhua, Chen Lin, et al. Using genetic algorithm-back propagation neural network prediction and finite-element model simulation to optimize the process of multiple-step incremental air-bending forming of sheet metal.
Materials & Design,2010, 31 (1) : 267-277.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


