Surface electromyography (sEMG) signal is a kind of the electrical activity generated during muscular contractions. Efficient recognition of human multi-movement patterns using sEMG has attracted research interests in human machine interaction and rehabilitation engineering fields during the past three decades [1-2]. Researchers have identified sEMG-based movements about upper limb including arm, wrist and gross hand movements with high recognition accuracies[3-4].However, it is a challenging task to recognize subtle hand movements, such as individual finger and multi-finger movements, with the high accuracies. It is because most of forearm muscles are small muscles. Besides, the same muscle contracts when we perform two different movements, which leads to the similarity between two movements. The similar movements are identified with lower recognition accuracies. The pattern-recognition-based strategy has been proposed to recognize multi-movement patterns. Hargrove et al.[5]had found that the features extracted from sEMG are more crucial than the classifiers for the recognition performance. This paper focused on extracting the features with optimal class separability from sEMG to improve the recognition accuracies of subtle hand movements.
The time, frequency and time-frequency processing methods have been widely used to extract sEMG features for movement classification [6-8]. The sEMG signal is assumed as a short-time stationary signal in both time and frequency domains. Studies have indicated the potential non-stationarity in sEMG signal affects the performance of movement recognition[9].Therefore, the time and frequency methods have their limitations to represent the sEMG signal.The wavelet transform and wavelet packet transform (common time-frequency methods) work well in analyzing the non-stationary signals. However, they do not lead to sparse decompositions (i.e., with very few nonzero decomposition coefficients), so the time-frequency resolution is not very high.Thus the features with good class separability cannot be extracted using the time-frequency methods.
This paper introduced sparse representation [10] to feature extraction of non-stationary sEMG signal.Studies have shown sparse representation is applicable for analyzing the non-stationary signals [11].Sparse representation can analyze the non-stationary sEMG with high time-frequency resolution.Many natural signals tend to be compressible rather than sparse and the sEMG signal is compressible in some transformed domains [12].The nonzero decomposition coefficients represent the sEMG signal with maximum efficiency.They may be considered as the sEMG features. In addition to the wavelet analysis, some other methods for sparse representation are not exploited widely for feature extraction of sEMG signal [13].In most recent study, Naik et al.[13] have introduced non-negative matrix factorization (NMF), a sparse representation method, to classify finger flexion movements. Studies have shown sparse Bayesian learning (SBL) algorithm is well suited for finding maximally sparse representation [14].This property makes SBL valuable to extract the features with good separability from sEMG signals. Literature search indicates that there is no published investigation on the analysis of SBL for the sEMG-based application of movement recognition. Temporal Multiple Measurement Vector Sparse Bayesian Learning (T-MSBL) is an improved SBL algorithm[15].This paper employed T-MSBL to extract effective features from sEMG for multi-movement recognition.
2 Sparse Reconstruction Modeling of sEMGSparse representation of sEMG is to find a linear combination of a minimum number of atoms from an over-complete dictionary to approximate the original signal.
| $\begin{align} & \hat{\rho }=\underset{\rho }{\mathop{argmin}}\, \left( \left\| z-G\rho \right\|_{2}^{2}+\xi \upsilon \left( \rho \right) \right) \\ & s.t. \\ & z=G\rho +\varepsilon \\ \end{align}$ | (1) |
Where z∈Rd×1 is the sEMG signal;G∈Rd×K(K>d) is the over-complete dictionary; ρ∈RK×1 is the vector of sparse coefficients; υ(ρ) is sparsity constraint item; ζ(ζ>0) is the balance parameter between ‖z-Gρ‖22 and υ(ρ) ;ε is the modeling errors; z and ρ are equivalent representations of sEMG signal. Nonzero entries in
One of the major challenges for the common sparse representation algorithms is the high computational cost and large memory capacity. So we also introduce compressed sensing (CS) [16] theory into the feature extraction scheme of sEMG to alleviate the problem. The original sEMG signals are first mapped to lower dimensional domain using CS. Then representation coefficients are estimated by solving convex optimization problems. Assuming that sEMG signal s∈Rd×1 is compressible in transform domain D, i.e., s=Dρ. The sparse reconstruction modeling of the sEMG signal can be described as follows.
| $y=\Theta s+e=\Theta D\rho +e=A\rho +e$ | (2) |
Where Θ∈Rc×K is a c×K measurement matrix (c <K);D∈RK×K is the dictionary matrix for sparse representation and assume that the basis is orthonormal for simplicity; A∈Rc×K is written as A=ΘD ;ρ∈RK×1 is sparse coefficients of s over the dictionary D; y∈Rc×1 is the vector of the compressed measurements in the low dimension space.
3 T-MSBL AlgorithmSparse Bayesian Learning (SBL) algorithm uses the prior to promote the sparsity of signal to the largest extent. It is equivalent to an algorithm of iterative reweighted L1-norm minimization. Studies have shown that iterative reweighted algorithms obtain more sparse solutions than conventional algorithms do [14]. T-MSBL algorithm is mainly used to solve multiple measurement vectors (MMV) problem. It can be also suitable to solve single measurement vector (SMV) problem. Under this circumstance, the T-MSBL algorithm, like other SMV algorithms, only exploits the sparsity of the solution matrix. But this algorithm can provide better performance than other SMV algorithms do.
The MMV model is given by
| $Z = \Psi P + E$ | (3) |
Where Z∈Rd×L is a measurement matrix consisting of L measurement vectors and P∈RK×Lis an unknown coefficient matrix which has only a few nonzero rows. Ψ∈Rd×K is mapping matrix. The key assumption in T-MSBL is that each row Pi satisfies a parameterized Gaussian distribution:
| $p\left( {{P}_{i}};{{\gamma }_{i}}, {{B}_{i}} \right)\sim N\left( 0, {{\gamma }_{i}}{{B}_{i}} \right), i=1, 2, ..., N$ | (4) |
Where γi and Bi are hyperparameters. γi is a nonnegative scalars controlling the row sparsity of P. When γi=0, the i- th row element Pi becomes 0. Most γi tend to very small values because of the mechanism of automatic relevance determination. Those γi which tend to very small values are set to 0 using a threshold in T-MSBL. Bi is a positive definite matrix capturing the temporal correlation structure of Pi, which is adaptively learned from the sEMG data.
To conveniently derive T-MSBL, by letting z=vec(ZT)∈RdL×1, G=Ψ⊗IL, ρ=vec(PT)∈RKL×1, ε=vec(ET), the MMV model (see Eq. (3)) is equivalently transformed to the single vector model, i.e., z=Gρ+ε(see Eq. (1)). Assuming each element in ε has a Gaussian distribution p(ε;λ)~N(0, λI), where λ is variance. According to the Bayes rule, the posterior probability p(ρz;Γ) is written as p(ρz;Γ)=N(μ, Σ). The mean μ and the covariance matrix Σ are given by
| $\mu =\frac{1}{\lambda }\Sigma Gz$ | (5) |
| $\begin{align} & \Sigma =\left( \Sigma _{0}^{^{-1}}+\frac{1}{\lambda }{{G}^{T}}G \right)-1= \\ & {{\Sigma }_{0}}-{{\Sigma }_{0}}{{G}^{T}}{{\left( \lambda I+G{{\Sigma }_{0}}{{G}^{T}} \right)}^{-1}}G{{\Sigma }_{0}} \\ \end{align}$ | (6) |
Where Γ is the set of all the hyperparameters {λ, γi, Bi};Σ0is given by Σ0={diagγiBi, ..., γNBN}. After the hyperparameters are estimated, the estimate of ρ, i.e.,
The sEMG signals were acquired using the MP150 system (BIOPAC Systems Inc., USA) with a band-pass filter within 10-500 Hz. The sampling frequency was 1 000 Hz. The signals were collected by disposable Ag/AgCl ECG electrodes with conductive paste. Six human hand/finger movements were planned to classify:1) thumb extension (EXTF), 2) index extension (EXIF), 3) thumb flexion (FLTF), 4) palm extension (EXPM), 5) HOOK and 6) OKAY, as shown in Fig. 1. The subtle movements selected in this study were common, polite and easy to perform in our daily lives. We considered not only mutually opposite movements (e.g., EXTF and FLTF), but also similar movements (e.g., EXIF and HOOK, EXPM and OKAY) to further complicate the movement recognition. Four channels of sEMG signals were collected. According to human anatomy, four pairs of electrodes were pasted over extensor pollicis brevis (EPB), flexor pollicis longus (FPL), extensor indicis proprius (EIP) and extensor digitorum (EDM), respectively [17]. The muscle positions for the electrode locations are generally used for the recognition of the six movements[18].The skin areas where the electrodes were attached were degreased beforehand with 95% medicinal alcohol. The pair of electrodes had a center-to-center spacing of 15 mm.
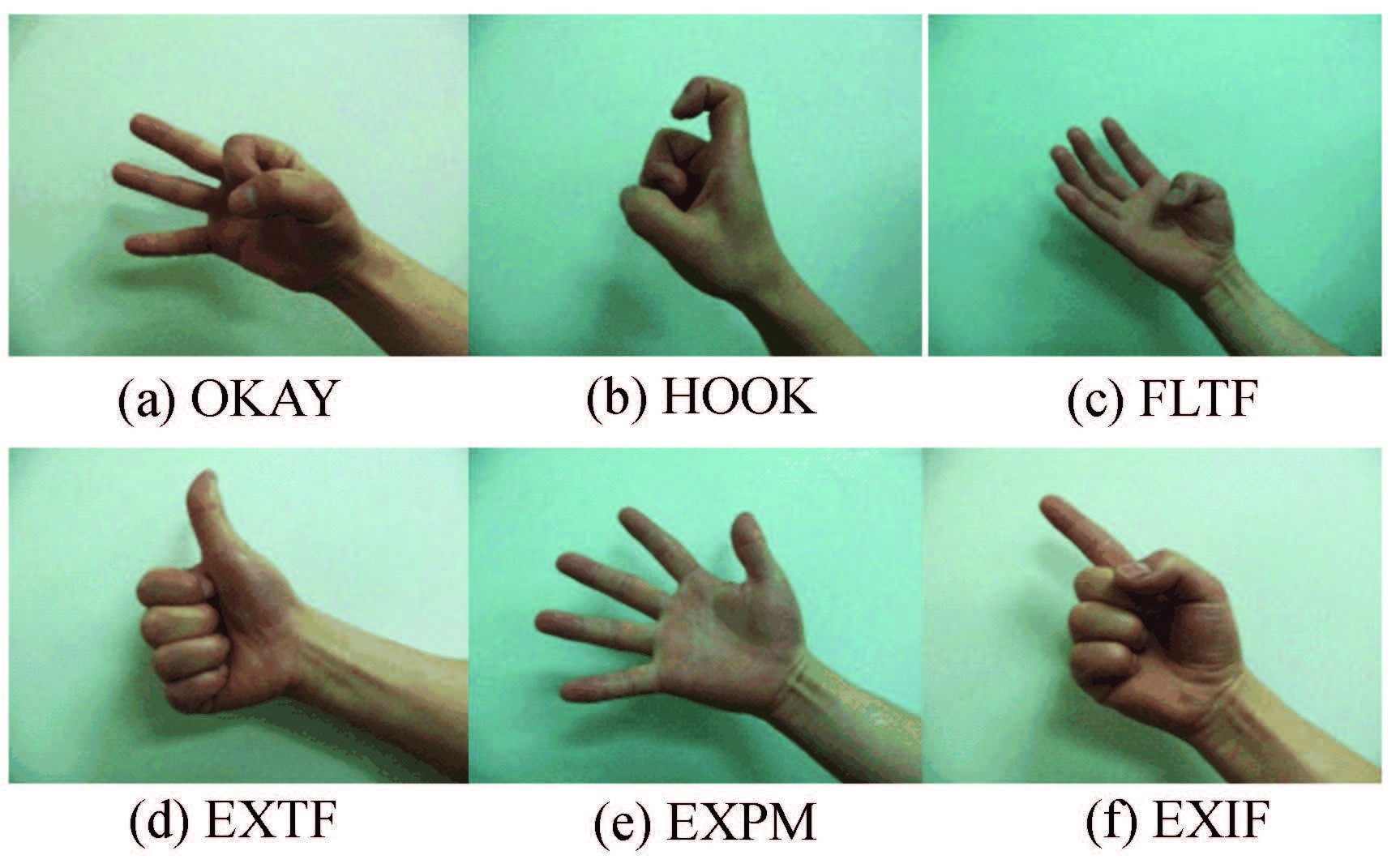
|
Figure 1 Six classes of hand and finger movements |
Twelve able-bodied subjects (six females and six males, aged 20 to 28 years) participated in our experiment. All subjects had signed their written informed consent. Beihang University ethics committee approved the study protocol. Each subject was conducted to perform twenty groups of the above six classes of movements. Each movement was repeated ten times in each group. Each movement was held for 2-3 s. The interval of adjacent movements in each group was 3 s. The subjects should relax their hands during the interval. The subjects should wait at least two hours before the next group to avoid muscle fatigue. Steady-state sEMG data were analyzed to discriminate the different movements. The data were segmented by the analysis window to extract the features.The response of system should be less than 300 ms for reducing users’ perceived lag [6].Therefore, the analysis window was set to 256 ms sliding (one segment) with a 128 ms window increment. For the twenty groups of collected data, training and testing of one classifier were implemented using leave-one-out cross-validation.
4.2 Feature Extraction
According to Section 2 and Section 3, s was the raw sEMG signals generated by a certain movement, K was the length of each segment of signal and K=256.To compress the sEMG signals segment by segment, a sparse binary matrix of the size 128×256 was used as the measurement matrix Θ. Each column of Θ contained only a few entries equal to 1 with random locations, while other entries were 0. The optimal signal approximation depends on the selection of dictionary.However, heavy computation for selecting the best dictionary becomes an obstacle in application. The sEMG signal is compressible in some wavelet bases. Therefore wavelet bases are chosen as dictionary matrixes to balance computation and practical application. The shapes of some wavelets in Daubechies family are similar to single motor action unit potential (MUAP) [19]. We chose Daubechies (order of 6) wavelet as the dictionary matrix D. The dictionary D had the size of 256×256. The compressed data of each segment y was obtained using y=Θs. The T-MSBL algorithm calculated the estimate of ρ (i.e.,
If sparse coefficients were directly used as the input vectors of classifier, we would not achieve satisfying recognition results and heavy computing cost was also involved. Hence the statistical features of the decomposition coefficients were taken as feature vectors. Mean absolute value (MAV) and root mean square (RMS) of the decomposition coefficients were used for classification. The MAV value ωrc and RMS δrc value were calculated as follows:
| ${{\omega }_{rc}}=\frac{1}{M}\sum\limits_{l=1}^{M}{\left| \rho \left( l \right) \right|}\text{ }, {{\delta }_{rc}}=\frac{1}{M}\sum\limits_{l=1}^{M}{{{\rho }^{2}}\left( l \right)}$ | (7) |
Where ρ is the sparse coefficient vector in each analysis window;M is the number of nonzero entries of ρ.
5 Experiments and DiscussionThe proposed feature of sparse representation coefficients (SRC) was used to recognize the six classes of movements. The recognition performance of SRC feature was compared with those of some common features. The common features in our work were:mean absolute value (MAV), root mean square (RMS), waveform length (WL), zero crossing (ZC), slope sign changes (SSC), integrated EMG (IEMG), histogram of EMG (HEMG), Williston amplitude (WAMP), AR coefficients (ARC), median frequency (MDF), frequency-band energy ratio after wavelet decomposition (ERA), root mean square extracted from the NMF separated signals (NMF1) and auto regressive coefficients extracted from the NMF separated signals (NMF2)[20]. The recognition performance was quantified by recognition accuracy (RA). Two experiments were performed to validate the feasible of the proposed feature extraction scheme.
5.1 Performance Comparison of Single EMG FeaturesWe realized movement recognition by SVM classifier in the first experiment. The average RA results with different single features are shown in Table 1.
| Table 1 The mean/std recognition results of different single features |
As shown in Table 1, the SRC has the highest average RA (85.92%) among all the single features, while the HEMG has the lowest one (64.65%). The features of ERA and NMF2 have better accuracy, which are 85.83% and 85.60%, respectively.The features of AR4, WL and WAMP have comparable recognition performance, whose accuracies are over 84.50%. The features of IEMG, ZC and SSC have relatively lower RA results. Most features in the time domain and frequency domain cannot represent the non-stationary sEMG signals exactly. Hence their average RA results are unsatisfactory. The algorithms of wavelet and NMF can make the signal representation sparse to some certain extent. However, the sparseness of the results from wavelet decomposition and NMF is rather weak. Hence the features of ERA and NMF2 just offer the mean RAs of 85.83% and 85.60, respectively. The T-MSBL algorithm is equivalent to an iterative reweighted L1 minimization algorithm. Hence the global minima of T-MSBL are always the sparsest solution[15].Compared to the other single features, the feature SRC provides more inherent information in sEMG and greater class-separating capability. So the feature SRC gets the best RA result. The orthogonal wavelet base was adopted to analyze the sEMG signals because of the complexity of signals in this study. The optimal sparse solutions over predefined orthogonal wavelet base might not be obtained. Hence the feature SRC has no huge advantage over other single features. We can consider the multi-features combining different single features to classify different movements in the next section.
Some criteria, such as Euclid-distance, entropy, and Fishers linear discriminate index (FLDI), can quantitatively assess the separability of sEMG features[20]. The FLDI represents clusters’ dispersion comparing to their scatter[20].A larger FLDI value means a higher possibility of linearly discriminating the clusters in the feature space.Fig. 2 shows the FLDI values of different single features. The trend of the FLDI values demonstrates that the separability of SRC is superior to those of other single features.
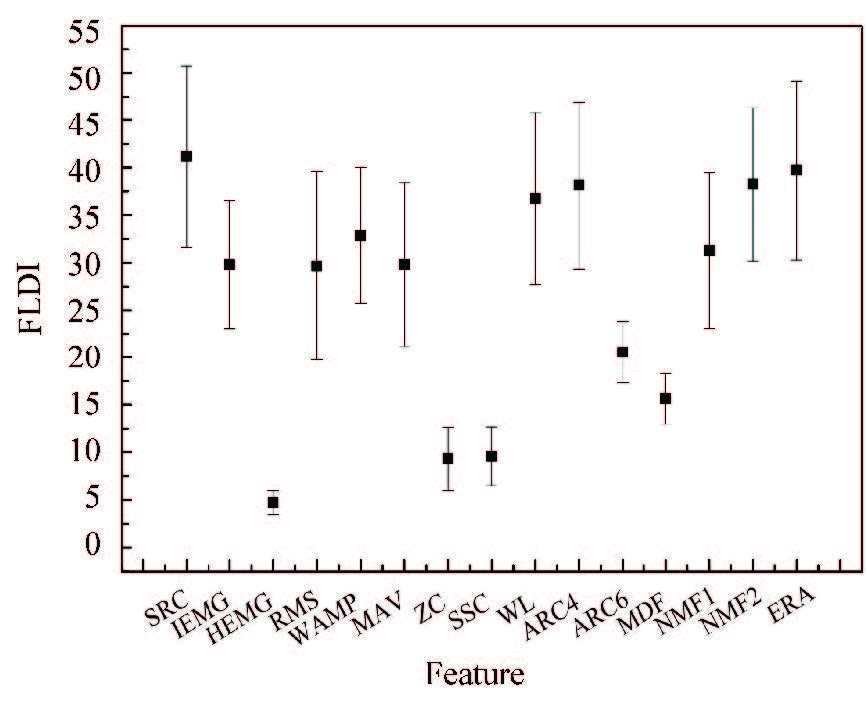
|
Figure 2 The FLDI values of different single features |
Fig. 3 displays the recognition results for six movements using the feature SRC and SVM classifier. According to the results in Fig. 3, the movements of gross hand and individual finger, such as EXPM, FLTF, EXTF and EXIF, are easily recognizable.Their average RA results are over 85%.The movements with more fingers may cause confusion and be misidentified.The multi-finger movements which are similar to the other ones have lower RA results among all movements.HOOK is misclassified as EXIF and OKAY is misclassified as EXPM.The possible reasons for misidentification include measurement conditions, physiological structures of forearm muscles, etc.Regarding the results in Fig. 3, it can be due to the similarity between two movements.For example, extensor indicis proprius (EIP) served a similar contractile function when we performed the movement HOOK and EXIF, respectively.
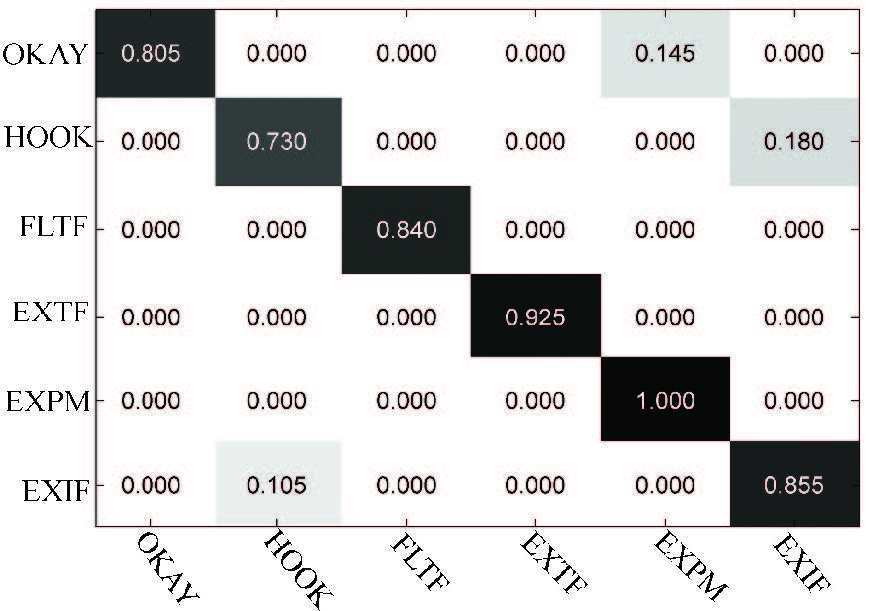
|
Figure 3 Recognition results for six movements using the feature SRC and SVM classifier |
5.2 Comparison of Recognition Performance Among Multi-Feature Sets
The multi-motion recognition with a single feature makes it difficult to obtain a satisfactory RA result. Studies have proved that the recognition performances of multi-feature sets are much better than those of the single features [21-22]. If the single feature constituting a multi-feature set has no correlation to the others (i.e., they are all independent of each other), the RA result of the multi-feature set can be improved greatly. The multi-feature sets constituted by the single features in Section 5.1 were employed in the second experiment. We classified the six movements with these multi-feature sets and SVM classifier. The RA results are shown in Fig. 4. The possible number of multi-feature sets was so large that we could not show all combinations here. The multi-feature sets whose RA results were good are shown in Fig. 4. The multi-feature sets with poor RA results are not shown.
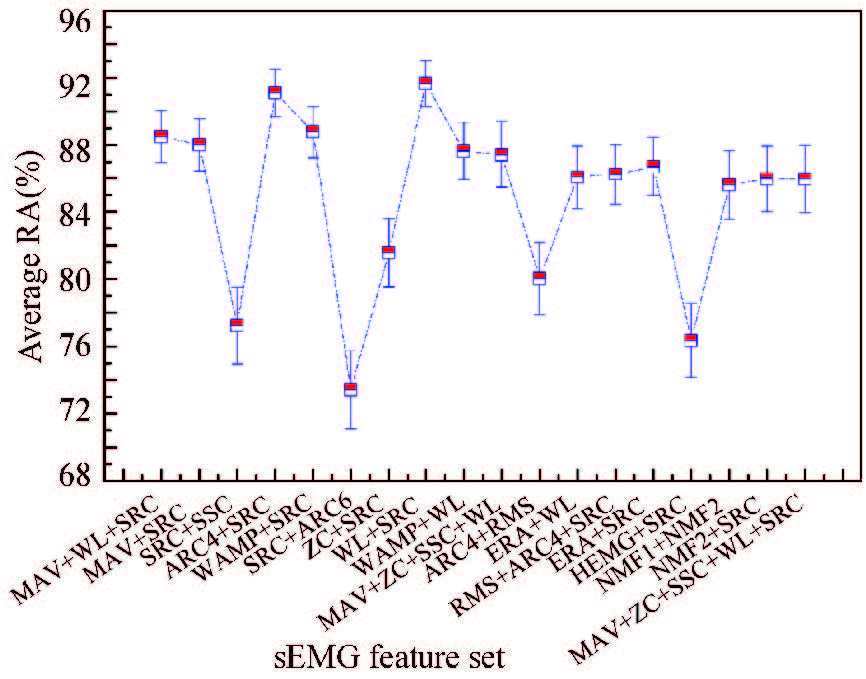
|
Figure 4 The mean/std recognition accuracies of different feature sets |
According to the results in Fig. 4, the multi-feature sets obtain more satisfying and more stable performance than the single features do. The average RA results of multi-feature sets, such as MAV+WL+SRC, MAV+SRC, AR4+SRC, WAMP+SRC and SRC+WL, are more than 88%. The multi-feature set SRC+WL has the best RA result, 91.67%, among all multi-feature sets. The RA result of SRC+ARC6 is the lowest. Not every multi-feature set achieves better RA result than the single feature from the same multi-feature set. For example, RMS has the RA result of 81.84% and ARC4 has the RA result of 85.48%, as displayed in Table 1. However, the RA result of the multi-feature set, RMS+ARC4, is only 80.03%. A possible reason for this is that the multi-feature set RMS+ARC4 has correlation with the single feature RMS or ARC4. It makes the class separability of RMS+ARC4 worse.
Fig. 5 displays the FLDI values of different multi-feature sets.The trend of the FLDI values demonstrates that the separability of SRC+WL is superior to those of other multi-feature sets.
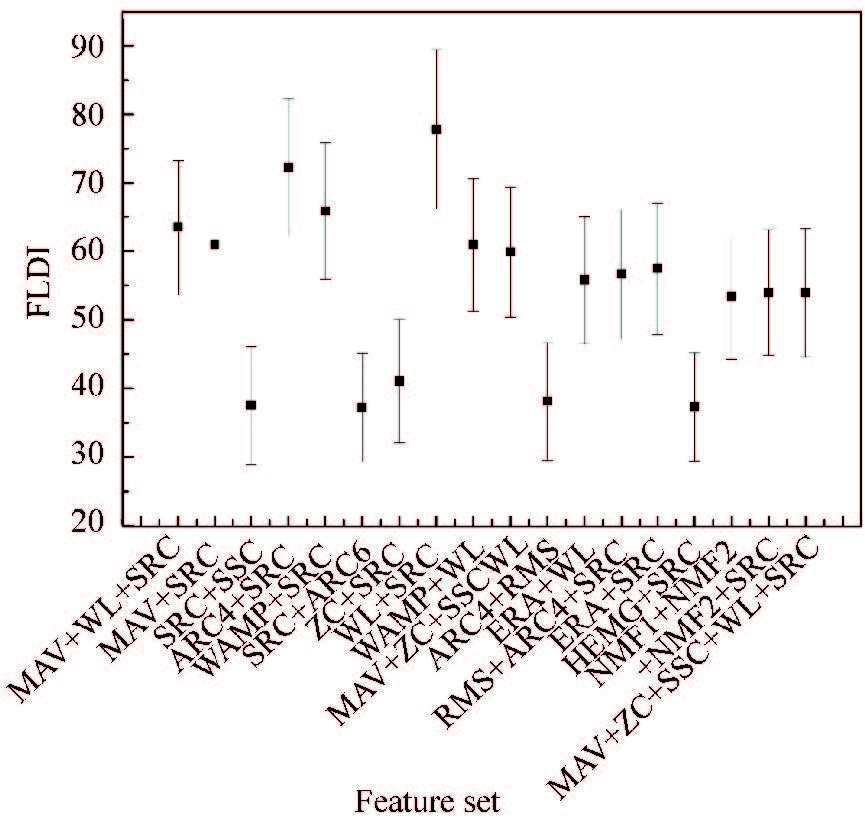
|
Figure 5 The FLDI values of different multi-feature sets |
Fig. 6 presents the recognition results for the six movements using the multi-feature set SRC+WL and SVM classifier. The results indicate that the multi-feature set SRC+WL achieves high recognition performance in movement classification. The average RA results of six movements using SRC+WL are improved greatly when compared with the results shown in Fig. 3. The movements of EXTF and EXPM have the average RA results of greater than 95%.The average RA results of EXIF and FLTF are over 92%. The average RA result of OKAY increases from 80.50% to 85.50% and the average RA result of HOOK increases from 73.00% to 81.00%. The results demonstrated that the combined features have more superior performance when compared with the single features.
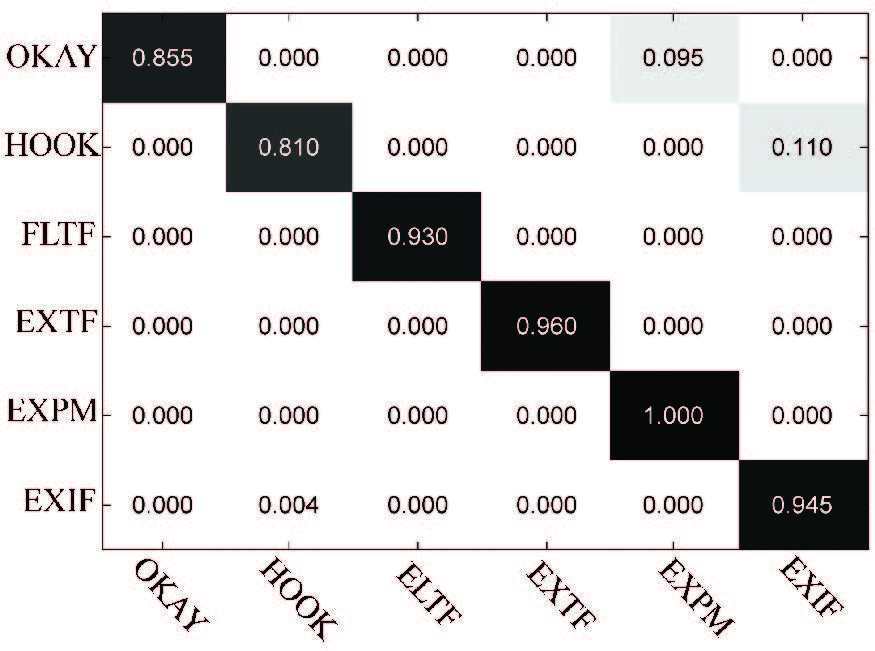
|
Figure 6 Recognition results for six movements using the multi-feature set SRC+WL and SVM classifier |
We had assessed the performance of the features including multi-feature sets and single features using SVM classifier. Now all the sEMG features mentioned above were evaluated using different classifiers. The following results would demonstrate that the effect of different classifiers on recognition performance was not significant when the extracted features were more distinguishable than other features. We focused more on the features with better performance. So we chose the top five multi-feature sets to access the performance. They were WL+SRC, ARC4+SRC, WAMP+SRC, MAV+WL+SRC and MAV+SRC. Four common classifiers, k-nearest neighbor (k-NN), linear discriminant analysis (LDA), multi-layer perceptron (MLP) and SVM were employed. The recognition results are shown in Fig. 7.
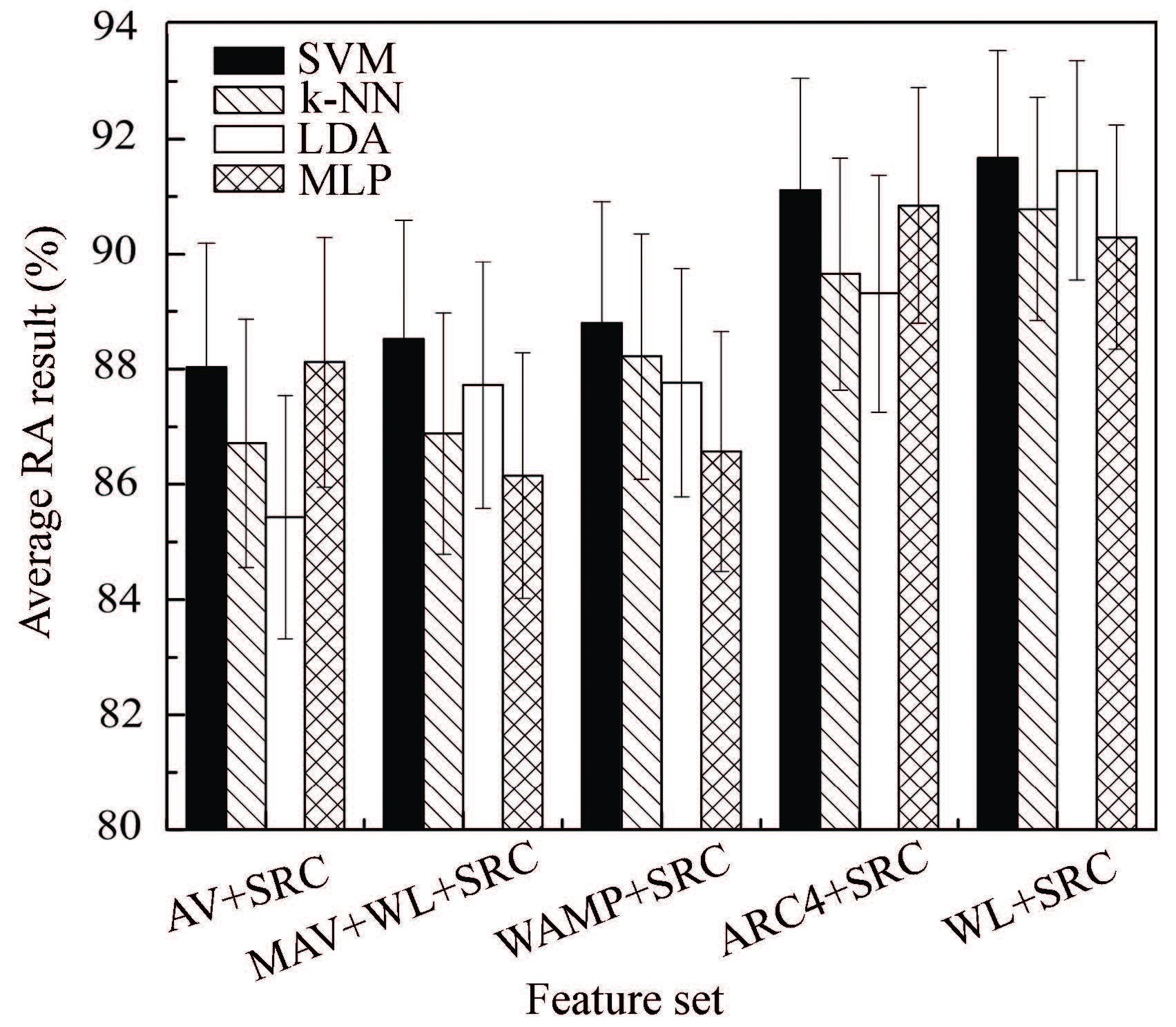
|
Figure 7 The recognition accuracies of five multi-feature sets using different classifiers |
The results in Fig. 7 show that the multi-feature set WL+SRC has the better accuracy for all five classifiers when compared with other feature sets. The best RA result is gained by using WL+SRC and SVM among all the features and classifiers. But the distinctions among the accuracies of four classifiers with the same multi-feature set are less sharp. It is testified that different classifiers have no significant effect on the RA results when more distinguishable features are extracted.
We used the analysis of variance (ANOVA) method to determine the effect of sEMG features and classifiers on the RA results. The α value of the feature factor was 0 (α<0.05) in this study. The α value of the classifier factor was 0.31 (α >0.05). The results indicated the features take significant effect on the RA results, while the effect of classifiers is not significant. These results are consistent with the previous results in Refs.[21-22], which have indicated the effect of features plays a more crucial role than that of classifiers in recognition performance.Bonferroni multiple comparison analysis further indicated that the RA result of WL+SRC differs from those of other features. It shows the performance of WL+SRC is superior to those of other features. We evaluated all the methods of sEMG feature extraction using MATLAB 2010a on a computer with Intel Core i5, 2.3 GHz and 2 GB memory. We reported the run time for each single feature from the multi-feature sets as shown in Fig. 7. The running time for each single feature was 35 ms for SRC, 11 ms for ARC4 and less than 1 ms for MAV, WL and WAMP, respectively. The classifiers ran within 2-4 ms for each feature.
6 ConclusionsThis paper introduced and evaluatedthe SBL approach to extract the features of sEMG signal and to discriminate different types of subtle movements including individual finger and multi-finger movements. The feature SRC was extracted by the T-MSBL algorithm. This feature effectively represented time-varying characteristics of sEMG during movements because of the compressibility of signal in the dictionary. The performance of SRC was compared with a variety of conventional sEMG features in terms of RA and FLDI value. The results demonstrated that the multi-feature set WL+SRC outperformed other 17 multi-features and all single features. The feature set WL+SRC with optimal separability led to the improvement of recognition accuracy and the reduction of false recognition rate for multi-movement recognition. We also found the standard deviation of WL+SRC was relatively small. This suggested that WL+SRC had more robust performance than other features. Moreover, the statistical analysis confirmed that the performance of WL+SRC was superior to those of other features, and feature factor had more significant effect on recognition performance than the classifier factor do. In conclusion, the proposed scheme provided satisfactory performance in terms of recognition results. In the future work, evaluating the proposed scheme on more complex hand movements in daily life will be the focus of our study. Besides, the proposed scheme of feature extraction will be also considered to test on prosthetic hands worn by the amputees.
| [1] |
Khushaba R N, Kodagoda S, Liu D, et al. Muscle computer interfaces for driver distraction reduction.
Computer Methods and Programs in Biomedicine,2013, 110 (2) : 137-149.
( 0) 0)
|
| [2] |
Chan A, Kwok E, Bhuanantanondh P. Performance assessment of upper limb myoelectric prostheses using a programmable assessment platform.
Journal of Medical and Biological Engineering,2012, 32 (4) : 259-264.
( 0) 0)
|
| [3] |
Pang M, Guo S, Song Z, et al. A surface emg signals-based real-time continuous recognition for the upper limb multi-motion. Proceedings of the 2012 IEEE International Conference on Mechatronics and Automation (ICMA). Chengdu, 2012.1984-1989.
( 0) 0)
|
| [4] |
Kim K S, Choi H H, Moon C S, et al. Comparison of k-nearest neighbor, quadratic discriminant and linear discriminant analysis in classification of electromyogram signals based on the wrist-motion directions.
Current Applied Physics,2011, 11 (3) : 740-745.
( 0) 0)
|
| [5] |
Hargrove L J, Englehart K, Hudgins B. A comparison of surface and intramuscular myoelectric signal classification.
IEEE Transactions on Biomedical Engineering,2007, 54 (5) : 847-853.
( 0) 0)
|
| [6] |
Hudgins B, Parker P, Scott R N. A new strategy for multifunction myoelectric control.
IEEE Transaction on Biomedical Engineering,1993, 40 (1) : 82-94.
( 0) 0)
|
| [7] |
Hariharan M, Fook C Y, Sindhu R, et al. A comparative study of wavelet families for classification of wrist motions.
Computers & Electrical Engineering,2012, 38 (6) : 1798-1807.
( 0) 0)
|
| [8] |
Li Y R, Liao Z W, Du M. Analysis of sEMG signal for KOA classification.
Journal of Harbin Institute of Technology (New Seriers),2011 (6) : 113-119.
( 0) 0)
|
| [9] |
Lorrain T, Jiang N, Farina D. Influence of the training set on the accuracy of surface EMG classification in dynamic contractions for the control of multifunction prostheses.
Neuroengineering and Rehabilitation,2011, 8 (1) : 1-9.
( 0) 0)
|
| [10] |
Rubinstein R, Bruckstein A M, Elad M. Dictionaries for sparse representation modeling.
Proceedings of the IEEE,2010, 98 (6) : 1045-1057.
( 0) 0)
|
| [11] |
Wang J, Gao X Z, Guo P. Feature extraction based on sparse representation with application to epileptic EEG classification.
International Journal of Imaging Systems and Technology,2013, 23 (2) : 104-113.
( 0) 0)
|
| [12] |
Balouchestani M, Raahemifar K, Krishnan S. New channel model for wireless body area network with compressed sensing theory.
IET Wireless Sensor Systems,2013, 3 (2) : 85-92.
( 0) 0)
|
| [13] |
Naik G, Nguyen H. Nonnegative matrix factorization for the identification of EMG finger movements: evaluation using matrix analysis.
IEEE Journal of Biomedical and Health Informatics,2015, 19 (2) : 478-485.
( 0) 0)
|
| [14] |
Wipf D, Nagarajan S. Iterative reweighted and methods for finding sparse solutions.
IEEE Journal of Selected Topics in Signal Processing,2010, 4 (2) : 317-329.
( 0) 0)
|
| [15] |
Zhang Z, Rao B. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning.
IEEE Journal of Selected Topics in Signal Processing,2011, 5 (5) : 912-926.
( 0) 0)
|
| [16] |
Donoho D L. Compressed sensing.
IEEE Transactions on Information Theory,2006, 52 (4) : 1289-1306.
( 0) 0)
|
| [17] |
Lu Z N, Zeng Q X, Li C Y, et al.
Practical Electromyography. Beijing: People's Medical Publishing House, 2002 : 499 -509.
( 0) 0)
|
| [18] |
Yang D, Zhao J, Jiang L, et al. Dynamic hand motion recognition based on transient and steady-state EMG signals.
International Journal of Humanoid Robotics,2012, 9 (01) : 1250007-1.
( 0) 0)
|
| [19] |
Sobahi N. M. Denoising of EMG signals based on wavelet transform. Asian Transactions on Engineering.
Asian Transactions on Engineering,2011, 1 (5) : 17-23.
( 0) 0)
|
| [20] |
Phinyomark A, Hirunviriya S, Nuidod A, et al.
Evaluation of EMG feature extraction for movement control of upper limb prostheses based on class separation index. Proceedings of the 5th Kuala Lumpur International Conference on Biomedical Engineering. Berlin: Springer Berlin Heidelberg, 2011 : 750 -754.
( 0) 0)
|
| [21] |
Phinyomark A, Quaine F, Charbonnier S, et al. EMG feature evaluation for improving myoelectric pattern recognition robustness.
Expert Systems with Applications,2013, 40 (12) : 4832-4840.
( 0) 0)
|
| [22] |
Ibrahimy M I, Ahsan M R, Khalifa O O. Design and performance analysis of artificial neural network for hand motion detection from EMG signals.
World Applied Sciences Journal,2013, 23 (6) : 751-758.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


