Constrained optimization problems (COPs) are widely found but difficult to solve in complex real world instances which refer to function optimization[1],image processing[2],network communication[3],etc. Generally constrained optimization algorithms are applied to solve COPs. Effective constrained optimization approaches must be able to deal with constraints as well as converge to global optimum solution.
In general,the studies of COPs mainly include evolutionary algorithms and constraint handling techniques. The traditional global optimization algorithms such as genetic algorithm[4],particle swarm optimization[5],differential evolution algorithm[6],immune clone algorithm[7] must be combined with the constraint handling techniques in order to cope with COPs. Meanwhile,as a very important part of the constrained optimization,constraint handling techniques commonly involve penalty function methods,Deb criterion,stochastic ranking,multi-objective concepts,εconstraint method and so on[8-10]. Runarsson and Yao recommended the stochastic ranking[11] which was the one of the most popular constraint handling techniques,yet it needs to adjust the specific parameter Deb criterion's[12] insufficient use of infeasible solutions which will be not conducive to maintain the diversity of population. Takahama[13] had introduced a ε constraint optimization algorithm which requires a combination of gradient mutation operators to further improve the performance.
The current number of outstanding constrained optimization algorithms has certain limitations due to that the complex constraints cause topological structure of the feasible region to become more complex. Especially for these COPs with some equality constraints and high dimension of decision variable,they are easy to reach local convergence or premature convergence. It demands to enhance the exploration ability and exploitation ability,so diversity and convergence of the population can be coordinated. Therefore,it is urgent to develop more effective method for individual comparison and evaluation. In response to these problems,this paper suggests a constrained optimization algorithm based on double populations. The feasible solutions and the infeasible solutions are respectively deposited in feasible solution set and infeasible solution set. It can prevent direct comparison of feasible solutions and infeasible solutions. Meanwhile,the update mode of infeasible solution set based the novel constraint domination can keep good diversity of the population while taking into account the convergence. On the one hand,the exploration scope can be enlarged through evolution role of infeasible solutions,consequently variety of population will be boosted,on the other hand,unlike other dual populations methods[14-16] usually only preserve the infeasible solution with small constraint violation and rarely consider the synergistic effect of feasible and infeasible solutions,we keep the infeasible solutions whose constraint violation and objective function value are both small in the evolution process by introducing the best feasible solution,so the search efficiency and convergence speed are improved. Finally the modified mutation strategy is also used to better integrate the overall performance.
Without loss of generality,COPs can be defined as to:
| $\eqalign{ & \min f\left( X \right) \cr & {\rm{s}}{\rm{.t}}\left\{ \matrix{ {g_i}\left( X \right) \le 0,i = 1, \cdots ,p \hfill \cr {h_j}\left( X \right) = 0,j = 1, \cdots q \hfill \cr} \right. \cr} $ | (1) |
where X =(x1,…xn)∈Rn is the vector of solution; f(X) is the objective function that are required to be optimized; gi(X) is the ith inequality constraint and p is the number of inequality constraints; hi(X) is the jth equality constraint and q is the number of equality constraints. Each xi , i =1,2,…, n is bounded by lower and upper limits
Definition 1 (Constraint violation)
Constraint violation function is defined as Eq. (2)[17],whose size is called the constraint violation.
| $\begin{align} & G\left( X \right)=\sum\limits_{i=1}^{p}{\max \left( 0,{{g}_{i}}\left( X \right) \right)}+ \\ & \sum\limits_{j=1}^{q}{\max \left( 0,\left| {{h}_{j}}\left( X \right) \right|-\delta \right)} \\ \end{align}$ | (2) |
The studies have shown that differential evolution algorithm takes the advantages in keeping diversity and search capabilities compared with other evolutionary algorithms. This paper makes use of improved differential evolution algorithm to further strength the performance on COPs.
Like any other evolutionary algorithm,the initial population of DE is randomly generated according to a uniform distribution between the lower and upper limits ( li and ui ) defined for each component xi , i =1,2,…,n . After initialization,DE enters a loop of evolutionary operations: mutation,crossover and selection.
Mutation: At each generation t ,this operation creates mutation vectors Vi(t)based on the current parent population {Xi(t)| i =1,2,…, N }, N is the population size.
| ${{V}_{i}}\left( t \right)={{X}_{r1}}\left( t \right)+F\times \left( {{X}_{r2}}\left( t \right)-{{X}_{r3}}\left( t \right) \right)$ | (3) |
where indices r 1, r 2 and r 3 are distinct integers uniformly chosen from the set {1,2,…, N }; t is the generation of evolution; F is the mutation factor which ranges from 0 to 1.
Crossover: a binary crossover operation forms the following vector
| $\eqalign{ & {U_i}\left( t \right) = \left[ {{u_{i,1}}\left( t \right),{u_{i,2}}\left( t \right), \cdots ,{u_{i,n}}\left( t \right)} \right] \cr & {u_{ij}}\left( t \right) = \left\{ \matrix{ {v_{ij}}\left( t \right),{\rm{rand}}\left( j \right) \le CR \hfill \cr {x_{ij}}\left( t \right),{\rm{otherwise}} \hfill \cr} \right. \cr} $ | (4) |
where CR is crossover probability; rand( j ) is a random number between 0 and 1; vi,j(t) is the jth component of Vi(t); xi,j(t) is the jth component of Xi(t).
Selection: The selection operation selects the better one from the parent vector Xi(t) and the trial vector Ui(t) according to their objective function values f ( ).
| ${{X}_{i}}\left( t \right)=\left\{ \begin{align} & {{U}_{i}}\left( t \right),f\left( {{U}_{i}}\left( t \right) \right)<f\left( {{X}_{i}}\left( t \right) \right) \\ & {{X}_{i}}\left( t \right),f\left( {{U}_{i}}\left( t \right) \right)\ge f\left( {{X}_{i}}\left( t \right) \right) \\ \end{align} \right.$ | (5) |
Many constrained optimization algorithms are easy to fall into local optima and their convergence accuracy are weak when they handle COPs with some equality constraints and high dimension of decision variables. This is because that there is no good diversity in the evolution population. After extensive research,a constrained optimization algorithm with dual populations is introduced in this paper.
3.1 The Improved Double PopulationsThe feasible solutions and infeasible solutions are saved respectively by dual population mechanism. Generally the infeasible solutions with small constraint violation are reserved by the infeasible set in some current algorithms[14-16].However,these infeasible solutions with poor objective function value can be retained,which has an unfavorable impact on the convergence speed of population. Besides,separating the relationship completely between the feasible solution and the infeasible solution in these algorithms will result in no exchange of information among them in evolution process,so it can reduce the search efficiency and convergence speed.Thence,this paper develops a novel definition as shown in definition 2 to update infeasible solution set,so the individuals can be preserved whose objective function value and constraints violation are both good. This will not only ensure the fine diversity of population,but also take into account the convergence.
Definition 2 (Constraints domination)
Given two infeasible solutions X and Y ,if the following three conditions are satisfied:
1) f(X)≤ f(B)∧ f(Y)≤ f(B)
2) f(X)≤ f(Y)∧ G(X)≤ G(Y)
3) f(X)< f(Y)∨ G(X)< G(Y)
Then infeasible solution X is called to dominate infeasible solution Y. Where B is the feasible solution whose objective value f(B) is the smallest in the feasible solution set.
From the Definition 2 we can see that infeasible solutions are not inferior to feasible solution in the objective function value,so these infeasible solutions will guide population close to the better feasible direction. Especially when feasible domain boundary is close to the global optimal solution,letting infeasible solution whose objective function value and constraints violation are both good to participate in evolution process will promote production of the feasible solution with high quality. Or there are multiple isolated feasible regions on COPs,the participation of excellent infeasible solution can expand the range of the search space and strength the links among different feasible regions. Subsequently the diversity of the population is increased to avoid getting in local optimum.Meanwhile,infeasible solutions are linked with the best feasible solution in the evolution which promotes the exchange of information between them.
In summary,the infeasible set is updated as follows: the infeasible set of last generation and the infeasible set of current generation are combined into a new set,from which the best N 2 (the scale of infeasible set) infeasible solutions are selected to be the infeasible set of the next generation according to Definition 2. If the number of these infeasible solutions is greater than N 2,the N 2 solutions with the smallest degree of constraint violation will be selected to be the infeasible set of the next generation. Meanwhile,the update of feasible set is similar with the infeasible set: the feasible set of last generation and the feasible set of current generation are merged to a new set,then the best N 1 (the scale of feasible set) feasible solutions are selected as the next generation feasible set according to their objective function values.
The update of infeasible solution set exist a close relationship with feasible solution set. The participation of infeasible feasible solutions with smaller constraint violation in the evolution process will facilitate population close to the feasible region,and it is possible to expand the exploration range. Also these infeasible solution own smaller objective function value,which will speed up the convergence. Then the diversity of population is kept well and search efficiency is also heightened.
3.2 The Improved Mutation OperationThe mutation operation in differential evolution algorithm plays a very important role in evolutionary process,yet some existing mutation strategies are short of coordinating exploration and exploitation ability,which results in local optimum easily. This paper presents an advanced mutation to enhance the diversity of the population by allowing the infeasible solution to take part in mutation process.
| $\begin{align} & {{V}_{i}}={{X}_{r1}}+\text{rand}\times \left( {{X}_{pro}}-{{X}_{r2}} \right)+ \\ & \text{rand}\times \left( {{X}_{r3}}-{{X}_{r4}} \right) \\ \end{align}$ | (6) |
where rand is a random number between 0 and 1; Xpro is the best feasible solution in the feasible set with probability pr or the random selected infeasible solution in the infeasible solution set with probability 1-pr .Xr1, Xr2, Xr3 and Xr4 are random chosen feasible solutions from feasible solution set,and pr is set as shown in Eq. (7).
| $pr=\left\{ \begin{matrix} 0.5+0.4t/{{G}_{\max }}, & t\le 0.5{{G}_{\max }} \\ 1, & t>0.5{{G}_{\max }} \\ \end{matrix} \right.$ | (7) |
where t is the generation of evolution; Gmax is the maximum generation of evolution.
Eq. (6) consists of three parts: Xr1 represents basic vector which will enlarge search scope and improve diversity of population. rand×(Xpro-Xr2) is on behalf of the best guiding part which can increase the exploitation ability of the population and promote the exchange of information between the individuals and the best individual. rand×(Xr3-Xr4) stands for random difference vector which can generate random perturbations.
The value of pr in Eq. (7) becomes lager with the evolution generation increase. It is necessary to enlarge exploration range in the early evolution for enhancing diversity of the population,so some excellent infeasible solution are used to strength the exploration ability. But in order to guarantee to converge to the global optimal feasible solution in the late evolution,we just let feasible solutions to participate in evolution.
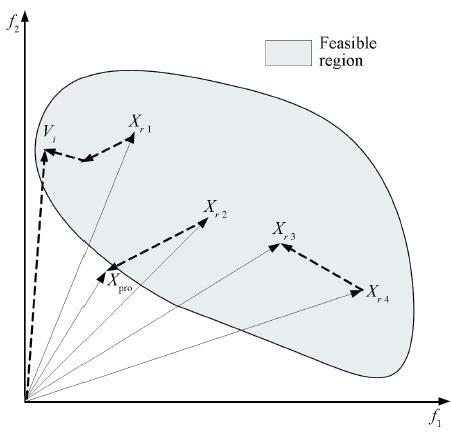
The following figures show that how the improved mutation operation influence production of new individuals. In Fig. 1,Xpro is the feasible solution with small objective function value,and the improved mutation operation will help individuals to approach the better objective value direction. Besides,Xpro is the infeasible solution in Fig. 2,and it can not only enhance diversity but also urge population to move towards the region with the better objective function value.

|
Figure 1 Xpro is feasible solution |
|
Figure 2 Xpro is infeasible solution |
4 Simulation Results
In order to validate the feasibility and efficiency of the proposed algorithm,it is compared with three advanced constrained optimization algorithms: ISR[11],εDE[18],εRDE[19]. We carry out an experiment on the standard test problems g01- g13[15]. The performance metrics are the best solution,the worst solution,mean and standard deviation[18]. The parameters in this paper are set as follows: the initial population size is set to 100 and the maximum generation of evolution is set to 10 000,and the feasible set scale is 100 and the infeasible set scale is 20. The above related parameters refer to Refs. [14] and [18]. Experiment results are shown in Table 1 for 30 independent runs.
As shown in Table 1,our algorithm is consistent to convergence to the global optimal solution on twelve functions for 30 independent runs except on g13. However,the ISR can only uniform convergence to the global optimal solution on nine functions except on g02, g07, g10, g13,εRDE is capable of reaching the global optimal solution unanimously on eleven function except on g02,g07,εDE is able to convergence to the optimal solution consistently on eleven function except on g02, g13. The proposed algorithm is almost superior to ISR on all test functions and ISR is not fully consistent to convergence on g02, g07, g10. It shows that the defect of diversity maintenance results in ISR's incomplete convergence. Thus the suggested algorithm has better performance than ISR in keeping the diversity of population. When comparing with εRDE and εDE on g02,the presented algorithm convergence completely to the global optimal solution for 30 independent runs. This shows that our algorithm has better optimization performance on g02 whose dimensionality of decision variables is high. This can imply that our algorithm is more suitable for solving those problems with wide search range like g02 which require good exploration ability of algorithms. On g07,the worst solution obtained by εRDE is inferior to our algorithm and εRDE does not always converge to the best solution. For the problems with complex equality constraints such as g13,whose feasible region is very small,our algorithm will fall into local optimum likes ISR and εDE. It shows that these three algorithms need to further improve diversity of population on dealing with the problems of some equality constraints.εRDE own the best performance among four algorithms,which indicates its optimal performance of diversity maintenance on g13.
| Table 1 The comparison of three algorithms |
Besides,the standard deviation of the proposed algorithm is generally smaller which indicates that the robustness of our algorithm is better than other three excellent algorithms. In short,the suggested algorithm has certain advantage in solving thirteen basic test functions.
5 ConclusionsA constrained optimization algorithm based on double populations is presented in this paper.The improved double populations can avoid direct comparison of the feasible solutions and the infeasible solutions and constraint domination is employed to update the infeasible set,so the effective information of the infeasible solution can be fully utilized and the diversity is enhanced.Then,we use the modified mutation operation to further raise the overall performance. Finally,simulation results on test problems g01- g13 show that the proposed algorithm has certain advantages than other algorithms because it can ensure good convergence and robustness.
But especially for these COPs with some equality constraints and high dimension of decision variable,it is still necessary for us to research with more energy.
| [1] |
Jain H, Deb K. An evolutionary many-objective optimization algorithm using reference-point based non-dominated sorting approach, part II: Handling constraints and extending to an adaptive approach.
IEEE Transactions on Evolutionary Computation,2014, 18 (4) : 602-622.
( 0) 0)
|
| [2] |
Bhandari A K, Singh V K, Kumar A, et al. Cuckoo search algorithm and wind driven optimization based study of satellite image segmentation for multilevel thresholding using Kapur’s entropy.
Expert Systems with Applications,2014, 41 (7) : 3538-3560.
( 0) 0)
|
| [3] |
Karaboga D, Gorkemli B, Ozturk C, et al. A comprehensive survey: artificial bee colony algorithm and applications.
Artificial Intelligence Review,2014, 42 (1) : 21-57.
( 0) 0)
|
| [4] |
Yeh W C, Chuang M C. Using multi-objective genetic algorithm for partner selection in green supply chain problems.
Expert Systems with Applications,2011, 38 (4) : 4244-4253.
( 0) 0)
|
| [5] |
Li X, Yao X. Cooperatively coevolving particle swarms for large scale optimization.
IEEE Transactions on Evolutionary Computation,2012, 16 (2) : 210-224.
( 0) 0)
|
| [6] |
Elsayed S M, Sarker R A, Essam D L. An improved self-adaptive differential evolution algorithm for optimization problems.
IEEE Transactions on Industrial Informatics,2013, 9 (1) : 89-99.
( 0) 0)
|
| [7] |
Shang R, Jiao L, Ren Y, et al. Quantum immune clonal co-evolutionary algorithm for dynamic multi-objective optimization.
Soft Computing,2014, 18 (4) : 743-756.
( 0) 0)
|
| [8] |
Mezura-Montes E, Coello Coello C A. Constraint-handling in nature-inspired numerical optimization: past, present and future.
Swarm and Evolutionary Computation,2011, 1 (4) : 173-194.
( 0) 0)
|
| [9] |
Rodrigues S, Bauer P, Bosman P A N.
A novel population-based multi-objective CMA-ES and the impact of different constraint handling techniques. Proceedings of the 2014 Conference on Genetic and evolutionary computation. Vancouver, Canada: ACM, 2014 : 991 -998.
( 0) 0)
|
| [10] |
Mallipeddi R, Suganthan P N. Ensemble of constraint handling techniques.
IEEE Transactions on Evolutionary Computation,2010, 14 (4) : 561-579.
( 0) 0)
|
| [11] |
Runarsson T P, Yao X. Search biases in constrained evolutionary optimization.
IEEE Transactions on Systems, Man, and Cybernetics,2005, 35 (2) : 233-243.
( 0) 0)
|
| [12] |
Deb K. An efficient constraint handling method for genetic algorithms.
Computer Methods in Applied Mechanics and Engineering,2000, 186 (2) : 311-338.
( 0) 0)
|
| [13] |
Takahama T, Sakai S.
Constrained optimization by the ε constrained differential evolution with an archive and gradient-based mutation. Proceedings of the 2010 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2010 : 1 -9.
( 0) 0)
|
| [14] |
Meng Hongyun, Zhang Xiaohua, Liu Sanyang. A differential evolution based on double population for constrained multi-objective optimization problems.
Chinese Journal of Computers,2008, 31 (2) : 229-235.
( 0) 0)
|
| [15] |
Bi Xiaojun, Wang Yanjiao. Constraint multi-objective evolutionary algorithm based on artificial bee colony algorithm.
Journal of Jilin University,2013 (2) : 397-403.
( 0) 0)
|
| [16] |
Zhang L F, He R, Yan M L.
Heterogeneous double populations based hybrid genetic algorithm design for training feedforward neural networks. Proceedings of the 2012 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2012 : 1 -8.
( 0) 0)
|
| [17] |
Wang Y, Cai Z. Combining multi-objective optimization with differential evolution to solve constrained optimization problems.
IEEE Transactions on Evolutionary Computation,2012, 16 (1) : 117-134.
( 0) 0)
|
| [18] |
Zheng Jianguo, Wang xiang, Liu Ronghui. ε-Differential evolution algorithm for constrained optimization problems.
Journal of Software,2012, 23 (9) : 2374-2387.
( 0) 0)
|
| [19] |
Takahama T,Sakai S.Efficient constrained optimization by the ε constrained rank-based differential evolution.WCCI 2012 IEEE world Congress on Computational Intelligence.Brisbane.http://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=6256111.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


