2. College of Mechanical Science and Engineering, Jilin University, Changchun 130022, China;
3. Department of Engineering, Saitama University, Saitama-ken , Japan
Spindle is a key unit of NC machine tools. The reliability of spindle plays an important role in reliability of NC machine tools, so how to evaluate spindle reliability of accurately is great significance[1]. Reliability evaluation of spindle is the basis of reliability design, test, operation and maintenance of NC machine tools.
It's well known that Weibull distribution is the most widely used in reliability studies such as software[2-3], machine tool[4-7], wind[8-10] and human[11-12]. The two-parameter Weibull distribution[6, 13-14], three-parameter Weibull distribution[15] and mixed Weibull distribution[16-17] are commonly used in reliability engineering.
Two-parameter and three-parameter Weibull distribution are only adapted to the single failure mode. In the case of failure modes are multiple for complex electromechanical system, mixed Weibull distribution is usually used. Different methods are used to estimate the parameters of mixed Weibull distribution. Maximum likelihood estimation (MLE) is widely used to estimate the parameters of mixed Weibull[18-20]. Tan[16] proposed a new approach to MLE of Weibull distribution with interval data. Mixed Weibull distributions was used for fitting failure times data by Razali[17], and Maximum likelihood estimation was used to estimate the parameters.
Xia[21] analyzed the reliability-based approach to bridge condition assessments with mixed Weibull distribution for finding the multi-modal peak stresses. Zhang[22] established a mixed Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data. Castet[23] provided an advanced parametric fit based on mixed Weibull distribution for nonparametric satellite reliability. From references, it will be found that most researchers used the MLE for parameters evaluation of mixed Weibull distribution. But MLE is more complex and may not exist, or it is difficult to get the final solution even if they exit.
The graphical method is another method for the estimation of mixed Weibull distribution[24-26]. It is introduced by Jiang et al.[24], and has been used extensively to estimate the parameters of mixed Weibull distribution. The method has been applied by Paulo[25] to analyze the wind speed. Although graphical method can get the estimated value, the subjectivity is very strong and the result is not accuracy.
Because the defect of parameters estimation with graphical method, we have proposed a new method to estimate the parameters of mixed Weibull. The method is combined the graphical method and genetic algorithm (GA). It can identify the failure data obeying mixed Weibull distribution with WPP, and then obtain the observed value of the parameters (shape and scale) with graphical method. The following can get the search interval of shape and scale parameters with loose coefficient, finally optimized the parameters with GA. The method for the estimation of parameters is quick and accurate.
2 Failure Model Identification 2.1 Failure Data CollectionFor evaluating the reliability level of spindle,42 spindles have been used in the reliability field test and 49 failures are collected. The time between failures is shown in Table 1.
| Table 1 Test sample failure data |
2.2 Weibull Probability Paper
The time between failures of spindle may obey several types of distribution, such as normal distribution, two or three parameter Weibull distribution and mixed Weibull distribution.To selecting the best distribution, Weibull probability paper (WPP) is drawn to identify which distribution is fit[24]. Weibull probability paper (WPP) is shown in Fig. 1.
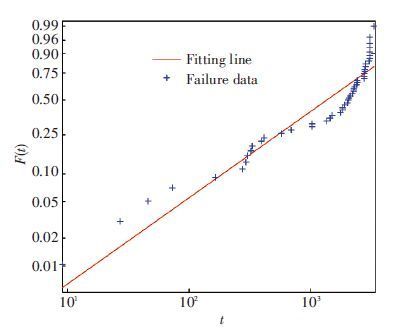
|
Figure 1 WPP of spindle |
If there is no obvious turning point on the WPP, presented in a straight line, two-parameter or three-parameter Weibull distribution is used to fit the data. If there is an obvious turning point on the WPP, the spindle will meet the three-parameter Weibull distribution or the mixed Weibull. As shown in Fig. 1, there is not a straight line and with an obvious turning point. So this paper proposes using mixed Weibull distribution for reliability modeling[27].
3 Reliability Modeling 3.1 Mixed Weibull ModelThe mixed Weibull model function is shown as follows[28]:
R(t)=pR1(t)+qR2(t)=
| $p\exp \left[{ - {{\left( {\frac{t}{{{a_1}}}} \right)}^{\beta 1}}} \right] + q\exp \left[{ - {{\left( {\frac{t}{{{a_2}}}} \right)}^{\beta 2}}} \right]$ | (1) |
where β1 and β2 are shape parameters; α1 and α2 are scale parameters; p and q are the proportion of the two-parameter Weibull distribution in mixed Weibull model.
For the spindle, there are two types of failure.One is sudden failure, it means failure by lost strength and the shape parameter β1<1, another is abrasion failure and the shape parameter β2>1[27]. If α1=α2 and β1=β2, the mixed Weibull has transformed the two-parameter Weibull.
3.2 Parameter EstimationBecause the problems of graphical method and maximum likelihood estimation, this paper proposes a method that combined graphical method and genetic algorithm(GA) for parameter estimation.
GA is a kind of adaptive and intelligent search technology with global optimization. The most successful applications are complex nonlinear optimization problem and it will find a satisfactory solution. The search interval of shape and scale for GA is got with graphical method. The steps of parameter estimation are shown as follows:
(1) Calculate xi and yi(i=1,2,…,n).
Let all the time between failures in Table 1 in ascending order, and record as ti,(i=1,2,…,n)[27-28]. So xi and yi are got with Eq.(2).
| $\left\{ \begin{align} & {{x}_{i}}=\ln \left( {{t}_{i}} \right) \\ & {{y}_{i}}=\ln \left[ -\ln \left( 1-\frac{i-0.3}{n+0.4} \right) \right] \\ \end{align} \right.$ | (2) |
(2) Plot asymptote in WPP.
Drawing (xi,yi),i=1,2,…,n, in the WPP, then searching two asymptote line y=ax+b as shown in Fig. 2. The asymptote record as L1,L2, and the expressions as follows:
| $\left\{ \begin{align} & {{L}_{1}}:y=0.799lx-5.9315 \\ & {{L}_{2}}:y=3.290lx-25.5467 \\ \end{align} \right.$ | (3) |
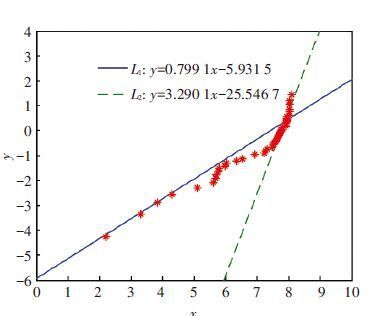
|
Figure 2 WPP and graph fitting of spindle |
(3) Define the search interval.
Through Eq.(3) to Eq.(9), it can obtain the observed value slope a^ and ordinate b^ via least square. Meanwhile, from Eq.(10) it can be got shape parameters β1,β2, and scale parameters α1,α2.
| $\left\{ \begin{align} & \hat{b}={{l}_{xy}}/{{l}_{xx}} \\ & \hat{a}=\bar{y}-{{{\hat{b}}}_{xx}} \\ \end{align} \right.$ | (4) |
| ${{l}_{xx}}=\sum\limits_{i=1}^{n}{{{\left( {{x}_{i}}-\overset{-}{\mathop{\text{ }x}}\, \right)}^{2}}}=\sum\limits_{i=1}^{n}{x}\overset{2}{\mathop{\text{ }i}}\,-n{{\overset{-}{\mathop{\text{ }x}}\,}^{2}}$ | (5) |
| ${{l}_{xx}}=\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-\overset{-}{\mathop{\text{ }y}}\, \right)}^{2}}}=\sum\limits_{i=1}^{n}{y}\overset{2}{\mathop{\text{ }i}}\,-n{{\overset{-}{\mathop{\text{ }y}}\,}^{2}}$ | (6) |
| ${l_{xx}} = \mathop \sum \limits_{i = 1}^n \left( {{x_i} - \mathop x\limits^ - } \right)\left( {{y_i} - \mathop y\limits^ - } \right) = \mathop \sum \limits_{i = 1}^n {x_i}{y_i} - n\mathop x\limits^ - \mathop y\limits^ - $ | (7) |
| $\mathop x\limits^ - = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {x_i}$ | (8) |
| $\mathop y\limits^ - = \frac{1}{n}\mathop \sum \limits_{i = 1}^n {y_i}$ | (9) |
| $\left\{ \begin{align} & \hat{\beta }=\hat{b} \\ & \hat{a}=\exp \left( -\hat{a}/\hat{b} \right) \\ \end{align} \right.$ | (10) |
According to the given loose coefficient k(0≤k≤1), and the expression of L1 and L2, we can obtained the four parameters observation through the least square α10=1 668,β10=0.779 2,α20=2 355 and β20=3.290 1. The search interval of each parameter is as follows:
| $\left\{ \begin{align} & {{a}_{1}}\in \left[ \left( 1-k \right)\bullet {{a}_{10}},\left( 1+k \right)\bullet {{a}_{10}} \right] \\ & {{\beta }_{1}}\in \left[ \left( 1-k \right)\bullet {{\beta }_{10}},\left( 1+k \right)\bullet {{\beta }_{10}} \right] \\ & {{a}_{2}}\in \left[ \left( 1-k \right)\bullet {{a}_{20}},\left( 1+k \right)\bullet {{a}_{20}} \right] \\ & {{\beta }_{2}}\in \left[ \left( 1-k \right)\bullet {{\beta }_{20}},\left( 1+k \right)\bullet {{\beta }_{20}} \right] \\ \end{align} \right.$ | (11) |
For expanding the scope of parameters' search interval from Eq.(11), we have chosen loose coefficient k=0.8. Because shape parameter β1<1 and β2>1, so the max value of β1 and the min value of β2 is 1 . The interval of parameters is shown in Table 2.
| Table 2 Parameters observations and search interval |
(4) Parameters optimization.
Fitness function is the key of genetic algorithm. It has important influence on the speed of convergence and reconciliation precision. Because spindle failure data has the feature of small sample, so we extend d test as a fitness function.
Let all the failure data in ascending order, then computing the difference of hypothesis distribution (mixed Weibull distribution) function F0(ti) and the empirical distribution function Fn(ti). The smaller of the difference, the better of it fits the hypothesis distribution. The largest value of the difference's absolute is regarded as test statistics Dn. Its expression is shown as follows:
| ${D_n} = \mathop {\sup }\limits_{ - \infty < x < + \infty } |{F_n}\left( {{t_i}} \right) - {F_0}\left( {{t_i}} \right)| = \max \left\{ {{d_i}} \right\} < {D_n}{,_a}$ | (12) |
where F0(ti) is mixed Weibull distribution function; Fn(ti) is empirical distribution function and the expression as shown in Eq.(13); di is distribution of deviation as shown in Eq.(14); Dn,α is critical value and the expression as shown in Eq.(15) when confidence level α=0.1.
| ${{F}_{n}}\left( {{t}_{i}} \right)=\left\{ \begin{align} & 0, t<{{t}_{i}} \\ & \frac{i-0.3}{n+{{0.4}^{,}}}{{t}_{i}}<t<{{t}_{i}}_{+1} \\ & 1, t\ge {{t}_{n}} \\ \end{align} \right.$ | (13) |
| ${d_i}| = |{F_n}\left( {{t_i}} \right) - {F_0}\left( {{t_i}} \right)|$ | (14) |
| ${D_n}{,_a} = \frac{{1.22}}{{\sqrt n }}$ | (15) |
The test statistic Dn and the critical value Dn,α are analyzed. If the critical value is greater than the test statistics, the hypothesis is accepted, otherwise rejected. So the fitness is shown as follows:(x)=Dn-Dn,a=
| $\max \left\{ {|\mathop {{F_n}}\limits^{n, a} \left( {{x_i}} \right)|} \right\} - {D_{n, a}}$ | (16) |
Fitness function value is much smaller, which indicates that the hypothesis distribution is close to the empirical distribution, it means the hypothesis distribution is more accurate. At the same time, if Fitness(x)<0, we can consider that the parameters have passed d test, and got the parameters estimation. We can get the parameters estimation and the fitness with Matlab. There are three kinds of operation in GA. Selection-reproduction, crossover as well as mutation. In the process of GA, the initial population is 200, and the generation gap is 0.9, and the crossover rate is 0.7, and the mutation rate is 0.01. After 500 iterations, the parameter estimates are obtained.
Because fitness is less than zero, so the estimated value of parameters is effective, and the time between failure obey mixed Weibull distribution. The estimated value is shown in Table 3. The reliability model graphic-GA is shown in Eq.(17). Eqs.(18)-(20) are the functions of graphical method, piecewise Weibull and two-Weibull.
| $R\left( t \right) = 0.3254 \times \exp - \left[{{{\left( {\frac{t}{{361}}} \right)}^{0.8676}}} \right] + 0.6746 \times \exp \left[{{{\left( {\frac{t}{{2712}}} \right)}^{3.4895}}} \right]$ | (17) |
| ${R_1}\left( t \right) = 0.5814 \times \exp - \left[{{{\left( {\frac{t}{{1668}}} \right)}^{0.7992}}} \right] + 0.4186 \times \exp \left[{{{\left( {\frac{t}{{2355}}} \right)}^{3.2901}}} \right]$ | (18) |
| ${{R}_{2}}\left( t \right)=\left\{ \begin{align} & \exp \left[ {{\left( \frac{t}{5422} \right)}^{0.6681}} \right],0\le t\le 940 \\ & 0.786\times \exp \left[ {{\left( \frac{t}{2311} \right)}^{29547}} \right],940<t \\ \end{align} \right.$ | (19) |
| ${R_3}\left( t \right) = \exp \left[{{{\left( {\frac{t}{{2126}}} \right)}^{0.8359}}} \right]$ | (20) |
| Table 3 Parameters estimated and fitness |
3.3 Model Optimization 3.3.1 Average cumulative error test
The average cumulative error is the average of absolute value of difference between empirical distribution function and hypothesis distribution function. The smallest of the average cumulative error of the fitting function is the best fitting function. The average cumulative error is usually calculated with Eq.(21).
| $\delta = \frac{1}{n}\mathop \sum \limits_{i = 1}^n |\mathop R\limits^ \wedge \left( {{t_i}} \right) - R\left( {{t_i}} \right)|$ | (21) |
Where R^(ti) is reliability function of empirical distribution function; R(ti) is reliability function of hypothesis distribution function.
3.3.2 Mean square error testMean square error (MSE) test refers to the mean value of the square root of the error of each measurement error. The smaller of MSE, the better of data fitting. MSE usually calculate with Eq.(22).
| $\varepsilon = \frac{1}{n}\sqrt {\mathop \sum \limits_{i = 1}^n \left[{\mathop R\limits^ \wedge \left( {{t_i}} \right) - R\left( {{t_i}} \right)} \right]} $ | (22) |
The four reliability model has been optimized by d test, the average cumulative error test and MSE respectively. All the tests indicate that the mixed Weibull distribution is best. The test value is shown in Table 4.
Fig. 3 shows reliability function curve of spindle with different methods. From Fig. 3, the function with graphical-GA is the best to fit the scatter diagram. The spindle failure includes sudden failure and abrasion failure. The first sub section describes the sudden failure, which reflectes that the spindle is on early failure period. Because all the spindles are minted, it does not running-in well. The second sub section describes that the spindle is on abrasion failure period. After a period of use, the early malfunction has been eliminated.
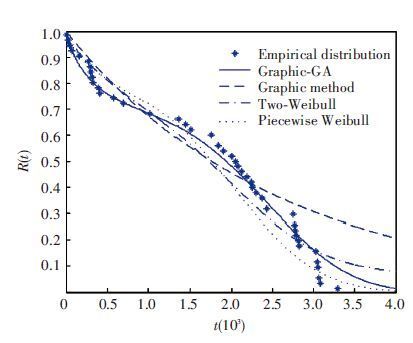
|
Figure 3 Reliability function curve |
| Table 4 Preferred test table |
4 Reliability Evaluation 4.1 MTBF Point Estimation
MTBF(Mean Time between Failure) point estimation is shown as follows:
| $MTBF = p \bullet {a_1} \bullet \Gamma \left( {1 + \frac{1}{{{\beta _1}}}} \right) + q \bullet {a_2}\Gamma \left( {1 + \frac{1}{{{\beta _2}}}} \right)$ | (23) |
So MTBF of spindle can calculate with Eq.(21).
| $MTBF = p \bullet {a_1} \bullet \Gamma \left( {1 + \frac{1}{{{\beta _1}}}} \right) + q \bullet {a_2}\Gamma \left( {1 + \frac{1}{{{\beta _2}}}} \right) = 1744\left( h \right)$ |
The hypothesis that θ* is estimate value of the unknown parameter θ. P is the probability of θ less than positive number δ, which is shown in Eq.(24).
| $P|\theta * - \theta | < \delta = 1 - a$ | (24) |
where α is significance level; 1-α is probability of θ in (θ*-δ,θ*+δ), and (θ-δ,θ*+δ) is confidence interval.
The reliability of spindle is time terminated testing, and confidence interval 1-α is 90%. It will get quantiles $x\frac{{^2a}}{2}$ and $x{}_1^2{ - _{\frac{a}{2}}}$ as follows:
| $p\left[{x\frac{{{{^2}_a}}}{2}\left( {2r} \right) \leqslant \frac{{2T*}}{\theta } \leqslant x\mathop 1\limits^2 - \frac{a}{2}\left( {2r + 2} \right)} \right] = 1 - a$ | (25) |
Hence Eq.(25) can be re-written as
| $p\left[{\frac{{2T*}}{{x\mathop 2\limits^1 - \frac{a}{2}\left( {2r + 2} \right)}} \leqslant \theta \leqslant \frac{{2T*}}{{x\frac{{{{^2}_a}}}{2}\left( {2r} \right)}}} \right] = 1 - a$ | (26) |
The two-sided confidence interval of MTBF can be intended as follows:
| $\frac{{2T*}}{{{x^2}\mathop {_{0.95}\left( {2r + 2} \right)}\limits^{} }} \leqslant \theta \leqslant \frac{{2T*}}{{{x^2}_{0.05}\left( {2r} \right)}}$ | (27) |
where r is failure number, and T is total testing time. Hence the two-sided confidence interval of spindle MTBF is (1 387.1,2 264.5), calculated with Eq.(27).
| $\eqalign{ & {\theta _{\min }} = \frac{{2T*}}{{{x^2}\mathop {_{0.95}\left( {2r + 2} \right)}\limits^{} }} = \frac{{2 \times 86236}}{{{x^2}\mathop {_{0.95}\left( {2 \times 49 + 2} \right)}\limits^{} }} = \cr & {\theta _{\min }} = \frac{{2T*}}{{{x^2}\mathop {_{0.05}\left( {2r + 2} \right)}\limits^{} }} = \frac{{2 \times 86236}}{{{x^2}\mathop {_{0.05}\left( {2 \times 49} \right)}\limits^{} }} = 2264\left( h \right) \cr} $ |
In this paper, a new method has introduced to evaluating reliability of spindle. From the preceding analysis, the conclusions can be drawn as follows:
1) According to time terminated reliability testing of spindle in manufacture, failure data were collected, then making model identification through WPP. The WPP has the obvious turning point, so the data of spindle may be obey mixed Weibull distribution.
2) In view of graphical method with less precision and the complexity in calculating of MLE, it has combined graphical method with genetic algorithm for parameters estimation, and processed d test as a fitness function. With the comparative analysis, it can verify that graphical-GA methods has the estimation more objective and higher precision.
3) MTBF point estimation and interval estimation of spindle with mixed Weibull distributionis evaluated. The result can provide the basis for design and reliability growth of spindle.
| [1] |
Bucar T, Nagode M, Fajdiga M. Reliability approximation using finite Weibull mixture distributions. Reliability Engineering and System Safety, 2004, 84(3): 241-251. ( 0) 0)
|
| [2] |
Febrero F, Calero C, Moraga M Á. A systematic mapping study of software reliability modeling. Information and Software Technology, 2014, 56(8): 839-849. ( 0) 0)
|
| [3] |
Pachauri B, Kumar A, Dhar J. Software reliability growth modeling with dynamic faults and release time optimization using GA and MAUT. Applied Mathematics and Computation, 2014, 242(9): 500-509. ( 0) 0)
|
| [4] |
Wang Yiqiang, Shen Guixiang, Jia Yazhou. Multidimensional force spectra of CNC machine tools and their applications, part two: reliability design of elements. International Journal of Fatigue, 2003, 25(5): 447-452. ( 0) 0)
|
| [5] |
Jia Yazhou, Jia Zhixin. Fatigue load and reliability design of machine-tool components. International Journal of Fatigue, 1993, 15(1): 47-52. ( 0) 0)
|
| [6] |
Wang Zhiming, Yang Jianguo. Numerical method for Weibull generalized renewal process and its applications in reliability analysis of NC machine tools. Computers & Industrial Engineering, 2012, 63(4): 1128-1134. ( 0) 0)
|
| [7] |
Kono D, Lorenzer T, Weikert S, et al. Evaluation of modelling approaches for machine tool design. Precision Engineering, 2010, 34(3): 399-407. ( 0) 0)
|
| [8] |
Touré S. Investigations on the Eigen-coordinates method for the 2-parameter weibull distribution of wind speed. Renewable Energy, 2005, 30(4): 511-521. ( 0) 0)
|
| [9] |
Lun I Y F, Lam J C. A study of Weibull parameters using long-term wind observations. Renewable Energy, 2000, 20(2): 145-153. ( 0) 0)
|
| [10] |
Akdag S A, Dinler A. A new method to estimate Weibull parameters for wind energy applications. Energy Conversion and Management, 2009, 50(7): 1761-1766. ( 0) 0)
|
| [11] |
Kim I S. Human reliability analysis in the man-machine interface design review. Annals of Nuclear Energy, 2001, 28(11): 1069-1081. ( 0) 0)
|
| [12] |
Mosleh A, Changa Y H. Model-based human reliability analysis: prospects and requirements. Reliability Engineering & System Safety, 2004, 83(2): 241-253. ( 0) 0)
|
| [13] |
Almalki S J, Nadarajah S. Modifications of the Weibull distribution: A review. Reliability Engineering and System Safety, 2014, 124: 32-55. ( 0) 0)
|
| [14] |
Elmahdy E E, Aboutahoun A W. A new approach for parameter estimation of finite Weibull mixture distributions for reliability modeling. Applied Mathematical Modelling, 2013, 37(4): 1800-1810. ( 0) 0)
|
| [15] |
Nagatsuka H, Kamakura T, Balakrishnan N. A consistent method of estimation for the three-parameter Weibull distribution. Computational Statistics & Data Analysis, 2013, 58: 210-226. ( 0) 0)
|
| [16] |
Tan Zhibin. A new approach to MLE of Weibull distribution with interval data. Reliability Engineering & System Safety, 2009. ( 0) 0)
|
| [17] |
Razali A M, Al-Wakeel A A. Mixture Weibull distributions for fitting failure times data. Applied Mathematics and Computation, 2013, 219: 11358-11364. ( 0) 0)
|
| [18] |
Akdag S A, Bagiorgas H S, Mihalakakou G. Use of two-component Weibull mixtures in the analysis of wind speed in the Eastern Mediterranean. Applied Energy, 2010, 87(8): 2566-2573. ( 0) 0)
|
| [19] |
Franco M, Vivo J M, Balakrishnan N. Reliability properties of generalized mixtures of Weibull distributions with a common shape parameter. Journal of Statistical Planning and Inference, 2011, 141(8): 2600-2613. ( 0) 0)
|
| [20] |
Martinez E Z, Achcar J A, Jácome A A A, et al. Mixture and non-mixture cure fraction models based on the generalized modified Weibull distribution with an application to gastric cancer data. Computer Methods and Programs in Biomedicine, 2013, 112(3): 343-355. ( 0) 0)
|
| [21] |
Xia H W, Ni Y Q, Wong K Y, et al. Reliability-based condition assessment of in-service bridges using mixture distribution models. Computers & Structures, 2012, 106. ( 0) 0)
|
| [22] |
Zhang Qing, Hua Cheng, Xua Guanghua. A mixture Weibull proportional hazard model for mechanical system failure prediction utilising lifetime and monitoring data. Mechanical Systems and Signal Processing, 2014, 43(1/2): 103-112. ( 0) 0)
|
| [23] |
Castet Jean-Francois, Saleh J H. Single versus mixture Weibull distributions for nonparametric satellite reliability. Reliability Engineering & System Safety, 2010, 95(3): 295-300. ( 0) 0)
|
| [24] |
Jiang R Y, Murthy D N P. Modeling failure-data by mixture of 2 Weibull distribution: a graphical approach. IEEE Trans Reliability, 1995, 44(3): 477-488. ( 0) 0)
|
| [25] |
Rocha Po A C, de Sousa R C, de Andrade C F, et al. Comparison of seven numerical methods for determining Weibull parameters for wind energy generation in the northeast region of Brazil. Applied Energy, 2012, 89(1): 395-400. ( 0) 0)
|
| [26] |
Barabadi A. Reliability model selection and validation using Weibull probability plot-A case study. Electric Power Systems Research, 2013, 101: 96-101. ( 0) 0)
|
| [27] |
Jiang Renyan. Weibull Model of National Characteristics, Parameter Estimation and Application. Beijing:Science Press, 1998, 34: 40-70. ( 0) 0)
|
| [28] |
Cran G W. Graphical estimation methods for Weibull distributions. Microelectronics Reliability, 1976, 15(1): 47-52. ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


