Since the large caliber high speed Davis gun was created, it provides a new effective tool in loading of large size articles, analyzing of penetration kinetics and other modern weapon [1-5]. But there is a problem that the long charge, long flame spreading distance along axis, and large mass of powders, means that the combustion situation and pressure distribution in the charge are more complex. Thus, how to guarantee the safety and stability of the launching process is an important thing. In view of the propellant, the long tubular powder[6] is better seen from its permeability and fleetly flame propagation speed. It can be useful to reduce the pressure wave when applying to the high speed Davis guns with large loading density. Besides, we need to establish a numerical model and master the interior ballistic rules in the large caliber high speed Davis gun.
In general, the normal two-phase flow method is widely applied in the modern interior ballistics [7-9] , which considering both the gas phase and the solid phase as continuous medium. But for tubular powder in the Davis gun, this kind of approach cannot be consistent with the actual situation. The length of the tubular powder is even longer than most of the bore diameter. No matter from size or morphology structure or other respects, the pseudo-fluid assumptions will surely take lots of errors[10]. Zhang [11] and Yuan [12] have mentioned about a new particle trajectory model, in which the gas field is described by Eulerian system, and the propellant particles are described by Lagrangian approach. And all the propellant particles at different initial position are trailed. So, in this paper we will try to establish a new model in a 480 mm high speed Davis gun by treating the tubular powders as discontinuous discrete groups. We will solve gas filed with Eulerian system and solid field with Lagrangian system. We call this model one-dimensional discrete group gas-solid two phase flow model. Numerical simulation results of this model would also provide a basis for the development of guns with such special structure characteristics.
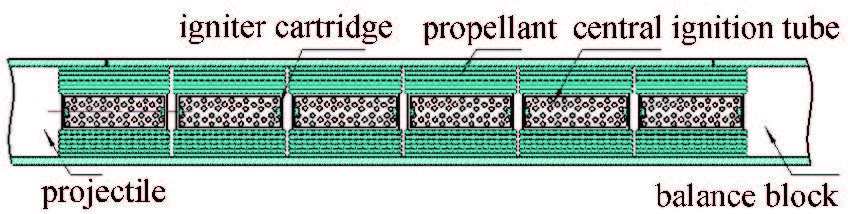
2 Structure System of the Davis GunFig. 1 shows the structure schematic diagram of the Davis gun system. The Davis gun system is composed of barrel gun carrier, balance block, propellant, ignition system, projectile, shear pin and so on. It uses the reverse motion of the balance block to offset the recoil force, which makes force balanced in the axial direction of the barrel[13-14]. In view of the long flame spreading distance, a center multi-point ignition system is designed as the ignition system[15-16].The double aromatic hydrocarbons 38/1 tubular powder is used as the propellant, which is known for its permeability, stability, and fast flame propagation speed. The tubular powder beams are divided into 9 equal pieces to compose 9 modules. There is one igniter cartridge in the center of each module. As a matter of convenience, we mark these propellant modules number 1-9 from the balance block side to the projectile side. The arrangement schematic diagram and real photo of the charge are shown in Figs. 2 and 3.

|
Figure 1 Schematic diagram of the Davis gun structure |
|
Figure 2 Schematic diagram of the charge arrangement |

|
Figure 3 Photo of the charge arrangement of the Davis gun |
The working process of Davis gun system is as follows: while ignition happens, black powders in the ignition powder bag (the snaking powder bag) are burned through the flame. Soon the interior ignition tube is split up with high temperature and high pressure. Energy would transfer through the igniter hole to the surface of the tubular powder beams. Thus the propellant burns. The sooner the propellant burns, the higher the pressure increases in the charge. If pressure on the base of the projectile or the balance block is high enough to get them unlocked, the projectile or the balance block will start to move. The whole interior ballistic process lasts until both of them are out of the muzzle.
3 Mathematical Model and Numerical Calculation MethodIn order to simulate the launching process described above, establishment of mathematical model is the first step to be taken into account.About the center igniter, we shall use the classical interior ballistic model in Ref. [17] to deal with. In this section we mainly describe the mathematical and numerical equations that constitute the one-dimensional discrete group gas-solid two-phase flow model in the charge.It can be divided into three parts to describe:the gas flow field equations and the motion equations of the tubular powder modules and some auxiliary equations.
3.1 Gas Flow EquationsIn this study, gas flow and motion of the propellant are simplified in one-dimension. And the turbulent viscosity and diffusion effect is neglected. Thus based on the assumption of an Eularian unsteady flow field perfect gases, the gas flow in the bore can be defined by a set of differential equations[18]: one mass conservation equation, one momentum conservation equation and one energy conservation equation, written as follows.
| $\begin{array}{*{20}{c}} {\frac{{\partial \left( {\phi {{\hat \rho }_{\rm{g}}}} \right)}}{{\partial t}} + \frac{{\partial \left( {\phi {{\hat \rho }_{\rm{g}}}{u_{\rm{g}}}} \right)}}{{\partial x}} = {{\dot m}_{\rm{c}}} + {{\dot m}_{{\rm{ig}}}}}\\ {\frac{\partial }{{\partial t}}\left( {\phi {{\hat \rho }_{\rm{g}}}{u_{\rm{g}}}} \right) + \frac{\partial }{{\partial x}}\left( {\phi {{\hat \rho }_{\rm{g}}}u_{\rm{g}}^2} \right) + \phi \frac{{\partial p}}{{\partial x}} = - {f_{\rm{s}}} + {{\dot m}_{\rm{c}}}{u_{\rm{p}}} + {{\dot m}_{{\rm{ig}}}}{u_{{\rm{ig}}}}}\\ {\frac{\partial }{{\partial t}}\left[ {\phi {{\hat \rho }_{\rm{g}}}\left( {{e_{\rm{g}}} + \frac{{u_{\rm{g}}^2}}{2}} \right)} \right] + \frac{\partial }{{\partial x}}\left[ {\phi {{\hat \rho }_{\rm{g}}}{u_{\rm{g}}}\left( {{e_{\rm{g}}} + \frac{p}{{{{\hat \rho }_{\rm{g}}}}} + \frac{{u_{\rm{g}}^2}}{2}} \right)} \right] + p\frac{{\partial \phi }}{{\partial t}} = }\\ { - {Q_{\rm{p}}} + {f_{\rm{s}}}{{\rm{u}}_{\rm{p}}} + {{\dot m}_{\rm{c}}}\left( {{E_{\rm{p}}} + \frac{p}{{{{\hat \rho }_{\rm{p}}}}} + \frac{{u_{\rm{p}}^2}}{2}} \right) + {{\dot m}_{{\rm{ig}}}}\left( {{e_{{\rm{ig}}}} + \frac{p}{{{{\hat \rho }_{{\rm{ig}}}}}} + \frac{{u_{{\rm{ig}}}^2}}{2}} \right)} \end{array}$ |
Where φ is the gas voidage; p is the pressure; ${\hat \rho }$ , e, u are the density, specific internal energy and the velocity, with the subscript g means the propellant gas, subscript c means the generated propellant gas, subscript ig means the propellant gas transferred from the igniter, and subscript p means the charge module; ${{{\dot m}_{\rm{c}}}}$ is the mass generation rate of propellant gas; ${{{\dot m}_{{\rm{ig}}}}}$ is the mass transmission rate of propellant gas from the igniter; fs is the resistance between the two phases; ${Q_{\rm{p}}} = {{\hat \rho }_{\rm{p}}}\left( {1 - \phi } \right){S_{\rm{p}}}q/{M_{\rm{p}}}$ is the heat transfer between the two phases; q is the heat conduction between the two phases; Sp , Mp are burning surface area and the initial mass of charge module.
3.2 Tubular Powder Motion EquationsThe tubular powder beams are divided into several modules based on their initial positions. We assume that they all move along the axial and simplify them with no collision or interference. Besides, the shape, size and attribute of each tubular powder beam are assumed to be the same, as also as combustion rules and movement rules. Thus, we established the motion model of the tubular powder modules based on the Lagrangian method, using the variable mass, momentum conservation equations, as follows:
| $\begin{array}{*{20}{c}} {\frac{{\rm{d}}}{{{\rm{d}}t}}\int_{{x_1}}^{{x_r}} {\left( {1 - \phi } \right){{\hat \rho }_{\rm{p}}}} {u_{\rm{p}}}A{\rm{d}}x = - \int_{{x_1}}^{{x_r}} {\left( {1 - \phi } \right)A{\rm{d}}p - } }\\ {\int_{{x_1}}^{{x_r}} {{{\dot m}_{\rm{c}}}{u_{\rm{p}}}A{\rm{d}}x} + \int_{{x_1}}^{{x_r}} {{f_{\rm{s}}}{\rm{d}}x} }\\ {\frac{{{\rm{d}}x}}{{{\rm{d}}t}} = {u_{\rm{p}}}} \end{array}$ |
where x is the displacement of the charge module; A is the cell sectional area.
3.3 Some Auxiliary Equations 3.3.1 Gas state equationThe Noble-Able state equation is always used in the interior ballistics:
| ${e_{\rm{g}}} = \frac{p}{{{{\hat \rho }_{\rm{g}}}\left( {k - 1} \right)}}\left( {1 - \alpha {{\hat \rho }_{\rm{g}}}} \right)$ |
where k is the specific heat ratio.
3.3.2 The friction resistance coefficient equationThe friction resistance coefficient equation was recommended in Ref. [19] as follows:
| $\begin{array}{ccccc} {C_{\rm{f}}} = & \left\{ {\begin{array}{*{20}{l}} {0.17, }&{\phi \le 0.6}\\ {0.17 - 0.152\left( {\phi - 0.6} \right)/0.2, }&{0.6 < \phi \le 0.8}\\ {0.018, }&{0.8 < \phi \le 1.0} \end{array}} \right.\\ {C_{\rm{f}}} = \frac{{{f_{\rm{s}}}}}{{\left[ {\left( {1 - \phi } \right)/{d_p}} \right]\left| {{u_{\rm{g}}} - {u_{\rm{p}}}} \right|\left( {{u_{\rm{g}}} - {u_{\rm{p}}}} \right){{\hat \rho }_{\rm{g}}}}} \end{array}$ |
where Cf is the frictional resistance coefficient; dp is the equivalent diameter of the tubular powder.
3.3.3 The heat transfer equationThe heat transfer is composed of radiation heat transfer and convection heat transfer, as follows:
| $q = {q_c} - {q_r}$ |
According to the Stefan-Boltzmann rules, the radiation heat transfer can be written as
| ${q_r} = {\varepsilon _{\rm{p}}}\sigma \left( {T_{\rm{g}}^4 - T_{{\rm{ps}}}^4} \right)$ |
where εP the particle surface gray degree; σ is the Stefan-Boltzmann constant; Tg is the gas temperature; Tps is the powder surface temperature.
The convection heat transfer is shown as follows:
| ${q_c} = h\left( {{T_{\rm{g}}} - {T_{{\rm{ps}}}}} \right)$ |
where h is the convection heat transfer coefficient.
3.3.4 The powder surface temperature equationAbout the powder surface temperature equation, we will use the equation acquired in Ref. [14], which can be rewritten as follows:
| ${T_{{\rm{ps}}}} = {T_{{\rm{pso}}}} + \frac{{2q}}{{{\lambda _{\rm{p}}}}}\sqrt {\frac{{{a_1}}}{\pi }} \left[ {{{\left( {t + \Delta t} \right)}^{1/2}} - {t^{1/2}}} \right]$ |
where Tpso is the initial temperature on the powder surface; a1 is the temperature diffusivity;λp is the particle thermal conductivity;
3.3.5 The burning rate modelThe burning rate model is based on the classical assumption that all the chemical reactions are very fast and occur in an ideal thin layer, at the surface of the solid propellant. Therefore, the overall macroscopic result of these phenomena is a regression rate of the propellant grain that can be represented by the so-called burning rate. In this study, we shall use the average value to calculate the burning rate by ignoring the temperature difference on the surface of each beam. Thus, the burning rate can be described as follows.
| $\begin{array}{*{20}{c}} {\dot r = b{p^n};\frac{{{\rm{d}}{r_{\rm{i}}}}}{{{\rm{d}}t}} = \dot r;\frac{{{\rm{d}}{r_{\rm{c}}}}}{{{\rm{d}}t}} = - \dot r}\\ {{m_{\rm{c}}} = {\rho _{\rm{p}}}\bar A\dot r;\bar A = \frac{{{\rho _{\rm{p}}}{\phi _{\rm{p}}}S}}{{{M_{\rm{p}}}}}} \end{array}$ |
where b, n are the burning rate coefficient and burning rate index; ri is the inner hole radius; rc is the outer hole radius;S=σSp; Mp=Mp1(1-ψ);S is the combustion area;Mp1 is the initial mass of the propellant; ψ is the propellant burned fraction.
3.3.6 The dynamics equation of the projectile and the balance blockThe dynamics equations of the projectile and the balance block are as follows:
| $\frac{{{\rm{d}}{v_{\rm{1}}}}}{{{\rm{d}}t}} = \frac{{{p_{{\rm{d1}}}}{A_1}}}{{{m_1}{\varphi _1}}}, \frac{{{\rm{d}}{v_{\rm{2}}}}}{{{\rm{d}}t}} = \frac{{{p_{{\rm{d2}}}}{A_2}}}{{{m_2}{\varphi _2}}}$ |
where pd1, pd2 are the pressure on the base of the projectile and the balance block;A1, A2 are the cross-sectional area on the base of the projectile and the balance block;v1, v2 are the velocity of the projectile and the balance block;φ1, φ2 are the secondary power coefficient.
3.4 Numerical Calculation MethodThe Euler-Lagrange mixed equations of the interior ballistic are usually solved with PSIC method proposed by Crowe. The basic idea is to constitute differential equations by integrating the gas flow model in Eulerian coordinate system, according to the unit control volume method. In addition, to acquire the trajectories, size and speed of the tubular modules, the discrete groups motion model are integrated in the gas grid cells, which considering changes of mass, momentum and energy in Lagrangian coordinate system. At the same time, the gas flow is also affected by the mass, momentum and energy changes of the discrete groups. By the way, the predictor corrector two steps MacCormack[18] scheme is used to solve the gas phase equations.
On the other hand, boundary conditions are also very important for a correct simulation of the gas flow and the solid behavior. Several types of boundary conditions are used in this study. Firstly, walls[18] are applied to the base of the projectile and the balance block. When the projectile or the balance block is still static, the walls boundary is stationary. Otherwise, the walls will move as them. And the tubular powder-wall collision is characterized to be perfect elastic collision, which means after collision, the powder beams are assumed the same velocity with no change in its energy. Secondly, the outflow boundary[20] is used to deal with the situation when the projectile or the balance block goes out of the calculation domain. Those tubular modules leaving the calculation space through this boundary are not included into further calculations.
4 Results and DiscussionsThe numerical simulation is on the background of a certain 480 mm Davis gun project .Two shot tests were already conducted to verify the codes. One set of parameters is as follows: the mass of the projectile is 1.31 t; the mass of the balance block is 7 t; the mass of the propellant in the charge is 369 kg, which is composed of 9 Modules. Another set of parameters is as follows: the mass of the projectile is 1.5 t; the mass of the balance block is 7 t; the mass of the propellant in the charge is 387 kg, which is composed of 9 Modules. The test system is made up of several parts: the high-speed video system, the net target, the multi-channel recording machine, the chamber pressure sensors and so on. The high-speed video system is used to get the projectile velocity in the muzzle. The net target is used to measure velocity of the projectile. The pressure sensors are placed at 1# pressure point which nears the initial charge, 2# pressure point which is at the side of the projectile, and the last one -3# pressure point which is close to the muzzle.
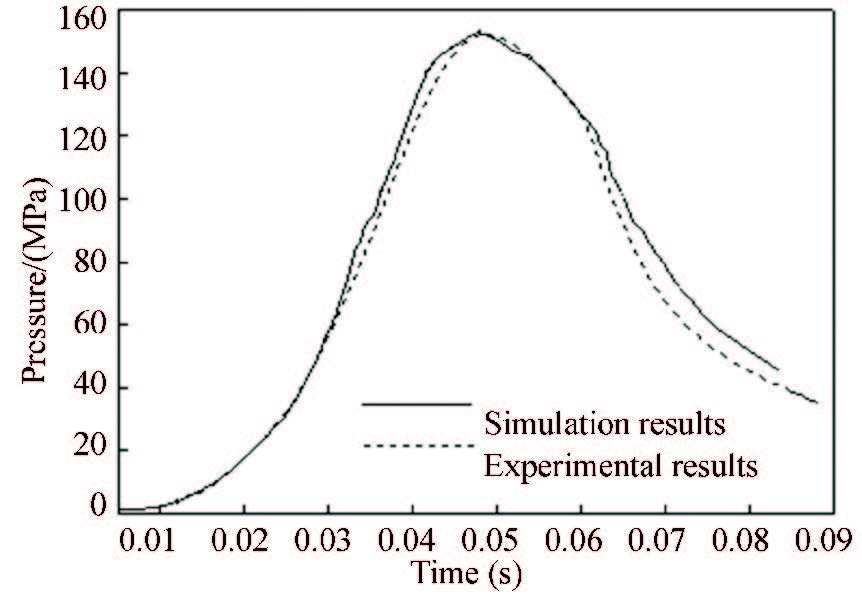
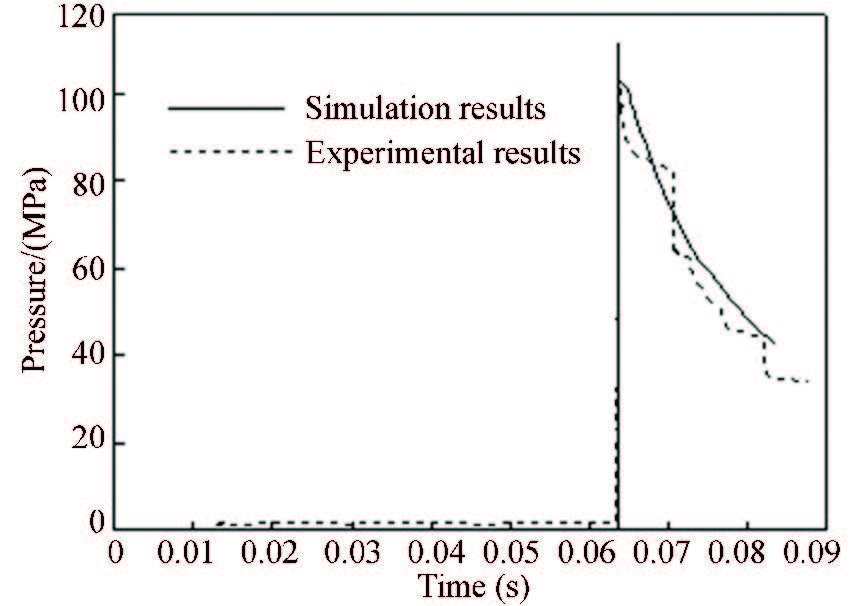
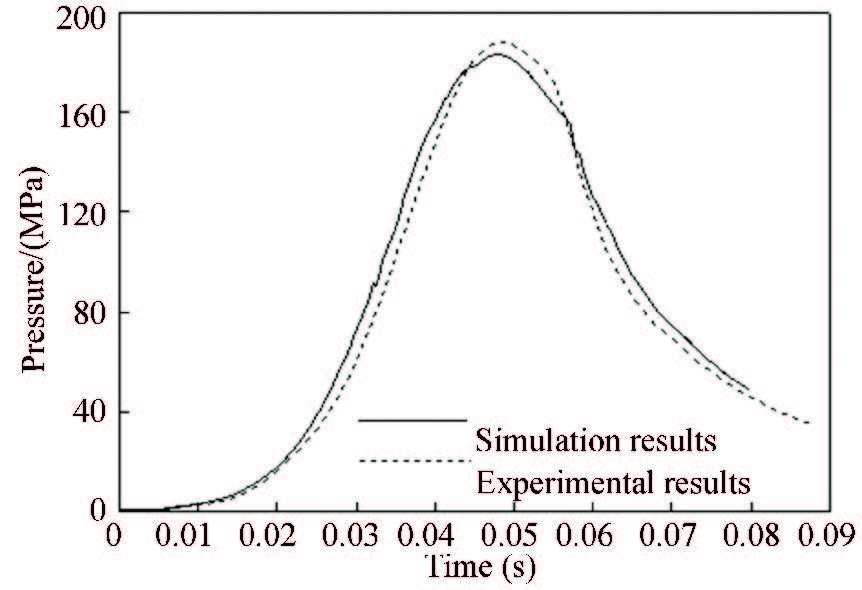
4.1 Comparison Between Numerical Simulation and CalculationThe numerical codes written with the C language are set with the same parameters as the tests.Figs. 4 and 5 show the pressure measured at 1# and 2# points of test 1 and the corresponding results obtained by simulation. Furthermore, the maximum pressure measured in the test is 152.6 MPa, and the muzzle pressure is 44 MPa, and the projectile velocity is 705 m/s.And the calculated results are 153.6 MPa, 48 MPa and 723 m/s. Figs. 6 and 7 show the pressure measured at 1# and 2# points of test 2 and the corresponding results obtained by simulation. In this test, the maximum pressure is 188.4 MPa, and the muzzle pressure is 35 Mpa, and the projectile velocity is 703 m/s.And the calculated results are 183.2 MPa, 43 MPa and 722 m/s. It can be seen from the above data and the pictures that the simulation results are basically close to the experimental results. The calculation velocity is slightly larger than the test result. It is due to the influence of muzzle flame, the test velocity is always measured at a certain distance from the muzzle. Therefore, the established discrete group gas-solid two phase flow model can approximately describe the launching process of the Davis gun. And the numerical codes are proved to be accurate and effective.
|
Figure 4 Curves of simulation and experimental pressure at 1# position (test 1) |
|
Figure 5 Curves of simulation and experimental pressure at 2# position (test 1) |
|
Figure 6 Curves of simulation and experimental pressure at 1# position (test 2) |

|
Figure 7 Curves of simulation and experimental pressure at 2# position (test 2) |
4.2 Motion of the Tubular Powder Beams
In Section 4.1 the discrete group two-phase flow model has been verified to be available. So the simulation can be used in analyzing the propellant motion in the charge. The velocity curves of the 9 tubular powder modules are shown in Fig. 8, which is gained by simulating with the parameters of test 1. It can be seen from Fig. 8 that the velocity of the powder modules are all kept in a low level at the beginning of the launching process. It represents that the pressure wave is stable and the designed Davis gun system is safe and reliable. The location of each tubular powder module in test 1 is shown in Fig. 9. It can be seen that the propellant beams moving trend is to the bottom of the projectile and the bottom of the balance block. Because the displacement of the projectile increased sooner than the balance block, most of the propellant beams are assembled to the bottom of the projectile, and moved together with the projectile.But we can also find that there is no apparent accumulation appeared in this process.

|
Figure 8 Velocity curves of the 9 tubular powder modules |

|
Figure 9 Location curves of the 9 tubular powder modules |
5 Conclusions
In general, the interior ballistic process is much more complex due to the movement of two objects in two directions and the large amount of tubular powder modules as the propellant. In this paper, a new one-dimensional discrete group gas-solid two-phase flow model is developed for simulation.As shown in Section 3, the simulation results are consistent with experimental data. The new discrete group two-phase flow model can be used in revealing characteristics of the flow filed and the basic rules of the motion of the tubular propellant in Davis gun, and it is theoretically significant for the further study on the interior ballistic performance of the large caliber high speed Davis guns.
The discrete group two-phase flow model in this paper is a one-dimensional model of the ideal case, without considering the radial effects and other factors.In the further studies, we will establish a two-dimensional model, describing the motion of the propellant and the distribution of flow field completely and accurately.
| [1] |
Zhang B Z, Wang H, Wang S S, et al. One-dimensional two-phase flow modeling and simulation for interior ballistics of large-caliber Davis gun. Journal of Ballistics, 2014, 26(1): 17-21. ( 0) 0)
|
| [2] |
Kathe E L.Rarefaction Wave Gun Propulsion(RAVEN). NewYork:Rensselaer Polytechnic Institute, 2002.
( 0) 0)
|
| [3] |
Xu L E, Li Y C, Gao L N. Shooting security analysis of counter-mass propelling gun with large caliber and high muzzle velocity. Journal of Unversiy of Science and Technology, 2008, 38(11): 1304-1309. ( 0) 0)
|
| [4] |
Duan J Y, Wang Y P, Liu C L, et al. The preliminary study of improving Davis gun launching capability. Chinese Journal of High Pressure Physics, 2008, 22(1): 108-111. ( 0) 0)
|
| [5] |
Peng H X. Analysis of pressure distribution in chamberof gun for balance. Journal of Nanjing Institute of Industry Technology, 2005, 5(2): 28-31. ( 0) 0)
|
| [6] |
Weng C S, Jin Z M, Yuan Y X. Interior bal1istics model and its numerical simulation for stick-Propellant bundles. Journal of Ballstics, 1993(3): 1-7. ( 0) 0)
|
| [7] |
Cheng C, Zhang X B. Two-dimensional numerical simulation on two-phase flow interior ballistic performance of a guided projectile. Acta Armamentarii, 2015, 36(1): 58-63. ( 0) 0)
|
| [8] |
Cai C W, Zhang Y R, Tao C L, et al. Study on interior ballistic performance for a new type of guided projectile by gun. Bulletin of Science and Technology, 2014, 30(7): 92-95. ( 0) 0)
|
| [9] |
Li H Q, Zhang X B, Wang Y. Two phase flow numerical simulation of interior ballistics of the series chamber gun. Acta Armamentarii, 2012, 33(5): 513-518. ( 0) 0)
|
| [10] |
Yuan Y X, Zhang X B. Harbin:Harbin Institute of Technology Press. 2005, 277-279.
( 0) 0)
|
| [11] |
Zhang X B, Weng C S, Yuan Y X, et al. An axisymmetrical particle trajectory model and its simulation. Journal of Ballistics, 1997, 9(1): 60-64. ( 0) 0)
|
| [12] |
Yuan Y X, Yang J Y. An interior ballistic discrete particle model and its numerical calculation. Acta Armamentarii, 1996, 17(3): 198-201. ( 0) 0)
|
| [13] |
Peng H X. Analysis of pressure distribution in chamber of gun for balance. Journal of Nanjing Institute of IndustryTechnology, 2005, 5(2): 28-31. ( 0) 0)
|
| [14] |
Tao R Y, Sun J B, Huang M, et al. Interior ballistics numerical simulation and experiment on balance gun with low and high pressure chamber. Journal of Nanjing University of Science and Technology, 2006, 30(4): 478-485. ( 0) 0)
|
| [15] |
Ji X S, Wang H, Feng G Z, et al. Experimental research on technology of multi-point ignition in large caliber gun withhigh muzzle energy. Journal of Ballistics, 2010, 22(4): 67-69. ( 0) 0)
|
| [16] |
Jiang S Y, Ji X S, Wang H, et al. Multi-point ignition characteristics in large caliber balance gun propellant with long-chamber charges. Chinese Journal of Energetic Materials, 2015, 23(5): 477-483. ( 0) 0)
|
| [17] |
Jin Z M. Beijing: Beijing Institute of Technology Press. 2004, 78-79.
( 0) 0)
|
| [18] |
Weng C S, Wang H. Beijing:National Defence Industry Press. 2006, 65-67, 79, 190.
( 0) 0)
|
| [19] |
Wang S C, Zhou Y H, Liu Q L, et al. Beijing:Ordnance Industry Press. 1992.
( 0) 0)
|
| [20] |
Anderson J D. Beijing:Chinese Machine Press. 2007, 315-316.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


