Phased array radarcan switch the beam direction rapidly by disposing the phase shifter with a wave controller. This overcomes the radar capability limit caused by the beam's rotating inertia of mechanical scanning antenna. It is also due to the high beam agility of the phased array radar that presents new challenges to beam detection and makes it impossible to detect the radar signal with conventional methods[1]. The present studies of beam detection mainly focus on the technical parameters and the radiation source classification of emitted signals. There are mainly two kinds of signal classification. One kind of classification is to establish the emitter database based on prior knowledge and related model techniques to realize signal classification[2], which has higher dependability but at the same time has more difficulty in building up the database due to the antagonistic features of reconnaissance. The other kind of classification is the pattern recognition method typical of the rough sets theory [3], which is less dependable on prior knowledge but has lower dependability.
As the received pulse amplitude is not only dependent on transmitting antenna but also on receiving antenna, in signal processing of electronic reconnaissance, pulse amplitude information of PAR is generally abandoned [4-5]. However, pulse amplitude information is closely related to the working state of the radar and scanning manner of the beams, which is the reason why relevant researches have been going on in recent years. In one example, by analyzing the impacts of phased array radar's beam scanning on reconnaissance and interception, the interception probability is calculated during frequency hopping[6]. In another example, a reconnaissance method of recognizing the main beam's direction is provided based on the side-lobe distortion during the beam scanning of phased array radar[7]. These researches cover only the reconnaissance methods of regular beam scanning when the phased array radar is in the state of searching. However, the missions of phased array radar beam, especially the guidance radar, is applied not only to target searching, but also to such simultaneous tasks as multi-channel target searching, complementary searching, tracking and missile guiding for several different targets[8-10]. In this paper, the radar emission signals received from a specific coordinate point is analyzed according to missions of guidance radar beam.
2 Analysis of Phased Array Radar 2.1 Phased Array Radar Antenna Pattern ModelAccording to the antenna theory, the antenna voltage pattern is formulated as[11]
| $G\left( {\theta ,\varphi } \right) = D\left( {\theta ,\varphi } \right) \cdot \left| {{F_a}\left( {\theta ,\varphi } \right)} \right| \cdot \left| {f\left( {\theta ,\varphi } \right)} \right|$ | (1) |
where D(θ,φ) is the direction factor; Fa(θ,φ) is the array factor; f(θ,φ) is the array element factor; θ and φ are the azimuth angle and the elevation angle respectively under the spherical coordinate of array plane,θ∈[-π/2,π/2],φ∈[-π,π].
When the beam points to (θ0,φ0), the direction factor D(θ0,φ0) can be expressed as:
| $D\left( {{\theta _0},{\varphi _0}} \right) = {\left[ {\frac{{4\pi A\eta }}{{{\lambda ^2}}} \cdot \left( {1 - {{\left| {\Gamma \left( {{\theta _0},{\varphi _0}} \right)} \right|}^2} - \left. {{L_\Omega }} \right) \cdot \cos {\theta _0}} \right)} \right]^{\frac{1}{2}}}$ | (2) |
where A is the antenna aperture area(m2);η is the amplitude weighting aperture efficiency; λ is the antenna working wavelength; θ0 is the angle from the beam direction to the array's normal line (scanning angle in the conventional sense, its unit being the rad); Γ(θ0,φ0) is the reflection coefficient when the antenna mismatches at beam direction (θ0,φ0) and LΩ is the synthetically ohmic loss of beam forming network.
For a two-dimensional rectangular array consisting of (2Nx+1)×(2Ny+1) antenna elements, distances between adjacent array elements are supposed to be dx on the X-axis and dy on the Y-axis respectively. The coordinate origin is located at element (0,0). The array factor of the two-dimensional array can be expressed as Eq.(3).
| ${F_a}\left( {\theta ,\varphi } \right) = \sum\limits_{m = - {N_x}}^{{N_x}} {\sum\limits_{n = - {N_y}}^{{N_y}} {{\mathop{\rm Im}\nolimits} n\exp \left( {{\rm{j}}k\left( {m{\rm{d}}x{\tau _x} + n{\rm{d}}y{\tau _y}} \right)} \right)} } $ | (3) |
where τx=sin θcos φ-sin θ0cos φ0; τy=sin θsin φ-sin θ0sin φ0; (θ0,φ0) is the beam direction; k is the number of beam positions (k=2π/λ); Imn are the weighting coefficients.
When the beam points to B(θ0,φ0), then
| $\begin{array}{ccccc} {F_a} & \left( {\theta ,\varphi ,{\theta _0},{\varphi _0}} \right) = {F_a}\left( {{T_x},{T_{x0}},{T_y},{T_{y0}}} \right) = \\ \sum\limits_{m = - {N_x}}^{{N_x}} {\sum\limits_{n = - {N_y}}^{{N_y}} {{\mathop{\rm Im}\nolimits} n\exp \left[ {{\rm{j}}k\left( {n{\rm{d}}x\left( {{T_x} - {T_{x0}}} \right)} \right.} \right.} } + \\ \left. {\left. {n{\rm{d}}y\left( {{T_y} - {T_{y0}}} \right)} \right)} \right] = {F_a}\left( {{T_x} - {T_{x0}},{T_y} - {T_{y0}}} \right) \end{array}$ | (4) |
where Tx0=sin θ0cos φ0,Ty0=sin θ0sin φ0.
According to Eqs.(1),(2) and (4), it can be seen that the power of the radar emission signals (amplitude) reflects not only the antenna pattern, but also its close relationship with the beam direction. The beam shape changes with beam direction change for a certain phase system, but its pattern can be decided when the beam points to fixed locations. Fig. 1 demonstrates the 3D pattern of the antenna and the azimuth pattern of phased array at elevation angle (0°,0°). Under constant emitter power, when the beam changes its direction continuously, the received pulse amplitude at a fixed point varies accordingly. In radar searching mode, by modeling and simulating the distribution variation of the power and analyzing its variation pattern at a certain coordinate point will help us to analyze effectively the direction information of the radar.

|
Figure 1 Antenna pattern of phased array |
2.2 Beam Tasks of Phased Array Radar
The beam searching model describes how the antenna beam changes along with time in the local coordinate system. This mathematical model expresses the way that radar searches possible targets in a given airspace. According to its missions, radar employs different searching methods to acquire optimal searching and detecting performance. With the fast conversion of the beam direction through beam control, phased array radar can accomplish the task of searching and tracking of any airspace with the scanning sector.
Supposed that antenna beam's dwell time is T. Δφ and Δθ are often defined as half power width at azimuth and elevation angle respectively. φ and θ are the azimuth and elevation ranges to be searched. Ts is total time spent in searching the whole airspace. So Ts can be represented as Eq.(5).
| ${T_s} = \frac{{\varphi \theta }}{{\Delta \varphi \Delta \theta }}T$ | (5) |
As the beam width of phased array varies with the scanning angle, a more accurate formula[12] of Ts is represented as Eq.(6).
| ${T_s} = {K_\varphi }{K_\theta }T$ | (6) |
where Kφ is the beam number covering the searched airspace at azimuth and Kθ is beam number at elevation.
Taking Kφ as an example for analysis and the calculation of Kθ is the same as that of Kφ. The relationship between Kφ and searched range at azimuth, that is,±φmax can be expressed as Eq.(7).
| ${K_\varphi } = 2{p_b} + 1$ | (7) |
where Pb is the beam number from normal line to direction φmax, and Pb is shown in Eq.(8).
| ${p_b} = \frac{{\rm{d}}}{\lambda }{2^k}\sin {\theta _{max}}$ | (8) |
Where k is the bit number of digital phase shifter.
The fast conversion of the beam is an important technical feature of the phased array radar. The radar can not only track multiple targets simultaneously, but also keep on searching surveillance airspace while tracking. The difference in tracking data rate (or tracking sample interval) of the same group of targets will greatly affect the accuracy of tracking performance. Generally speaking, the accurate target tracking data rate is about 10 Hz while the coarse one is about 1 Hz and the reconnaissance target data rate is about 0.1 Hz. Obviously, the higher the data rate is, the more time to use the radar is and therefore with more costs. A more reasonable solution is that different tasks are planned for different targets requirements[13]. Thus, the radar beam tasks can be planned as follows:
Supposed that the phased array radar is carrying out k missions including a searching task plus k-1 tracking tasks, the data rates are s1,s2,s3,…,sk and the corresponding sample intervals are T1,T2,T3,…,Tk. The sample intervals between the same task beams are integral multiple of radar beam's dwell time T. Beam intervals of every task can be shown as:
| ${T_i} = {N_i}T, i = 1,2, \cdots , k$ |
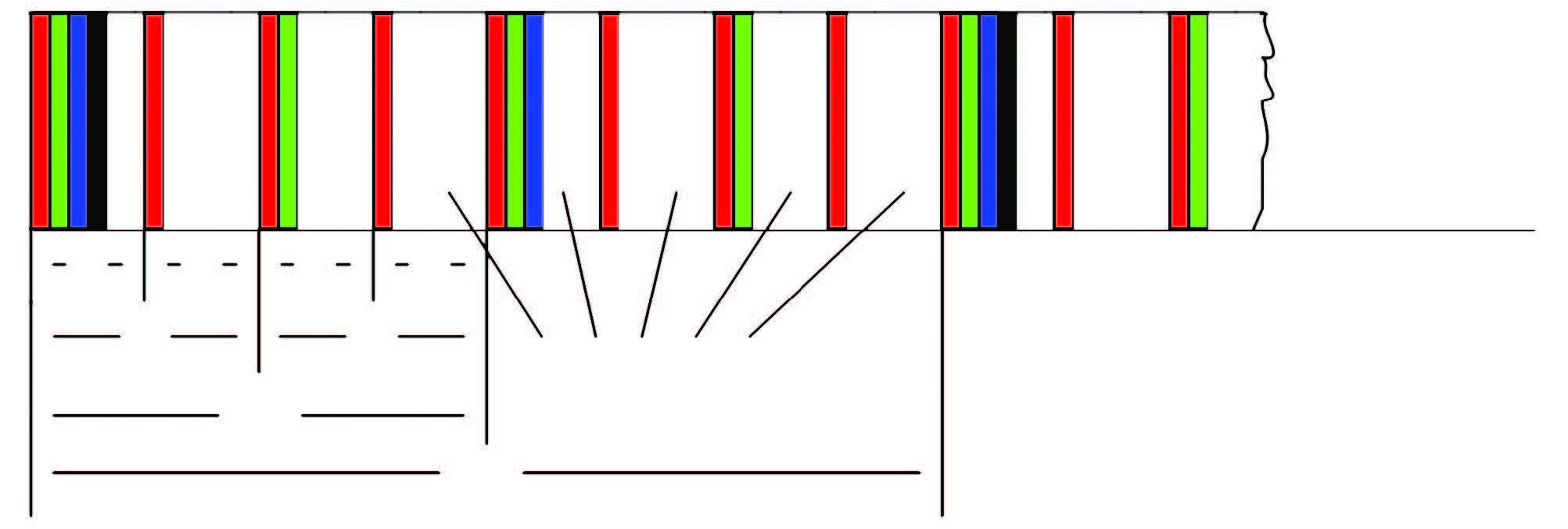
As shown in Fig. 2, the phased array radar has 4 tracking states where every state has their corresponding tracking intervals expressed as T1, T2, T3, T4. Tracking missions are generally accomplished by using time division for multiple targets tracking.
| $\left[ {\begin{array}{*{20}{c}} {{T_1} = {N_1}T}\\ {{T_2} = {N_2}T}\\ {{T_3} = {N_3}T}\\ {{T_4} = {N_4}T} \end{array}} \right]$ |
|
Figure 2 Relationship between searching time and tracking time under 4 tracking states |
Fig. 2 shows the relationship between searching time and tracking time under 4 tracking states. In each time interval, the radar first schedules tracking missions in every cycle period, and then use the remained time to searching airspace. From Fig. 2, we can see that the phased radar realizes its multiple missions with beam agility and time division.
3 Classification of Pulse Amplitude Sequence with Optimal ModelBy detecting the radar emission at the specific coordinate point and analyzing the power of the signals received, it can be easily seen that when the phased array radar is carrying out different tasks, the wave controller will direct the antenna to different directions. Then the radar emission power received at a specific coordinate point will fluctuate severely, which might be slow and continuous when the radar is doing the searching and vibrant when it is doing the tracking. The characteristic differs greatly with that of the traditional mechanical scanning radar and the pulse amplitude sequence of signals received lacks regularity[14-16].
Compared with the mechanical scanning radar, though the amplitude time series of the phased array radar signals received at the specific coordinate point fluctuate with no fixed laws, but amplitude sequence of the same mission has continuity because beams on one target vary continuously. Searching beams usually scan a given airspace continuously which is arranged by a specified manner, just like the example given above. When tracking targets, the radar needs to predict the next position of the target according to its current position and speed and so on, so that radar beam can keep up with target. Therefore, tracking beam moves along with target, that is, the movement of the tracking beam is determined by the target's continuous movement[17]. And the amplitude sequence is also continuous when radar is doing the tracking. But its continuity is not shown directly due to the reason that there are sometimes searching tasks when the radar is carrying out the tracking tasks.
From the analysis above, it can be seen that the pulse amplitude sequence received directly from a specific coordinate point is disorderly and discontinuous as a result of mixed beam missions, but its beam changes continuously and smoothly when divided into several sequences according to their missions. Besides, the beams at different task points are determined by the searched airspace and tracked targets positions, so it can conclude that the different missions' beams are mutually independent. Based on the two principles above, this paper builds up the optimal classification model with least-squares and curve-fitting methods.
In Cartesian coordinate system of phased array, the flight path of a target can be supposed in Eq.(9).
| $\left\{ {\begin{array}{*{20}{c}} {x = \alpha \left( t \right)}\\ {y = \beta \left( t \right)}\\ {z = \gamma \left( t \right)} \end{array}} \right.$ | (9) |
As is known to all, the target moves continuously in the air, and this movement is smooth except for some extreme cases such as large-angle maneuvering. As a result, the target's coordinate is a smooth and continuous function of time. According to spherical coordination conversion equation, Eq.(9) can be written as Eq.(10).
| $\left\{ {\begin{array}{*{20}{l}} {R = \sqrt {{\alpha ^2}\left( t \right) + {\beta ^2}\left( t \right) + {\gamma ^2}\left( t \right)} }\\ {\varphi = {{\tan }^{ - 1}}\left( {\frac{{\beta \left( t \right)}}{{\alpha \left( t \right)}}} \right)}\\ {\theta = {{\tan }^{ - 1}}\left( {\frac{{\sqrt {{\alpha ^2}\left( t \right) + {\beta ^2}\left( t \right)} }}{{\gamma \left( t \right)}}} \right)} \end{array}} \right.$ | (10) |
where R,φ and θ are distance, azimuth and elevation angles relative to origin of coordinates under phased array's spherical coordinate respectively.
The radar beam follows its target closely in order to keep a stable tracking of a target. The moving path of the beam under the same tracking mission canbe also considered as a smooth and continuous function of time. Amplitude sequence of radar radiated pulse can be treated as samples of equal time interval from this function when the radar keeps a constant detection data rate.
Supposed that the pulse amplitude sequence received at a fixed point is D1,D2,D3,…,DM, where any subsequence represents one mission that the radar is taking. Thus, the radar's signal amplitude sequence can be divided into ${\hat k}$ groups corresponding to its current ${\hat k}$ missions. If the maximum mission number of the phased array radar is W,1≤ ${\hat k}$ ≤W, the amplitude sequence can be classified as follows:
| ${D_1},{D_2},{D_3}, \cdots ,{D_M}\left\{ {\begin{array}{*{20}{l}} {{D_{11}},{D_{12}},{D_{13}}, \cdots ,{D_{1{M_1}}}}\\ {{D_{21}},{D_{22}},{D_{23}}, \cdots ,{D_{2{M_2}}}}\\ \vdots \\ {{D_{\left( {\hat k - 1} \right)1}},{D_{\left( {\hat k - 1} \right)2}},{D_{\left( {\hat k - 1} \right)3}}, \cdots ,{D_{\left( {\hat k - 1} \right){M_{\left( {\hat k - 1} \right)}}}}}\\ {\left\{ {{D_1},{D_2},{D_3}, \cdots ,{D_M}} \right\} - \left\{ \begin{array}{l} {D_{11}},{D_{12}},{D_{13}}, \cdots ,{D_{1{M_1}}},{D_{21}},{D_{22}},{D_{23}}, \cdots ,\\ {D_{\left( {\hat k - 1} \right)1}},{D_{\left( {\hat k - 1} \right)2}},{D_{\left( {\hat k - 1} \right)3}}, \cdots ,{D_{\left( {\hat k - 1} \right){M_{\left( {\hat k - 1} \right)}}}} \end{array} \right\}} \end{array}} \right.$ |
and Dij=Dm,m=M1+M2+…+Mi-1+j.
As the antenna pattern and the current beam point direction are unknown, it is difficult to estimate the amplitude sequence with the prior knowledge. Besides, the antenna pattern of the phased array radar may deforming the process of beam transformation [18-19], which may cause greater error to compute with a fixed antenna pattern. Based on the fact that the amplitude sequence of the radar beams under the same mission is smooth and continuous, the function of the radiated pulse amplitude approximates the Taylor expansion method according to Taylor Theorem, and the error between them is decided by the expansion order. Thus, elementary function can be used to approximate the function which represents the pulse amplitude transformation when the beam changes direction. Here, the polynomial function is adopted whose order is less than n, as is shown in Eq.(11).
| $y = \left| {{a_0} + {a_1}t + \cdots + {a_n}{t^n}} \right|$ | (11) |
For ${{\hat k}_i}$ mission and its subsequence Mi, Eq.(12) can be built up.
| $\left\{ {\begin{array}{*{20}{l}} {\left| {{a_0} + {a_1} \cdot 0 + \cdots + {a_n}{{\left( 0 \right)}^n}} \right| = {D_{i1}}}\\ {\left| {{a_0} + {a_1} \cdot \left( {{N_i}T} \right) + \cdots + {a_n}{{\left( {{N_i}T} \right)}^n}} \right| = {D_{i2}}}\\ {\left| {{a_0} + {a_1} \cdot \left( {2{N_i}T} \right) + \cdots + {a_n}{{\left( {2{N_i}T} \right)}^n}} \right| = {D_{i3}}}\\ \vdots \\ {\left| {{a_0} + {a_1} \cdot \left[ {\left( {{M_i} - 1} \right){N_i}T} \right] + \cdots + {a_n}{{\left( {\left( {{M_i} - 1} \right){N_i}T} \right)}^n}} \right| = {D_{i{M_i}}}} \end{array}} \right.$ | (12) |
When n <Mi, the least-squares method is used for curve fitting [20]. Coefficients ${{\hat a}_{i0}},{{\hat a}_{i1}},{{\hat a}_{i2}}, \cdots ,{{\hat a}_{in}}$ are counted with Eq.(13).
| $\left\| {{\delta _i}} \right\|_2^2 = \min \sum\limits_{j = 1}^{{M_i}} {\left\{ {{y_{ij}} - f\left[ {\left( {j - 1} \right){N_i}{T_i}} \right]} \right\}} $ | (13) |
Apart from being used for target tracking, the radar beam resources are also applied to the searching and surveilling of a given airspace. Then sum all errors of sequences, as in Eq.(14).
| $\left\| \delta \right\|_2^2 = \sum\limits_{i = 1} {\left\| {{\delta _i}} \right\|_2^2} $ | (14) |
As beams under different missions are mutually independent, this summation of all errors will increase when different missions' beams are sorted in one group for curve fitting. In the end, the optimal model is established with Function (15) as the kernel function.
| $\begin{array}{*{20}{c}} {\min {\rm{ }}\left\| \delta \right\|_2^2}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}{D_1},{D_2},{D_3}, \cdots ,{D_M}}\\ {1 \le \hat k \le W} \end{array}$ | (15) |
To verify the optimal model above, Phased Array Toolbox of MATLAB software is used to generate radiated pulse amplitude time sequence received at a fixed coordinate point when the phased array radar takes 4 tracking missions. In simulation (as shown in Fig. 3),200 radiated signal amplitude values are adopted during the radar works, where the beam dwell time is 5 ms.

|
Figure 3 Radiated pulse amplitude sequence of phased array |
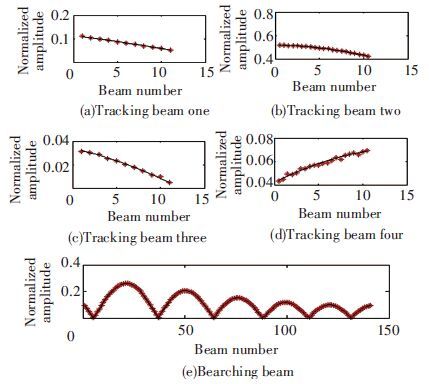
As is demonstrated in Fig. 3, the amplitude subsequence on the top is clearly continuous while that on the bottom is irregular with amplitude saltation edges between them. As the beam mission as shown in Fig. 4, when dividing the whole sequence into several groups, subsequences are took with fixed data rate as tracking beam radiated pulse amplitude sequences, and the remaining ones for searching beam. The Taylor expansion function with order not greater than 5 is adopted for subsequences curve fitting, and the pulse amplitude sequence is sorted with Function (15) as the objective function.
|
Figure 4 Classified radar radiated signal amplitude subsequences |
To reduce computation, more prior knowledge should be fully used to restrict optimization range. For the common targets, reasonable tracking data rate can be set as 5-30 times per second which will fully meet the requirements of rough tracking and precise tracking. Under this constraint, all five classes of optimization objective divided with least-squares classification model are able to obtain the minimum value. Data rates on 4 tracked targets are 10 times,20 times,10 times and 20 times per second respectively, and the remaining values are used for the target searching beam, as shown in Fig. 4.
In Fig. 4, after all the values in the pulse amplitude sequence are sorted, every tracking mission changes continuously with the target track and every searching mission fluctuates continuously with the space searching law. Besides, because of environment and system noise, non-point or leak point may appear in the received pulse amplitudes. There are two ways to improve it. One is to increase the receiver sensitivity and adopt pre-filtering to restrain out-of-band noise. The other one is to make full use of prior knowledge to increase not only the classification accuracy, but also the classification efficiency of the sequence data.
5 ConclusionsThis paper builds upan optimal model of pulse amplitude sequence of the phased array radar based on the fixed points in a certain space, which will effectively help distinguish the searching and tracking missions of the radar. However, when the radar works on multi-mission searches with different searching centers and sectors, both the frequency and the time domain of the pulse amplitude sequence received from the fixed points in a certain space are not distinctive and makes it difficult to classify more accurately the pulse amplitude sequence of the searching mission. Our further study in the future will focus on how to create more efficient kernel functions to describe the sequence characteristics and how to fuse reconnaissance data received at different points to increase the classification numbers and to improve classification precision. Considering that the reconnaissance system is mainly concerned about the tracking missions of the guidance radar, the sorting model of this paper does not include a fine classification of searching mission pulse amplitude sequence.
| [1] |
Wiley R G. ELINT: The Interception and Analysis of Radar Signals. Boston: Artech House, 2006. ( 0) 0)
|
| [2] |
Dudczyk J, Matuszewski J, Wnuk M. Applying the relational modelling and knowledge based techniques to the emitter database design. MIKON-2002 14th International Conference Microwave, Radar and Communication.. Piscataway:IEEE, 2002(1): 172-175. ( 0) 0)
|
| [3] |
Quan W, Li P, Xu F K. An algorithm of signal sorting and recognition of phased array radars. Proceedings of 2010 IEEE 10th International Conference on Signal Processing (ICSP). Piscataway: IEEE, 2010, 1877-1880. ( 0) 0)
|
| [4] |
Gustavo L R, Jesus G, Alvora S O. Digital channelized receiver based on time-frequency analysis for signal interception. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(3): 879-898. ( 0) 0)
|
| [5] |
Jang D S, Choi H L, Roh J E. Optimization of surveillance beam parameters for phased array radars. IET International Conference on Radar Systems (Radar 2012), 2012, 1-5. DOI:10.1049/cp.2012.1633 ( 0) 0)
|
| [6] |
Li X, Wang C Y, Wang Q. The method to reconnoiter the main beam direction of phased array radar based on the side beam surveying. Journal of CAEIT, 2013, 8(5): 507-511. ( 0) 0)
|
| [7] |
Wang X S, Xiao S P. Beijing:Publishing House of Electronics Industry. 2010, 195-197.
( 0) 0)
|
| [8] |
Gini F, Maio A D, Patton L. Herts: Institution Eng. Technol. 2011.
( 0) 0)
|
| [9] |
Melvin W, Scheer J. Herts: SciTech Publishing. 2012.
( 0) 0)
|
| [10] |
Hurtado M, Zhao T, Nehorai A. Adaptive polarized waveform design for target tracking based on sequential Bayesian inference. IEEE Transactions on Signal Processing, 2008, 56(3): 1120-1133. ( 0) 0)
|
| [11] |
Zhang Q G, Zhu Y Q, Pan Y F. Impacts analysis of phased array Radar's beam scanning on reconnaissance and interception. Journal of Air Force Radar Academy, 2012, 42(5): 318-321. ( 0) 0)
|
| [12] |
Zhang G Y. Beijing :National Defense Industry Press. 2009, 196-207.
( 0) 0)
|
| [13] |
Robertazzi T. Scheduling beams with different priorities on a military surveillance Radar. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 1725-1739. ( 0) 0)
|
| [14] |
Nishinuchi K, Kobayashi M. Improved algorithm for estimating pulse repetition intervals. IEEE Transactions on Aerospace and Electronic Systems, 2000, 56(3): 407-421. ( 0) 0)
|
| [15] |
Zeng D, Zeng X, Lu G, et al. Automatic modulation classification of Radar signals using the generalised time-frequency representation of Zhao, Atlas and Marks. IET Radar, Sonar and Navigation, 2010, 5(4): 507-516. ( 0) 0)
|
| [16] |
Lai W L, Kind T, Wiggenhauser H. Using ground penetrating Radar and time-frequency analysis to characterize construction materials. NDT&E International, 2011, 44(1): 111-120. ( 0) 0)
|
| [17] |
Pai P F. Online tracking of instantaneous frequency and amplitude of dynamical system response. Mechanical Systems and Signal Processing, 2010, 24(4): 1007-1024. ( 0) 0)
|
| [18] |
Hall W M, Barton D K. Antenna pattern loss factor for scanning Radars. Proceedings of IEEE, 1965, 53(9): 1257-1258. ( 0) 0)
|
| [19] |
Hall W M. Antenna beam-shape factor in scanning Radars. IEEE Trans. Aerospace and Electronic Systems, 1968, 4(3): 402-409. ( 0) 0)
|
| [20] |
Boyd S, Vandenberghe L. Cambridge: Cambridge University Press. 2004, 319-421.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


