2. Department of Information Management and Information System, Northeast Forestry University, Harbin 150040, China
Protein-protein interaction (PPI) network is fundamental to research into the protein functions[1-3], functional pathway[4-5], protein complex[6-9] and disease gene prioritization[10-11]on a system level. In the past several years, numerous PPIs were generated by high-throughput experimental techniques and computational approaches. However, even if the organism is extensively studied, there are still a lot of PPIs to be discovered while some discovered PPIs are spurious[12-16]. This is even worse if the organism is new sequenced or the studies about the organism are just beginning. Thus, it is significant for further research of organisms to construct complete and reliable PPI networks of them.
As far as we known, domains are very commonplace in proteins and can bridge PPIs by interactions between them[17-18]. Additionally, domain composition of a protein is easy to identify by mature computational tools like HMMER[19]. Moreover, the majority of proteins in known reliable PPI database have domains, such as DIP[20], BioGrid[21], STRING[22]and IntAct[23]. Taking DIP as an example, the number of proteins containing domains and the number of PPIs that the two interacting protein both contain domains are listed in Table 1. It can be seen that above 85% PPIs are composed of proteins containing domains and above 90% interacting proteins have domains. Therefore, domains may be favorable clues to constructing PPI networks.
| Table 1 Proteins and PPIs of model organisms in DIP from the perspective of domain |
2 Related Works
Recently, some researches have been focused on predicting PPIs based on domain-domain interactions (DDI) or interactions between domain combinations[17-18, 24-28]. For example, Huang et al.[26]modeled the relationship of PPI, domain composition of proteins, DDI as a Maximal Specificity Set Cover problem (MSSC). So their method is named MSSC for short in the paper. In the method, a group of known PPIs were selected as positive PPIs and then the greedy algorithm was applied to find a set of DDIs to explain the selected positive PPIs to the largest degree of specificity. At last, some PPIs were inferred according to the set of DDIs. MSSC provided a novel way of predicting PPIs, but the selected positive PPIs may only cover a limited amount of proteins and it is prone to make the potential DDIs misjudged. Thus, the limitations of the selected positive PPIs may affect the performances of MSSC heavily.
Jang et al. [27] proposed a method based on Domain Cohesion and Domain Coupling, which is called DCC for short in this paper. In the method, domain cohesion represented the possibilities of domain combinations within single proteins and domain coupling represented the interacting probabilities of two domain combinations. They constructed an interaction significance (IS) matrix and a matrix element shows the interacting probability of two domain combinations. And then, the IS matrix was used to estimate possibilities of PPIs. In DCC, 2n-1 different domain combinations would be obtained from a protein with n domains. Therefore, (2n-1) × (2m-1) pairs of different domain combinations would be constructed based on domain composition of a protein with n domains and a protein with m domains and the IS matrix would became as an (2n-1)-by-(2m-1) matrix too. Obviously, IS matrix would be dramatically complex while it confronted two proteins with multiple domains. So DCC suffered from high computational complexity and less efficient.
3 Materials and MethodsTo overcome problems of the previous methods, we make inferences of PPIs through following steps. Firstly, a numerous pairs of domains are generated according to domain composition of proteins. Secondly, the pairs of domains are filtered by statistical significance tests. The pairs with high significance are used to identify potential PPIs to enlarge the original network. However, this also brings spurious PPIs to the network. To remove spurious PPIs, many candidate DDIs across proteins are constructed by combining domains of interacting proteins. After that, some candidate DDIs are selected as the real mediators of PPIs by statistical significant tests and used to reassess PPIs. Finally, the PPIs with low probabilities are removed and the remained PPIs are organized as a new network.
3.1 Selecting DDIs Based on Domain Composition of ProteinsAs reported, two domains which frequently co-exist in the same protein are very likely to collaborate with each other when they exist in different proteins[29-30]. It is the theoretical foundation that DDIs can mediate PPIs. Similarly, we consider that two domains may interact with each other if they co-exist frequently in single proteins. In another words, a pair of domains which frequently appears in single proteins may represent a DDI.
To collect pairs of domains as much as possible, pfam domain composition of all proteins in UniProt are downloaded from PFAM[31] database (ftp://ftp.ebi.ac.uk/pub/databases/Pfam/releases/swissprot.gz). In our method, two rules are applied to collect pairs of domains on the basis of domain composition of proteins. Proteins are usually folded into complex structures in the cell, so the number and order of domains may have little impact on DDIs. For this reason, the first rule is that the pairs which are composed of two different domains of a protein will be collected. Considering some domains often appear many times in proteins, the second rule is that the pairs which are comprised of two same domains of a protein will be also collected. For clear, the toy example in Fig. 1 demonstrates how to collect pairs of domains based on domain composition of a protein. In Fig. 1, a protein contains four domains which are represented by different shapes, and two domains are the same. According to our rules, three pairs which are composed of two of the three different domains and a pair which consist of the two same domains are collected. Totally, four pairs of domains are collected based on domain composition of the protein. In the light of the two rules, a number of pairs of domains are collected based on domain composition of all proteins in UniProt. However, most of the collected pairs of domains are not real DDIs. Because some domains just appear together by accident, they are not likely to interact with each other. For this reason, it is very necessary to distinguish the real DDIs from the collected pairs of domains.
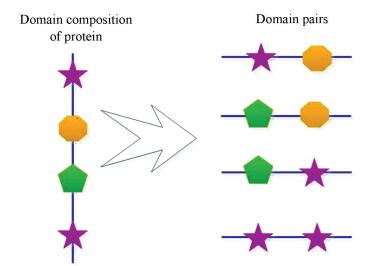
|
Figure 1 A toy example of collecting pairs of domains based on domain composition of a protein |
To identify DDIs, statistical significance tests are performed on the pairs of domains and the statistically significant pairs of domains are remained as real DDIs. In our method, p-value of a pair of domains x and y is represented by Pdp (x, y) and computed by formula (1), where Xp is the number of proteins which contain both domain x and y; Mp is the number of proteins containing domain x; Kp is the number of proteins containing domain y; Np is the number of proteins containing domains. To account for the multiple hypotheses testing, q-values [18] of the pairs are computed based on their p-values. Finally, the pairs of domains with q-value < 10-3 are remained and others are discarded. The remained pairs of domains are termed as “selected DDIs” in the following sections.
| $ {P_{{\rm{dp}}}}\left( {x,y} \right) = 1 - \sum\limits_{i = 0}^{{X_{\rm{p}}}} {\frac{{\left( {\begin{array}{*{20}{l}} {{K_{\rm{p}}}}\\ i \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{N_{\rm{p}}} - {K_{\rm{p}}}}\\ {{M_{\rm{p}}} - i} \end{array}} \right)}}{{\left( {\begin{array}{*{20}{l}} {{N_{\rm{p}}}}\\ {{M_{\rm{p}}}} \end{array}} \right)}}} $ | (1) |
Meanwhile, the number of the collected pairs of domains is largely less than the number of them in theory. It may suggest that domains have biases to interact with others. The biases of domain x interacting with domain y can be measured by conditional probability of y given x, cp(y|x). Given that N(·) is the number of proteins containing the given domain or pair of domains, cp(y|x) can be measured by ratio of N(xy) against N(x). Generally, two domains are very likely to interact if they both have high biases to interact with the other. Thus, formula (2) are designed to measure probability of a DDI(x, y) based on cp(y|x) and cp(x|y).
| $ \begin{array}{l} I{P_d}\left( {x,y} \right) = \sqrt {cp\left( {x|y} \right).cp\left( {y|x} \right)} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {\begin{array}{*{20}{l}} {\sqrt {\frac{{N\left( {xy} \right).N\left( {xy} \right)}}{{N\left( x \right).N\left( y \right)}}} ,}&{x \ne y}\\ {\frac{{N\left( {xy} \right)}}{{N\left( x \right)}},}&{x = y} \end{array}} \right. \end{array} $ | (2) |
where IPd(x|y) is big if and only if both cp(y|x) and cp(x|y) are big. In fact, formula (2) is a stringent measure of interacting possibility of two domains.On the whole, the bigger IPd(x|y) means that domain x and y has high possible to interact with each other. The interacting probabilities of two domains may influence their abilities to bridge PPIs. Therefore, it should be considered when PPIs are predicted based on DDIs.
3.2 Mining PPIs Based on DDIs to Enlarge the NetworkTo find the potential PPIs, it is hypothesized that two proteins may interact if at least one DDI can be modeled by their domains. Accordingly, many pairs of proteins are constructed based on the selected DDIs and regarded as candidate PPIs.
To select real positive PPIs, probabilities of the candidate PPIs are estimated based on interacting probabilities of the selected DDIs. It is believed that two proteins are very likely to interact with each other if the domains of one protein are prone to collaborate with the domains of the other protein. Thus, the interacting probability between two proteins X and Y, IPp(X, Y) is measured by formula (3), where D(.) represents the set of domains of the given protein and U represents the set of all domains.
| $ I{P_{\rm{p}}}\left( {X,Y} \right) = \frac{{\sum\limits_{{d_i} \in D\left( X \right),{d_j} \in D\left( Y \right)} {I{P_d}\left( {{d_i},{d_j}} \right)} }}{{\sum\limits_{{d_m} \in D\left( X \right) \cup D\left( Y \right),dn \in U} {I{P_d}\left( {{d_m},{d_n}} \right)} }} $ | (3) |
where the ratio that probabilities of DDIs between the two proteins against probabilities of all possible DDIs across the two proteins is used to measure interacting probability of the two proteins. The bigger IPp(X, Y) means that the two proteins are more likely to interact with each other. On our experiences, the PPIs with probability > 0.25 are remained as real positive PPIs.
Although these remained PPIs can enlarge the original network, they also bring noises into the original network.It is because that every the selected DDI cannot mediate PPIs as expected. For example, a DDI cannot mediate PPIs if the DDI only exists within protein.In other words, only the DDIs across two proteins can bridge interaction between two proteins.Therefore, some PPIs discovered by previous strategy are not likely to happen at all in practice.To remove these false positive PPIs, it is necessary to identify DDIs across proteins, which are the real mediators of PPIs.
3.3 Finding DDI Across Proteins Based on the Enlarged PPI NetworkTo identify DDI across proteins, all PPIs of the enlarged PPI network are analyzed again. For short, DDI across proteins is termed as DIA. It is believed that domains of a protein may interact with domains of the protein’s partners. As displayed by Fig. 2, several pairs of domains across proteins X and Y are collected by combining domains of X and Y. In Fig. 2, the interacting proteins are represented by blue lines with different shapes and the shapes denote different domains. For short, the pair of domains across proteins is termed as DPA and a DPA is regarded as candidate DIA. Accordingly, a great number of DPAs can be collected based on domain composition of interacting proteins in the enlarged network.
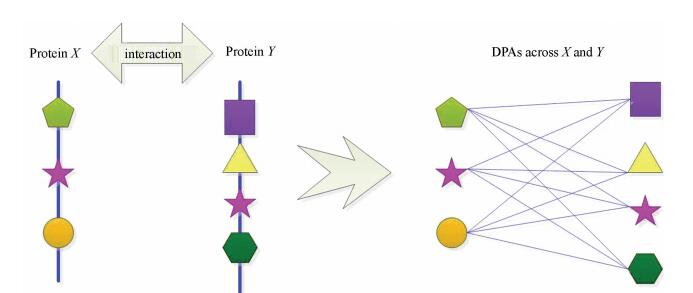
|
Figure 2 An example of collecting DPAs based on domain composition of interacting proteins X and Y |
To distinguish DIAs from the DPAs, p-values of the DPAs are measured by formula (4). In the formula, Pi(x, y) represents p-value of a DPA(x, y); Xi is the number of PPIs which can generate DPA(x, y); Mi is the number of PPIs which can generate DPA containing x; Ki is the number of PPIs which can generate DPA containing y; Ni is the total number of PPIs in the enlarged network. Based on the p-values, q-values of the DPAs are estimated and the DPAs with q-value < 10-3 are remained as DIAs.
| $ {P_i}\left( {x,y} \right) = 1 - \sum\limits_{j = 0}^{{X_i}} {\frac{{\left( {\begin{array}{*{20}{l}} {{K_{\rm{i}}}}\\ i \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{N_i} - {K_i}}\\ {{M_i} - i} \end{array}} \right)}}{{\left( {\begin{array}{*{20}{l}} {{N_i}}\\ {{M_i}} \end{array}} \right)}}} $ | (4) |
Next, the probabilities of DIAs are estimated based on the enlarged network. For a DIA(x, y), its probability is marked as IPa(x|y) and can be measured by formula (5). In formula (5), the meanings of symbols Ki, Mi and Xi are the same as those in formula (4). Formula (5) is designed under the assumption that two domains are very likely to form a DIA if the DPA is frequently appears across two interacting proteins. The bigger the IPa(x|y) is, the higher possible domain x and y interact to mediating PPIs. This information will be used to refine the enlarged PPI network.
| $ I{P_a}\left( {x,y} \right) = {\left( {\frac{{X_i^2}}{{{K_i} \cdot {M_i}}}} \right)^{\frac{1}{2}}} $ | (5) |
As discussed in Section 3.2, the enlarged PPI network may include many false positive PPIs.Two proteins are very prone to interact with each other if they satisfy two conditions: (1) there exist at least one DIA between them; (2) the domains of them are more likely to interact with each other than with domains of other proteins. Thus, the PPIs which cannot meet condition (1) are excluded from the enlarged PPI network at first. To give intuitive judgments on condition (2), probabilities of the remained PPIs are estimated based on probabilities of the DIAs.
Accordingly, as displayed in Fig. 3, a novel algorithm is put forward to measure probabilities of PPIs. In our algorithm, DIAs related to the two interacting proteins X and Y are grouped into three types: DIAs across X and Y, signed as ψ; DIAs across X and others, marked as Ф; DIAs across Y and others, denoted as Q. For a PPI(X, Y), its probability, P(X, Y) can be measured by the ratio of the total probabilities of the first type DIAs against the probabilities of all DIAs. The bigger the P(X, Y) is, the more possible proteins X and Y interact with each other. Generally, PPIs with probability bigger than a threshold are thought as reliable PPIs. As a matter of experience, the threshold is set as 0.25.Through the above steps, PPIs which satisfy the two conditions are remained and the others are excluded from the enlarged PPI network.

|
Figure 3 The algorithm for measuring probabilities of PPIs based on DIAs |
To make our algorithm easy to understand, Fig. 4 are used to introduce a simple example of computing probability of PPI here. In Fig. 4, proteins X and Y are represented by distinct irregular shapes respectively; domains are shown by a circle; edges denote interaction between domains and values on the edges are possibilities of DIAs. In addition, three types of lines display three different groups of DIAs. The detail process of computing probability of PPI(X, Y) is also displayed in Fig. 4.
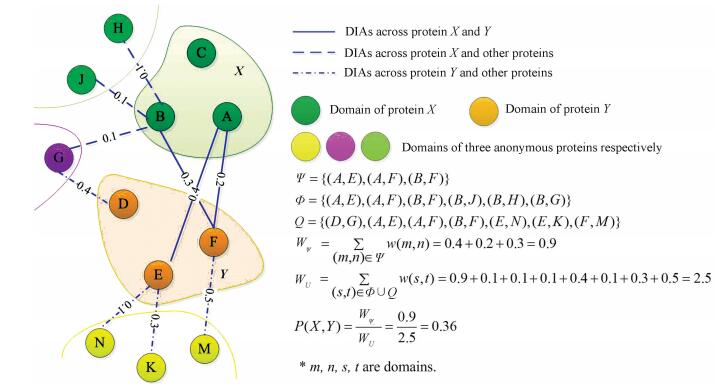
|
Figure 4 An example of computing probability of PPI(X, Y) |
4 Results and Discussion
In this section, all assumptions and steps of our method are validated to show their reasonability and effectiveness. And then, our methods are compared with the state-of-art works in this field to assess its performances.
4.1 Relationship of DDIs and Frequently Appeared Pairs of DomainsIn this article, we consider that two domains may interact with each other if they frequently coexist in proteins. To prove this assumption, a database of three-dimensional interacting domains (3did)[32] is used as the gold standard DDI set. 3did provides 8651 high credible DDIs which are identified by their high resolution three-dimensional structures (http://3did.irbbarcelona.org/).
The DDIs identified by our method are compared with the 8651 DDIs of 3did. Results of the comparison are listed in Table 2, where 3did represents the DDIs in 3did database; DPW represents the pairs of domains within proteins; DDI represents the identified DDIs by our method; num means the number of DDIs in each dataset; same_3did means the number of DDIs which are the same as those in 3did database. cov is the ratio of the same_3did and num of 3did, which means the recall of our inferences. For only a small fraction of positive DDIs are recorded in the 3did database, when, it is difficult to determine whether the DDI is positive or not if a DDI is not recorded in the 3did database. Thus, it may be not rigorous to estimate precision of our method by ratio of same_3did again num of DDI. However, the intersection of the 3did and DPW can be regarded as a sample of all positive DDIs, and the precision of our method can be estimated based on the sample. In our experiments, the same_3did of DDI represents the intersection of 3did and DDIs identified from the DPW by statistical significance tests. Thus, the ratio of same_3did of DPW and same_3did of DDI is regarded as the precision of identifying DDIs from domain pairs by statistical significance tests, which is marked as acc in Table 2. This strategy is also used in the comparisons of following experiments.
| Table 2 Compare DDIs inferred based on domain composition of proteins with those of 3did |
As shown in Table 2, 220748 pairs of domains are collected based on domain composition of proteins in UniProt database. These pairs capture 5413 DDIs of 3did and cover 62.57% of 3did. It may suggest that a pairs of domains which frequently appeared in protein is very likely to be a DDI. Through statistical significance tests, 54519 pairs of domains are selected from the 220748 pairs of domains and regarded as positive DDIs. The selected DDIs capture 4605 DDIs of 3did and cover about 53.23% of 3did. Considering 3did is a sample of positive DDIs, 4605/5413≈85% of positive DDIs are identified by statistical significance tests. It suggests that statistical significance tests are effectiveness on detecting DDIs from the pairs of domains.
4.2 Testing PPIs and Quality MeasuresIn the following section, a series of experiments will be performed on a group of PPIs for testing.Thus, the testing PPIs and quality measures are introduced here.
For our method relies on domain composition of proteins, PPIs of which the two interacting proteins both contain domains are chose from DIP, IntAct and high reliable BioGrid for testing.For unity, the UniProt accessions are used as protein identifiers.Finally, 47 495 testing PPIs involving 19 288 proteins are collected.
In our experiments, Gene Ontology (GO) annotation similarities of interacting proteins are employed to assess quality of PPIs. According the “guilt by association” rule, the interacting proteins usually share some functions, take part in the same biological process or localize in the same cellular component. Therefore, Pearson Correlation Coefficient (PCC) of probabilities and GO annotation similarities of PPIs is used as the quality measure of our comparisons and measured by formula (6).
| $ PCC = \frac{{\sum\limits_{i = 1}^n {\left( {{P_i} - \overline P } \right)\left( {{S_i} - \overline S } \right)} }}{{\sqrt {\sum\limits_{i = 1}^n {{{\left( {{P_i} - \overline P } \right)}^2}} } \cdot \sqrt {\sum\limits_{i = 1}^n {{{\left( {{S_i} - \overline S } \right)}^2}} } }} $ | (6) |
where Pi is the probability of the ith PPI in the testing set and P is the mean of probabilities of all testing PPIs; Si is the GO annotation similarity between interacting proteins of the ith PPI and S is the mean of GO annotation similarities of all testing PPIs. The bigger the PCC is, the higher the quality of the PPIs is, and vice versa. To compute GO similarities, annotations of the interacting proteins are downloaded from GO website (http://www.geneontology.org/) on July, 2014. GO similarities of the testing PPIs are computed by SORA[33] on three aspects separately: molecular function (MF), biological process (BP) and cellular component (CC).
After data preprocessing, over 80% of testing PPIs have GO similarities and the details are listed in Table 3 as follows. In Table 3, #PPI is the total number of the testing PPIs; #protein is the number of the interacting proteins; #PPIs_P, #PPIs_F and #PPI_C are the numbers of PPIs which have GO similarities on BP, MF and CC respectively.
| Table 3 Numbers of testing PPIs, proteins and testing PPIs with GO similarity |
4.3 Impact of Interacting Biases of Domains on PPIs
In our method, interacting biases of domains are considered when the probabilities of PPIs are computed.To show their influences on PPIs, the probabilities of testing PPIs are computed based on the 54519 DDIs which are predicted from domain compositions of proteins in Section 4.1 by two strategies separately. The first strategy ignores interacting biases of domains and set the probabilities of 54519 DDIs as 1 and then measures the probabilities of testing PPIs by formula (3). The second strategy computes the probabilities of 54519 DDIs based on interacting biases of domains by formula (2) and then measures the probabilities of testing PPIs by formula (3). Then, PCCs of probabilities and similarities of the testing PPIs under the two strategies are estimated by formula (6) and compared. Results of the comparisons are listed in Table 4, where “improvement” represents improvements on PCCs of the second strategy against those of the first strategy. It can be seen that PCCs of the second strategy are all higher than those of the first strategy on the three GO aspects.Compared to the first strategy, the second strategy improved 13%-22% on PCCs of probabilities and GO similarities. It supports that interacting biases of domains have positive impact on predicting PPIs. It also suggests that the second strategy is more effective on predicting PPIs than the first strategy.
| Table 4 Compare PCCs of GO similarities and probabilities of the testing PPIs |
To assess the ability of finding PPIs, the 54519 DDIs are employed to identify potential interactions between the 19288 testing proteins under the second strategy. The results are displayed in Table 5, where PPI_sim represents the testing PPIs with similarity on the specific GO aspect; PPI_pred represents the testing PPIs which can be detected based on the DDIs and have GO similarities; “Coverage” is the ratio of the number of PPI_pred against the number of PPI_sim, which means the recall of inferring PPIs based on the DDIs.
| Table 5 Compare PPIs that detected based on DDIs and PPIs with GO similarities |
From Table 5, it can be seen that only 14%-18% of the testing PPIs can be detected based on the 54519 DDIs. Whereas, a total of 125206 PPIs are predicted based on the 54519 DDIs in reality. This may be suggested that detecting PPIs based on the DDIs bring a large rate of spurious PPIs. We guess the spurious PPIs may be mediated by DDIs within proteins. It is inevitable for inferring DDIs from domain pairs in same proteins. However, these spurious PPIs can be reduced by DDIs across proteins. This is the reason why we find DDIs across proteins in our method.
4.4 Validations of DDIs Across ProteinsTo validate DDIs across proteins, potential interactions between the 19288 testing proteins are detected based on the 54519 DDIs. The potential PPIs and the testing PPIs are used to collect DPAs by combining domains of interacting proteins. Next, many DIAs are selected from the DPAs by statistical significance tests.
To evaluate quality of the selected DIAs, they are compared with DDIs of 3did database. Results of the comparison are listed in Table 6, where 3did represents DDIs in 3did database; DPA represents the pairs of domains across interacting proteins; DIA represents the DDIs across proteins; num means the number of DDIs in each dataset; same_3did means the number of DDIs which are the same as those in 3did database. cov is the ratio of the same_3did and the num of 3did, which means the recall of our inferences. acc equals the ratio of same_3did of DIA against same_3did of DPA. acc means the precision of selecting DIA from DPA by statistical significance tests.
| Table 6 Compare DDIs across proteins with DDIs of 3did |
As shown in Table 6, 96540 DPAs are collected from the potential PPIs and the testing PPIs. These DPAs capture 4783 DDIs of 3did and cover 55.29% of 3did. Through statistical significance tests, 56698 DPAs are selected from the 96540 DPAs and regarded as DIAs. Among these DIAs, 4474 DIAs are the same as DDIs of 3did and cover about 51.72% of 3did. So, it is feasible that inferring DDIs across proteins from domain composition of interacting proteins. As well, about 93.54% of same_3did of DPA are selected by statistical significance tests. It may suggest that statistical significance tests do well in detecting DIAs from DPAs.
To assess the impact of the potential PPIs on finding DIAs, two strategies are applied to estimate probabilities of the testing PPIs. The first strategy finds a set of DIAs based on the testing PPIs and measures probabilities of the testing PPIs. The second strategy finds DIAs based on the testing PPIs and the potential PPIs, and then computes probabilities of the testing PPIs based on the DIAs. Finally, PCCs of probabilities computed by the two strategies and GO similarities of the testing PPIs on BP, MF and CC are measured respectively and compared. Results of the comparisons are listed in Table 7, where “improvement” represents the improvement on PCCs of probabilities of the 2nd strategy against the 1st strategy. Obviously, it can be seen that PCCs under the 2nd strategy are higher than those under the 1st strategy. It may suggest that the potential PPIs have great positive impact on finding DIAs and they are useful supplement of the testing PPIs.
| Table 7 Compare PCCs of GO similarities and probabilities of testing PPIs under the two strategies |
Additionally, the probabilities of DIAs under the second strategy are estimated by formula (5). To judge the impact of these probabilities on PPIs, the probabilities of the testing PPIs are computed based on the DIAs with probabilities and the DIAs without probabilities by algorithm in Fig. 3 separately. Next, the probabilities of the testing PPIs under the two strategies are compared according to the PCCs of them and GO similarities. Results of the comparisons are displayed in Table 8, where Prob_without means the probabilities of PPIs based on DIAs without probabilities; Prob_with means those based on DIAs with probabilities; “improvement” means improvements on PCCs of Prob_with against those of Prob_without. According to the results, the better inferences can be made based on the DIAs with probabilities than on those without probabilities. It may suggest that the probabilities of DIAs are beneficial for estimating probabilities of PPIs. It is also reflected that our strategy of measuring probabilities of DIAs is effective.
| Table 8 Compare PCCs of GO similarities and probabilities of the testing PPIs based on DIAs with and without probabilities |
4.5 Advantages of the Method
To test performance of our method, it is compared with the state-of-art methods of predicting PPIs based on domain-domain interactions. These methods include MSSC[26] and DCC[27]. The performance of these two methods and our method (RePIN) is evaluated on the testing PPIs too. Firstly, the three methods are trained on the testing PPIs to build models of predicting PPIs separately. And then, the models of the three methods are applied to predict the interactions between proteins of the testing PPIs. Their performance is shown in Table 9 and compared from two aspects: (1) the ability of finding PPIs; (2) the reliability of prediction. The ability of finding PPIs of a method is measured by the number of the testing PPIs which can be predicted by the method and represented by overlap in Table 9. The reliability of prediction of a method is evaluated by the PCCs of probabilities and GO similarities of PPIs predicted by the method, which can be calculated by formula (6) in section 4.2 and is represented by pcc in Table 9.
| Table 9 Compare performance of our method and the related methods |
According to the overlap, all of the three methods can detect above 80% testing PPIs and DCC detects the most testing PPIs among three methods.This suggests that DCC has better abilities to find PPIs than MSSC and RePIN.However, the reliability of DCC is clearly less than MSSC and RePIN according to the pcc.Among the three methods, RePIN has the best performance on the reliability of predicting PPIs. This may suggest that RePIN is more reliable on measuring probabilities of PPIs than the two methods.From Table 9, DCC can find more PPIs than others but these PPIs may include a high rate of spurious PPIs. Through further analysis, DCC predicts PPIs based on all DDIs and ignores that only DDIs across proteins can mediate interactions between proteins. So DCC may be misled by the DDIs within proteins and give misjudgment of PPIs. MSSC detects the majority of the testing PPIs but it shows lower PCCs of probabilities and GO similarities than RePIN. In MSSC, a set of DDIs are inferred based on a group of known positive PPIs and then PPIs are predicted based on these DDIs. The main idea is similar with our method, but they ignore the impact of the interacting biases of domains on PPIs, which limit its performance. On the whole, RePIN shows more favorable performances on predicting PPIs than others. The advantages of RePIN may attribute to: (1) Only DDIs across proteins are used to predict PPIs; (2) Interacting biases of domains are used to estimate probabilities of PPIs.
5 ConclusionsIn this paper, domain compositions of proteins are proven good clues to predict DDIs.Based on domain composition of the proteins in UniProt, 54519 DDIs are inferred by statistical significance tests. These DDIs are used to find potential PPIs in known PPI networks. However, many spurious PPIs are also brought into the network because the DDIs within proteins misled judgement on PPIs in the process. Specifically speaking, only DDIs across proteins can meditate PPIs and others within proteins cannot. Among the predicted DDIs, some DDIs exist within proteins while others exist across proteins.
To find DDIs across proteins, potential PPIs of the known network are detected based on the DDIs and then the potential PPIs are added into the original known network. After that, many domain pairs across proteins are constructed by combining domains of interacting proteins in the network. Next, a series of statistical significance tests are made on these pairs of domains to identify DDIs across proteins. Through experiments, this strategy is proved to be effective on finding DDIs across proteins. Although there are some spurious PPIs among the potential PPIs, the experimental results show that potential PPIs are useful supplement of the original network. This may also confirm that DDIs predicted from domain composition of proteins are beneficial for finding potential PPIs of the original network.
Additionally, it is found that interacting biases of domains have great impact on PPIs. In our method, interacting biases of domains are measured by combining conditional probabilities of the interacting domains. This strategy is also proved to be reasonable and effective by experiments.
Based on the above findings and strategies, a novel method for constructing PPI network is put forward. Our method is compared with the state-of-art methods of predicting PPIs including MSSC and DCC. They are used to predicting PPIs and the experimental results show that our method can provide more reliable judgments on PPIs than the two methods. Our method can be used to construct PPI network for new sequenced and well-studied organisms. It will promote the biological researches which depend on protein-protein interaction network.
| [1] |
Sharan R, Ulitsky I, Shamir R.Network-based prediction of protein function. Mol. Syst. Biol., 2007, 3:88.
( 0) 0)
|
| [2] |
Hu L, Huang T, Shi X, et al. Predicting functions of proteins in mouse based on weighted protein-protein interaction network and protein hybrid properties.
PLoS One, 2011 , 6 (1) .
( 0) 0)
|
| [3] |
Janga S C, Diaz-mejia J J, Moreno-hagelsieb G. Network-based function prediction and interactomics: the case for metabolic enzymes.
Metab. Eng, 2011 , 13 (1) : 1-10.
DOI:10.1016/j.ymben.2010.07.001 ( 0) 0)
|
| [4] |
Vijaykumar Yogesh M, Akash R. Evaluation of physical and functional protein-protein interaction prediction methods for detecting biological pathways.
PLoS One, 2013 , 8 (1) : 350-352.
( 0) 0)
|
| [5] |
Yeh C Y, Yeh H Y, Arias C R, et al. Pathway detection from protein interaction networks and Gene expression data using color-coding methods and A* search algorithms.
Scientific World Journal, 2012 , 2012 : 315797.
DOI:10.1100/2012/315797 ( 0) 0)
|
| [6] |
Tumuluru P, Ravi B, Ch S. A Survey on Identification of Protein Complexes in Protein-protein Interaction Data: Methods and Evaluation.
Springerbriefs in Applied Sciences & Technology, 2015 : 57-72.
( 0) 0)
|
| [7] |
Li X, Wu M, Kwoh C K, et al. Computational approaches for detecting protein complexes from protein interaction networks: a survey.
Bmc Genomics, 2010 , 11 (4) : 1-19.
DOI:10.1186/1471-2164-11-S1-S3 ( 0) 0)
|
| [8] |
Srihari S, Leong H W. A survey of computational methods for protein complex prediction from protein interaction networks.
Journal of Bioinformatics & Computational Biology, 2013 , 11 (2) : 50-55.
DOI:10.1142/S021972001230002X ( 0) 0)
|
| [9] |
Nepusz T, Yu H, Paccanaro A. Detecting overlapping protein complexes in protein-protein interaction networks.
Nat Methods, 2012 , 9 (5) : 471-472.
DOI:10.1038/nmeth.1938 ( 0) 0)
|
| [10] |
Li B-Q, Huang T, Liu L, et al. Identification of colorectal cancer related genes with mRMR and shortest path in protein-protein interaction network.
PLoS One, 2012 , 7 (4) : e33393.
DOI:10.1371/journal.pone.0033393 ( 0) 0)
|
| [11] |
Magger O, Waldman Y Y, Ruppin E, et al. Enhancing the prioritization of disease-causing genes through tissue specific protein interaction networks.
PLoS Comput Biol, 2012 , 8 (9) : e1002690-e1002690.
DOI:10.1371/journal.pcbi.1002690 ( 0) 0)
|
| [12] |
Deane C M, SalwiŃSki Ł, Xenarios I, et al. Protein interactions: two methods for assessment of the reliability of high throughput observations.
Molecular & Cellular Proteomics Mcp, 2002 , 1 (5) : 349-356.
( 0) 0)
|
| [13] |
Edwards A M, Bart K, Ronald J, et al. Bridging structural biology and genomics: assessing protein interaction data with known complexes.
Drug Discov Today, 2002 , 18 (10) : 529-536.
( 0) 0)
|
| [14] |
Mackay J P, Sunde M, Lowry J A, et al. Protein interactions: to believe or not to believe?.
Trends in Biochemical Sciences, 2008 , 33 (6) : 242-243.
DOI:10.1016/j.tibs.2008.04.003 ( 0) 0)
|
| [15] |
Von Mering C, Krause R, Snel B, et al. Comparative assessment of large-scale data sets of protein-protein interactions.
Nature, 2002 , 417 (6887) : 399-403.
( 0) 0)
|
| [16] |
Sprinzak E, Sattath S, Margalit H. How reliable are experimental protein-protein interaction data?.
J Mol Biol, 2003 , 327 (5) : 919-923.
DOI:10.1016/S0022-2836(03)00239-0 ( 0) 0)
|
| [17] |
Memišević V, Wallqvist A, Reifman J. Reconstituting protein interaction networks using parameter-dependent domain-domain interactions.
BMC Bioinformatics, 2013 , 14 (1) : 154.
DOI:10.1186/1471-2105-14-154 ( 0) 0)
|
| [18] |
Reimand J, Hui S, Jain S, et al. Domain-mediated protein interaction prediction: From genome to network.
Febs Letters, 2012 , 586 (17) : 2751-2763.
DOI:10.1016/j.febslet.2012.04.027 ( 0) 0)
|
| [19] |
Finn R D, Clements J, Eddy S R. HMMER web server: interactive sequence similarity searching.
Nucleic Acids Res, 2011 , 39 (8) : W29-W37.
DOI:10.1093/nar/gkr367 ( 0) 0)
|
| [20] |
Xenarios I, Salwinski L, Duan X J, et al. DIP, the Database of Interacting Proteins: a research tool for studying cellular networks of protein interactions.
Nucleic Acids Res, 2002 , 30 (1) : 303-305.
DOI:10.1093/nar/30.1.303 ( 0) 0)
|
| [21] |
Chatr-Aryamontri A, Breitkreutz B J, Oughtred R, et al. The BioGRID interaction database: 2015 update.
Nucleic Acids Res, 2015 , 43 (Database issue) : D470-D478.
DOI:10.1093/nar/gku1204 ( 0) 0)
|
| [22] |
Damian S, Andrea F, Stefan W, et al. STRING v10: protein-protein interaction networks, integrated over the tree of life.
Nucleic Acids Res, 2015 , 43 (Database issue) : :D447-D452.
DOI:10.1093/nar/gku1003 ( 0) 0)
|
| [23] |
Samuel K, Bruno A, Lionel B, et al. The IntAct molecular interaction database in 2012.
Nucleic Acids Res, 2012 , 40 (Database issue) : D841-D846.
DOI:10.1093/nar/gkr1088 ( 0) 0)
|
| [24] |
Zhang Q C, Petrey D, Deng L, et al. Structure-based prediction of protein-protein interactions on a genome-wide scale.
Nature, 2012 , 490 (7421) : 556-560.
DOI:10.1038/nature11503 ( 0) 0)
|
| [25] |
Zhang Q C, Petrey D, Garzon J I, et al. PrePPI: a structure-informed database of protein-protein interactions.
Nucleic Acids Res, 2013 , 41 (Database issue) : D828-D833.
DOI:10.1093/nar/gks1231 ( 0) 0)
|
| [26] |
Huang C B, Morcos F, Kanaan S P, et al. Predicting protein-protein interactions from protein domains using a set cover approach.
IEEE-Acm Transactions on Computational Biology and Bioinformatics, 2007 , 4 (1) : 78-87.
DOI:10.1109/TCBB.2007.1001 ( 0) 0)
|
| [27] |
Jang W H, Jung S H, Han D S. A computational model for predicting protein interactions based on multidomain collaboration.
IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), 2012 , 9 (4) : 1081-1090.
DOI:10.1109/TCBB.2012.55 ( 0) 0)
|
| [28] |
Priya S B, Saha S, Anishetty R, et al. A matrix based algorithm for protein-protein interaction prediction using domain-domain associations.
Journal of Theoretical Biology, 2013 , 326 : 36-42.
DOI:10.1016/j.jtbi.2013.02.016 ( 0) 0)
|
| [29] |
Marcotte E M, Pellegrini M, Ng H-L, et al. Detecting protein function and protein-protein interactions from genome sequences.
Science, 1999 , 285 (5428) : 751-753.
DOI:10.1126/science.285.5428.751 ( 0) 0)
|
| [30] |
Chia J M, Kolatkar P R. Implications for domain fusion protein-protein interactions based on structural information.
BMC Bioinformatics, 2004 , 5 (1) : 161.
DOI:10.1186/1471-2105-5-161 ( 0) 0)
|
| [31] |
Finn R D, Alex B, Jody C, et al. Pfam:the protein families database.
Nucleic Acids Res, 2014 , 42 (Database issue) : D222-D230.
( 0) 0)
|
| [32] |
Mosca R, Céol A, Stein A, et al. 3did:a catalog of domain-based interactions of known three-dimensional structure.
Nucleic Acids Res, 2014 , 42 (Database issue) : D374-D379.
DOI:10.1093/nar/gkt887 ( 0) 0)
|
| [33] |
Teng Z, Guo M, Liu X, et al. Measuring gene functional similarity based on group-wise comparison of GO terms.
Bioinformatics, 2013 , 29 (11) : 424-32.
DOI:10.1093/bioinformatics/btt160 ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23

