Self-localization technology is prerequisite to many functions of autonomous mobile robots (AMRs). There are generally two methods of indoor localization for robots:the Dead-Reckoning (DR) localization which utilizes the sensors independent of external information, such as odometers, digital compasses or inertial navigation sensors, and the beacon-based localization which requires sensors deployed over the whole positioning area [1-2].The DR is mainly flawed in two aspects:(1) it requires an absolute coordinate as starting point so that the later position can be conjectured by shifting the starting point along the relative translation vector; (2) cumulative error caused by wheel slippage, mechanical tolerances or sensor drift would severely corrupt the localization accuracy over a long travel. The beacon-based localization is usually realized through geometric operation on measures sampled from distributed beacons, especially the distance between receivers and transmitters. To obtain the distance measurements, the time of flight (TOF) is often adopted, given the transmission speed of the signal. It is the time that the signal takes to transfer from the transmitter to the receivers.
Several algorithms based on the least square principle have been proposed by scholars when more than three distance measurements are acquired concurrently by the source [3-7]. Chan [3]used a two-stage weighted least square (WLS) that applying the geometrical constraints of source and receivers on the solution of the nonlinear system of equation. Cheung [4] proposed a constrained weighted least squares (CWLS) mobile positioning approach that models uniformly beacon-based localization with different kinds of measurements. Kim [7] developed a localization system in which three passive sources were mounted on the AMR and made comparisons on the efficiency of several algorithms.
Combined the DR localization with beacon based localization, the real-time pose tracking of AMRs is possible even if distance measurements are partly or completely blocked sometimes. Extended Kalman filter (EKF) and interacting multiple model (IMM) are extensively used to fuse the results of the two localization approaches [8-18]. Usually, the EKF updates the pose of AMRs with translation and orientation increments, and corrects the a priori estimation with pose observation computed from distance measurements.Tsai [8] and Zhao[9] respectively derived a 3D post determination approach based on EKF, using multi-sensorial INS system which includes gyroscopes, accelerometers, encoders and digital compasses.Kim[13] specially compared the positioning accuracy of loosely coupled observation and tightly coupled observation in correcting the a priori pose estimation.
However, all approaches mentioned above require at least three distance measurements obtained concurrently for 2D localization. Thus, numerous sensor beacons need to be deployed all over the area where localization is executed. High density of beacons results in a considerable cost of building such a sensor network. In some cases where neither high positioning accuracy is required nor the accumulation error is allowed, the localization approach uses the least number of sensor beacons would be every useful. For example, in places like a huge library or an airport, we only need to know the rough location of the source, either an AMR or a human being wearing the localization devices. On one hand, the positioning accuracy would not deteriorate unboundedly over long travel due to the localization beacons. On the other hand, it would be very economical to cover as large area as possible with few beacons.
This paper proposes alocalization approach that uses only the sequential time of flight (STOF) measurements from a single beacon. The STOF is a series of TOF measurements that are acquired by the source in sequence. The utilization of STOF makes it unnecessary to obtain at least three distances to localize. A double-layer Kalman filter (DLKF), which is a variation of the EKF, is developed both to obtain the relative translation vector essential to the STOF localization and to fuse the results of STOF localization with the DR method. On the basis of STOF localization, localization can be fulfilled without having to overlapping coverage area of beacons. Therefore, a place can be covered by the least possible number of beacons, which reduces remarkably the cost of installation of such a localization system.
2 Mathematical Model of STOF LocalizationLet [x, y, z]T be the coordinate of the AMR referred from the receiver coordinate frame O, whose coordinate is [X, Y, Z] referred from the global coordinate frame O0. When the AMR is moving in indoor environment, we believe the height of the source is a constant h. Thus, the 3D localization degrades to a plenary localization and, from now on, we would only concern s=[x, y]T. Let dk be the projection of dkr, the real distance between the source and the beacon, onto the plane where the AMR is in at moment k.Given Z, the height of the AMR and the real distance dkr, dk can always be derived using the relationship
| $ d_k^2 + {\left( {Z - h} \right)^2} = d_{kt}^2 $ | (1) |
We use dk in the rest of the paper instead of denoting explicitly the real distance with dkt for sake of computational simplicity. Considering two moments k-1 and k when the AMR is at different positions whose coordinate is Pi(xi, yi) (i=k-1, k), referred from the receiver coordinate system, and the corresponding distance measurements are dk-1, dk.
From Fig. 1, we get a system of equations
| $ \left\{ {\begin{array}{*{20}{l}} {d_{k - 1}^2 = {{\left( {{x_k} - \Delta {x_k}} \right)}^2} + {{\left( {{y_k} - \Delta {y_k}} \right)}^2}}\\ {d_k^2 = {x_k}^2 + {y_k}^2} \end{array}} \right. $ | (2) |
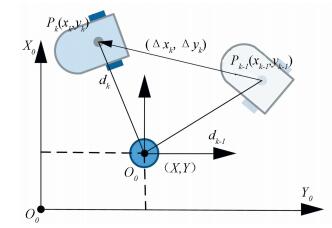
|
Figure 1 Schematic of STOF localization |
where Δxk, Δyk is the relative translation from Pk-1 to Pk. Immediately solve the system of equations and solve yk in term of xk, we have
| $ {y_{k - 1}} = \frac{{\left( {d_k^2 - d_{k - 1}^2 + \Delta x_k^2 + \Delta y_k^2} \right) - 2\Delta {x_k}{x_{k - 1}}}}{{2\Delta {y_k}}} $ | (3) |
As Eq.(3) infers, if AMRs happen to move along X axis, the analytical solution of yk is rendered meaningless, and in a similar way the analytical solution of xk becomes meaningless if xk is solved in term of yk and AMRs move along Y axis. Even if the track of AMRs is not strictly parallel to the coordinate axis, the error contained in numerator would corrupt positioning accuracy severely due to the amplification effect of denominator.
Therefore, instead of using the analytical solution, we use Newton iteration to get a numerical solution of the system of equation by applying iteratively the following equation
| $ \boldsymbol{s}_k^* = \boldsymbol{s}_k^* - \boldsymbol{F} \cdot \boldsymbol{F}{'^{ - 1}} $ | (4) |
where
| $ \boldsymbol{s}_k^* = {\left[ {{x_k},{y_k}} \right]^{\rm{T}}} $ |
| $ \begin{array}{l} \boldsymbol{F} = \left[ {\begin{array}{*{20}{c}} {{{\left( {{x_k} - \Delta {x_k}} \right)}^2} + {{\left( {{y_k} - \Delta {y_k}} \right)}^2} - d_{k - 1}^2}\\ {x_k^2 + y_k^2 - d_k^2} \end{array}} \right]\\ \boldsymbol{F}' = \frac{{\partial \boldsymbol{F}}}{{\partial \left( {x,y} \right)}} = 2\left[ {\begin{array}{*{20}{c}} {{x_{k - 1}} - \Delta {x_k}}&{{y_{k - 1}} - \Delta {y_k}}\\ {{x_k}}&{{y_{k - 1}}} \end{array}} \right] \end{array} $ |
The convergence condition of Eq. (4) is that as long as AMRs are not moving along the radius of the origin of the receiver coordinate frame O, namely |F|≠0, the sk* converges within 10 rounds of iteration, given an initial value s0 suitably close to the real value s. The coordinate of AMRs referred from the global coordinate frame is hence given by
| $ {\boldsymbol{s}_k} = \boldsymbol{s}_k^* + {\left[ {X,Y} \right]^{\rm{T}}} $ |
In the case when the track of AMRs is close to the radius of O, the result needs to be handled particularly, which will be discussed in the next section.
3 Error Analysis of STOFIn the STOF localization model, the localization result is corrupted by two kinds of errors:the error of relative translation and the error of distance measurements.The total error is linear combination of different error items.By the error propagation rule, we have
| $ {{\boldsymbol{\hat \delta} }_k} = \left[ {\begin{array}{*{20}{c}} {\delta {x_k}}\\ {\delta {y_k}} \end{array}} \right] = \frac{{\partial {\boldsymbol{s}_k}}}{{\partial \left( {{d_{k - 1}},{d_k},\Delta {x_k},\Delta {y_k}} \right)}}{\boldsymbol{\varepsilon} ^{\rm{T}}} = \boldsymbol{F}{'^{ - 1}}\boldsymbol{G}{\boldsymbol{\varepsilon} ^{\rm{T}}} $ | (5) |
where
| $ \begin{array}{l} \boldsymbol{G} = 2\left[ {\begin{array}{*{20}{l}} {{d_{k - 1}}}&{{x_k} - \Delta {x_k}}&{{y_k} - \Delta {y_k}}\\ 0&{{d_k}}&0&0 \end{array}} \right]\\ \;\;\;\;\;\;\;\varepsilon = \left[ {{\varepsilon _{{d_{k - 1}}}},{\varepsilon _{{d_k}}},{\varepsilon _{\Delta {x_k}}},{\varepsilon _{\Delta {y_k}}}} \right] \end{array} $ |
where εdk-1, εdk, εΔxk, εΔykrespectively represent the error of dk-1, dk, Δxk, Δyk. The error expression also indicates that when F is close to a singular matrix, the positioning error would approximate infinite. Fig. 2(a) shows an instance of the condition number F’ plotted against θ and its corresponding error estimation result, wherein

|
Figure 2 Error analysis of STOF with regard to direction angle of translation vector |

|
Figure 3 Schematic of relative translation extraction failure |
Fig. 2 presents the plot of the difference between the true error and the estimated error against θ when Eq. (5) is used to estimate the positioning error, solid line being |δxk-
DR method can be adopted to obtain the relative translation vector [Δxk, Δyk]. Usually, the error of unit travel is white Gaussian and the variance of the length of the relative translation vector is proportionate to the distance travelled [19]. On the other hand, the error of the distance measures εdk is usually white Gaussian noise with variance σs2. Therefore, the covariance matrix of localization error can be estimated with the following equation if the localization result is not discarded.
| $\boldsymbol{\psi} = \boldsymbol{E}\left( {{\boldsymbol{\hat \delta }_\boldsymbol{k}}\boldsymbol{\hat \delta }_\boldsymbol{k}^\boldsymbol{T}} \right) = \boldsymbol{F}{'^{ - 1}}\boldsymbol{G}\boldsymbol{\mathit{\Phi}} {\boldsymbol{G}^\boldsymbol{T}}{\left( {\boldsymbol{F}{'^{ - 1}}} \right)^{\rm{T}}}$ | (6) |
where
| $ \begin{array}{l} \boldsymbol{\mathit{\Phi}} = {\rm{diag}}\left[ {\sigma _s^2,\sigma _s^2,\sigma _d^2{{\cos }^2}\theta ,\sigma _d^2{{\sin }^2}\theta } \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta = \Delta {y_k}/\Delta {x_k} \end{array} $ |
Therefore, the result of STOF localization rk, which contains noise
The two layers of the DLKF are the bottom layer (BL), which is used to extract the relative translation, and the top layer (TL), which calculates the real-time coordinate of AMRs.
The system of BL is given by the following equations:
| $ \begin{array}{l} {\boldsymbol{r}_{b|k}} = f\left( {{\boldsymbol{r}_{b|k - 1}},{\boldsymbol{u}_{b|k}},{\boldsymbol{\omega} _{b|k}}} \right) = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{x_{b|k}} + \Delta {d_k}\cos \left( {{\theta _k} + \Delta {\theta _k}/2} \right) + {\omega _{b|k1}}}\\ {{y_{b|k}} + \Delta {d_k}\sin \left( {{\theta _k} + \Delta {\theta _k}/2} \right) + {\omega _{b|k2}}}\\ {{\theta _{b|k}} + \Delta {\theta _k} + {\omega _{b|k3}}} \end{array}} \right] \end{array} $ | (7) |
| $ {z_{b|k}} = {\boldsymbol{H}_b}{\boldsymbol{r}_{b|k}} + {\boldsymbol{v}_k} $ | (8) |
where subscript k is the discrete time index of BL; rb=[xb, yb, θ]T is the state space of BL; xb, yb being referred from the AMR’s own coordinate system; Δdk, Δθk are distance increment and angle increment; ub is the control input of the BL; ωb is white Gaussian noise vector and E(ωb ωTb)=Q; z is the orientation measurement; Hb=[0, 0, 1], E(vkvkT)=R.
An Extended Kalman Filter is applied to the system of the BL:
| $ \boldsymbol{\hat r}_{b|k}^ - = f\left( {\boldsymbol{\hat r}_{b|k - 1}^ + ,{\boldsymbol{u}_{b|k}},0} \right) $ | (9) |
| $ \boldsymbol{P}_{b|k}^ - = \boldsymbol{AP}_{b|k - 1}^ + {\boldsymbol{A}^{\rm{T}}} + \boldsymbol{Q} $ | (10) |
| $ {\boldsymbol{K}_{b|k}} = \boldsymbol{P}_{b|k}^ - \boldsymbol{H}_b^{\rm{T}}{\left( {{\boldsymbol{H}_b}P_{b|k}^ - \boldsymbol{H}_b^{\rm{T}} + R} \right)^{ - 1}} $ | (11) |
| $ \boldsymbol{\hat r}_{b|k}^ - = \boldsymbol{\hat r}_{b|k}^ - + {\boldsymbol{K}_{b|k}}\left( {{z_{b|k}} - \boldsymbol{H}\boldsymbol{\hat r}_{b|k}^ - } \right) $ | (12) |
| $ \boldsymbol{P}_{b|k}^ + {\rm{ = }}\left( {\boldsymbol{1}{\rm{ - }}{\boldsymbol{K}_{b|k}}{\boldsymbol{H}_b}} \right)\boldsymbol{P}_{b|k}^ + $ | (13) |
where Pb is the covariance matrix of the BL; Kb is the Kalman gain of the BL; A is the state transition matrix given by
| $ \boldsymbol{A} = \frac{{\partial f\left( {\boldsymbol{\hat r}_{b|k - 1}^ + ,{\boldsymbol{u}_{b|k}},0} \right)}}{{\partial {\boldsymbol{r}_{b|k - 1}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&{ - \Delta {d_k}\sin \left( {{\theta _k} + \Delta {\theta _k}/2} \right)}\\ 0&1&{\Delta {d_k}\cos \left( {{\theta _k} + \Delta {\theta _k}/2} \right)}\\ 0&0&1 \end{array}} \right] $ |
The system of TL is given by
| $ {\boldsymbol{r}_{t|n}} = {\boldsymbol{r}_{t|n - 1}} + {\boldsymbol{u}_{t|n}} + {\boldsymbol{\omega} _{t|n}} $ | (14) |
| $ {\boldsymbol{z}_{t|n}} = {\boldsymbol{H}_t}{\boldsymbol{r}_{t|n - 1}} + {\boldsymbol{v}_{t|n}} $ | (15) |
where subscript n is the discrete time index of the TL; rt=[xt, yt]Tis the state space of the TL, xt, yt being referred from the beacon coordinate system; ut is the control input of the TL, which is also the translation of the AMR within a time step of the TL; Ht=I2×2; ωt is white Gaussian noise vector of control input and E(ωtωtT)=k2Q, k being a factor determined by the ratio of the TL’s time step to the BL’s time step; yt is the observation obtained by STOF localization with the noise vector vt whose covariance matrix can be estimated by Eq. (6).
A Kalman Filter is applied to the system of TL:
| $ \boldsymbol{\hat r}_{t|n}^ - = \boldsymbol{\hat r}_{t|n - 1}^ + + {\boldsymbol{u}_{t|n}} $ | (16) |
| $ \boldsymbol{P}_{t|n}^ - = \boldsymbol{P}_{t|n - 1}^ + + {k^2}\boldsymbol{Q} $ | (17) |
if Dn≤Dthreshold
| $ {\boldsymbol{K}_{t|n}} = \boldsymbol{P}_{t|n}^ - \boldsymbol{H}_{\rm{t}}^{\rm{T}}{\left( {{\boldsymbol{H}_t}P_{t|n}^ - \boldsymbol{H}_t^{\rm{T}} + {\psi _n}} \right)^{ - 1}} $ | (18) |
| $ \boldsymbol{\hat r}_{t|n}^ + = \boldsymbol{\hat r}_{t|n}^ - + {\boldsymbol{K}_{t|n}}\left( {{\boldsymbol{z}_{t|n}} - \boldsymbol{\hat r}_{t|n}^ - } \right) $ | (19) |
| $ \boldsymbol{P}_{t|n}^ + = \left( {{\boldsymbol{I}_{2 \times 2}} - {\boldsymbol{K}_{t|n}}{\boldsymbol{H}_t}} \right)\boldsymbol{P}_{t|n}^ + $ | (20) |
else
discard yn,
| $ \begin{array}{l} \boldsymbol{\hat r}_{t|n}^ + = \boldsymbol{\hat r}_{t|n}^ - \\ \boldsymbol{P}_{t|n}^ + = \boldsymbol{P}_{t|n}^ - \end{array} $ |
where Pt is the covariance matrix of the TL; Kt is the Kalman gain of the TL. Dn=‖yn-
Assuming that the time steplength of the BL is τ and the time step length of the TL is T. They are both determined by the sample period of the sensors employed and we assume T=cτ(c≥1∪c∈Z). Therefore, the relationship between n and k is expressed by k=cn. The BL and the TL proceed separately and communicate from time to time in the following manner:
(1)Upon initialization, rb|0 is given an arbitrary value since we are only interested in the relative translation in the BL.θ0 will be corrected later by the orientation sensor.
(2)Every time the BL is updated, store the current coordinate record (xb|k, yb|k) along with the translation ub|k in the memory.
(3) The TL starts iteration only after a buffer that has c×N cells is filled with the coordinate records of BL for the first time.
(4)The TL is updated once within T while BL is updated c times. The control input of the TL ut|nis given by
| $ {\boldsymbol{u}_{t|n}} = {\left[ {{x_{b|k}},{y_{b|k}}} \right]^{\rm{T}}} - {\left[ {{x_{b|k - c}},{y_{b|k - c}}} \right]^{\rm{T}}} $ | (21) |
(5) The relative translation vector needed by the STOF localization is obtained via
| $ \begin{array}{l} \Delta {x_{t|n}} = {x_{b|cn}} - {x_{b|c\left( {n - N} \right)}}\\ \Delta {y_{t|n}} = {y_{b|cn}} - {y_{b|c\left( {n - N} \right)}} \end{array} $ | (22) |
where N is the time interval between two records of the BL.N determines the length of the relative translation vector on most occasions. Note from Eq. (5) that the length of the relative translation vector cannot be arbitrarily decreased, otherwise, the condition number of F would become very large;
The reasons why we introduce the DLKF lie in that:
1) It effectively organizes the data fusion especially when a considerable difference between the sample rates of distinct type of sensors exists. For example, more often than not, ultrasonic sensors have a sample period larger than that of odometers, considering a roughly 340 m/s propagation velocity of ultrasonic in air.
2) It avoids the potential extraction failure of relative translation due to a huge correction of the AMR’s absolute coordinate, which is illustrated in Fig. 3.
In Fig. 3, rb is the records of the coordinate of the AMR in the BL, referred from its own coordinate system; rt is the records in the TL, referred from the beacon coordinate system. The true relative translation vector is
| $ \left[ {\Delta x,\Delta y} \right] = r_t^* - {r_t} = r_b^* - {r_b} $ |
Thus, we need only to know two records referred from the coordinate system to extract the correct relative translation vector. If the relative translation vector extraction is, however, implemented in a single layer, an extraction failurecan occur because the AMR would mistakenly obtain a relative translation vector via operating subtraction on two records referred from different coordinate system.
5 Simulation ExperimentA real-scenario computer simulationusing Matlab is conducted to validate STOF localization. Ultrasonic sensors are widely used in measuring the distance. The time synchronization can be attained by using RF transmitters so that the TOF can be accurately measured [20].The standard deviation of ultrasonic sensors can be as small as 0.22 cm when measuring a range of about 1 m [13].When using as the orientation sensor, digital compasses have white Gaussian noise εc of which variance σc2 is about 4×10-4 rad2. For the detailed description of realization of the TOF measurements and localization system, please refer to the corresponding literature; we are not going to elaborate on it here. The simulation model and the physical configuration are illustrated in Fig. 4.
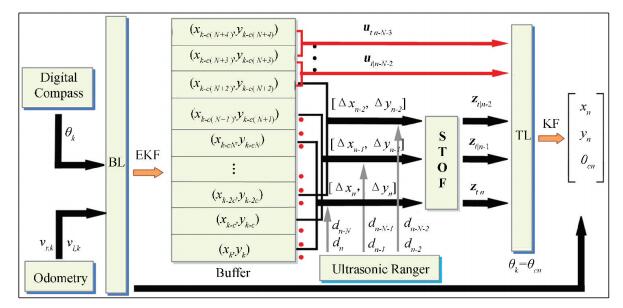
|
Figure 4 Simulation model and hardware configuration |
The state input of BL is
| $ \Delta {d_k} = \left( {{v_{r,k}} + {v_{l,k}}} \right)\tau /2,\Delta {\theta _k} = \left( {{v_{r,k}} - {v_{l,k}}} \right)\tau /b $ |
where vr, k, vl, kare the speed measurement of the right wheel and the left wheel. As the beginning of the DLKF, the BL is initialized as
| $ \boldsymbol{\hat r}_{b|0}^ + = {\left[ {0,0,0} \right]^{\rm{T}}},\boldsymbol{\hat P}_{b|0}^ + = {\rm{diag}}\left[ {0,0,4{{\rm{\pi }}^2}} \right] $ |
The TL is initialized as
| $ \boldsymbol{\hat r}_{t|0}^ + {\rm{ = }}{\left[ {0,0} \right]^{\rm{T}}},\boldsymbol{\hat P}_{{\rm{t}}|0}^ + = {\rm{diag}}\left[ {\infty ,\infty } \right] $ |
The rest of parameters of the simulation are listed in Table 1 and the corresponding figure caption. The STOF localization simulated in the program is not strictly controlled to use any data related to the true track. So the position estimation is completely based DR method and STOF localization.
| Table 1 Parameters of Matlab simulation |
The simulations of different tracks of the AMR are displayed in Figs. 5 and 6.
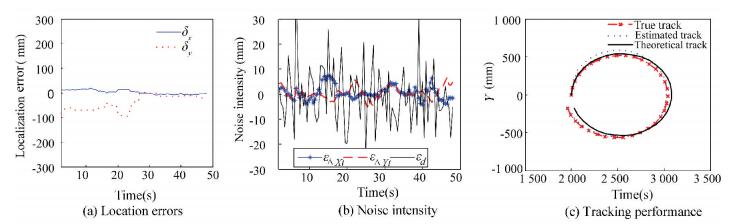
|
Figure 5 Simulation result (vr=50 mm/s, vl=80 mm/s, N=5, σs2=114.8 mm2, σd2=47 mm2/s2, σc2=9.8e-4 rad2) |

|
Figure 6 Simulation result (vr=50 mm/s, vl=50 mm/s, N=5, σs2=101.4 mm2, σd2=437 mm2/s2, σc2=9.3e-4 rad2) |
In Figs. 5(c) and 6(c), solid line is plotted with original measurements of odometer only, which is the theoretical track that the AMR “thought” it would have. The dash line is the true track of the AMR, which deviates from the theoretical track a while after the AMR launched. The blue dash line is the estimated track of the AMR using the STOF localization results as observations. As the iteration of the DLKF proceeding, the positioning error decreases and finally remains stably near zero line with little fluctuation due to both the error of relative translation vector εΔxtεΔyt and the error of distance measure εdt-1εdt, which is shown in Figs. 5(b) and 6(b). In Fig. 5, the generated noise is about 10 times of that in Fig. 6. As indicated by the localization error plot, the initial positioning error and the transition time, the time that the DLKF takes to reach a high positioning accuracy, of Fig. 5 is thus far less than those of Fig. 6. On the other hand, the positioning error of both simulations converging to a small domain of zero over time also indicates that the STOF localization scheme has a strong immunity against the noise.
Fig. 7 presents another group of simulations.All simulations in the group share exact the same noise through the whole process. The only difference is the value of N, varying from 5 to 30.It is very clear that both the initial estimation error and the transition time decrease as N increases. However, a greater N means a later estimation starting time and a larger buffer to store intermediate records of the BL because an N-cell buffer needs to be filled for the first time before the TL can start iteration.

|
Figure 7 Simulation result when N=5, 10, 20, 30 |
6 Conclusion
This paper proposes a new way of localization for AMRs called the STOF localization, which utilizes the displacement measurements from the DR method and distance measurements from a beacon. The proposed DLKF functions efficiently in fusing the several results of the STOF localization. Note that the sensors employed in the simulation of this paper are not the only options. STOF estimation can be applied to the other localization schemes which use different sensors and thus are of great value in practice.
| [1] |
Borenstein J, Everett H R, Feng L, et al. Mobile robot positioning: Sensors and techniques.
Journal of Robotic Systems, 1997 , 14 (4) : 231-249.
DOI:10.1002/(ISSN)1097-4563 ( 0) 0)
|
| [2] |
Wu Chia-Ju, Tsai C C. Localization of an autonomous mobile robot based on ultrasonic sensory information.
Journal of Intelligent and Robotic Systems, 2001 , 30 (3) : 267-277.
DOI:10.1023/A:1008154910876 ( 0) 0)
|
| [3] |
Chan Y T, Ho K C. A simple and efficient estimator for hyperbolic location.
IEEE Transactions on Signal Processing, 1994 , 42 (8) : 1905-1915.
DOI:10.1109/78.301830 ( 0) 0)
|
| [4] |
Cheung K W, So H C, Ma W K. A constrained least square approach to mobile positioning: Algorithms and optimality.
Eurasip Journal on Applied Signal Processing, 2006 , 2006 (1) : 1-23.
DOI:10.1155/ASP/2006/20858 ( 0) 0)
|
| [5] |
Yu Huagang, Huang Gaoming, Gao Jun, et al. An efficient constrained weighted least squares algorithm for moving source location using TDOA and FDOA measurements.
IEEE Transactions on Wireless Communications, 2012 , 11 (1) : 44-47.
DOI:10.1109/TWC.2011.102611.110728 ( 0) 0)
|
| [6] |
Yang Kai, An Jianping, Bu Xiangyuan, et al. Constrained total least-squares location algorithm using time-difference-of-arrival measurements.
IEEE Transactions on Vehicular Technology, 2010 , 59 (3) : 1558-1562.
DOI:10.1109/TVT.2009.2037509 ( 0) 0)
|
| [7] |
Kim Seong Jin, Kim Byung Kook. Accurate hybrid global self-localization algorithm for indoor mobile robots with two-dimensional isotropic ultrasonic Receivers.
IEEE Transactions on Instrumentation and Measurement, 2011 , 60 (10) : 3391-3404.
DOI:10.1109/TIM.2011.2126890 ( 0) 0)
|
| [8] |
Tsai C C, Lin H H, Lai S W. Multisensor 3D posture determination of a mobile robot using inertial and ultrasonic sensors.
Journal of Intelligent and Robotic Systems, 2005 , 42 (4) : 317-335.
DOI:10.1007/s10846-005-3894-1 ( 0) 0)
|
| [9] |
Zhao He, Wang Zheyao. Motion measurement using inertial sensors, ultrasonic sensors, and magnetometers with extended Kalman filter for data fusion.
IEEE Sensors Journal, 2012 , 12 (5) : 943-953.
DOI:10.1109/JSEN.2011.2166066 ( 0) 0)
|
| [10] |
Lindsay Kleeman. Optimal estimation of position and heading for mobile robots using ultrasonic beacons and dead-reckoning.
IEEE International Conference on Robotics and Automation, 1992 , 3 : 2582-2587.
DOI:10.1109/ROBOT.1992.220053 ( 0) 0)
|
| [11] |
Tsai C C. An accurate localization for mobile robot using extended Kalman filter and sensor fusion.
IEEE Transactions on Instrumentation and Measurement, 1998 , 47 (5) : 1399-1404.
DOI:10.1109/IJCNN.2008.4634210 ( 0) 0)
|
| [12] |
Lin H H, Tsai C C. Ultrasonic localization and pose tracking of an autonomous mobile robot via fuzzy adaptive extended information filtering.
IEEE Transaction on Instrumentation and Measurement, 2008 , 57 (9) : 2024-2034.
DOI:10.1109/TIM.2008.919020 ( 0) 0)
|
| [13] |
Kim Su Yong, Yoon Kang Sup. The localization of a mobile robot using a pseudolite ultrasonic system and a dead reckoning integrated system.
International Journal of Control, Automation and Systems, 2011 , 9 (2) : 339-347.
DOI:10.1007/s12555-011-0216-1 ( 0) 0)
|
| [14] |
Zhang Yunzhou, Wu Chengdong, Cheng Long, et al. Localization and tracking of indoor mobile robot with ultrasonic and dead-reckoning sensors.
Journal of Computational Information Systems, 2012 , 8 (2) : 531-539.
( 0) 0)
|
| [15] |
Blom Henk A P, Bar-Shalom Y. The interacting multiple model algorithm for systems with Markovian switching coefficients.
IEEE Transactions on Automatic Control, 1988 , 33 (8) : 780-783.
DOI:10.1109/9.1299 ( 0) 0)
|
| [16] |
Kirubarajan T, Bar-Shalom Y. Kalman filter versus IMM estimator: When do we need the latter.
IEEE Transactions on Aerospace and Electronic Systems, 2003 , 39 (4) : 1453-1456.
DOI:10.1117/12.392013 ( 0) 0)
|
| [17] |
Song H Y. Mobile node localization using fusion prediction-based interacting multiple model in cricket sensor network.
IEEE Transactions on Industrial Electronics, 2012 , 59 (11) : 4349-4359.
DOI:10.1109/TIE.2011.2151821 ( 0) 0)
|
| [18] |
Dan Simon. Optimal State Estimation: Kalman, H∞ and Nonlinear Approaches. Hoboken, NJ: Wiley, 2006.
( 0) 0)
|
| [19] |
Chong K S, Kleeman L. Accurate odometry and error modeling for a mobile robot.
IEEE International Conference on Robotics and Automation, 1997 , 4 : 2783-2788.
DOI:10.1109/ROBOT.1997.606708 ( 0) 0)
|
| [20] |
Sanchez A, de Castro A, Elvira S. Autonomous indoor ultrasonic positioning system based on a low-cost conditioning circuit.
Measurement, 2011 , 45 (3) : 276-283.
DOI:10.1016/j.measurement.2011.12.002 ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


