2. School of Material Science and Engineering, Hebei University of Technology, Tianjin 300130, China
Since Onsager[1] gave the exact solution of 2-dimensional Ising model, 3-dimensional Ising model has attracted the attention of many researchers[2-6], because the Onsager solution can explain the phase-transfer phenomenon. There are various techniques to investigate 3-dimensional Ising model: the renormalization group technique[7], cluster variational method[8], linear chain approximation[9], molecular field approximation[10], etc. Liu et al. [11] have discussed nonlinear magnetization dynamics of a classical ferromagnet with anisotropies in an external magnetic field. Jiang et al. [12] have examined the phase diagrams of a single spin-1 Ising system and given the general expressions of the second-order phase transition. Recently, El-Showk et al. [13] have tried to use the constraints of crossing symmetry and unitarity in general 3D conformal field theories to solve 3-dimension Ising model. They found that 3-dimensional Ising model lies at a corner point on the boundary of the allowed parameter space which makes it difficult to be solved. Jin et al. [14] studied the phase transition of Ising model by using Monte Carlo simulations. Wu et al. [15] used the bond-propagation algorithm to study the finite-size Ising model. They found that boundary conditions have remarkable effects on the free energy and specific heat. Deviren et al. [16] have studied Ising model in a time-dependent external magnetic field by using effective-field theory. They identified the phase transition point as the minimum-correlation point and studied the critical condition of the system. Heyl et al. [17] have shown that 3D Ising model generates periodic nonanalytic behavior during phase transition. Campo et al. [18] used the method of controlling asymptotic parameter to study phase transition of Ising model. Ates et al. [19] identified a first-order dynamical phase transition of 3D Ising model and studied the behavior of thermal parameters during phase transition. Zhang et al.[20] used Ising model to explain the frustration in magnetic systems. Barnett et al. [21] compared the long-range interaction and shor-range interaction of Ising model near critical point. Schoelz et al. [22] used Ising model to investigate the graphene system and studied the changing of thermal parameters during phase transition. Dublenych[23] found a complete and exact solution of the ground-state problem for the Ising model on the Shastry-Sutherland lattice in an applied magnetic field. Lau et al. [24] used numerical calculation to study the thermal parameters for Ising model. They used a bond propagation algorithm and calculate the change of entropy during phase transition. Langer[25] used numerical simulations to study the correlation lengths of Ising model at critical points. Fytas et al. [26] solved the partition function of Ising model by performing statistics simulation. They found that specific heat rise exponentially near the critical point. Wu et al. [27] used the bond-propagation algorithm to calculate a rectangle Ising model. They have determined the exact expansions of the critical free energy and specific heat. Corberi et al. [28] studied the nonconserved phase-ordering dynamics of random-field Ising model. They confirmed the crossover to an asymptotic logarithmic behavior of thermal parameters during phase transition. Powalski et al. [29] investigated the transverse field Ising model on a triangular lattice and discovered a second-order quantum phase transition in the high-field limit. Damski[30] derived an exact closed-form expression for fidelity susceptibility of the quantum Ising model. Bastidas et al. [31] established a set of nonequilibrium phase transitions in the Ising model. They showed that the system exhibits and anisotropic transition. Henry et al. [32] studied the ground-state properties of Ising model by using spin-wave theory. They found that the ground-state system becomes stable in zero field. Jin et al. [33] investigated the thermal phase transition of a square-lattice Ising model. They discovered that the system is stabilized below a critical temperature.
Many theoretical works have been studied by the effective-field theory with correlations, but the core of Ising model is to obtain the largest eigenvalue of the transfer matrix and there is lack of understanding of the mathematical structure of the transfer matrix.
In this paper, we study the eigenvalues of the 3-dimensional Ising model of N1×N2×N3. In Section 2, we build a 2N1N2×2N1N2 transfer matrix V1, and then we build a much smaller matrix V2 which contains some eigenvalues including the largest eigenvalue λmax of V1. If N3 is infinite, we only need to obtain the largest eigenvalue of V1.But in this paper, we set N1 and N2 at finite values.N1 and N2 are the finite width of our model. Then we use λmax to calculate the specific heat per atom Cpa and the magnetic momentum per atom Mpa in Section 3.In Section 4, the important conclusions are drawn.
2 Basic ModelThe 3-dimensional Ising model is a cubic lattice of N1×N2×N3 sites. These sites are occupied by atoms with positive or negative spin. We use σj, k, l=±1 to represent the spin sign of atoms. The total energy of the lattice is:
| $\begin{gathered} E = \sum\limits_{j = 0}^{{N_1} - 1} {\sum\limits_{h = 0}^{{N_2} - 1} {\sum\limits_{l = 0}^{{N_3} - 1} {\left( { - {J_1}{\sigma _{j,h,l}}{\sigma _{j + 1,h,l}} - } \right.} } } \\ \left. {{J_2}{\sigma _{j,h,l}}{\sigma _{j,h + 1,l}} - {J_3}{\sigma _{j,h,l}}{\sigma _{j,h,l + 1}} - \mu B{\sigma _{j,h,l}}} \right) \\ \end{gathered} $ | (1) |
where J1, J2, J3 are the interaction energy between neighbors; μ is the spin magnetic moment; B is the magnetic field. The boundary condition is σ0, h, l=σN1, h, l, σj, 0, l=σj, N2, l, σj, h, 0=σj, h, N3.
The partition function is:
| $Z = \sum\limits_{{\sigma _{j,h,l}} = \pm 1} {{e^{ - \frac{E}{{kT}}}}} $ | (2) |
The free energy F can be derived from Z. The specific heat C, the magnetic moment M can be derived from F:
| $F = - kT\ln Z$ | (3) |
| $C = - T\frac{{{\partial ^2}F}}{{\partial {T^2}}}$ | (4) |
| $M = - \frac{{\partial F}}{{\partial B}}$ | (5) |
To calculate Z, we divide the lattice into N3 layers. Each layer contains N1 rows and N2 sites per row. We use a number νl to represent the state of the lth layer, 1≤νl≤2N1N2. The total energy of the lattice can be written as:
| $E = \sum\limits_{l = 0}^{{N_3} - 1} {{E_1}\left( {{v_1}} \right) + \sum\limits_{l = 0}^{{N_3} - 1} {{E_2}\left( {{v_l},{v_{l + 1}}} \right)} } $ | (6) |
| $\begin{gathered} {E_1}\left( {{v_l}} \right) = \sum\limits_{j = 0}^{{N_1} - 1} {\sum\limits_{h = 0}^{{N_2} - 1} {\left( { - {J_1}{\sigma _{j,h,l}}{\sigma _{j + 1,h,l}} - } \right.} } \hfill \\ {J_2}{\sigma _{j,h,l}}{\sigma _{j,h + 1,l}} - \mu B{\sigma _{j,h,l}} \hfill \\ \end{gathered} $ | (7) |
| ${E_2}\left( {{v_l},{v_{l + 1}}} \right) = \sum\limits_{j = 0}^{{N_1} - 1} {\sum\limits_{h = 0}^{{N_2} - 1} {{J_3}{\sigma _{j,h,l}}{\sigma _{j,h,l + 1}}} } $ | (8) |
Then the partition function turns into:
| $Z = \sum\limits_{{v_l}} {\prod\limits_{l = 0}^{{N_3} - 1} {{e^{ - {E_1}\left( {{v_l}} \right) - {E_2}\left( {{v_l},{v_{l + 1}}} \right)}}} } $ | (9) |
where
| $Z = Tr\left( {V_1^{{N_3}}} \right) = \lambda _1^{{N_3}} + \lambda _2^{{N_3}} + \lambda _3^{{N_3}} + \ldots $ | (10) |
where λ1, λ2, λ3, ... are the different eigenvalues of V1. Assuming λ1 is the largest eigenvalue λmax, if N3 is infinite, then:
| $\mathop {\lim }\limits_{{N_3} \to \infty } \left( {\lambda _1^{{N_3}} + \lambda _2^{{N_3}} + \lambda _3^{{N_3}} + \ldots } \right) = \lambda _1^{{N_3}}$ | (11) |
Now we only need to obtain the largest eigenvalue λmax of matrix V1 and Z=λmaxN3.
We will use a special case to explain how to obtain λmax. When N1=2, N2=1, V1 can be expressed as:
| $\begin{array}{l} {V_1} = {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B + 2{J_3}}}{{kT}}}}{D_1} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}{D_2} + \\ {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B - 2{J_3}}}{{kT}}}}{D_3} + {e^{\frac{{ - 2{J_1} + 2{J_2}}}{{kT}}}}\left( {{D_4} + {D_6}} \right) + \\ {e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}}\frac{1}{2}\left( {{D_5} + {D_{10}}} \right) + {e^{\frac{{ - 2{J_1} + 2{J_2} + 2\mu B}}{{kT}}}}{D_8} + {{\rm{e}}^{\frac{{{\rm{2}}{{\rm{J}}_{\rm{1}}}{\rm{ + 2}}{{\rm{J}}_{\rm{2}}}{\rm{ + 2}}\mu {\rm{B + 2}}{{\rm{J}}_{\rm{3}}}}}{{{\rm{kT}}}}}}{D_9}12 \end{array}$ | (12) |
| ${\boldsymbol{D}_1} = \left[{\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \end{array}} \right]$ | (13) |
| ${\boldsymbol{D}_2} = \left[{\begin{array}{*{20}{c}} 0&1&1&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \end{array}} \right]$ | (14) |
| ${\boldsymbol{D}_3} = \left[{\begin{array}{*{20}{c}} 0&0&0&1 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \end{array}} \right]$ | (15) |
| ${\boldsymbol{D}_4} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 1&0&0&0 \\ 1&0&0&0 \\ 0&0&0&0 \end{array}} \right]$ | (16) |
| ${\boldsymbol{D}_5} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&1&1&0 \\ 0&1&1&0 \\ 0&0&0&0 \end{array}} \right]$ | (17) |
| ${\boldsymbol{D}_6} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&1 \\ 0&0&0&1 \\ 0&0&0&0 \end{array}} \right]$ | (18) |
| ${\boldsymbol{D}_7} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 1&0&0&0 \end{array}} \right]$ | (19) |
| ${\boldsymbol{D}_8} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&1&1&0 \end{array}} \right]$ | (20) |
| ${\boldsymbol{D}_9} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&0 \\ 0&0&0&1 \end{array}} \right]$ | (21) |
| ${{\mathbf{\boldsymbol{D}}}_{10}} = \left[{\begin{array}{*{20}{c}} 0&0&0&0 \\ 0&1&-1&0 \\ 0&-1&0&0 \\ 0&0&0&0 \end{array}} \right]$ | (22) |
If Dj multiples V1, the results are:
| ${\boldsymbol{D}_1}{\boldsymbol{V}_1} = {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B + 2{J_3}}}{{kT}}}}{\boldsymbol{D}_1} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}{\boldsymbol{D}_2} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B - 2{J_3}}}{{kT}}}}{\boldsymbol{D}_3}$ | (23) |
| $\begin{gathered} {\boldsymbol{D}_2}{\boldsymbol{V}_1} = 2{e^{\frac{{ - 2{J_1} + 2{J_2}}}{{kT}}}}\left( {{\boldsymbol{D}_1} + {\boldsymbol{D}_3}} \right) + \\ \left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}}{e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right){\boldsymbol{D}_2} \\ \end{gathered} $ | (24) |
| ${\boldsymbol{D}_3}{\boldsymbol{V}_1} = {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B - 2{J_3}}}{{kT}}}}{\boldsymbol{D}_1} + {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B}}{{kT}}}}{\boldsymbol{D}_2} + {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B + 2{J_3}}}{{kT}}}}{\boldsymbol{D}_3}$ | (25) |
| ${\boldsymbol{D}_4}{\boldsymbol{V}_1} = {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B + 2{J_3}}}{{kT}}}}{\boldsymbol{D}_4} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}{\boldsymbol{D}_5} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B - 2{J_3}}}{{kT}}}}{\boldsymbol{D}_6}$ | (26) |
| $\begin{gathered} {\boldsymbol{D}_5}{\boldsymbol{V}_1} = 2{e^{\frac{{ - 2{J_1} + 2{J_2}}}{{kT}}}}\left( {{\boldsymbol{D}_4} + {\boldsymbol{D}_6}} \right) + \hfill \\ \left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} + {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right){\boldsymbol{D}_5} \hfill \\ \end{gathered} $ | (27) |
| $\begin{gathered} {\boldsymbol{D}_6}{\boldsymbol{V}_1} = {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B - 2{J_3}}}{{kT}}}}{\boldsymbol{D}_4} + {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B}}{{kT}}}}{\boldsymbol{D}_5} + \\ {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B + 2{J_3}}}{{kT}}}}{\boldsymbol{D}_6} \\ \end{gathered} $ | (28) |
| $\begin{gathered} {\boldsymbol{D}_7}{\boldsymbol{V}_1} = {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B + 2{J_3}}}{{kT}}}}{\boldsymbol{D}_7} + {e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}{\boldsymbol{D}_8} + \\ {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B - 2{J_3}}}{{kT}}}}{\boldsymbol{D}_9} \\ \end{gathered} $ | (29) |
| $\begin{gathered} {\boldsymbol{D}_8}{\boldsymbol{V}_1} = {e^{\frac{{ - 2{J_1} + 2{J_2}}}{{kT}}}}2\left( {{\boldsymbol{D}_7} + {\boldsymbol{D}_9}} \right) + \hfill \\ \left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} + {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right){\boldsymbol{D}_8} \hfill \\ \end{gathered} $ | (30) |
| $\begin{gathered} {D_9}{V_1} = {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B - 2{J_3}}}{{kT}}}}{D_7} + \hfill \\ {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B}}{{kT}}}}{D_8} + {e^{\frac{{2{J_1} + 2{J_2} + 2\mu B + 2{J_3}}}{{kT}}}}{D_9} \hfill \\ \end{gathered} $ | (31) |
| ${\boldsymbol{D}_{10}}{\boldsymbol{V}_1} = \left( {{e^{\frac{{2{J_1} + 2{J_2} + 2\mu B}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right){\boldsymbol{D}_{10}}$ | (32) |
From above, it can be seen that D1V1-D3V1 can be expressed as the linear combinations of D1-D3. D4V1-D6V1 can be expressed as the linear combinations of D4-D6. D7V1-D9V1 can be expressed as the linear combinations of D7-D9. D10V1 can be expressed with D10. Now D1-D10 are divided into 4 groups: D1-D3, D4-D6, D7-D9 and D10. DjV1 can be expressed as the linear combinations of Dk from the same group. This means we can calculate V1N3 based on separate groups of D1-D10. We can establish a transfer matrix V2 to describe the relationship between Dj from the same group:
| ${\boldsymbol{V}_2} = {e^{\frac{{2{J_2}}}{{kT}}}}\left[{\begin{array}{*{20}{c}} {{e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_1} - 2\mu B}}{{kT}}}}}&{{e^{\frac{{ - 2{J_3} + 2{J_1} - 2\mu B}}{{kT}}}}} \\ {2{e^{\frac{{ - 2{J_1}}}{{kT}}}}}&{{e^{\frac{{2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{ - 2{J_3} - 2{J_1}}}{{kT}}}}}&{{e^{\frac{{ - 2{J_1}}}{{kT}}}}} \\ {{e^{\frac{{ - 2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_1} + 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}} \end{array}} \right]$ | (33) |
| $\left( {{a_1}{\boldsymbol{D}_1} + {a_2}{\boldsymbol{D}_2} + {a_3}{\boldsymbol{D}_3}} \right)\boldsymbol{V}_1^n = {a_{10}}{\boldsymbol{D}_1} + {a_{11}}{\boldsymbol{D}_2} + {a_{12}}{\boldsymbol{D}_3}$ | (34) |
| $\left[{\begin{array}{*{20}{c}} {{a_{10}}}&{{a_{11}}}&{{a_{12}}} \end{array}} \right]{\text{ = }}\left[{\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}} \end{array}} \right]\boldsymbol{V}_2^n$ | (35) |
| $\left[{{a_4}{\boldsymbol{D}_4} + {a_5}{\boldsymbol{D}_5} + {a_6}{\boldsymbol{D}_6}} \right]\boldsymbol{V}_1^n = {a_{13}}{\boldsymbol{D}_4} + {a_{14}}{\boldsymbol{D}_5} + {a_{15}}{\boldsymbol{D}_6}$ | (36) |
| $\left[{\begin{array}{*{20}{c}} {{a_{13}}}&{{a_{14}}}&{{a_{15}}} \end{array}} \right]{\text{ = }}\left[{\begin{array}{*{20}{c}} {{a_4}}&{{a_5}}&{{a_6}} \end{array}} \right]\boldsymbol{V}_2^n$ | (37) |
| $\left[{{a_7}{\boldsymbol{D}_7} + {a_8}{\boldsymbol{D}_8} + {a_9}{\boldsymbol{D}_9}} \right]\boldsymbol{V}_1^n = {a_{16}}{\boldsymbol{D}_7} + {a_{17}}{\boldsymbol{D}_8} + {a_{18}}{\boldsymbol{D}_9}$ | (38) |
| $\left[{\begin{array}{*{20}{c}} {{a_{16}}}&{{a_{17}}}&{{a_{18}}} \end{array}} \right]{\text{ = }}\left[{\begin{array}{*{20}{c}} {{a_7}}&{{a_8}}&{{a_9}} \end{array}} \right]\boldsymbol{V}_2^n$ | (39) |
| ${\boldsymbol{D}_{10}}\boldsymbol{V}_1^n = {\left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right)^n}{\boldsymbol{D}_{10}}$ | (40) |
Now we can use V2 to calculate V1N3:
| $\begin{gathered} \boldsymbol{V}_1^{{N_3}} = {\boldsymbol{V}_1}\boldsymbol{V}_{^1}^{{N_3} - 3} = \hfill \\ \left( {{a_1}{\boldsymbol{D}_1} + {a_2}{\boldsymbol{D}_2} + {a_3}{\boldsymbol{D}_3} + {a_4}{\boldsymbol{D}_4} + {a_5}{\boldsymbol{D}_5} + } \right. \hfill \\ \left. {{a_6}{\boldsymbol{D}_6} + {a_7}{\boldsymbol{D}_7} + {a_8}{\boldsymbol{D}_8} + {a_9}{\boldsymbol{D}_9} + {a_{19}}{\boldsymbol{D}_{19}}} \right)\boldsymbol{V}_1^{{N_3} - 1} = \hfill \\ {a_{10}}{\boldsymbol{D}_1} + {a_{11}}{\boldsymbol{D}_2} + {a_{12}}{\boldsymbol{D}_3} + {a_{13}}{\boldsymbol{D}_4} + {a_{14}}{\boldsymbol{D}_5} + \hfill \\ {a_{15}}{\boldsymbol{D}_6} + {a_{16}}{\boldsymbol{D}_7} + {a_{17}}{\boldsymbol{D}_8} + {a_{18}}{\boldsymbol{D}_9} + {a_{19}} \hfill \\ {\left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right)^{{N_3} - 1}}{\boldsymbol{D}_{10}} \hfill \\ \end{gathered} $ | (41) |
where
| $\left[{\begin{array}{*{20}{c}} {{a_{10}}}&{{a_{11}}}&{{a_{12}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}} \end{array}} \right]\boldsymbol{V}_2^{{N_3} - 1}$ | (42) |
| $\left[{\begin{array}{*{20}{c}} {{a_{13}}}&{{a_{14}}}&{{a_{15}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{a_4}}&{{a_5}}&{{a_6}} \end{array}} \right]\boldsymbol{V}_2^{{N_3} - 1}$ | (43) |
| $\left[{\begin{array}{*{20}{c}} {{a_{17}}}&{{a_{18}}}&{{a_{19}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{a_7}}&{{a_8}}&{{a_9}} \end{array}} \right]\boldsymbol{V}_2^{{N_3} - 1}$ | (44) |
The trace of V1N3 is:
| $\begin{gathered} Tr\left( {V_2^{{N_3} - 1}} \right) = {\left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right)^{{N_3} - 1}} = \hfill \\ \left[{\begin{array}{*{20}{c}} {{a_1}}&{{a_2}}&{{a_3}} \end{array}} \right]V_2^{{N_3} - 1}\left[{\begin{array}{*{20}{c}} 1 \\ 0 \\ 0 \end{array}} \right] + 2\left[{\begin{array}{*{20}{c}} {{a_4}}&{{a_5}}&{{a_6}} \end{array}} \right]V_2^{{N_3} - 1}\begin{array}{*{20}{c}} 0 \\ {\left[1 \right]} \\ 0 \end{array} + \hfill \\ \left[{\begin{array}{*{20}{c}} {{a_7}}&{{a_8}}&{{a_9}} \end{array}} \right]V_2^{{N_3} - 1}\left[{\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right] + \hfill \\ 2{a_{19}}{\left( {{e^{\frac{{ - 2{J_1} + 2{J_2} + 2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right)^{{N_3} - 1}} \hfill \\ \end{gathered} $ | (45) |
Here V2N3-1 can be written as:
| $\boldsymbol{V}_2^{{N_3} - 1} = G\left[{\begin{array}{*{20}{c}} {\alpha _1^{{N_3} - 1}}&{}&{} \\ {}&{\alpha _2^{{N_3} - 1}}&{} \\ {}&{}&{\alpha _3^{{N_3} - 1}} \end{array}} \right]{\boldsymbol{G}^{ - 1}}$ | (46) |
where α1, α2, α3 are the eigenvalues of V2; G is a 3×3 matrix consisted of 3 eigenvectors corresponding to α1, α2, α3.
| $\begin{gathered} {\alpha _1} = {e^{\frac{{2{J_2}}}{{kT}}}}\left[{{a_{21}} - \frac{{{a_{20}}}}{{3{a_{21}}}} + \frac{1}{3}\left( {{e^{\frac{{2{J_3} + 2{J_1} - 2\mu B}}{{kT}}}} + } \right.} \right.{e^{\frac{{2{J_3} - 2{J_1}}}{{kT}}}} + \hfill \\ \left. {\left. {{e^{\frac{{ - 2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}} \right)} \right] \hfill \\ \end{gathered} $ | (47) |
| $\begin{gathered} {\alpha _2} = {e^{\frac{{2{J_2}}}{{kT}}}}\left[{{a_{21}}{e^{i\frac{{ - 2\pi }}{3}}} - \frac{{{a_{20}}}}{{3{a_{21}}{e^{i\frac{{ - 2\pi }}{3}}}}} + \frac{1}{3}\left( {{e^{\frac{{2{J_3} + 2{J_1} - 2\mu B}}{{kT}}}} + } \right.} \right.{e^{\frac{{2{J_3} - 2{J_1}}}{{kT}}}} + \hfill \\ \left. {\left. {{e^{\frac{{ - 2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}} \right)} \right] \hfill \\ \end{gathered} $ | (48) |
| $\begin{gathered} {\alpha _3} = {e^{\frac{{2{J_2}}}{{kT}}}}\left[{{a_{21}}{e^{i\frac{{ - 2\pi }}{3}}} - \frac{{{a_{20}}}}{{3{a_{21}}{e^{i\frac{{ - 2\pi }}{3}}}}}} \right. + \frac{1}{3}\left( {{e^{\frac{{2{J_3} + 2{J_1} - 2\mu B}}{{kT}}}} + } \right. \hfill \\ \left. {\left. {{e^{\frac{{2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{ - 2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}} \right)} \right] \hfill \\ \end{gathered} $ | (49) |
| $\begin{gathered} {a_{20}} = {e^{\frac{{4{J_1}}}{{kT}}}}\left[{\left( {{e^{\frac{{4{J_3}}}{{kT}}}} - {e^{\frac{{ - 4{J_3}}}{{kT}}}}} \right) - \frac{1}{3}{e^{\frac{{4{J_3}}}{{kT}}}}{{\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right)}^2}} \right] + \hfill \\ \frac{1}{3}{e^{\frac{{2{J_3}}}{{kT}}}}\left( {{e^{\frac{{2\mu B}}{{kT}}}} + {e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 5{e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right) - \hfill \\ \frac{1}{3}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} + {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}{e^{\frac{{4{J_1}}}{{kT}}}} \hfill \\ \end{gathered} $ | (50) |
| ${a_{21}} = \sqrt[3]{{ - \frac{1}{2}{a_{22}} \pm \sqrt {{a_{23}}} }}$ | (51) |
| $\begin{gathered} {a_{22}} = {e^{\frac{{6{J_1}}}{{kT}}}}\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right)\left[{\frac{1}{3}} \right.{e^{\frac{{2{J_3}}}{{kT}}}}\left( {{e^{\frac{{4{J_3}}}{{kT}}}} - {e^{\frac{{ - 4{J_3}}}{{kT}}}}} \right) - \hfill \\ \left. {\frac{2}{{27}}{e^{\frac{{6{J_3}}}{{kT}}}}\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right)} \right] + \hfill \\ \frac{1}{9}{e^{\frac{{2{J_1}}}{{kT}}}}{e^{\frac{{4{J_3}}}{{kT}}}}\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 5{e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right){\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right)^2} + \hfill \\ \frac{1}{3}{e^{\frac{{2{J_1}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} + {e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right)^2}\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right) + \hfill \\ {\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right)^3} + \frac{1}{9}{e^{\frac{{2{J_1}}}{{kT}}}}{e^{\frac{{2{J_3}}}{{kT}}}}\left( {{e^{\frac{{2\mu B}}{{kT}}}} + } \right. \hfill \\ \left. {{e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)\left( {{e^{\frac{{2{J_3}}}{{kT}}}} + {e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right)\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 5{e^{{e^{\frac{{ - 2{J_3}}}{{kT}}}}}}} \right) - \hfill \\ {e^{\frac{{ - 6{J_1}}}{{kT}}}}\frac{2}{{27}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^3} \hfill \\ \end{gathered} $ | (52) |
| $\begin{array}{l} {a_{23}}{ = ^1}108{e^{\frac{{12{J_1}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}\left[ { - 4{e^{\frac{{ - 4{J_3}}}{{kT}}}} - } \right.\\ \left. {{e^{\frac{{4{J_3}}}{{kT}}}}{{\left( {{e^{\frac{{2\mu B}}{{kT}}}} + {e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)}^2}} \right]{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2} + \\ \frac{1}{{54}}{e^{\frac{{8{J_1}}}{{kT}}}}{e^{\frac{{6{J_3}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - } \right.\\ \left. {3{e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right) \times \left[ {{{\left( {{e^{\frac{{2\mu B}}{{kT}}}} + {e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)}^2} - } \right.\\ \left. {4{e^{\frac{{ - 4{J_3}}}{{kT}}}}\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 3{e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)\left( {{e^{\frac{{2{J_3}}}{{kT}}}} + {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)} \right] - \\ \frac{1}{{108}}{e^{\frac{{4{J_1}}}{{kT}}}}{e^{\frac{{8{J_3}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}{\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}}} \right)^4} + \\ \frac{1}{{54}}{e^{\frac{{4{J_1}}}{{kT}}}}{e^{\frac{{4{J_3}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}\left( {{e^{\frac{{4{J_3}}}{{kT}}}} + 14 - } \right.\\ \left. {24 - 14{e^{\frac{{ - 4{J_3}}}{{kT}}}} + {e^{\frac{{ - 8{J_3}}}{{kT}}}}} \right) + \\ \frac{1}{{54}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}{\left( {{e^{\frac{{2\mu B}}{{kT}}}} + {e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)^2} \times \\ \left[ {{e^{\frac{{6{J_3}}}{{kT}}}}\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 3{e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)} \right.{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - 2{e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2} + \\ \frac{1}{{108}}{e^{\frac{{ - 4{J_1}}}{{kT}}}}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}{\left( {{e^{\frac{{2{J_3}}}{{kT}}}} + {e^{\frac{{ - 2{J_3}}}{{kT}}}}} \right)^2}\left[ {4\left( {{e^{\frac{{4{J_3}}}{{kT}}}}} \right.} \right. - \\ \left. {\left. {{e^{\frac{{ - 4{J_3}}}{{kT}}}}} \right) - {e^{\frac{{4{J_3}}}{{kT}}}}{{\left( {{e^{\frac{{2\mu B}}{{kT}}}} + {e^{\frac{{ - 2\mu B}}{{kT}}}}} \right)}^2}} \right] \end{array}$ | (53) |
If we insert Eqs. (46)-(53) into Eq. (45), then we can get the expression of Tr(V1N3):
| $\begin{gathered} Tr\left( {\boldsymbol{V}_1^{{N_3}}} \right) = \alpha _1^{{N_3}} + \alpha _2^{{N_3}} + \alpha _3^{{N_3}} + \hfill \\ {\left( {{e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}} - {e^{\frac{{ - 2{J_1} + 2{J_2} - 2{J_3}}}{{kT}}}}} \right)^{{N_3}}} \hfill \\ \end{gathered} $ | (54) |
The eigenvalues of V1 are λ1, λ2, λ3, λ4, the trace of V1N3 is:
| $Tr\left( {\boldsymbol{V}_1^{{N_3}}} \right) = \lambda _1^{{N_3}} + \lambda _2^{{N_3}} + \lambda _3^{{N_3}} + \lambda _4^{{N_3}}$ | (55) |
We can see the similarity between two forms of Tr(V1N3), and α1, α2, α3 are also the eigenvalues of V1. Then we need to prove that V2 contains the largest eigenvalue of V1. To prove this, we set J1=J2=J3=B=0, and then V2 in Eq. (33) and V1 becomes:
| ${\boldsymbol{V}_2}\left| {_{{J_1} = {J_2} = {J_3} = B = 0} = \left[{\begin{array}{*{20}{c}} 1&1&1 \\ 2&2&2 \\ 1&1&1 \end{array}} \right]} \right.$ | (56) |
| ${\boldsymbol{V}_1}\left| {_{{J_1} = {J_2} = {J_3} = B = 0} = \left[{\begin{array}{*{20}{c}} 1&1&1&1 \\ 1&1&1&1 \\ 1&1&1&1 \\ 1&1&1&1 \end{array}} \right]} \right.$ | (57) |
Obviously, the eigenvalues of V2 in Eq. (56) are 4 and 0. The eigenvalues of V1 in Eq.(57) are also 4 and 0.For other combinations of N1, N2, the first row elements of V2|J1=J2=J3=B=0 are 1, and the second row elements are f1>0, and the third row elements are f2>0, the jth row elements are fj>0.The summation of f1f2f3… is: f1+f2+f3+…=2N1N2-1. This means the eigenvalues of V2|J1=J2=J3=B=0 are 2N1N2 and 0. The eigenvalues of V1|J1=J2=J3=B=0 are also 2N1N2 and 0. Now we know V2|J1=J2=J3=B=0 contains the largest eigenvalue of V1|J1=J2=J3=B=0. When J1, J2, J3, B change to non-zero values, the eigenvalues of 2N1N2 and 0 will change too, the eigenvalue that originates from 2N1N2 will keep being larger than other eigenvalues that originates from zero. For example, when N1=N2=1, the two eigenvalues are:
| $\begin{gathered} {\lambda _1} = \frac{1}{2}{e^{\frac{{2{J_1} + 2{J_2}}}{{kT}}}}\left[{{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}} + } \right. \hfill \\ \left. {\sqrt {{e^{\frac{{2{J_3}}}{{kT}}}}\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}} - 2} \right) + 4{e^{\frac{{ - 2{J_3}}}{{kT}}}}} } \right] \hfill \\ \end{gathered} $ | (58) |
| $\begin{gathered} {\lambda _2} = \frac{1}{2}{e^{\frac{{2{J_1} + 2{J_2}}}{{kT}}}}\left[{{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}} - } \right. \hfill \\ \left. {\sqrt {{e^{\frac{{2{J_3}}}{{kT}}}}\left( {{e^{\frac{{ - 2\mu B}}{{kT}}}} + {e^{\frac{{2\mu B}}{{kT}}}} - 2} \right) + 4{e^{\frac{{ - 2{J_3}}}{{kT}}}}} } \right] \hfill \\ \end{gathered} $ | (59) |
where λ1 remains the largest eigenvalue when J1, J2, J3, B change to non-zero values. Therefore V2 still contains the largest eigenvalue of V1. Obviously the order of V2 is smaller than the order of V1.
From above, we can summarize the steps to establish a smaller transfer matrix V2. Firstly, we change the form of V1 into:
| ${\boldsymbol{V}_1} = \sum\limits_n {{e^{\frac{{{p_n}{J_1} + {q_n}{J_2} + {r_n}\mu B + {s_n}{J_3}}}{{kT}}}}} {\boldsymbol{D_n}}$ | (60) |
where (p1, q1, r1, s1), (p2, q2, r2, s2) … are different combinations of integers; D1, D2, D3… are a series of 2N1N2×2N1N2 matrixes. The elements of Dn are either 0 or 1. Then we try to establish a group of matrixes F1, F2, F3…. The product of FkV1 can be expressed as the linear combinations of F1, F2, F3… from the same group:
| ${\boldsymbol{F_k}}{\boldsymbol{V}_1} = \sum\limits_1 {{\boldsymbol{F}_l}{b_{k,l}}} $ | (61) |
where bk, l are obviously the elements of the transfer matrix V2.
To start off, we use F1 as the first member of this group and then we will add new members to the group later:
| ${\boldsymbol{F}_1} = \left[{\begin{array}{*{20}{c}} 1&0& \cdots \\ 0&0& \cdots \\ \vdots & \vdots & \vdots \end{array}} \right]$ | (62) |
All elements of F1 are zero except the leftmost element in the first row.
Assuming there are w matrixes of the group at some points: F1, F2, …Fw, if for a certain pair of Fk and Dl, FkDl cannot be expressed as the linear combination of F1, F2, …Fw, and then we construct a new matrix Fw+1 to add to the group as a new member:
| ${\boldsymbol{F}_{w + 1}} = {\boldsymbol{F}_k}{\boldsymbol{D}_l} - \sum\limits_{m = 1}^w {\frac{{{\boldsymbol{F}_m}\left[{\left( {{\boldsymbol{F}_k}{D_l}} \right) \cdot {F_m}} \right]}}{{{\boldsymbol{F}_m} \cdot {\boldsymbol{F}_m}}}} $ | (63) |
where the sign · means the point product between two matrixes
Then we try to find another FkDl that cannot be expressed as the linear combination of F1, F2, …Fw+1. Repeat this process over and over. Eventually we will come to a point that for any pair of Fk and Dl, FkDl can be expressed as the linear combinations of F1, F2, …FNc, this means the group of matrixes is complete. Here we have used Nc to denote the total number of the complete group. Nc is also the order of the transfer matrix V2.
All elements of F1, F2, …FNc are zero except the first row. For simplicity, we can use 1×2N1N2 vectors F1′, F2′, …FNc′ instead of the 2N1N2×2N1N2 matrixes. For the convenience of calculation, we make the elements of F1′, F2′, …FNc′ either 0 or 1. For example, assuming there is a pair of Fj′ and Fk′ like this:
| ${{F'}_j} = \left[{\begin{array}{*{20}{c}} 1&9&1&1 \end{array}} \right]$ | (64) |
| ${{F'}_k} = \left[{\begin{array}{*{20}{c}} 3&{ - 1}&3&3 \end{array}} \right]$ | (65) |
For these two vectors, the elements of the first, third and fourth spots have the same value, but the second spot has a different value. So for Fj′, we set the value of the second spot at zero. But for Fk′, we set the value of the second spot at 1, we turn the elements of other spots into zero:
| ${{\boldsymbol{F}'}_j} = \left[{\begin{array}{*{20}{c}} 1&0&1&1 \end{array}} \right]$ | (66) |
| ${{\boldsymbol{F}'}_k} = \left[{\begin{array}{*{20}{c}} 0&1&0&0 \end{array}} \right]$ | (67) |
The principle is: the 2N1N2 spots of the vectors are divided into Nc areas. Each vector has a different corresponding area. For a certain vector, all elements of that corresponding area are 1, other spots are zero. For a certain spot, there is only one Fk′ of which the element of that spot is 1.
After this modification, all elements of F1′, F2′, …FNc′ are either 0 or 1.
The elements of V2 are:
| ${b_{k,m}} = \left[{{{\left( {{{\boldsymbol{F}'}_{\rm{k}}}{\boldsymbol{V}_1}} \right)}^{\rm{T}}}{{\boldsymbol{F}'}_m}} \right]/\left( {{{\boldsymbol{F}'}_m}^T{{\boldsymbol{F}'}_m}} \right)$ | (68) |
In the case of N1=N2=1, V2 is identical to V1. If N1=2, N2=1, V2 is:
| $\begin{array}{l} {V_2}\left| {_{{N_1} = 2,{N_2} = 1} = } \right.\\ {e^{\frac{{2{J_2}}}{{kT}}}}\left[{\begin{array}{*{20}{c}} {{e^{\frac{{2{J_1} + 2{J_2} - 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_1} - 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_3} + 2{J_1} - 2\mu B}}{{kT}}}}}\\ {2{e^{\frac{{ - 2{J_1}}}{{kT}}}}}&{{e^{\frac{{2{J_3} - 2{J_1}}}{{kT}}}} + {e^{\frac{{ - 2{J_3} - 2{J_1}}}{{kT}}}}}&{2{e^{\frac{{ - 2{J_1}}}{{kT}}}}}\\ {{e^{\frac{{ - 2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_1} + 2\mu B}}{{kT}}}}}&{{e^{\frac{{2{J_3} + 2{J_1} + 2\mu B}}{{kT}}}}} \end{array}} \right]69\\ \end{array}$ | (69) |
If N1=3, N2=1, V2 is:
| ${V_2}\left| {_{{N_1} = 2,{N_2} = 1} = } \right.\\{e^{\frac{{3{J_2}}}{{kT}}}}\left[{\begin{array}{*{20}{c}} {{e^{\frac{{2{J_1} + 2{J_2} + 3{J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} - 3\mu B + {J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} - 3\mu B - {J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} - 3\mu B - 3{J_3}}}{{kT}}}}}\\ {{e^{\frac{{ - {J_1} - \mu B + {J_3}}}{{kT}}}}}&{2{e^{\frac{{ - {J_1} - \mu B - {J_3}}}{{kT}}}} + {e^{\frac{{ - {J_1} - \mu B + 3{J_3}}}{{kT}}}}}&{2{e^{\frac{{ - {J_1} - \mu B + {J_3}}}{{kT}}}} + {e^{\frac{{ - {J_1} - \mu B - 3{J_3}}}{{kT}}}}}&{3{e^{\frac{{ - {J_1} - \mu B - {J_3}}}{{kT}}}}}\\ {3{e^{\frac{{ - {J_1} + \mu B + {J_3}}}{{kT}}}}}&{2{e^{\frac{{ - {J_1} + \mu B + {J_3}}}{{kT}}}} + {e^{\frac{{ - {J_1} + \mu B - 3{J_3}}}{{kT}}}}}&{2{e^{\frac{{ - {J_1} + \mu B - {J_3}}}{{kT}}}} + {e^{\frac{{ - J + \mu B + 3{J_3}}}{{kT}}}}}&{3{e^{\frac{{ - {J_1} + \mu B + {J_3}}}{{kT}}}}}\\ {{e^{\frac{{3{J_1} + 3\mu B - 3{J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} + 3\mu B - {J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} + 3\mu B + {J_3}}}{{kT}}}}}&{{e^{\frac{{3{J_1} + 3\mu B + 3{J_3}}}{{kT}}}}} \end{array}} \right]$ | (70) |
Here are the orders of V2 in some cases:
N1=3, N2=1: NC=4
N1=4, N2=1: NC=6
N1=2, N2=2: NC=7
N1=5, N2=1: NC=8
N1=6, N2=1: NC=13
N1=3, N2=2: NC=13
N1=7, N2=1: NC=18
N1=8, N2=1: NC=30
N1=4, N2=2: NC=34
N1=9, N2=1: NC=46
N1=3, N2=3: NC=36
N1=10, N2=1: NC=78
N1=5, N2=2: NC=78
N1=11, N2=1: NC=126
N1=12, N2=1: NC=224
N1=6, N2=2: NC=237
N1=4, N2=3: NC=158
N1=13, N2=1: NC=380
N1=14, N2=1: NC=687
N1=7, N2=2: NC=687
N1=15, N2=1: NC=1 224
N1=5, N2=3: NC=707
N1=16, N2=1: NC=2 250
N1=8, N2=2: NC=2 299
N1=4, N2=4: NC=1 459
N1=17, N2=1: NC=4 112
N1=18, N2=1: NC=7 685
N1=9, N2=2: NC=7 685
N1=6, N2=3: NC=4 236
N1=19, N2=1: NC=14 310
From above, we can see that NC is much smaller than 2N1N2.
3 CalculationThe thermal-physical parameters we use in this paper are: J1=J2=J3=1 kJ/mol, μ=9.274 009 49×10-24 J/T, k=1.380 648 8×10-23 J/K, here μ is the magnetic momentum of an atom, and k is the Boltzmann's constant.
Fig. 1 shows how the specific heat per atom Cpa=C/N1N2N3 changes with temperature T and magnetic field intensity B. When B=0, Cpa gets to its largest value 1.94×10-23 J/K at T=47.966 K. But the overall maximum value for Cpa is 2.142 907×10-23J/K at T=49.178 K, B=±4.1715 T. We use TC to represent the critical temperature where Cpa gets to its maximum value. TC becomes larger when the value of magnetic field intensity B increases. If B=0, TC has its smallest value.
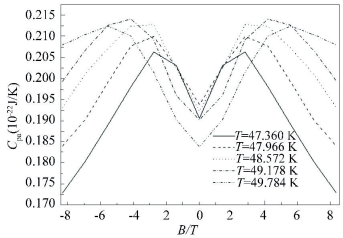
|
Figure 1 Cpa versus B with different temperature (N1=N2=4) |
Since we only calculate 3-dimensional Ising model of finite width, the value of Cpa is finite too. If N1 or N2 is infinite, the value of Cpa at TC will become infinite, but TC will approach to a certain value which is finite. TC is the temperature where phase transition happens. We use TX and BX to represent the temperature and magnetic field intensity where Cpa get to its maximum value. T0 is the temperature where Cpa get to its maximum value when B=0. Here's TX, BX and T0 in some cases:
N1=17, N2=1: TX=27.795 K, BX=±1.372T, T0=27.249 K
N1=16, N2=1: TX=27.598 K, BX=±1.135T, T0=27.245 K
N1=8, N2=2: TX=44.031 K, BX=±3.508T, T0=43.177 K
N1=4, N2=4: TX=49.080 K, BX=±4.426T, T0=48.063 K
N1=15, N2=1: TX=27.835 K, BX=±1.603T, T0=27.232 K
N1=5, N2=3: TX=48.466 K, BX=±5.222T, T0=47.192 K
N1=7, N2=2: TX=44.048 K, BX=±4.168T, T0=43.156 K
If N2=1, the model turns into 2-dimensional model. TX≈27.8 K, BX≈1.3 K, T0≈27.25 K. If the value of N1N2 does not change and N2 increases, TX, BX and T0 will become larger. We can see that in 3 dimensions, it needs higher temperature and magnetic field intensity to create phase transition. This is because the 3-dimensional interaction between atoms is stronger than that of 2-dimensional.
Fig. 2 shows the relationship between the magnetic momentum per atom Mpa=M/N1N2N3 and the magnetic field intensity B. We can see that Mpa becomes smaller when temperature increases. If B is large enough, Mpa will increase slower and approach a certain value. This is called magnetic saturation.

|
Figure 2 M versus B with different temperature (N1=N2=4) |
Fig. 3 shows the maximum value of Cpa in different cases when B=0. In this picture, we use T′=T-T0 instead of normal temperature T so that the maximum point of Cpa in different cases can meet together to show the difference, and T0 is the temperature where Cpa gets to its maximum value. We can see that when N1N2 increases, the maximum value of Cpa|B=0 becomes larger. If N1N2 is infinite, Cpa will becomes infinite at critical temperature TC. The value of TC changes with magnetic field intensity.

|
Figure 3 Cpain different cases when B=0, T′=T-T0 |
4 Conclusions
In this paper, we use the 2N1N2×2N1N2 matrix V1 to build a much smaller matrix V2 which contains the largest eigenvalue of V1. Then we obtain the largest eigenvalue of V2 and calculate the specific heat per atom Cpa and the magnetic momentum per atom Mpa. There exists a pair of T and B to make Cpa get to its maximum value. When N1N2 increases, the maximum value of Cpa|B=0 increases too.
| [1] |
Onsager L. Crystal statistics. I.A two-dimensional model with an order-disorder transition.
Physical Review, 1994 , 65 (3) : 117-119.
DOI:10.1103/PhysRev.65.117. ( 1) 1)
|
| [2] | Gao Zhan, Xu Jianhong, Wan Zhenlin. Critical behavior at the surface of a semi infinite mixed spin Ising system with surface random field and amorphism. Acta Physica Sinica, 1999 , 48 (11) : 2131-2136. |
| [3] |
Shao Yuanzhi, Lan Tu, Lin Guangming. Dynamical transition and tricritical points of 3D kinetic Ising spin system.
Acta Physica Sinica, 2001 , 50 (5) : 942-947.
( 1) 1)
|
| [4] |
Laabo M, Saber A, Benab M, et al. Temperature dependences of the order parameters of a magnetic Ising superlattice of two ferrowmagnet materials with spins μ=1/2 and S=1.
Chinese Physics B, 1999 , 8 (3) : 199-207.
( 1) 1)
|
| [5] |
Ni Jun, Gu Binglin. Ferrimagnetic phases of the Blume-Emery-Griffiths model and the potts model on the diamond lattice.
Chinese Physics B, 2000 , 9 (6) : 469-473.
DOI:10.1088/1009-1963/9/6/013 ( 1) 1)
|
| [6] | Deng Lingling, Yan Shilei. Critical properties of the transverse ferromagnetic spin system with random single-ion anisotropy. Chinese Physics B, 2002 , 11 (4) : 383-388. DOI:10.1088/1009-1963/11/4/313 |
| [7] |
Dickinson H, Yeomans J. Tricritical behaviour in a bond-dilute spin model.
Journal of Physics C, 1983 , 16 (2) : 345-349.
DOI:10.1088/0022-3719/16/2/017 ( 1) 1)
|
| [8] |
Ng Waiman, Barry J H. Cluster-variation method applied in the pair approximation to the S=1 Ising ferromagnet having additional single-ion-type uniaxial anisotropy.
Physical Review B, 1978 , 17 (9) : 3675-3681.
DOI:10.1103/PhysRevB.17.3675 ( 1) 1)
|
| [9] |
Chakraborty K G, Tucker J W. Linear chain approximation for an anisotropic cubic spin-one Ising model.
Physica A, 1986 , 137 (1) : 111-119.
DOI:10.1016/0378-4371(86)90066-X ( 1) 1)
|
| [10] |
Kaufman M, Kanner M. Random-field Blume-Capel model:mean-field theory.
Physical Review B, 1990 , 42 (4) : 2378-2385.
DOI:10.1103/PhysRevB.42.2378 ( 1) 1)
|
| [11] |
Liu Wuming, Wang Xiaobing, Pu Fucho, et al. Nonlinear dynamics of the magnetization in an anisotropic ferromagnet with a magnetic field.
Physical Review B, 1996 , 54 (5) : 4612-4621.
DOI:10.1103/PhysRevE.54.4612 ( 1) 1)
|
| [12] |
Jiang Xuefan, Li Jialiang, Zhong Jialin, et al. Effect of a crystal field on phase transitions in a spin-1 transverse Ising model.
Physical Review B, 1993 , 47 (2) : 827-835.
DOI:10.1103/PhysRevB.47.827 ( 1) 1)
|
| [13] |
El-Showk S, Paulos M, Poland D, et al. Solving the 3D Ising model with the conformal bootstrap.
Physical Review D, 2012 , 86 (3) : 025022.
DOI:10.1103/PhysRevD.86.025022 ( 1) 1)
|
| [14] |
Jin S B, Sen A, Sandvik A. Ashkin-Teller criticality and pseudo-first-order behavior in a frustrated Ising model on the square lattice.
Physical Review Letters, 2012 , 108 (4) : 045702.
DOI:10.1103/PhysRevLett.108.045702 ( 1) 1)
|
| [15] |
Wu X T, Izmailian N, Guo W A. Finite-size behavior of the critical Ising model on a rectangle with free boundaries.
Physical Review E, 2012 , 86 (4) : 041149.
DOI:10.1103/PhysRevE.86.041149 ( 1) 1)
|
| [16] |
Deviren B, Canko O, Keskin M. Kinetic Ising model in a time-dependent oscillating external magnetic field: effective-field theory.
Chinese Physics B, 2010 , 19 (5) : 050518.
DOI:10.1088/1674-1056/19/5/050518 ( 1) 1)
|
| [17] |
Heyl M, Polkovnikov A, Kehrein S. Dynamical quantum phase transitions in the transverse-field Ising model.
Physical Review Letters, 2013 , 110 (13) : 135704.
DOI:10.1103/PhysRevLett.110.135704 ( 1) 1)
|
| [18] |
Campo A, Rams M, Zurek W. Assisted finite-rate adiabatic passage across a quantum critical point: exact solution for the quantum Ising model.
Physical Review Letters, 2012 , 109 (11) : 115703.
DOI:10.1103/PhysRevLett.109.115703 ( 1) 1)
|
| [19] |
Ates C, Olmos B, Garrahan J, et al. Dynamical phases and intermittency of the dissipative quantum Ising model.
Physical Review A, 2012 , 85 (4) : 043620.
DOI:10.1103/PhysRevA.85.043620 ( 1) 1)
|
| [20] |
Zhang S, Li J, Bartell J, et al. Perpendicular magnetization and generic realization of the Ising model in artificial spin ice.
Physical Review Letters, 2012 , 109 (8) : 087201.
DOI:10.1103/PhysRevLett.109.087201 ( 1) 1)
|
| [21] |
Barnett L, Lizier J, Harre M, et al. Information flow in a kinetic Ising model peaks in the disordered phase.
Physical Review Letters, 2013 , 111 (17) : 177203.
DOI:10.1103/PhysRevLett.111.177203 ( 1) 1)
|
| [22] |
Schoelz J K, Xu P, Meunier V, et al. Graphene ripples as a realization of a two-dimensional Ising model: A scanning tunneling microscope study.
Physical Review B, 2015 , 91 (4) : 045413.
DOI:10.1103/PhysRevB.91.045413 ( 1) 1)
|
| [23] |
Dublenych Y. Ground states of the Ising model on the shastry-sutherland lattice and the origin of the fractional magnetization plateaus in rare-earth-metal tetraborides.
Physical Review Letters, 2012 , 109 (16) : 167202.
DOI:10.1103/PhysRevLett.109.167202 ( 1) 1)
|
| [24] |
Lau H, Grassberger P. Information theoretic aspects of the two-dimensional Ising model.
Physical Review E, 2013 , 87 (2) : 022128.
DOI:10.1103/PhysRevE.87.022128 ( 1) 1)
|
| [25] |
Langer J S. Ising model of a glass transition.
Physical Review E, 2013 , 88 (1) : 012122.
( 1) 1)
|
| [26] |
Fytas N G, Mayor V M. Universality in the three-dimensional random-field Ising model.
Physical Review Letters, 2013 , 110 (22) : 227201.
DOI:10.1103/PhysRevLett.110.227201 ( 1) 1)
|
| [27] |
Xu X T, Izmailian N, Guo W A. Finite-size behavior of the critical Ising model on a rectangle with free boundaries.
Physical Review E, 2013 , 86 (4) : 041149.
DOI:10.1103/PhysRevE.86.041149 ( 1) 1)
|
| [28] |
Corberi F, Lippiello E, Mukherjee A, et al. Crossover in growth law and violation of superuniversality in the random-field Ising model.
Physical Review E, 2012 , 85 (2) : 021141.
DOI:10.1103/PhysRevE.85.021141 ( 1) 1)
|
| [29] |
Powalski M, Coester K, Moessner R, et al. Disorder by disorder and flat bands in the kagome transverse field Ising model.
Physical Review B, 2013 , 87 (5) : 054404.
DOI:10.1103/PhysRevB.87.054404 ( 1) 1)
|
| [30] |
Damski B. Fidelity susceptibility of the quantum Ising model in a transverse field: The exact solution.
Physical Review E, 2013 , 87 (5) : 052131.
DOI:10.1103/PhysRevE.87.052131 ( 1) 1)
|
| [31] |
Bastidas V M, Emary C, Schaller G, et al. Nonequilibrium quantum phase transitions in the Ising model.
Physical Review A, 2012 , 86 (6) : 063627.
DOI:10.1103/PhysRevA.86.063627 ( 1) 1)
|
| [32] |
Henry L, Holdsworth P, Mila F, et al. Spin-wave analysis of the transverse-field Ising model on the checkerboard lattice.
Physical Review B, 2012 , 85 (13) : 134427.
DOI:10.1103/PhysRevB.85.134427 ( 1) 1)
|
| [33] |
Jin S B, Sen A, Guo W A, et al. Phase transitions in the frustrated Ising model on the square lattice.
Physical Review B, 2013 , 87 (14) : 144406.
DOI:10.1103/PhysRevB.87.144406 ( 1) 1)
|
 2016, Vol. 23
2016, Vol. 23



