2. School of Advanced Engineer, University of Science and Technology Beijing, Beijing 100083, China
Loop heat pipe (LHP) is known for high heat-transfer efficiency.It is widely used in miniature electric devices, especially the devices related to space technology[1-5]. The first LHP was developed and tested successfully by Maydanik in 1972[6]. LHPs are different from their sizes, shapes, materials and working fluids. In general, LHPs are classified into two types by the shape of the evaporator. One type is the LHP with a cylindrical evaporator, which is the most common LHP. The other is the LHP with a flat evaporator. It is recognized as a more advanced LHP in the aspect of the contact area with heat source [7]. The LHP with flat evaporator mainly consists of condenser, vapor pipe, liquid pipe and flat evaporator as shown in Fig. 1.

|
Figure 1 Schematic of a LHP with flat evaporator |
The performance of LHP was investigated with plenty of experiments[8-11], especially the performance of the LHP with a flat evaporator[12]. In the experiments, temperature oscillation was observed frequently during the operation of LHP in certain conditions[13]. This phenomenon has negative influence on the performance of LHP. For example, the temperature oscillation appearing during startup process delays the startup of LHP and even makes the startup fail[14]. Huang et al.[15]found that the oscillation in startup process happened when the input power was between critical heat load and minimal heat load. The temperature oscillation during startup was characterized as low-amplitude (no more than 1 K) and high-frequency. It was recognized as a result of the oscillation of the liquid front in the wick. Besides, temperature oscillation also occurred during operation[16-18]. The amplitude of this kind of temperature oscillation was also low, but the period and duration was much longer. The temperature oscillation during operation was supposed to be caused by the oscillation of the two-phase interface in the condenser. Temperature oscillation also happened with low-frequency and high-amplitude, which often lasted for hours. It happened in the case that the thermal mass evaporator was massive and the sink temperature kept very low.
The performance optimization of LHP has been studied by theoretical models. Some researches focused on building integrate model for the LHP [19-20]. Others researched the performance of some key components by building local mathematical models [21]. However, all the known researches ignored the investigation of temperature oscillation.
This paper aims to investigate the movement of the phase interface as the changed input power by a mass-spring-damper model. The model can be used to explain the high-frequency and low-amplitude temperature oscillation. Parameter analyses were performed to make suggestions for controlling the intensity and frequency of the temperature oscillation. The results were validated by experimental data in a literature [22].
2 Model Description 2.1 Mass-Spring-Damper Model of LHPThe mass-spring-damper model is based on the force balance of the liquid column in the sub-cooling region of the condenser and liquid line. The vapor columns in the vapor line and reservoir are treated as vapor springs respectively because of the compressibility of vapor. The liquid column is treated as a mass between the two vapor springs for the incompressibility of liquid. The two vapor springs press the liquid column from the opposite directions. The changed input power can be treated as an excitation for breaking the balance of the thermal equilibrium and pressure equilibrium. Fig. 2 illustrates the force balance of the column.
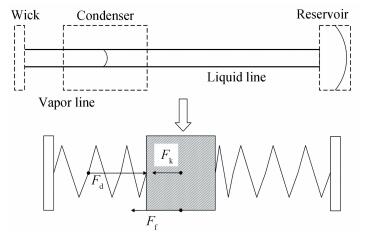
|
Figure 2 Schematic of mass-spring-damper model of LHP |
According to the Newton's second law analysis of the liquid column, it yields:
| $ M\frac{{{\text{d}}^{2}}x}{\text{d}{{t}^{2}}}={{F}_{\text{d}}}-{{F}_{\text{f}}}-{{F}_{\text{ }\!\!\kappa\!\!\text{ }}} $ | (1) |
where, M is the mass of the liquid column; x is the displacement, and t the time; Fd is the force disturbance caused by sudden heat load change; Ff is the friction force of the liquid column, and Fk is the elastic force of the vapor springs.
According to the law of Newton inner friction and the shear stress expression in laminar pipe flow[23], Ffcan be written as
| $ \begin{align} & {{F}_{\text{f}}}=\eta \frac{\text{d}x}{\text{d}t} \\ & \eta \text{=}8\text{ }\!\!\pi\!\!\text{ }{{\mu }_{1}}L \\ \end{align} $ | (2) |
where, η is the friction coefficient; μl is the dynamic viscosity of liquid, and L is the length liquid column.
Assuming the vapor pipe and the reservoir are thermal insulated, the two vapor springs experience isentropic processes. According to the equation of ideal gas state, the elastic force and the stiffness coefficient of the vapor springs can be described as linear[24], when the displacement of the liquid column is in a small range:
| $ \begin{align} & {{F}_{\text{ }\!\!\kappa\!\!\text{ }}}=\kappa x \\ & \kappa =\gamma p\frac{A_{\text{v}}^{2}}{{{V}_{\text{v}}}} \\ \end{align} $ |
where, κ is the stiffness coefficient of the vapor springs; p is the pressure; Av is the cross-sectional area of the vapor springs, and Vv is the volume of the vapor springs.
Since the vapor springs are in adiabatic condition, the coefficient γ can be taken as 1.4. As a disturbance term, Fd can be determined by calculating the pressure difference Δpd between the two surfaces of the wick[25].
| $ {{F}_{\text{d}}}=\Delta {{p}_{\text{d}}}{{A}_{1}} $ |
where, Al is the cross-sectional area of the liquid column. Substituting the expression of Fk and Ff in Eq. (1), it yields:
| $ \frac{{{\text{d}}^{2}}x}{\text{d}{{t}^{2}}}\text{+}2\beta \frac{\text{d}x}{\text{d}t}+\omega _{0}^{2}x=\frac{{{F}_{\text{d}}}}{M} $ | (3) |
| $ \beta =\frac{\eta }{2M} $ | (4) |
| $ {{\omega }_{0}}=\sqrt{\frac{\kappa }{M}} $ | (5) |
where, β is the damping factor, and ω0 is the natural frequency.
Solving Eq. (3) with Laplace transform and Inverse Laplace transform, the analytical solution can be achieved as:
| $ x=\frac{{{F}_{\text{d}}}-\varphi M\omega _{0}^{2}}{2M\omega _{0}^{2}\alpha }{{\text{e}}^{-\beta t}}\left[ {{\text{e}}^{-\alpha t}}\left( \beta -\alpha \right)-{{\text{e}}^{\alpha t}}\left( \beta +\alpha \right) \right]+\frac{{{F}_{\text{d}}}}{M\omega _{0}^{2}} $ |
| $ \alpha =\sqrt{{{\beta }^{2}}-\omega _{0}^{2}} $ |
where φ is the initial displacement.
2.2 Determination of State Parameters and PropertiesThe state parameters and properties of LHP are determined based on energy balance and thermodynamic relationships. In the LHP, pressure disturbance transports at local sound speed, which is much quicker than the heat transfer. It means the thermal state changes little when the liquid column reacts to the pressure disturbance, i.e. excitation. Therefore, the state parameters and properties involved in the mass-spring-damper model are all calculated in a steady state.
The following assumptions are made to simplify the mathematical model:
1) The LHP model is in adiabatic condition, i.e. no heat releases from the profile of the LHP to the ambient. The error produced from the adiabatic assumption can be ignored according to the experimental data of Singh et al. [22].
2) The heat transfer inside the casing of the evaporator and the reservoir is ignored.
3) The evaporation happens at the wick-groove interface.
4) The superheat is ignored. The evaporating temperature is the same as condensing temperature.
5) The water is treated as incompressible fluid in the LHP.
The simplified thermal network of the LHP model is shown in Fig. 3. For the evaporator, the total heat load Qin produced by the heat source dissipates in two ways: one is to heat the subcooled liquid Tco to the saturated temperature Ts; the other is to cause the evaporation at the wick-groove interface. The heat transfer process can by described by
| $ {{Q}_{\text{in}}}={{Q}_{\text{sen}}}+{{Q}_{\text{eva}}}+{{Q}_{\text{er}}} $ | (6) |
| $ \begin{align} & {{Q}_{\text{sr}}}={{\lambda }_{\text{sr}}}{{z}_{\text{wick}}}\left( {{T}_{\text{s}}}-{{T}_{\text{r}}} \right) \\ & {{Q}_{\text{eva}}}=\dot{m}\lambda \\ & {{Q}_{\text{sen}}}=\zeta {{C}_{\text{pl}}}\dot{m}\left( {{T}_{\text{s}}}-{{T}_{\text{co}}} \right) \\ \end{align} $ |
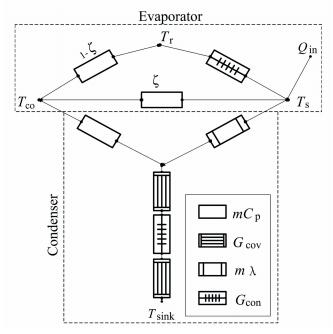
|
Figure 3 Thermal network of the LHP model |
where, Qsen is the sensible heat given to the subcooled liquid from the liquid pipe; Qevais the latent heat for evaporation; Qsr is the heat transferred from the groove to the reservoir; λsr is the thermal conductivity from the groove to the reservoir; zwick is the thickness of the wick; $\dot{m}$ is the mass flow rate; Tr is the temperature of the reservoir; Cpl is the fluid specific heat, and the coefficient ζ is the ratio of subcooled liquid entering the wick without having heat transfer to the total.
The coefficient ζ is surely influenced by the mass flow rate [26]. The coefficient ζ can be determined by a polynomial fitted by the data of Singh et al.[22].The coefficients of the fitted polynomial are shown in Table 1.
| Table 1 Coefficients of polynomial |
| $ \begin{align} & \zeta \text{=}{{C}_{0}}+{{C}_{1}}\dot{m}+{{C}_{\text{2}}}{{{\dot{m}}}^{2}}+{{C}_{\text{3}}}{{{\dot{m}}}^{\text{3}}}+{{C}_{\text{4}}}{{{\dot{m}}}^{\text{4}}}\text{+}{{C}_{\text{5}}}{{{\dot{m}}}^{\text{5}}}\text{+} \\ & \ \ \ \ {{C}_{\text{6}}}{{{\dot{m}}}^{\text{6}}} \\ \end{align} $ |
Since the liquid line is thermal isolated to the environment, the temperature of the water at the outlet of condenser Tco is equal to the temperature at the inlet of reservoir. The vapor in the reservoir is considered to be saturated. The saturated temperature can be described by Antoine equation[27] as follows:
| $ {{T}_{\text{s}}}\text{=}\frac{b}{a\ \text{lg}\left( {{p}_{\text{s}}}/\psi \right)}c+273.15 $ |
where, a, b, c are coefficients for the Antoine equation; ps is the saturate pressure, and ψ is the coefficient for unit conversion.
The pressure drops in the vapor line Δpv and liquid line, Δpv and Δpl, can be calculated by[28]:
| $ \Delta p=\frac{f}{2\rho D}{{\left( \frac{{\dot{m}}}{A} \right)}^{2}}L $ |
where, the friction factor f can be evaluated as:
| $ f=\left\{ \begin{matrix} 64/Re & Re\le 2\ 200 \\ 0.316\ R{{e}^{-0.25}} & 2\ 200 < Re < {{10}^{5}} \\ \end{matrix} \right. $ |
The condenser is usually a combination of two-phase region and sub-cooling region. Since the vapor pipe is considered as adiabatic, the vapor enters the two-phase region at the evaporating temperature Ts and condenses to saturated water in the two-phase region. The energy balance can be described as follows:
| $ \dot{m}\lambda =\frac{1}{1/{{h}_{\text{2p}}}+1/{{h}_{\text{sink}}}}\text{ }\!\!\pi\!\!\text{ }{{D}_{i}}{{L}_{\text{2p}}}\left( {{T}_{\text{s}}}-{{T}_{\text{sink}}} \right) $ |
where, λ is the latent heat; L2p is the length of the two-phase region in the condenser; Tsink is the heat sink temperature; h2p is the heat transfer coefficient of the two phase region; hsink is the heat transfer coefficient of the heat sink.
In the sub-cooling region, the saturated water is cooled to a lower temperature Tco and release sensible heat. The energy balance can be described by
| $ \begin{align} & \dot{m}{{C}_{\text{pl}}}\left( {{T}_{\text{s}}}-{{T}_{\text{co}}} \right)=\frac{1}{1/\left( {{h}_{\text{1}}}{{D}_{i}} \right)+1/\left( {{h}_{\sin k}}{{D}_{\text{o}}} \right)}. \\ & \ \ \ \ \ \ \ \ \ \ \ \text{ }\!\!\pi\!\!\text{ }\left( {{L}_{\text{c}}}-{{L}_{2\text{p}}} \right)\frac{{{T}_{\text{s}}}-{{T}_{\text{co}}}}{\ln \left( \frac{{{T}_{\text{s}}}-{{T}_{\text{sink}}}}{{{T}_{\text{co}}}-{{T}_{\text{sink}}}} \right)} \\ \end{align} $ | (10) |
where, hl is the heat transfer coefficient of the liquid; Do is the outer diameter of the condenser, and Lc is the length of the condenser.
To calculate the liquid temperature in the compensation chamber, Valeri et al.[29] divided the liquid entering the chamber into two parts. One part of the liquid enters the wick without having heat transfer with the water retained in the reservoir. The parameter ζ is used to represent the ratio of this part to the whole, and the rest is represented by (1-ζ). For the rest part, the energy balance can be described as follows:
| $ \left( 1-\zeta \right)\dot{m}{{C}_{\text{pl}}}\left( {{T}_{\text{r}}}-{{T}_{\text{co}}} \right)={{\lambda }_{\text{sr}}}{{z}_{\text{wick}}}\left( {{T}_{\text{s}}}-{{T}_{\text{r}}} \right) $ |
where, λsr is the heat conductance from the groove to the reservoir. The heat convection inside the wick is neglected since it does not play a major role comparing with heat conduction. The heat conductance can be described as follows[30]:
| $ {{\lambda }_{\text{sr}}}={{\lambda }_{\text{1}}}{{\left( {{\lambda }_{\text{1}}}/{{\lambda }_{\text{wm}}} \right)}^{-{{\left( 1-\varepsilon \right)}^{0.59}}}} $ |
where, λl and λwm represent the heat conductance of the liquid and the wick material, respectively; ε is the porosity of the wick.
2.3 Solving ProcessThe mass-spring-damper model is solved with MATLAB. The complete process is showed in Fig. 4. An iterative procedure is used to solve the state parameters by initializing an assumed mass flow rate m0. The deduced mass flow rate is corrected by Eq. (6). The iteration terminates when the relative error of mass flow rate is less than 0.1%.

|
Figure 4 Thermal network of the LHP model |
The disturbance of the input heat flux Qin can lead to the change of state parameters and the thermal conductivity of the working mass. Therefore, the mass-spring-damper model is re-solved when the input heat flux Qin is changed. At the end of the procedure, an array is used to record and output the results.
3 Model ValidationThe model was validated with the structural parameters and experimental data of a LHP prototype designed by Singh et al. [22]. The LHP prototype with a flat-disk shaped evaporator is operated in horizontal orientation. The wick is made of nickel, the porosity of which is 75%. The evaporator is made of stainless steel, and the working fluid is water. For the condenser, the heat sink temperature is 295.15 K, and the heat transfer coefficient of the heat sink is 2 000 W/ (m2·K). Table 2 shows the detail parameters of the LHP prototype.
Fig. 5 presents the comparison between the model results and experimental data of the saturation temperature ts in the groove. Good agreement can be seen in Fig. 5. Generally, the results of the model are a little bit higher than the experimental data. It is because that the model is built based on the assumption of adiabatic condition to the ambient, i.e. no heat releases from the profile of the LHP to the ambient.
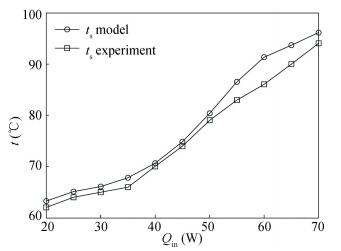
|
Figure 5 Comparison between the model and the data from Singh[22] |
| Table 2 Parameters of the LHP prototype |
4 Results and Discussion
Fig. 6 shows the change of the input power. The power is increased from 20 W to 70 W in increments of 5 W, which is corresponded with the condition of the reference[22]. The time interval of the power change is set as 5 minutes.
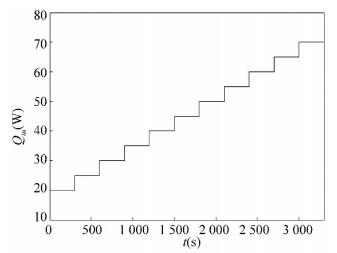
|
Figure 6 Step change of the input power |
4.1 Temperature Variation
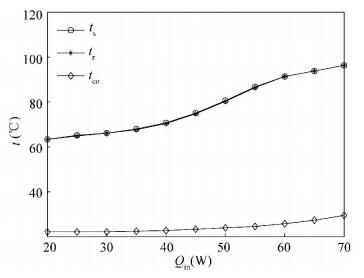
The variation of ts, tr and tco in the power range from 20 W to 70 W as plotted in Fig. 7. In Fig. 7, the three temperatures show nonlinear growth as the input power Qin increases. The temperature of the condenser outlet tco keeps steady and is equal to the temperature of cooling water serving as the heat sink when the input power is lower than 40 W. For higher input power, tco starts to increase with it. Correspondingly, ts starts to increase substantially either.
|
Figure 7 Temperature distribution in different input powers |
Usually, the cooled objects are supposed to work in a narrow temperature range. The above results suggests that to keep the temperature of the subcooled fluid at the outlet of the condenser stable is the premise to avoid substantial fluctuation of the cooled objects. This goal can be achieved by adjusting the amount of cooling water.
For all the input heat loads, the saturated temperature in the groove ts and the temperature of reservoir tr are always very close to each other as seen in Fig. 5. It suggests that the temperature in the reservoir is dominated by the heat leak through the wick. The result agrees well with the experimental data of Singh et al[22]. Some researchers [32] calculated tr as the local saturated temperature. In this way, tr is either close to ts since the high latent heat of water leads to small mass flow rate and tiny pressure drop in the LHP.
4.2 Oscillation of the Liquid ColumnDifferent from solid mass-spring model, the size of the liquid column and the vapor springs changes during the step changes of the input power and makes the model complex. Therefore, the position of the phase interface in the condenser is evaluated in each step change.
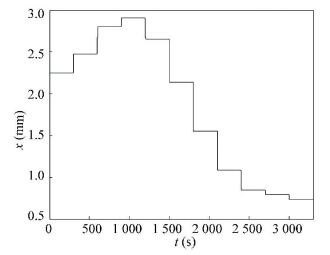
The displacement of the liquid column caused by the step change of input power is shown in Fig. 8. When the input power increases from 20 W to 35 W, the liquid column moves to the reservoir. When the input power increases more, the liquid column tends to move far from the reservoir. It should be noticed that the increment of displacement was not uniform during the input power change.
|
Figure 8 Displacement of the liquid column caused by input power |
In this study, the LHP was made of opaque material, so that the liquid column oscillation could not be observed. Begg[31] ever researched the phase interface movement of a loop thermosyphon, which structure and size were similar to the LHP studied by this paper. He changed the heat load and recorded the phase interface movement photographically. Although the magnitude was different, the liquid column oscillation was also observed when the heat load was increased as shown in Fig. 9.

|
Figure 9 Photographic record of phase interface movement by Begg[31] |
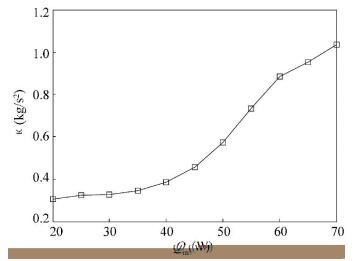
The displacement of the liquid column is decided not only by the pressure difference on the two opposite sides, but also by the stiffness coefficient of the two vapor springs. When the input power steps up, the pressure difference on the two opposite sides fluctuates as shown in Fig. 10, and the stiffness coefficient is raised consistently as presented in Fig. 11. The increased stiffness coefficient improves the elastic force of the vapor spring and makes it harder to be pressed by the pressure difference. It is easy to know that the size of the vapor spring in the reservoir reduces as the liquid ratio in the reservoir increases, which makes the stiffness coefficient increase. The inference of the liquid ratio is also discussed in other researches[32]. After the input power reaches over 35 W, the stiffness coefficient increases sharply while the pressure difference decreases. In result, the position of the liquid column moves back to the condenser.

|
Figure 10 Tendency of the pressure difference with input power |
|
Figure 11 Tendency of the stiffness coefficient with input power |
The change of the displacement of the liquid column presents the phenomenon that the liquid column oscillated during the step change of the input power. The oscillation of the liquid column is considered as the reason of the temperature oscillation at the outlet of the condenser [15, 22].
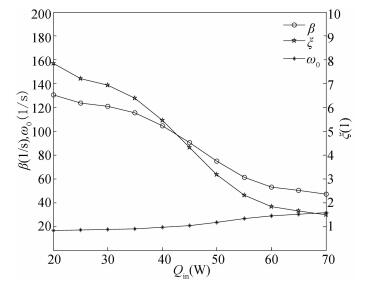
4.3 Variation of Vibration ParametersFig. 12 shows the variation of the damping ratio ξ, damping factor β and natural frequency ω0 with the change of input power.
|
Figure 12 Tendency of the coefficients with input power |
The damping factor β reflects the friction force in the vibration of the liquid column. It is clear that β reduced as the input power increased from Eqs. (2) and (4). The main reason is that the length of the liquid column decreases as the input power increases. Generally, β was high enough to make the oscillating system become stable quickly. This characteristic makes reasonable the assumption that the running parameters, such as temperature and pressure, are stable during the solution of the mass-spring-damper model.
The natural frequency ω0 represents the frequency of the oscillation of the liquid column after it suffers an external pulse disturbance, such as input power change. Fig. 12 shows ω0 keeps increasing. It is mainly caused by the increased stiffness coefficient according to Eq. (5). The tendency is consistent with the tendency of the temperature oscillation observed by Singh[22]. Since the fluctuation of the phase interface is the main reason of the temperature oscillation at the outlet of condenser[33], the tendency of the natural frequency can be used as a reference of the frequency of temperature oscillation at the condenser outlet.
The damping ratio ξ is the ratio of the damping factor β to the natural frequency ω0, which definition is shown as follows:
| $ \xi =\frac{\beta }{{{\omega }_{0}}} $ |
The relative value of damping ratio ξ to 1 determines the possibility that the system presents oscillation in response to excitation. When ξ > 1, the system is an over-damping system, and oscillation will not be induced by excitation. When ξ=1, the system is in critical damping state, and oscillation will not be induced by excitation either. When ξ < 1, the system is in under-damping state, and oscillation can be induced by excitation.
As shown in Fig. 12, the damping ratio decreases from much greater than 1 to close but still higher than 1 in the input power changing range. The tendency suggests that the temperature at the outlet of the condenser oscillates intensively when the input power is in the higher range. This result is consistent with the experimental data of Singh[22].
5 ConclusionsA mass-spring-damper model was built to simulate the oscillation of the liquid column and the temperature in a LHP. The liquid column was treated as the mass of the oscillating system, and the vapor columns at the two opposite sides of the liquid column were treated as vapor springs. This model can be used to describe the movement of the liquid column with the changed input power. The results suggested that the movement of the liquid column was influenced by the pressure difference applied on the liquid column and the stiffness coefficients of the vapor springs.
The damping factor was high enough to make the oscillating system become stable quickly. Therefore, it is reasonable to employ the thermal state parameters of the LHP in a steady condition based on energy balance, thermodynamic relationships and some reasonable assumptions during the solution of the mass-spring-damper model. The model was validated with experimental data from the literature and was used to simulate the temperature variation with the input power from 20 W to 75 W.
According to the model, the temperature oscillation at the outlet of the condenser can be weakened by increasing the mass of the liquid column and keeping the temperature at the outlet of the condenser steady.
| [1] |
Baker C L, Grob E W, McCarthy T V, et al. Geoscience laser altimetry system (GLAS) on-orbit flight report on the propylene loop heat pipes (LHPs).
AIP Conference Proceedings, 2004 , 699 (1) : 88-95.
( 0) 0)
|
| [2] |
Goncharov K A. Loop heat pipes in thermal control systems for "Obzor" spacecraft. 25th International Conference on Environmental Systems. San Diego, CA, 1995.
( 0) 0)
|
| [3] |
Goncharov K A, Kolesnikov V A. Development of propylene LHP for spacecraft thermal control systems.Proceedings of 12th International Heat Pipe Conference.Moscow, Russia, 2002. 171-176.
( 0) 0)
|
| [4] |
Maidanik Y F, Fershtater Y G, Goncharov K A. Capillary-pump loop for the systems of thermal regulation of spacecraft.
ESA, 1991 , 1 : 87-92.
( 0) 0)
|
| [5] |
Maydanik Y F, Fershtater Y G, Pastukhov V G. Thermoregulation of loops with capillary pumping for space use. SAE Paper, 1992.
( 0) 0)
|
| [6] |
Heat Pipe, USSR Inventors Certificate 449213.Moscow: Union of Soviet Socialist Republics, 1974.
( 0) 0)
|
| [7] |
Maydanik Y F. Loop heat pipes.
Applied Thermal Engineering, 2005 , 25 (5/6) : 635-657.
( 0) 0)
|
| [8] |
Figus C, Pullet C, Supper W. Development of miniaturized fluid loops in Astrium.Proceedings of International Two-phase Thermal Control Technology Workshop.El Segundo, CA, 2001.
( 0) 0)
|
| [9] |
Maydanik Y F, Vershinin S V, Chernyshova M A. Development and tests of miniature loop heat pipes with a flat evaporator. Proceedings of 30th International Conference on Environmental Systems and 7th European Symposium on Space Environmental Control Systems.Toulouse, France, 2000.
( 0) 0)
|
| [10] |
Maydanik Y F, Vershinin S V, Gerhart C. Miniature LHPs with a flat and a cylindrical evaporator-which one is better?Proceedings of International Two-Phase Thermal Control Technology Workshop.Noordwijk, The Netherlands, 2003.
( 0) 0)
|
| [11] |
Wang S, Huo J, Zhang X, et al. Experimental study on operating parameters of miniature loop heat pipe with flat evaporator.
Applied Thermal Engineering, 2012 , 40 : 318-325.
DOI:10.1016/j.applthermaleng.2012.02.029 ( 0) 0)
|
| [12] |
Chen B B, Liu W, Liu Z C, et al. Experimental investigation of loop heat pipe with flat evaporator using biporous wick.
Applied Thermal Engineering, 2012 , 42 : 34-40.
DOI:10.1016/j.applthermaleng.2012.03.006 ( 0) 0)
|
| [13] |
Li J, Wang D, Peterson G P. Experimental studies on a high performance compact loop heat pipe with a square flat evaporator.
Applied Thermal Engineering, 2010 , 30 (6/7) : 741-752.
( 0) 0)
|
| [14] |
Gai D, Liu Z, Liu W, et al. Operational characteristics of miniature loop heat pipe with flat evaporator.
Heat and Mass Transfer, 2009 , 46 (2) : 267-275.
DOI:10.1007/s00231-009-0563-0 ( 0) 0)
|
| [15] |
Huang B J, Huang H H, Liang T L. System dynamics model and startup behavior of loop heat pipe.
Applied Thermal Engineering, 2009 , 29 (14/15) : 2999-3005.
( 0) 0)
|
| [16] |
Chen Y, Groll M, Mertz R, et al. Steady-state and transient performance of a miniature loop heat pipe.
International Journal of Thermal Sciences, 2006 , 45 (11) : 1084-1090.
DOI:10.1016/j.ijthermalsci.2006.02.003 ( 0) 0)
|
| [17] |
Ku J. High frequency low amplitude temperature oscillations in loop heat pipe operation.33rd International Conference on Environmental Systems.Vancouver, B.C., Canada, 2003.
( 0) 0)
|
| [18] |
Li J, Lv L. Performance investigation of a compact loop heat pipe with parallel condensers.
Experimental Thermal and Fluid Science, 2015 , 62 : 40-51.
DOI:10.1016/j.expthermflusci.2014.12.001 ( 0) 0)
|
| [19] |
Chuang P. An Improved Steady-state Model of Loop Heat Pipes Based on Experimental and Theoretical Analyses. Pennsylvania State University, 2003.
( 0) 0)
|
| [20] |
Delil A, Baturkin V, Gorbenko G, et al. Modelling of a miniature loop heat pipe with a flat evaporator.Proceedings of the 32nd International Conference on Environmental Systems.2002.
( 0) 0)
|
| [21] |
Fang T, Ming T, Tso C P, et al. Analysis of non-uniform heat loads on evaporators with loop heat pipes.
International Journal of Heat and Mass Transfer, 2014 , 75 : 313-326.
DOI:10.1016/j.ijheatmasstransfer.2014.03.061 ( 0) 0)
|
| [22] |
Singh R, Akbarzadeh A, Mochizuki M. Operational characteristics of a miniature loop heat pipe with flat evaporator.
International Journal of Thermal Sciences, 2008 , 47 (11) : 1504-1515.
DOI:10.1016/j.ijthermalsci.2007.12.013 ( 0) 0)
|
| [23] |
Krause E.Fluid Mechanics.Springer Berlin Heidelberg, 2005.
( 0) 0)
|
| [24] |
Zheng M, Chen X, Lin Y. Dynamical model and characteristics analysis of air spring.
Transactions of the Chinese Society of Agricultural Machinery, 2008 , 39 (5) : 10-14.
( 0) 0)
|
| [25] |
Xu W, He L, Shuai C, et al. Stiffness calculation and dynamic simulation of air spring.Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.California, 2005. 1395-1399.
( 0) 0)
|
| [26] |
Lin G, Li N, Bai L, et al. Experimental investigation of a dual compensation chamber loop heat pipe.
International Journal of Heat and Mass Transfer, 2010 , 53 (15/16) : 3231-3240.
( 0) 0)
|
| [27] |
Majer V, Svoboda V, Pick J.Heats of Vaporization of Fluids.Amsterdam: Elsevier, 1989.
( 0) 0)
|
| [28] |
Bai L, Lin G, Zhang H, et al. Mathematical modeling of steady-state operation of a loop heat pipe.
Applied Thermal Engineering, 2009 , 29 (13) : 2643-2654.
DOI:10.1016/j.applthermaleng.2008.12.040 ( 0) 0)
|
| [29] |
Vlassov V V, Riehl R R. Mathematical model of a loop heat pipe with cylindrical evaporator and integrated reservoir.
Applied Thermal Engineering, 2008 , 28 (8/9) : 942-954.
( 0) 0)
|
| [30] |
Siedel B, Sartre V, Lefèvre F. Complete analytical model of a loop heat pipe with a flat evaporator.
International Journal of Thermal Sciences, 2015 , 89 : 372-386.
DOI:10.1016/j.ijthermalsci.2014.11.014 ( 0) 0)
|
| [31] |
Begg E K, Transport Phenomena in Micro/Miniature Channels for Two Phase Flow Heat Transfer Devices Including Heat Pipes and Fuel Cells. University of Connecticut, 2003.
( 0) 0)
|
| [32] |
Zhang X, Huo J, Wang S. Experimental investigation on temperature oscillation in a miniature loop heat pipe with flat evaporator.
Experimental Thermal and Fluid Science, 2012 , 37 : 29-36.
DOI:10.1016/j.expthermflusci.2011.09.010 ( 0) 0)
|
| [33] |
Zhang H, Lin G, Ding T, et al. Experimental investigation on temperature oscillation of loop heat pipes.
Journal of Beijing University of Aeronautics and Astronautics, 2005 , 31 (2) : 116-120.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


