2. Jiangsu Province Collaborative Innovation Center of Modern Urban Traffic Technologies, Nanjing 210096, China
There is a significant need for tools to enable the evaluation of the conventional public transit networks at the planning and management stage. One considerable approach for appraising public transportation systems is the study of the network [1-3], and the network structure indicator is one of the most important indicators in conventional public transit network evaluation. The attribute “conventional” will be omitted in the following contents, implying that terms like “transit” are equal to “conventional public transit”. In order to effectively make assessments, it is suggested all network structure indicators be reasonable and comprehensive in reflecting all aspects of network performance[4-5].
Among these network structure indicators, the no-linear coefficient is a most frequently-used one, aiming at evaluating the detour of a bus line. Li et al. employed the no-linear coefficient as an important indicator to evaluate the transit system based on GIS technology and provided corresponding decisions to improve the efficiency of public transportation systems in Xiangtan City, China[6]. In addition, the no-linear coefficient is usually selected as a constraint in transit route and network optimization problems. Zhu, for example, presented a practical model to optimize a transit network, which took maximal direct traveler density as the objective and with no-linear coefficient as the constraints [7]. Also, the transit routing problem was analyzed by Xi in engineering practice and a shortest-path routing method was put forward with the restriction of no-linear coefficient[8]. Studies on zigzagging of bus routes have something to do with the no-linear coefficient as well. Kho found that zigzagging was efficient in the remote ridership areas if the number of passengers already on board was lower compared with the outlying passengers requesting corridor service, which was reached by analytical cost models for no-zigzagging and zigzagging bus routing schemes [9]. Therefore, in some cases, a moderate detour of bus lines is cost-efficient.
However, the no-linear coefficient is commonly used for evaluation, attempts to quantify the rationality of the indicator have been few in number. Meanwhile, the network density is known to evaluate the coverage intensity of a transit network and commonly used together with the no-linear coefficient[10]. There should be also an indicator that can reflect the network coverage homogeneity as well. Just as the relationship between sample mean and variance, the indicator to evaluate the coverage homogeneity of a transit network is indispensable, which could be used along with the network density indicator. To model network coverage homogeneity, targeted regions for network evaluation are made clear and several measure centers in these regions could be selected respectively. In this way, the study on the condition of change of the network density from these centers to their surroundings in certain regions is related to the coverage homogeneity. If the rate of change of the network density is low, it may indicate that the transit network does not cover the region with a great concentration but is homogeneously distributed.
Given the analysis above, in this paper, the realistic no-linear coefficient γRNL is put forward to make up the limitation of traditional no-linear coefficient indicator. Then, the length dimension (LD), which acts as the rate of change of the network density for public transit, is also proposed to reflect the coverage homogeneity of a transit network. Both of the two indicators are easy to understand and calculate, and they are proved to be valid and practical through a small contrived transit network. The objective of this study is to improve the rationality and comprehensiveness of the indicator system for transit network structure evaluation.
2 Realistic No-Linear Coefficient 2.1 No-Linear Coefficient and Its FunctionA bus line needs to be somewhat circuitous between its two terminals to satisfy the traffic demand on the way. The circuitous degree, however, cannot be excessively large because it may make passengers travel for extra longer distance and more delay time accordingly. The no-linear coefficient of a bus line is defined as the ratio of the actual distance between its two terminals to the spatial straight line distance. For a special ring-shaped bus line, its no-linear coefficient is measured by two bus stops that are the most distant or distribute a great number of passengers[11-12]. This indicator is designed to reflect the circuitous degree of a bus line. In this paper, the no-linear coefficient defined above is renamed as idealized no-linear coefficient γINL.
From the definition, it is obvious that the shape of a bus line is close to straight line when γINL is around 1. The larger γINL is, the more circuitous the bus line is. In general, it is required that γINL should not be too large and usually not exceed 1.4 [13]. At present, γINL is one of the most pivotal indicators in evaluating network structure for a transit network. The dilemma is that the idealized layout of a transit network should satisfy most of the travel demand while γINL should be as small as possible within a limited scope. However, the advantage of the γINL indicator is that it is easy to understand and calculate, thus, γINL of each bus line in a transit network is usually figured out to make comparison and selection among different layout schemes in engineering practice.
2.2 Realistic No-Linear Coefficient IndicatorThe indicator γINL, however, has some limitations. For example, it cannot remove the influence of barriers in a city or topography. To be specific, γINL is typically larger than 1 in most cases, namely with the value range:
| $ {{\gamma }_{\text{INL}}}\in \left[ k,+\infty \right.)\left( k > 1 \right) $ | (1) |
where γINL represents the idealized no-linear coefficient.
When barriers in a city are in great scale, the value of γINL is far larger than 1, implying that k is a fairly large number (e.g.1.4). The cases are not scarce around the world, such as the Golden Gate Park in San Francisco, U.S., the West Lake in Hangzhou, China, the Purple Mountain in Nanjing, China, etc. As a result, γINL of some bus lines around these barriers probably exceeds 1.4, not conforming to the national standardized document [13]. Actually, it is probably impossible to set a bus line between two certain stations around the barriers with the standardized document obeyed. In addition, γINL of bus lines in cities with numerous or huge barriers are generally larger than those of others, though it does not mean that the layout of their transit networks is not as optimal as that of others.
To remove the influence of barriers exerting on no-linear coefficient and make it evaluate public transit network structure more objectively, the modified indicator, realistic no-linear coefficient γRNL, is proposed to replace INL in this paper. γRNL of a bus line is defined to be the ratio of the actual distance between its two terminals to the distance of shortest path based on road networks between them. Similarly, γRNL of a special ring-shaped line could be worked out. According to the definition, the formula of γRNL is deduced:
| $ {{\gamma }_{\text{RNL}}}=\frac{{{D}_{\text{A}}}}{{{D}_{\text{S}}}} $ | (2) |
where γRNL represents the realistic no-linear coefficient, DA is the distance between two terminals of a bus line, DS is the shortest path distance between two terminals of a bus line.
The difference between γRNL and γINL lays in the denominator, γRNL is not necessarily affected by barriers or topography in a city because shortest path based on road networks takes this factor into consideration as well, which offsets that in the numerator. The value range of γRNL is fixed:
| $ {{\gamma }_{\text{RNL}}}\in [1,+\infty ) $ | (3) |
It values 1 only if the bus line is set along the shortest path between two terminals. Compared with γINL, γRNL improves it greatly and keeps the good original nature. Obviously, γRNL can make up for γINL and solve the detour problem caused by the barriers well. As an indicator of urban public transportation network, it has a better environmental situation practicality. The only shortcoming is the complexity to get the shortest distance between two terminals. In practice, engineers can built bus network model based on Transcad, Visum, Cube or other software to get shortest distance matrix between the bus stations easily, which can greatly simplify the calculation of γRNL.
3 Length Dimension 3.1 Fractal TheoryThe concept of “fractal” was firstly put forward when the length of the coast of Britain was analyzed in depth. It was found that many geographical curves are statistically self-similar.In addition, the fractal dimension was proposed to characterize self-similarity[14-15]. Self-similarity, a characteristic that an object is similar to itself which gets locally amplified, is the basic property of Fractal Theory. It means the object always has more subtle and precise structure no matter how it is observed from different angles. The theoretical foundation of Fractal Theory is Fractal Geometry, which differs from traditional Euclidean Geometry in that it is not limited to geometry space with integer dimension. West had an insight into the fourth dimension of life based on Fractal Geometry rather than Euclidean Geometry, indicating the distinctive advantages of the concept of fractal[16].
It is evinced that the city is a typical self-similar system according to the related research at home and abroad. The growth and succession of a city takes place at different levels of scale-free domain which means targeted objects have nothing to do with scale and their properties keep constant no matter how the unit of measure changes. This “self-similarity” reflects the universal law of urban space form, thus, many researches focus on fractal characteristics. The fractal of transportation network is one of the most important spatial fractal, and it is widely applied to research on transportation network, traffic flow theory, etc[17]. There are mainly three basic fractal dimensions to reflect the fractal characteristics of urban road network structure: length-radius fractal dimension, branch-radius fractal dimension and space correlated dimension. Among them, length-radius fractal dimension is relatively most developed and broadly used to measure traffic network fractal [18]. It is the reflection of the characteristics of network density variation.
3.2 Length-Radius Fractal ModelThe following proportional relationship exists among the length (L), area (S) and volume (V) of a geometry on the basis of the theory of Plane Geometry:
| $ {{L}^{\frac{1}{1}}}\propto {{S}^{\frac{1}{2}}}\propto {{V}^{\frac{1}{3}}}\propto {{M}^{\frac{1}{d}}} $ | (4) |
where M stands for the generalized volume and d (d > 0) is Euclidean dimension. Supposing M equals S, then d values 2. Actually, d is unrestricted to positive integer and changes along with the change of M. When the measurement M of a geometry has fractal characteristics, the corresponding d is defined as fractal dimension.
It can be assumed that the network of public transit has fractal characteristics since the road network is proved to possess evident property of fractal[18]. The public transportation network inherits the fractal characteristics of the road network within a certain range, because the layout of public transportation network depends on the road network. Under the assumption, a circular planar region close-up with an area S is shown in Fig. 1. Owing to the directly-proportional relationship between the area and the square of radius in a circle, we obtain:
| $ {{L}_{\text{b}}}=k\cdot {{r}^{d}} $ | (5) |
|
Figure 1 Circular areas in a region |
where k (k > 0) is a constant in Eq.(5), and d is called length-radius fractal dimension because it is derived from network length and radius of a region. The length-radius fractal dimension can be referred to as length dimension LD.
LD reflects the condition of change on the density for a transit network in the whole city or a certain region of the city, which is measured from a measure center that is a CBD center or an integrated transportation hub in general. This statement can be validated through the deformation and derivative of Eq.(5):
| $ D=\frac{{{L}_{\text{b}}}}{{{r}^{2}}}=k\cdot {{r}^{d-2}} $ | (6) |
| $ \frac{\text{d}D}{\text{d}r}=k\left( d-2 \right)\cdot {{r}^{d-3}} $ | (7) |
where D is the density of the transit network.
The derivative in Eq.(7) reflects the rate of change of transit network density. Judging from common sense, the density is supposed to decrease from the measure center to surrounding areas when a CBD center or an integrated transportation hub is selected as the measure center. Nonetheless, the density probably decreases at first followed by a trend of increase if there are several CBD areas or transportation hubs in the city. In this case, the fractal characteristics should be significant only in certain regions that could not cover several CBD areas or transportation hubs. (The method to preliminarily validate the significance of fractal is presented in chapter 3.3) Therefore, when fractal characteristics are not insignificant, it is obtained:
| $ k\left( d-2 \right)\cdot {{r}^{d-3}} < 0 $ | (8) |
k must be larger than zero, so it turned out:
| $ d < 2 $ | (9) |
The decreasing rate of transit network density becomes slower when the value of LD gets closer to 2. So the role and function of LD which shows the condition of change of the network density gets confirmed.
In addition, Eq.(5) is further analyzed:
| $ \frac{\text{d}{{L}_{\text{b}}}}{\text{d}r}=kd\cdot {{r}^{d-1}} $ | (10) |
| $ \frac{{{\text{d}}^{2}}{{L}_{\text{b}}}}{{{\text{d}}^{2}}r}=kd\left( d-1 \right)\cdot {{r}^{d-2}} $ | (11) |
Given d is larger than 0, the derivative in Eq.(10) is larger than 0 as well, which means that the total length of transit network increases along with the increase of the radius. This finding coincides with the real situation, supporting the length-radius fractal model to some extent. The second derivative in Eq.(11) reflects the rate of the decreasing rate of total network length. When 0 < d < 1, the increase of total network length has a trend of reducing its speed. When 1 < d < 2, a trend of raise in the increasing rate is observed. The increasing rate keeps constant when exactly d=1.
3.3 Length Dimension IndicatorBased on the analysis above, when the fractal characteristics of a transit network are significant in the certain region (e.g., the whole city or a district), the range of LD value is:
| $ d\in \left( 0,2 \right) $ | (12) |
It can be concluded that:
1) The closer d gets to 0, the faster the network density decreases along with the increase of the radius.
2) When d is larger than 1, the increasing rate of total network length increases along with the increase of the radius.
3) It is ideal when d is larger than 1 but less than 2, especially close to 2 as far as possible.
Economic indicators, however, are supposed to draw special attention when d is close to 2 and it is suggested that the balance between passenger volume and different kinds of cost should be reasonably taken into account. In general, LD acts as the rate of change of the network density based on the analysis above.
The method to figure out the LD indicator is presented below. Regression analysis is used to achieve the purpose. We take the logarithm at both sides of Eq.(5):
| $ \ln \ {{L}_{\text{b}}}=d\ln r+C $ | (13) |
where C is a constant. The total length of transit network in a region determined by different length of radius is calculated through spatial analysis, thus, a series of data points could be obtained as shown in Fig. 2 [13]. Then, the regression analysis is conducted while d, the length dimension, is determined by calibrating Eq.(13). The fractal characteristics in a region are evident when the regression model has a good level of significance, and vice versa. Therefore, this significance level acts as a preliminary determination of the significance of fractal characteristics. There may exist some problems in determining the measure center and radius, and it is suggested that one should adjust measure radius before selecting another measure center when the regression model shows insignificant. The length of the shortest radius in a set of concentric circles should not be too small if it aimed at analyzing the attenuation of the transit network from the center area to its surroundings. The transit network density, otherwise, probably increases along with the increase of radius in a relatively small area around the measure center. Meanwhile, the length of the longest radius in a set of concentric circles should not be too large so as to prevent the region from covering several CBD areas or transportation hubs. In addition, if the regression model is significant but LD turns out to be out of its range value, it is believed that there is something wrong in determining LD. The selection of measure center, the calculation of total network length and other factors related to the method are probably inaccurate, which ought to be checked comprehensively.
|
Figure 2 Numerous circular areas to obtain data points |
4 Example and Analysis
A contrived transit network is used in this section to test the validity and practicability of the two proposed network structure indicators. The layout of the network is shown in Fig. 3. Some major stops of those bus lines are represented by letters in Fig. 3. Among these stops, A and B represent two transportation hubs. The same nodes and edges in the graph are passed by upstream and downstream directions of one bus line. Assumptions are made to simplify the problem-solving process in which length of bus lines can be figured out conveniently. Firstly, bus stops are located at intersections. Secondly, bus stops are located in the same surface. Thirdly, the alignment of bus lines is approximately horizontal and vertical. Accordingly, point Z, directed line ZQ and ZR, are set to be the origin of coordinate, the positive direction of X axis and Y axis, respectively. The coordinates of each bus stop could be settled in this plane rectangular coordinate system as follows in Table 1. Note that there is no bus line at the edge RU, ET, VW and MQ. The information about the eight bus lines in the network is given in Table 2.

|
Figure 3 Layout of the contrived transit network |
| Table 1 Bus stops and their coordinates |
| Table 2 Transit routes of eight bus lines |
Firstly, γRNL and γINL of the bus line AQ and RB are calculated respectively and compared, as shown in Table 3.
| Table 3 Results of γRNL and γINL |
Then, the LD of transportation hub A and B are figured out respectively. At first, the minimum measure radius is set to 800 meters and the maximum is 2 400 meters with a step of 400 meters referring to the literature [18], the total lengths of all bus lines in the circle area are calculated. It is suggested the radius reasonably have a wide value range, which leads to sufficient number of data points, so as to ensure the reliability of the regression model derived from Fractal Theory.
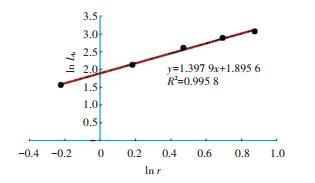
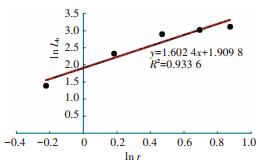
Given the contrived network, assuming that the above five radius are enough to guarantee the reliability of the regression model. The results of total network length (Lb) are calculated in Table 4. Then the regression model is established on condition that the unit of radius is transformed into kilometer, and two regression curves are shown in Figs. 4 and 5.
|
Figure 4 Regression curve of the measure center A |
|
Figure 5 Regression curve of measure center B |
| Table 4 Results of total network length with different radius |
The R-square of regression equation of the bus stop A is 0.995 8, of the bus stop B is 0.933 6, implying that the model significance of bus stop B is a bit lower than the bus stop A. It indicates an obscurity for the fractal characteristics around the stop B. Assuming that the stop B is a large transportation hub indeed, then it can be asserted that the problem lies in selecting minimum radius judging from the characteristics of scatters in Fig. 5. Accordingly, the length of minimum radius change to 1 600 meters while other elements remain unchangeable. On the basis of Table 5, the regression model of the fractal characteristics around the stop B is reestablished as is shown in Fig. 6, which is followed by the update results of LD presented in Table 6.

|
Figure 6 Regression curve of measure center B |
| Table 5 Results of total network length of measure center B |
| Table 6 Results of LD and significance of regression model |
Both the two models are highly significant after the adjustment of radius selection. The LD around the stop A lies within the ideal value range 1 < LD < 2 mentioned in chapter 3.3, illustrating that the network density around the stop A keeps at a quite high level, and the distribution of bus lines in the transit network about the stop A is even. Meanwhile, the complexity of transit network declines rather fast in surrounding area of the stop B because the LD is in the value range 0 < LD < 1. In addition, the LD of the stop B is far smaller than that of the stop A, leading to the conclusion that the bus line design around the stop A is superior than that of the stop B in terms of the coverage of transit network. Besides, qualitative analysis is made by an observation from Fig. 3. Although the network density around the stop A is a bit lower than that of the stop B in a very small area, the bus lines around the stop A are evenly distributed in a large region excluding the small area, while the network density significantly decreases outside the small area. As a result, for the coverage homogeneity of the transit network, the region around the bus stop A is better than that of the bus stop B. Therefore, the coincidence between the analytical results of LD and qualitative analysis stands out, which means the LD indicator is able to reasonably evaluate the coverage homogeneity for urban transit network. Interestingly, based on the example, the selection of measure center and radius, namely the selection of targeted region, makes a great difference to the significance of the model and final analytical results when LD is used to make an evaluation. It is suggested the rationality of each factor concerning the model be analyzed in-depth.
5 ConclusionsIn this paper, two network structure indicators, the realistic no-linear coefficient γRNL and length dimension LD, are proposed for conventional public transit planning and management. Taking the effects of barriers in a city and topography into consideration, γRNL involves the layout of bus lines. Therefore, it is theoretically more rational than γINL in terms of evaluating the detour status of bus lines. LD is put forward to make an evaluation of the coverage homogeneity of transit networks in certain regions. It reflects the rate of change of the network density based on Fractal Theory and Differential Theory, which adds a new member to the scheme of network structure indicators for public transit. Both the validity and practicability of the two indicators get verified through an example. As for the further work concerning the two indicators, the following extensions are prospective: Firstly, the maximum reasonable value of γRNL is to be set. This critical value of γINL is 1.4 according to the document[13] and it is assumed that of γRNL is the same. In fact, there exists a little distinction between their definitions, so the critical value should be somewhat different. Secondly, the selection of measure center, radius and step length of LD are made as recommended in the literature. It does not, however, involve how to calibrate these parameters with quantitative methods in this paper, which is worth exploring their importance to the models and results of evaluation.
| [1] |
Quintero L, Sayed T, Wahba M M. Safety models incorpo-rating graph theory based transit indicators.
Accident Analysis and Prevention, 2015 (50) : 635-644.
( 0) 0)
|
| [2] |
Kumar P, Parida M, Swami M. Performance evaluation of multimodal transportation systems.
Procedia-Social and Behavior Sciences, 2013 (104) : 795-804.
( 0) 0)
|
| [3] |
Kamruzzaman M, Baker D, Washington S, et al. Advance transit oriented development typology: Case study in Brisbane.
Journal of Transport Geography, 2014 (34) : 54-70.
( 0) 0)
|
| [4] |
Hu Shujun. Study on comprehensive evaluation system of the development of urban public transit.
Transportation Science & Technology, 2004 (5) : 84-85.
( 0) 0)
|
| [5] |
Lǚ Qiang. Research concerning comprehensive evaluation indicators of urban public transit.
Heilongjiang Transport Technology, 2010 (5) : 120-121.
( 0) 0)
|
| [6] |
Li Chaokui, Cheng Liang, Li Jiangling. Evaluation of urban public transport system based on GIS: A case study of Xiangtan.
Science of Surveying and Mapping, 2010 , 35 (5) : 98-100.
( 0) 0)
|
| [7] |
Zhu Jiaxi. Study on Hierarchical Optimization Method of Public Transit Network Based on Ant Colony Glgorithm. Xi'an: Chang'an University, 2011.
( 0) 0)
|
| [8] |
Xi Jiaojiao. The Index System and Evaluation Method of Service Level for Urban Regular Transit. Jilin: Jilin University, 2013.
( 0) 0)
|
| [9] |
Kho S Y. Zigzagging of bus routes-An analytical approach.
Transportation Research Record, 2000 (1731) : 10-14.
( 0) 0)
|
| [10] |
Huang Sha, Meng Jingyu, Wang Xiaoyi. Evaluation system for public traffic in the small and medium-sized cities.
Journal of Transport Information and Safety, 2011 , 29 (1) : 32-36.
( 0) 0)
|
| [11] |
Wu Fengxia. Study on the No-linear Coefficient of the Mountain Area's Highway. Xi'an: Chang′an University, 2012.
( 0) 0)
|
| [12] |
Yang Xiaobo. Research on evaluation indicators of urban public transit network.
Science and Technology Innovation Herald, 2009 , 24 : 97-98.
( 0) 0)
|
| [13] |
GB50220-95. Code for Transport Planning on Urban Road. Beijing: Ministry of Construction of the People's Republic of China, 1995.
( 0) 0)
|
| [14] |
Tian Darui, Zhou Qinghua. A review of studies on urban planning using Fractal Theory in China.
Urban Studies, 2014 , 21 (5) : 96-101.
( 0) 0)
|
| [15] |
Hu Yanqin. The Spatial Form Study of the Urban Square Based on Fractal Theory. Dalian:Dalian University of Technology, 2012.
( 0) 0)
|
| [16] |
West G B, Brown J H, Enquist B J. The fourth dimension of life: Fractal geometry and allometric scaling of organisms. Science Reports, 1999. 1677-1679.
( 0) 0)
|
| [17] |
Wang L F, Yang X J, Baleanu D, et al. Fractal dynamical model of vehicular traffic flow within the local fractional conservation laws. Abstract and Applied Analysis, 2014. 1-5.
( 0) 0)
|
| [18] |
Sun Zhixue. Study of City Green Space System Scale Hierarchy Based on Fractal Theory. Dalian: Dalian University of Technology, 2014.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


