The mission of agile earth observation satellite is to acquire photographs of specified areas on earth surface at the requests of users with quick response[1-3]. In space on-orbit service, the inertia properties of the target satellite can be changed for some activities, so the mass characteristics parameters are often required to be estimated[4-6]. To realize the accurate control of attitude to meet some other performance, we should design a robust controller to resist the effects of external disturbances or its own modelling uncertainties. However, Keel and Bhattacharyya[7] pointed out that the traditional robust control approaches such as H∞, μ and l1 did not consider the uncertainties of controller gain.The phenomenon is common, when the controller parameter has minute adjustment at the initial running stage of system, the controller gain will have additive perturbation, and when the controller has performance degradation, the controller gain will have multiplicative perturbation[8].
The H2 technique is often used to minimize a cost function[9], while the H∞ method is used to minimize the influence of the disturbance on the performance output[10].The traditional mixed H2/H∞ control is to make the Lyapunov matrix variable with H2 constraint equal to that with H∞ constraint, so that the multi-objective integrated problem becomes a convex optimism problem with LMI constraints which brings great conservatives. To reduce the conservatives of closed-loop system, many researchers have made great contributions, Oliveira[11-12] proposed extended LMI description on the basis of discrete-time systems, and proved that by introducing auxiliary variables, the Lyapunov matrix variable can be decoupled with controller variable. Apkarian[13] used reciprocal projection theorem to give extended LMI description, but it cannot be applied in state feedback control. A mixed H2/H∞ synthesis control with regional pole placement in terms of linear matrix inequalities is also discussed in Ref.[14]. For continuous-time singular systems, Ref.[15] considered the H2 control problems with and without an H∞ constraint. Mixed H2/H∞ output-feedback controller with pole placement constraints against the uncertainties of moment of inertia and space environmental disturbances was proposed for microsatellite attitude in Ref. [16] without considering the controller perturbation. The above references indicate that most of the multi-objective problems can be solved by solving convex optimization problem with LMI constraints. However, the perturbation of controller is not taken into consideration in above references; this paper will consider the additive perturbation appearing in the initial running stage of the system.
In this paper, a mixed H2/H∞ state feedback controller of microsatellite based on extended LMI method is designed. Firstly, the H2 performance control based on extended LMI is proposed. Then, with the existing H∞ control method, we can get the mixed method which can be used in state feedback control and also decouple the Lyapunov matrix variables.We can use LMI toolbox to solve satellite attitude control problem and get parameters meeting certain conditions. For the two matrix variables are decoupled, the extended LMI method can greatly reduce the conservatives of closed-loop system. Finally, the simulations are made with the traditional LMI method and extended LMI method with and without considering the additive perturbation.
2 Problem StatementTo define a body-fixed reference frame with its origin located at the mass center of a microsatellite and with basic unit vectors being along the principal axes. The Euler's equations of motion[17-18] for the microsatellite are then given by
| $\left\{ \begin{align} & {{I}_{x}}{{{\dot{\omega }}}_{x}}+\left( {{I}_{z}}-{{I}_{y}} \right){{\omega }_{y}}{{\omega }_{z}}={{T}_{cx}}+{{T}_{gx}}+{{T}_{dx}} \\ & {{I}_{y}}{{{\dot{\omega }}}_{y}}+\left( {{I}_{x}}-{{I}_{z}} \right){{\omega }_{z}}{{\omega }_{x}}={{T}_{cy}}+{{T}_{gy}}+{{T}_{dy}} \\ & {{I}_{z}}{{{\dot{\omega }}}_{z}}+\left( {{I}_{y}}-{{I}_{x}} \right){{\omega }_{x}}{{\omega }_{y}}={{T}_{cz}}+{{T}_{gz}}+{{T}_{dz}} \\ \end{align} \right.$ | (1) |
where Ix, Iy, Iz are the principal moments of inertia; ωx, ωy, ωz are the body-axis components of angular velocity; Tij(i=c, g, d, j=x, y, z) means the external torques acting on the microsatellite including control torques Tcj, gravity gradient torque Tgj and disturbance torques Tdj.
As is known, gravity gradient torque Tgj(j=x, y, z) is easily shown as
| $ \left[ \begin{matrix} {{T}_{gx}} \\ {{T}_{gy}} \\ {{T}_{gz}} \\ \end{matrix} \right]=\left[ \begin{matrix} -3\omega _{0}^{2}\left( {{I}_{y}}-{{I}_{z}} \right)\varphi \\ -3\omega _{0}^{2}\left( {{I}_{x}}-{{I}_{z}} \right)\varphi \\ 0 \\ \end{matrix} \right] $ |
Then, Eq.(1) can be transferred into the following form:
| $\left\{ \begin{align} & {{I}_{x}}\ddot{\varphi }+4\left( {{I}_{y}}-{{I}_{z}} \right)\omega _{0}^{2}\varphi +\left( {{I}_{y}}-{{I}_{z}}-{{I}_{x}} \right){{\omega }_{0}}\dot{\psi }={{T}_{cx}}+{{T}_{dx}} \\ & {{I}_{y}}\ddot{\theta }+3\omega _{0}^{2}\left( {{I}_{x}}-{{I}_{z}} \right)\theta ={{T}_{cy}}+{{T}_{dy}} \\ & {{I}_{x}}\ddot{\psi }+\left( {{I}_{y}}-{{I}_{z}} \right)\omega _{0}^{2}\psi +\left( {{I}_{x}}+{{I}_{z}}-{{I}_{y}} \right){{\omega }_{0}}\dot{\varphi }={{T}_{cz}}+{{T}_{dz}} \\ \end{align} \right.$ | (2) |
Without considering the model uncertainties, the microsatellite attitude control system can be described by the following state space form:
| $\left\{ \begin{align} & \dot{\boldsymbol{x}}=\boldsymbol{Ax}+{{\boldsymbol{B}}_{1}}\boldsymbol{u}+{{\boldsymbol{B}}_{2}}\boldsymbol{d} \\ & {{\boldsymbol{z}}_{\infty }}={{\boldsymbol{C}}_{1}}\boldsymbol{x}+{{\boldsymbol{D}}_{1}}\boldsymbol{u}+{{\boldsymbol{D}}_{2}}\boldsymbol{d} \\ & {{\boldsymbol{z}}_{2}}={{\boldsymbol{C}}_{2}}\boldsymbol{x} \\ \end{align} \right.$ | (3) |
where, the parameters are defined as follows:State variables
The coefficient matrices are defined as follows:
| $ \boldsymbol{A} = \left[ {\begin{array}{*{20}{c}} 0&0&0&1&0&0 \\ 0&0&0&0&1&0 \\ 0&0&0&0&0&1 \\ { - 4\omega _0^2I_x^{ - 1}\left( {{I_y} - {I_z}} \right)}&0&0&0&0&{ - {\omega _0}I_x^{ - 1}\left( {{I_y} - {I_x} - {I_z}} \right)} \\ 0&{ - 3\omega _0^2I_y^{ - 1}\left( {{I_x} - {I_z}} \right)}&0&0&0&0 \\ 0&0&{ - \omega _0^2I_z^{ - 1}\left( {{I_y} - {I_x}} \right)}&{{\omega _0}I_z^{ - 1}\left( {{I_y} - {I_x} - {I_z}} \right)}&0&0 \end{array}} \right] $ |
| $ \begin{gathered} {\boldsymbol{B}_1} = {\boldsymbol{B}_2} = {\left[ {{0_{3 \times 3}}\;\;\;{\text{diag}}\left( {I_x^{ - 1},I_y^{ - 1},I_z^{ - 1}} \right)} \right]^{\text{T}}},{\boldsymbol{C}_2} = \left[ {{\boldsymbol{I}_{3 \times 3}}\;\;{0_{3 \times 3}}} \right],{\boldsymbol{D}_1} = {\boldsymbol{D}_2} = {10^{ - 3}} \times {\boldsymbol{I}_{3 \times 3}} \hfill \\ {\boldsymbol{C}_1} = {10^{ - 3}}\left[ {\begin{array}{*{20}{c}} { - 4\omega _0^2\left( {{I_y} - {I_z}} \right)}&0&0&0&0&{ - {\omega _0}\left( {{I_y} - {I_x} - {I_z}} \right)} \\ 0&{ - 3\omega _0^2\left( {{I_x} - {I_z}} \right)}&0&0&0&0 \\ 0&0&{ - \omega _0^2\left( {{I_y} - {I_x}} \right)}&{{\omega _0}\left( {{I_y} - {I_x} - {I_z}} \right)}&0&0 \end{array}} \right] \hfill \\ \end{gathered} $ |
As to Eq.(3), design state feedback controller
| $\boldsymbol{u} = \boldsymbol{Kx}$ | (4) |
Then, the closed-loop attitude control system of satellite becomes
| $\left\{ \begin{gathered} \mathit{\dot x} = \left( {\boldsymbol{A} + {\boldsymbol{B}_1}\boldsymbol{K}} \right)\boldsymbol{x} + {\boldsymbol{B}_2}\boldsymbol{d} \hfill \\ {\boldsymbol{z}_\infty } = \left( {{\boldsymbol{C}_1} + {\boldsymbol{D}_1}\boldsymbol{K}} \right)\boldsymbol{x} + {\boldsymbol{D}_2}\boldsymbol{d} \hfill \\ {\boldsymbol{z}_2} = {\boldsymbol{C}_2}x \hfill \\ \end{gathered} \right.$ | (5) |
With some possibly small γ∞ and γ2, which both imply the minimal attenuation level, the designed controller can satisfy the following H∞ and H2 performance constraint.
| $\begin{gathered} {\left\| {{\boldsymbol{G}_{{z_\infty }d}}} \right\|_\infty } = \hfill \\ {\left\| {\left( {{\boldsymbol{C}_1} + {\boldsymbol{D}_1}\boldsymbol{K}} \right){{\left( {\boldsymbol{sI} - \left( {\boldsymbol{A} + {\boldsymbol{B}_1}\boldsymbol{K}} \right)} \right)}^{ - 1}}{\boldsymbol{B}_2} + {\boldsymbol{D}_2}} \right\|_\infty } \leqslant {\gamma _\infty } \hfill \\ \end{gathered} $ | (6) |
| ${\left\| {{\boldsymbol{G}_{{z_2}d}}} \right\|_2} = {\left\| {{\boldsymbol{C}_2}{{\left( {\boldsymbol{sI} - \left( {\boldsymbol{A} + {\boldsymbol{B}_1}\boldsymbol{K}} \right)} \right)}^{ - 1}}{\boldsymbol{B}_2}} \right\|_2} \leqslant {\gamma _2}$ | (7) |
where, Eq.(6) denotes that the upper bound of H∞ norm of the transfer function matrix corresponding to the output vector z∞ is γ∞, and Eq.(7) denotes that the upper bound of H2 norm of the transfer function matrix corresponding to the output vector z2 is γ2, respectively.
Definition 1 The H∞ norm definition of transfer function Gz∞d is
| $ {\left\| {{G_{{z_\infty }d}}\left( s \right)} \right\|_\infty } = \mathop {\sup }\limits_\omega {\sigma _{\max }}\left( {{G_{{z_\infty }d}}\left( {j\omega } \right)} \right) $ |
Definition 2 The H2 norm definition of transfer function Gz2d is
| $ \begin{align} & {{\left\| {{\boldsymbol{G}}_{{{z}_{2}}d}}\left( s \right) \right\|}_{2}}= \\ & \text{Trace}{{\left[ \left( 1/\left( 2\text{ }\!\!\pi\!\!\text{ } \right) \right)\int_{-\infty }^{+\infty }{{{\boldsymbol{G}}_{{{z}_{2}}d}}\left( j\omega \right)\cdot \boldsymbol{G}_{{{z}_{2}}d}^{*}\left( j\omega \right)d\omega } \right]}^{1/2}} \\ \end{align} $ |
The mixed H2/H∞ problem can be stated as follow:
For a given positive scalar γ∞, to obtain the state feedback gain matrix K, so that the satellite closed-loop attitude control system is stable and with the constraint
Lemma 1[19] For a given scalar γ∞, the closed-loop system is stable and satisfies Eq.(6), if and only if there exist matrix W and symmetric positive definite matrix X, such that
| $\left[ \begin{matrix} \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{W}+{{\left( \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{W} \right)}^{\text{T}}} & {{\boldsymbol{B}}_{2}} & {{\left( {{\boldsymbol{C}}_{1}}\boldsymbol{X}+{{\boldsymbol{D}}_{1}}\boldsymbol{W} \right)}^{\text{T}}} \\ \boldsymbol{B}_{2}^{\text{T}} & -{{\mathit{\gamma} }_{\infty }}\boldsymbol{I} & \boldsymbol{D}_{2}^{\text{T}} \\ {{\boldsymbol{C}}_{1}}\boldsymbol{X}+{{\boldsymbol{D}}_{1}}\boldsymbol{W} & {{\boldsymbol{D}}_{2}} & -{{\mathit{\gamma} }_{\infty }}\boldsymbol{I} \\ \end{matrix} \right]<0$ | (8) |
Lemma 2 For a given scalar γ2, the closed-loop system is stable and satisfies Eq.(7), if and only if there exist matrix Q, symmetric matrix Z and symmetric positive definite matrix X, such that
| $\left\{ \begin{align} & \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{Q}+{{\left( \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{Q} \right)}^{\text{T}}}+{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}<0 \\ & \left[ \begin{matrix} -\boldsymbol{Z} & {{\boldsymbol{C}}_{2}}X \\ {{\left( {{\boldsymbol{C}}_{2}}\boldsymbol{X} \right)}^{\text{T}}} & -\boldsymbol{X} \\ \end{matrix} \right]<0 \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\rho \\ \end{align} \right.$ | (9) |
Proof From Ref. [19], we can know the following statements are equivalent:
(1) ∃x∈Rn, such that Trace (A(x)) < γ;
(2) ∃x∈Rn, Z∈Sm, such that A(x) < Z, while Trace (Z) < γ.
For general transfer function matrix, H2 norm condition ‖C(sI-A)-1B‖2≤γ holds if and only if ∃X>0, the following LMI is satisfied.
| $ \boldsymbol{AX}+\boldsymbol{X}{{\boldsymbol{A}}^{\text{T}}}+\boldsymbol{B}{{\boldsymbol{B}}^{\text{T}}}<0,\text{Trace}\left( \boldsymbol{CX}{{\boldsymbol{C}}^{\text{T}}} \right)<{{\gamma }^{2}} $ |
Then, Eq.(7) holds if and only if there exists a symmetric positive definite matrix X, such that
| $ \left\{ \begin{align} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{X}+\boldsymbol{X}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}<0, \\ & \text{Trace}\left( {{\boldsymbol{C}}_{2}}\boldsymbol{X}\boldsymbol{C}_{2}^{\text{T}} \right)<\gamma _{2}^{2} \\ \end{align} \right. $ |
According to the equivalent statements, we can have
| $ \left\{ \begin{align} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{X}+\boldsymbol{X}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}<0, \\ & {{\boldsymbol{C}}_{2}}\boldsymbol{X}\boldsymbol{C}_{2}^{\text{T}}<Z \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\gamma _{2}^{2} \\ \end{align} \right. $ |
where Z is some symmetric matrix.
Using Schur complement lemma, we can get
| $ \left\{ \begin{align} & \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{Q}+{{\left( \boldsymbol{AX}+{{\boldsymbol{B}}_{1}}\boldsymbol{Q} \right)}^{\text{T}}}+{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}<0 \\ & \left[ \begin{matrix} -\boldsymbol{Z} & {{\boldsymbol{C}}_{2}}X \\ {{\left( {{\boldsymbol{C}}_{2}}\boldsymbol{X} \right)}^{\text{T}}} & -\boldsymbol{X} \\ \end{matrix} \right]<0 \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\rho \\ \end{align} \right. $ |
where, ρ=γ22, Q=KX. Namely, Lemma 2 is proved.
In Ref.[20], the solution of mixed H2/H∞ control system used Lemma 1 and Lemma 2. Then, the LMI toolbox can be used to obtain the state feedback gain K, but condition W=Q is required, which brings certain conservatives. In order to reduce the conservatives, we need to get rid of the restriction that the two matrices are equal.
For the additive perturbation of controller will appear when the controller parameter has minute adjustment at the initial running stage of system, the designed controller should guarantee the stability of the closed-loop system when ΔK exists. Where, ΔK means additive perturbation with the following form[18].
| $\mathit{\Delta} \boldsymbol{K}=\tilde{\boldsymbol{M}}\tilde{\boldsymbol{F}}\left( t \right)\tilde{\boldsymbol{N}},\tilde{\boldsymbol{F}}{{\left( t \right)}^{\text{T}}}\tilde{\boldsymbol{F}}\left( t \right)\le \boldsymbol{I}$ | (10) |
where, M and N are two constant real matrices with appropriate dimension; F(t) is unknown matrix containing Lebesgue measure elements.
Namely, when the actual state feedback controller
| $\boldsymbol{u}\left( t \right)=\left( \boldsymbol{K}+\mathit{\Delta} \boldsymbol{K} \right)\boldsymbol{x}\left( t \right)$ | (11) |
the satellite attitude control system should also be stable with quick response.
3 Mixed H2/H∞ State Feedback Attitude ControlBefore introducing theorem 1, Schur complement lemma and reciprocal projection lemma are described first.
Lemma 3 (Schur complement lemma) Let the partitioned matrix
| $ \boldsymbol{A}=\left[ \begin{matrix} {{\boldsymbol{A}}_{11}} & {{\boldsymbol{A}}_{12}} \\ \boldsymbol{A}_{12}^{\text{T}} & {{\boldsymbol{A}}_{22}} \\ \end{matrix} \right] $ |
be symmetric. Then
| $\begin{align} & \boldsymbol{A}<0\Leftrightarrow {{\boldsymbol{A}}_{11}}<0{{\boldsymbol{A}}_{12}}-\boldsymbol{A}_{12}^{\text{T}}\boldsymbol{A}_{11}^{-1}{{\boldsymbol{A}}_{12}}<0\Leftrightarrow \\ & {{\boldsymbol{A}}_{22}}<0{{\boldsymbol{A}}_{11}}-{{\boldsymbol{A}}_{12}}\boldsymbol{A}_{22}^{-1}\boldsymbol{A}_{12}^{\text{T}}<0 \\ \end{align}$ | (12) |
or
| $\begin{align} & \boldsymbol{A}>0\Leftrightarrow {{\boldsymbol{A}}_{11}}>0{{\boldsymbol{A}}_{12}}-\boldsymbol{A}_{12}^{\text{T}}\boldsymbol{A}_{11}^{-1}{{\boldsymbol{A}}_{12}}>0\Leftrightarrow \\ & {{\boldsymbol{A}}_{22}}>0{{\boldsymbol{A}}_{11}}-{{\boldsymbol{A}}_{12}}\boldsymbol{A}_{22}^{-1}\boldsymbol{A}_{12}^{\text{T}}>0 \\ \end{align}$ | (13) |
Lemma 4[13] (Reciprocal projection lemma) Let P be any given positive definite matrix. The following statements are equivalent:
(1)LMI
| $\mathit{\Psi} +\boldsymbol{S}+{{\boldsymbol{S}}^{\text{T}}}<0$ | (14) |
(2)The LMI problem
| $\left[ \begin{align} & \mathbf{\Psi }+\boldsymbol{P}-\boldsymbol{W}-{{\boldsymbol{W}}^{\text{T}}}\ \ \ {{\boldsymbol{S}}^{\text{T}}}+{{\boldsymbol{W}}^{\text{T}}} \\ & \boldsymbol{S}+\boldsymbol{W}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ -\boldsymbol{P} \\ \end{align} \right]<0$ | (15) |
is feasible with respect to W.
Considering the system described by the first and third equations in Eq.(5), the H2 performance can be described by theorem 1.
Theorem 1 For a given scalar γ2, the closed-loop system is stable and satisfies Eq.(7), if and only if there exist matrices N1=XB1K, N2=QTB1K, N3=B1KQ, Q, symmetric matrix Z and symmetric positive definite matrix X, such that
(i)(A+B1K) is stable and
| $ \begin{align} & {{\left\| {{\boldsymbol{C}}_{2}}{{\left( \boldsymbol{sI}-\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right) \right)}^{-1}}{{\boldsymbol{B}}_{2}} \right\|}_{2}}\le {{\gamma }_{2}} \\ & \left( \text{ii} \right)\left[ \begin{matrix} {{\left( \boldsymbol{X}\boldsymbol{A}+{{\boldsymbol{N}}_{1}} \right)}^{\text{T}}}+\left( \boldsymbol{X}\boldsymbol{A}+{{\boldsymbol{N}}_{1}} \right) & \boldsymbol{X}{{\boldsymbol{B}}_{2}} \\ \boldsymbol{B}_{2}^{\text{T}}\boldsymbol{X} & -\boldsymbol{I} \\ \end{matrix} \right]<0 \\ & \left[ \begin{matrix} \boldsymbol{X} & \boldsymbol{C}_{2}^{\text{T}} \\ {{\boldsymbol{C}}_{2}} & \boldsymbol{Z} \\ \end{matrix} \right]>0 \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\gamma _{2}^{2} \\ \end{align} $ |
| $ \begin{align} & \left( \text{iii} \right)\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & \left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{N}}_{2}} \right)+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}{{\boldsymbol{B}}_{2}} & {{\boldsymbol{Q}}^{\text{T}}} \\ {{\left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{N}}_{2}} \right)}^{\text{T}}}+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0 \\ & \left[ \begin{matrix} \boldsymbol{X} & \boldsymbol{C}_{2}^{\text{T}} \\ {{\boldsymbol{C}}_{2}} & \boldsymbol{Z} \\ \end{matrix} \right]>0 \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\gamma _{2}^{2} \\ \end{align} $ |
| $ \begin{align} & \left( \text{iv} \right)\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & {{\left( \boldsymbol{A}\boldsymbol{Q}+{{\boldsymbol{N}}_{3}} \right)}^{\text{T}}}+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{C}_{2}^{\text{T}} & {{\boldsymbol{Q}}^{\text{T}}} \\ \left( \boldsymbol{A}\boldsymbol{Q}+{{\boldsymbol{N}}_{3}} \right)+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ {{\boldsymbol{C}}_{2}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0 \\ & \left[ \begin{matrix} \boldsymbol{X} & \boldsymbol{B}_{2}^{\text{T}} \\ {{\boldsymbol{B}}_{2}} & \boldsymbol{Z} \\ \end{matrix} \right]>0 \\ & \text{Trace}\left( \boldsymbol{Z} \right)<\gamma _{2}^{2} \\ \end{align} $ |
Statements(i)(ii)(iii)(iv) are equivalent.
Proof The equivalence of (i) and (ii) is standard, so we only need to prove the equivalence of (ii)(iii)(iv).
First, the equivalence of(ii)(iii) is proved.
With Schur complement lemma, the first LMI in (ii) can be written as
| ${{\left( \boldsymbol{X}\boldsymbol{A}+{{\boldsymbol{\boldsymbol{N}}}_{1}} \right)}^{\text{T}}}+\left( \boldsymbol{X}\boldsymbol{A}+{{\boldsymbol{\boldsymbol{N}}}_{1}} \right)+\gamma _{2}^{-1}\boldsymbol{X}{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}\boldsymbol{X}<0$ | (16) |
For N1=XB1K, Eq.(16) can be translated into
| ${{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}\boldsymbol{X}+\boldsymbol{X}\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)+\boldsymbol{X}{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}\boldsymbol{X}<0$ | (17) |
Let Y=X-1, Y is also symmetric positive definite matrix, by performing the congruence transformation,
| $\begin{align} & {{\boldsymbol{Y}}^{\text{T}}}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}\boldsymbol{X}\boldsymbol{Y}+{{\boldsymbol{Y}}^{\text{T}}}\boldsymbol{X}\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+ \\ & {{\boldsymbol{Y}}^{\text{T}}}\boldsymbol{X}{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}\boldsymbol{X}\boldsymbol{Y}<0 \\ \end{align}$ | (18) |
With X=XT, Y=YT, Y=X-1, we have
| $\boldsymbol{Y}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+{{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}<0$ | (19) |
With Lemma 4 (Reciprocal projection lemma), if S=Y (A+B1K)T, Ψ=B2B2T, Eq.(19) is equivalent with Eq.(20),
| $\left[ \begin{matrix} {{\boldsymbol{B}}_{2}}\boldsymbol{B}_{2}^{\text{T}}+\boldsymbol{P}-\boldsymbol{W}-{{\boldsymbol{W}}^{\text{T}}} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+{{\boldsymbol{W}}^{\text{T}}} \\ \boldsymbol{Y}\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)+\boldsymbol{W} & -\boldsymbol{P} \\ \end{matrix} \right]<0$ | (20) |
With Schur complement lemma, Eq.(20) can be converted into
| $\left[ \begin{matrix} \boldsymbol{P}-\boldsymbol{W}-{{\boldsymbol{W}}^{\text{T}}} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+{{\boldsymbol{W}}^{\text{T}}} & {{\boldsymbol{B}}_{2}} \\ \boldsymbol{Y}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+\boldsymbol{W} & -\boldsymbol{P} & 0 \\ \boldsymbol{B}_{2}^{\text{T}} & 0 & -\boldsymbol{I} \\ \end{matrix} \right]<0$ | (21) |
With Schur complement lemma again, we can obtain
| $\left[ \begin{matrix} -\boldsymbol{W}-{{\boldsymbol{W}}^{\text{T}}} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+{{\boldsymbol{W}}^{\text{T}}} & {{\boldsymbol{B}}_{2}} & \boldsymbol{P} \\ \boldsymbol{Y}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+\boldsymbol{W} & -\boldsymbol{P} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{P} & 0 & 0 & -\boldsymbol{P} \\ \end{matrix} \right]<0$ | (22) |
Similarly, let P=X-1, Q=W-1, by performing the congruence transformation, namely, multiplied by a matrix on both sides of Eq.(22) with MT and M, where
| $\boldsymbol{M}=\left[ \begin{matrix} \boldsymbol{Q} & 0 & 0 & 0 \\ 0 & \boldsymbol{X} & 0 & 0 \\ 0 & 0 & \boldsymbol{I} & 0 \\ 0 & 0 & 0 & \boldsymbol{X} \\ \end{matrix} \right]$ | (23) |
Then,
| ${{\boldsymbol{M}}^{\text{T}}}\left[ \begin{matrix} -\boldsymbol{W}-{{\boldsymbol{W}}^{\text{T}}} & \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Y}+{{\boldsymbol{W}}^{\text{T}}} & {{\boldsymbol{B}}_{2}} & \boldsymbol{P} \\ \boldsymbol{Y}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+\boldsymbol{W} & -\boldsymbol{P} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{P} & 0 & 0 & -\boldsymbol{P} \\ \end{matrix} \right]\boldsymbol{M}<0$ | (24) |
We can get
| $\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & {{\boldsymbol{Q}}^{\text{T}}}\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}{{\boldsymbol{B}}_{2}} & {{\boldsymbol{Q}}^{\text{T}}} \\ {{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}\boldsymbol{Q}+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0$ | (25) |
For N2=QTB1K, then,
| $\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & \left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{\boldsymbol{N}}}_{2}} \right)+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}{{\boldsymbol{B}}_{2}} & {{\boldsymbol{Q}}^{\text{T}}} \\ {{\left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{\boldsymbol{N}}}_{2}} \right)}^{\text{T}}}+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0$ | (26) |
It can be seen that the first LMI in(iii) is concluded, and the last two is the same with that of (ii). Next, we will prove the equivalence of (iii) and (iv).
Because system S1(A+B1K), B2, C2
| $\left\{ \begin{align} & \dot{x}=\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{x}+{{\boldsymbol{B}}_{2}}\boldsymbol{d} \\ & {{\boldsymbol{z}}_{2}}={{\boldsymbol{C}}_{2}}\boldsymbol{x} \\ \end{align} \right.$ | (27) |
and system S2(A+B1K)T, C2T, B2T
| $\left\{ \begin{align} & \dot{x}={{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}\boldsymbol{x}+\boldsymbol{C}_{2}^{\text{T}}\boldsymbol{d} \\ & {{\boldsymbol{z}}_{2}}=\boldsymbol{B}_{2}^{\text{T}}\boldsymbol{x} \\ \end{align} \right.$ | (28) |
are dual systems, with transformation ((A+B1K), B2, C2)→((A+B1K)T, C2T, B2T), Eq.(25) can be turned into
| $\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & {{\boldsymbol{Q}}^{\text{T}}}{{\left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)}^{\text{T}}}+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{C}_{2}^{\text{T}} & {{\boldsymbol{Q}}^{\text{T}}} \\ \left( \boldsymbol{A}+{{\boldsymbol{B}}_{1}}\boldsymbol{K} \right)\boldsymbol{Q}+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ {{\boldsymbol{C}}_{2}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0$ | (29) |
For N3=B1KQ, Eq.(29) can yield
| $\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & {{\left( \boldsymbol{A}\boldsymbol{Q}+{{\boldsymbol{\boldsymbol{N}}}_{3}} \right)}^{\text{T}}}+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{C}_{2}^{\text{T}} & {{\boldsymbol{Q}}^{\text{T}}} \\ \left( \boldsymbol{A}\boldsymbol{Q}+{{\boldsymbol{\boldsymbol{N}}}_{3}} \right)+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ {{\boldsymbol{C}}_{2}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0$ | (30) |
Similarly, the last two LMIs in(iv) can be obtained with transformation ((A+B1K), B2, C2)→((A+B1K)T, C2T, B2T).
Based on lemma 1 and theorem 1, we can get the following theorem that can solve the mixed H2/H∞ problem. Here, take the third statement in theorem 1 for example.
Theorem 2 For system represented by Eq.(5), the following optimization problem
| $\text{s}\text{.t}\text{.}\left[ \begin{matrix} -\boldsymbol{Q}-{{\boldsymbol{Q}}^{\text{T}}} & \left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{N}}_{2}} \right)+\boldsymbol{X} & {{\boldsymbol{Q}}^{\text{T}}}{{\boldsymbol{B}}_{2}} & {{\boldsymbol{Q}}^{\text{T}}} \\ {{\left( {{\boldsymbol{Q}}^{\text{T}}}\boldsymbol{A}+{{\boldsymbol{N}}_{2}} \right)}^{\text{T}}}+\boldsymbol{X} & -\boldsymbol{X} & 0 & 0 \\ \boldsymbol{B}_{2}^{\text{T}}\boldsymbol{Q} & 0 & -\boldsymbol{I} & 0 \\ \boldsymbol{Q} & 0 & 0 & -\boldsymbol{X} \\ \end{matrix} \right]<0 $ |
| $ \left[ \begin{matrix} \boldsymbol{X} & \boldsymbol{C}_{2}^{\text{T}} \\ {{\boldsymbol{C}}_{2}} & \boldsymbol{Z} \\ \end{matrix} \right]>0;Trace\left( \boldsymbol{Z} \right)<\rho ;\boldsymbol{X}>0;{{\gamma }_{2}}>0 $ |
| $ \left[ \begin{matrix} \boldsymbol{A}\boldsymbol{X}+{{\boldsymbol{B}}_{1}}\boldsymbol{W}+{{\left( \boldsymbol{A}\boldsymbol{X}+{{\boldsymbol{B}}_{1}}\boldsymbol{W} \right)}^{\text{T}}} & {{\boldsymbol{B}}_{2}} & {{\left( {{\boldsymbol{C}}_{1}}\boldsymbol{X}+{{\boldsymbol{D}}_{1}}\boldsymbol{W} \right)}^{\text{T}}} \\ \boldsymbol{B}_{2}^{\text{T}} & -{{\gamma }_{\infty }}\boldsymbol{I} & \boldsymbol{D}_{2}^{\text{T}} \\ {{\boldsymbol{C}}_{1}}\boldsymbol{X}+{{\boldsymbol{D}}_{1}}\boldsymbol{W} & {{\boldsymbol{D}}_{2}} & -{{\gamma }_{\infty }}\boldsymbol{I} \\ \end{matrix} \right] $ |
Where ρ=γ22, when the LMIs are feasible, the state feedback gain matrix can be constructed as K=WX-1.
From the above LMIs, we can see the Lyapunov matrix variables Q and W are not the same, only make restriction on the additional variables to reduce conservatives.
4 Simulation and AnalysisLet
Ix=20 kg·m2, Iy=15 kg·m2, Iz=12 kg·m2
Choose the initial state as
x(0)=[0.1 0.1 0.1 0.02 0.02 0.02]T
where, the unit of angle is (rad) and the unit of angular velocity is (rad/s). Meanwhile d is chosen as
| $ \boldsymbol{d}={{10}^{-5}}\left[ \begin{align} & \sin \left( \omega t \right) \\ & \sin \left( \omega t+\text{ }\!\!\pi\!\!\text{ }/4 \right) \\ & \sin \left( \omega t+\text{ }\!\!\pi\!\!\text{ }/2 \right) \\ \end{align} \right]\text{N }\!\!\times\!\!\text{ m} $ |
ΔK is determined by
| $ \begin{align} & \tilde{\boldsymbol{M}}=\left[ 1;1;1 \right],\tilde{\boldsymbol{F}}\left( t \right)=\sin \left( 100{{\omega }_{0}}t+\text{ }\!\!\pi\!\!\text{ }/4 \right) \\ & \tilde{\boldsymbol{N}}=\left[ 0.1\ \ 0.01\ \ 0.1\ \ 0.01\ \ 0.1\ \ 0.01 \right] \\ \end{align} $ |
where ω0 means the orbital angular velocity with the height of 300 km.
First of all, the additive perturbation ΔK is not taken into consideration, and simulations are made to show the two methods based on traditional LMI and extended LMI can both guarantee the stability of microsatellite attitude system.
With the proposed method in this paper, the controller gain can be obtained as
| $ \boldsymbol{K}=\left[ \begin{matrix} -2.2855 & 0 & 0.0042 & -9.7489 & 0 & 0.0013 \\ 0 & -2.0024 & 0 & 0 & -8.1134 & 0 \\ -0.0030 & 0 & -1.8009 & 0.0012 & 0 & -7.0465 \\ \end{matrix} \right] $ |
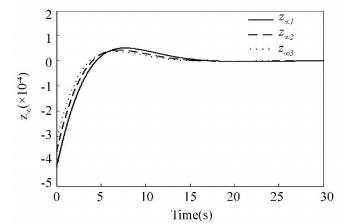
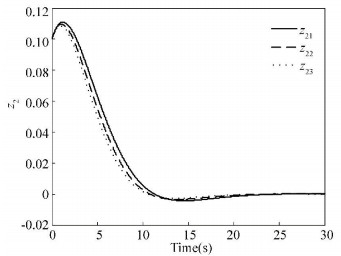
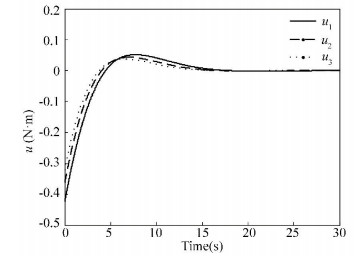
The output of z∞ and z2 can be seen in Fig. 1 and Fig. 2, and the corresponding control torques are shown in Fig. 3.
|
Figure 1 Output of z∞ based on extended LMI |
|
Figure 2 Output of z2 based on extended LMI |
|
Figure 3 Control torques based on extended LMI |
To make comparisons, Lemma 1 and Lemma 2 are applied in the closed-loop attitude control system, and then we have
| $ \boldsymbol{K}=\left[ \begin{matrix} -0.0150 & 0 & 0 & -0.9854 & 0 & -0.0197 \\ 0 & -0.0122 & 0 & 0 & -0.7794 & 0 \\ 0 & 0 & -0.0131 & 0.0197 & 0 & -0.7195 \\ \end{matrix} \right] $ |
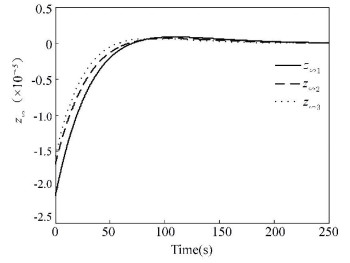
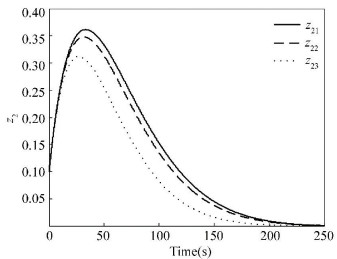
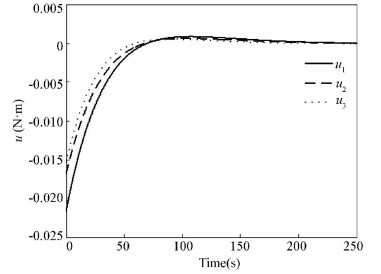
The output of z∞ and z2 can be seen in Figs. 4 and 5, and the corresponding control torques are shown in Fig. 6.
|
Figure 4 Output of z∞ based on traditional LMI |
|
Figure 5 Output of z2 based on traditional LMI |
|
Figure 6 Control torques based on traditional LMI |
Comparing Figs. 1-3 with Figs. 4-6, it can be seen obviously that with the mixed H2/H∞ controlapproach based on extended LMI, the satellite attitude control system can become stable within 20 s which is much shorter than 200 s of the traditional LMI method. From Figs. 2 and 5, we can see the extended LMI method can get a smaller H2 norm, which means a better performance.
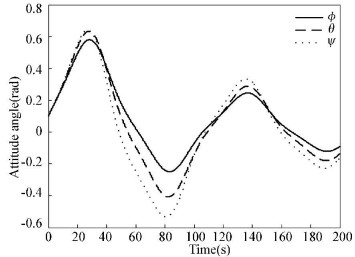
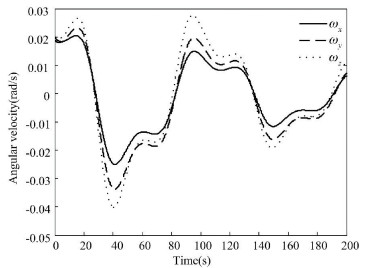
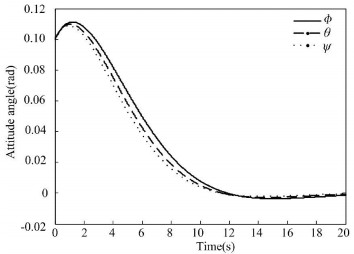
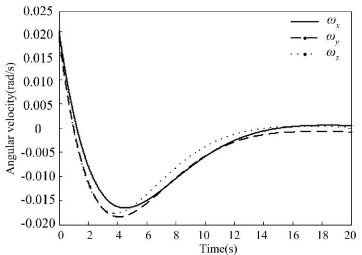
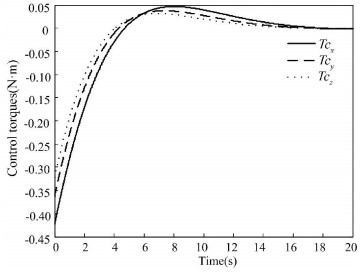
To describe the effect of additive perturbation on closed-loop attitude system and show the superiority of the proposed method, additive perturbation ΔK is added into controller gain. Then, the simulation results of traditional LMI method and extended LMI method can be seen in Figs. 7-9 and Figs. 10-12, respectively. Figs. 7-9 show that the traditional LMI method will make the final closed-loop system state diffuse while the extended LMI method can still guarantee the stability of closed-loop attitude system within 20 s.
|
Figure 7 Attitude angle based on traditional LMI |
|
Figure 8 Angular velocity based on traditional LMI |
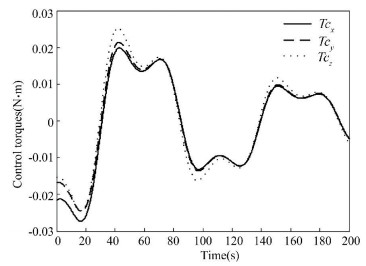
|
Figure 9 Control torques based on traditional LMI |
|
Figure 10 Attitude angle based on extended LMI |
|
Figure 11 Angular velocity based on extended LMI |
|
Figure 12 Control torques based on extended LMI |
5 Conclusions
The controllers designedby mixed H2/H∞ method can both suppress external disturbance and make the satellite attitude control system have better control performance. With the new mixed H2/H∞ method based on extended LMI, the state feedback controller of microsatellite attitude system can be obtained, which solves the restriction of traditional single Lyapunov variable and reduces the system conservatives and makes the microsatellite attitude control system response much more quickly. Furthermore, at the initial running stage of the system, once the additive perturbation of controller exists, the extended LMI method proposed in this paper can still guarantee the stability of microsatellite attitude control system with quick response while the traditional mixed H2/H∞ control method will make attitude system diffuse.
| [1] |
Sun Kai, Yang Zhengyu, Wang Pei, et al. Mission planning and action planning for agile earth-observing satellite with genetic algorithm.
Journal of Harbin Institute of Technology(New Series), 2013 , 20 (5) : 51-56.
( 0) 0)
|
| [2] |
Tangpattanakul P, Jozefowiez N, Lopez P. A multi-objective local search heuristic for scheduling Earth observations taken by an agile satellite.
European Journal of Operational Research, 2015 , 245 (2) : 542-554.
DOI:10.1016/j.ejor.2015.03.011 ( 0) 0)
|
| [3] |
Lemaître M, Verfaillie G, Jouhaud F. Selecting and scheduling observations of agile satellites.
Aerospace Science and Technology, 2002 , 6 (5) : 367-381.
DOI:10.1016/S1270-9638(02)01173-2 ( 0) 0)
|
| [4] |
Liu Chuang, Wang Feng. In-orbit estimation of inertia parameters of target satellite after capturing the tracking satellite. Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA). Piscataway: IEEE, 2014. 3940-3945.
( 0) 0)
|
| [5] |
Xia Xiwang, Jing Wuxing, Gao Changsheng, et al. Attitude control of spacecraft during propulsion of swing thruster.
Journal of Harbin Institute of Technology(New Series), 2012 , 19 (1) : 94-100.
( 0) 0)
|
| [6] |
Liu Chuang, Shi Keke, Wang Feng. Mass and mass center identification of target satellite after rendezvous and docking. Proceedings of the 11th World Congress on Intelligent Control and Automation (WCICA). Piscataway: IEEE, 2014. 5802-5807.
( 0) 0)
|
| [7] |
Keel L H, Bhattacharyya S P. Robust, fragile, or optimal?.
IEEE Transactions on Automatic Control, 1997 , 42 (8) : 1098-1105.
DOI:10.1109/9.618239 ( 0) 0)
|
| [8] |
Guan Xinping, Zhang Qunliang, Long Chengnian. Resilient guaranteed cost control for a class of 2-D uncertain discrete systems.
Control Theory & Applications, 2004 , 21 (1) : 125-128.
( 0) 0)
|
| [9] |
Ban Y S, Varatharajoo R, Ovchinnikov M. H2 optimal control solution for a combined energy and attitude control system.
Acta Astronautica, 2012 , 76 : 79-83.
DOI:10.1016/j.actaastro.2012.02.013 ( 0) 0)
|
| [10] |
Wang Mao, Zhou Zhenhua, Liang Tiantian. Robust H∞ and H2 static output feedback control of discrete-time piecewise affine singular systems with norm-bounded uncertainties.
Journal of Harbin Institute of Technology(New Series), 2014 , 21 (3) : 1-8.
( 0) 0)
|
| [11] |
De Oliveira M C, Bernussou J, Geromel J C. A new discrete-time robust stability condition.
Systems & Control letters, 1999 , 37 (4) : 261-265.
DOI:10.1016/S0167-6911(99)00035-3 ( 0) 0)
|
| [12] |
De Oliveira M C, Geromel J C, Bernussou J. Extended H2 and H norm characterizations and controller parametrizations for discrete-time systems.
International Journal of Control, 2002 , 75 (9) : 666-679.
DOI:10.1080/00207170210140212 ( 0) 0)
|
| [13] |
Apkarian P, Tuan H D, Bernussou J.Analysis, eigenstructure assignment and H2 multichannel synthesis with enhanced LMI characterizations. Proceedings of the 39th IEEE Conference on Decision and Control. Piscataway: IEEE, 2000. 1489-1494.
( 0) 0)
|
| [14] |
Chilali M, Gahinet P. H∞ design with pole placement constraints: an LMI approach.
IEEE Transactions on Automatic Control, 1996 , 41 (3) : 358-367.
DOI:10.1109/9.486637 ( 0) 0)
|
| [15] |
Zhang Liqian, Huang Biao, Lam J. LMI synthesis of H2 and mixed H2/H∞ controllers for singular systems.
IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, 2003 , 50 (9) : 615-626.
DOI:10.1109/TCSII.2003.816904 ( 0) 0)
|
| [16] |
WuBaolin, Cao Xibin, Li Zhengxue. Multi-objective output-feedback control for microsatellite attitude control: An LMI approach.
Acta Astronautica, 2009 , 64 (11) : 1021-1031.
DOI:10.1016/j.actaastro.2008.12.012 ( 0) 0)
|
| [17] |
Yang Cianndong, Sun Yunping. Mixed H2/H∞ state-feedback design for microsatellite attitude control.
Control Engineering Practice, 2002 , 10 (9) : 951-970.
DOI:10.1016/S0967-0661(02)00049-7 ( 0) 0)
|
| [18] |
Liu Chuang, Wang Feng, Shi Keke, et al. Robust H∞ control for satellite attitude control system with uncertainties and additive perturbation.
International Journal of Science, 2014 , 1 (2) : 1-9.
( 0) 0)
|
| [19] |
Duan Guangren, Yu Haihua. LMIs in Control Systems:Analysis, Design and Applications. Boca Raton:CRC Press, 2013.
( 0) 0)
|
| [20] |
Liu Chuang, Sun Zhaowei, Shi Keke, et al. Mixed H2/H∞Control approach and its application in satellite attitude control system.
International Journal of Engineering Research in Africa, 2016 , 25 : 89-97.
DOI:10.4028/www.scientific.net/JERA.25 ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


