2. College of Computer, Nanjing University of Posts and Telecommunications, Nanjing 210003, China ;
3. State Key Laboratory of Information Security (Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
At the inspiration of Zheng's public key signcryption idea[1] and with the purpose to meet the need of network multicast, a large number of multi-receiver signcryption schemes are proposed. Typically, Baek et al.[2] designed multi-receiver signcryption scheme based on identity. Elkamchouchi and Abouelseoud[3] constructed a publicly verifiable multi-receiver signcryption scheme based on identity, which meets the need of the firewall or gateway to verify the identity of the sender. Lal and Kushwah[4] designed multi-receiver signcryption scheme based on identity in which the sender is anonymous.Recently, a number of new signcryption schemes have also been put forward[5-6].
The schemes described above are designed mainly at the basis of the bilinear, and the length of the ciphertext and the number of the receivers are linear, so the ciphertext is expanding quickly with the number of receivers increasing. Meanwhile, the bilinear problem has been solved by polynomial time quantum algorithm[7]. Thus, in the post quantum era, we have to design a multi-receiver signcryption scheme based on new assumption.
Maybe extending bilinear to multilinear is one of the solutions. In 2003, Boneh and Silverberg[8] proposed the idea of designing efficient cryptographic primitives by using multilinear mapping structures. However, not until 2013 Garg, Gentry and Halevi (GGH)[9] proposed the candidate multilinear mapping structure based on the ideal lattice. Based on GGH's program, many public key encryption schemes are designed, such as in Refs. [10-11]. Following the idea of GGH, several multilinear mapping schemes are proposed. Langlois et al.[12] proposed a GGH variant scheme. Jean-Sébastien Coron, Tancrède Lepoint, and Mehdi Tibouchi (CLT)[13] designed a multilinear mapping structure based on integer instead of ideal lattice. Although the CLT scheme is cracked by Cheon et al.[14] by zero attack, CLT proposed a modified multilinear mapping structure based on integer which can avoid zero attack[15]. Recently, Hu et al.[16] can attack GGH effectively with zero attack. While Gu[17] proposed new multilinear mapping structure without zero encodings, thus completely eradicating the zero attack.
At present, the known multilinear mapping encoding systems all adopt the GGH's idea of "graded". And they have similar algorithms like sample level-0 encoding, level-i encoding, extraction and 0 encoding decision. According to these features, we propose a generic graded multilinear mapping encoding system, disregarding the data structure and concrete realization of an encoding system. As with the definition of GDDH, we define the generic graded decision Diffie-Hellman problem (GGDDH).
In the application of public key encryption, once the user secret key is leaked, the past cipher can be easily decrypted by intruder. Some people proposed some solutions such as in Ref. [18]. In 1997, Anderson[19] firstly introduced the idea of forward-security in the key exchange protocol to public key cryptosystem, in order to solve the leakage problem of private key. Inspired by his idea, a series of forward-secure public key cryptosystems are proposed. Li et al.[20] designed forward secrecy signcryption scheme based on elliptic curve cryptosystem. The landmark is that in 2003, Canetti et al.[21] firstly constructed a forward-secure public key encryption scheme, based on a hierarchical encryption scheme[22]. Subsequently, Canetti et al.[23] also gave a general method of constructing the forward-secure public key encryption scheme using binary tree. This method has been widely applied to the design of forward-secure encryption scheme based on identity[24-25] and forward-secure encryption scheme based on the certificate[26]. David and Olivier[27] proposed a forward-secure non interactive key exchange protocol that also used the binary tree[23] to design.
Based on the generic graded multilinear mapping encoding system, we design a forward-secure multi-receiver signcryption scheme. Our scheme also uses binary tree to manage the evolution of the user's private key. The entire life cycle of the user private key is divided into N time period, and each time period is only corresponding to a node of binary tree. Beginning from the first time period, the user's private key evolves each time after a time period finishes, and user destroys the private key of the current time period. But the public key is kept unchanged. The sender uses the current time period and the private key to signcrypt message and only the recipient with the private key in the same time period can decrypt and verify successfully.
This ensures that in current time period if the private key of the recipient is exposed, the ciphertext created in the past time period is still safe. This also ensures when the current time period private key of the sender is exposed, the attacker still cannot forge the signcryption of the past time period.
Our contributions: firstly, we define the generic graded multilinear mapping encoding system and assumption of the generics graded decision Diffie-Hellman problem (GGDDH). Moreover, we design a forward-secure multi-receiver signcrypiton scheme based on the generic graded multilinear mapping encoding system, and prove it security under the assumption of GGDDH problem.
Secondly, for the first time we elaborate the forward-secure multi-receiver signcryption security model. Basically, a multi-receiver signcryption scheme should guarantee the message confidentiality and unforgeability at any time period. At the same time, in order to guarantee the forward security, if the private key is leaked in time period j, and then the message confidentiality should be guaranteed in i < j; similarly, if the private key of the sender is leaked in j, the scheme can guarantee that attacker cannot forge signcryption in i < j.
Thirdly, there are two group elements in the ciphertext of our scheme much less than the number of group elements in Refs.[3-4]. Because in Refs.[3-4], the length of the ciphertext and the number of the receivers are linear, the size of ciphertext is expanding quickly with the number of receivers increasing. Meanwhile, the existing multi-receiver schemes are designed mainly based on bilinear and the bilinear problem has polynomial time quantum solution. However, there is no polynomial time quantum solution of GGDDH problem on which our scheme is proposed based.
2 Preliminaries 2.1 Generic Graded Multilinear Mapping Encoding SystemDefinition 1 Generic Graded Multilinear Mapping Encoding System. For the cyclic group G1, GT with the same order p, a level-κ multilinear mapping e:G1×…×G1→GT is satisfied e(α1g, α2g, …, ακg)=
1) The system initial algorithm InstGen(1λ, 1κ) takes as input security parameter λ and maximum encoding level κ. It returns public parameters params.
2) The level-0 encoding sampling algorithm samp() takes as input public parameters params. It returns a random level-0 encoding d.
3) The level-i encoding algorithm enc(i, d) takes as input public parameters params, i≤κ and level-j encoding d, such that j≤i. It returns level-i encoding of d. The process of encoding includes the default randomization process, that is, the noise is added to the encoding.
4) The add algorithm add (u1, u2) takes as input level-i encoding u1, u2. It returns the sum of u1 and u2, that is level-i≤κ encoding u=u1+u2.
5) The multiply algorithm mult(u1, u2) takes as input level-i encoding u1 and level-j encoding u2, such that i+j≤κ.It returns level-(i+j) encoding u=u1·u2.
6) The zero test algorithm is Zero(u) takes as input encoding u. It returns 1 if u is zero encoding, otherwise it returns 0.
7) The extraction algorithm ext(u) takes as input level-κ encoding u. It returns according characteristic bit string b∈{0, 1}λ.
For convenience's sake, and under circumstances of no confusion, we will directly use the mathematical symbols '+' and '·' instead of add(u1, u2) and mult(u1, u2).
Similar to the definition of GDDH problem, we give the definition of generic graded decision Diffie-Hellman problem (GGDDH).
Definition 2 GGDDH problem. Considering the process described below, and the attacker is given the parameters params.
1) ej←samp(), j=0, 1, …, κ; //randomly sample κ+1 level-0 encodings
2) Let uj←enc(1, ej), j=0, 1, …, κ;
3) f←samp(); //randomly sample a level-0 encoding
4) Let
The generic graded decision Diffie-Hellman problem (GGDDH) is how to distinguish v and v′ for an attacker. In other words, how to distinguish the distribution DGGDDH={params, u0, …, uk, v} and distribution DRAND={params, u0, …, uk, v′} for an attacker.
2.2 Definition of Forward-Secure Multi-Receiver Signcryption SchemeThis section defines the notion of forward-secure multi-receiver signcryption scheme (fs-MSC). A formal definition follows:
Definition 3 A (public key) forward-secure multi-receiver signcryption scheme(fs-MSC) is a tuple of PPT (probabilistic polynomial time) algorithms (KeyGen, Upd, fs-Signcrypt, fs-DeSigncrypt) such that:
1) The key generation algorithm KeyGen takes as input a security parameter λ and the total number of time periods N. It returns a public key pksand an initial secret key sks for sender IDs and pair of public key and private key for every receiver in {ID1, ..., IDτ} in addition to some public parameters denoted as PP.
2) The key update algorithm Upd takes as input PP, current time period i∈[0, N-1), and the associated secret key ski. It returns the secret key ski+1 for the next time period i+1.
3) The encryption algorithm fs-Signcrypt takes as input the name of a node s∈Sn which represents the current time period, the receiver set ID1, …, IDτ, sender IDs's private key sks and message M. It returns a signcryption C.
4) The decryption algorithm fs-DeSigncrypt takes as input a receiver IDi's private key ski, a ciphertext C, the current time period i. It returns correct plaintext M∈{0, 1}
In this section we presents an fs-MSC scheme based on the generic graded multilinear mapping. As described in the introduction, our scheme uses binary tree to manage the evolution of the user's private key. The entire life cycle of the user private key is divided into N time period, and each time period only corresponds to one node of binary tree. The order of time period is the same as the pre-order traversal of the binary tree.
As shown in Fig. 1, each node of the binary tree corresponds to a random selection of level-0 encoding hs, where s is the path from the root node to this node (not including the root node). Time period i is often represented by s of the tree node. The level-1 encoding of the level-0 encoding x of the root node is the public key. The level-1 encoding of the other nodes Hs=enc(1, hs) are public parameters and hs will be destroyed. From the property of the binary tree, after getting rid of the root node, if level of binary tree is n, and then the set of all path is sn, such that |sn|=2n+1-2, so, the total time period is N=2n+1-2.
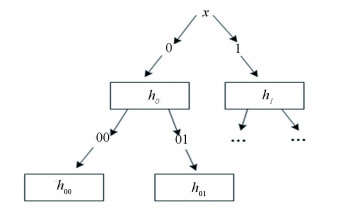
|
Figure 1 Private key evolution binary tree |
If a path of binary tree node is s=b1b2…b
Supposed the path length of a binary-tree node is
Supposed that total time period is N=2n+1-2, where n is the level of binary tree(get rid of root node), and the maximum multilinear encoding level κ=n+2. Our fs-MSC scheme has the following algorithms.
1) KeyGen(1κ, 1λ): first of all, generate multilinear mapping parameters params. Then randomly sample n-1 level-0 encodings (g2, g3, …, gn)←samp(), and make their level-1 encoding (G2, G3, …, Gn) public. Sample level-0 encoding hs←samp() for bit string s∈Sn corresponding to every binary tree node. Make Hs=enc(1, hs) public and destroy hs. Lastly, output PP={params, (G2, G3, …, Gn), {Hs}}.
Pick a random level-0 encoding xs for sender IDs and compute private key sks=0=(z0, z1)=(enc(1, x·H0), enc(1, x·H1)), public key pks=enc(1, xs). Choosing two random level-0 encodings xi, 1, xi, 2 for each receiver IDi∈{ID1, …, IDτ}. Let xi=xi, 1·xi, 2, to compute receiver's private key sks, i=(z0, i, z1, i)=(enc(1, xi·H0), enc(1, xi·H1)). To compute receiver's public key (pki, 1, pki, 2)=(enc(1, xi, 1), enc(1, xi, 2)).
2) Upd(sks): Supposed that s=b1b2…b
(1) If the length of path
(2) If
3) fs_Signcrypt(PP, M, s, ∪1≤i≤τ(IDi), sks):Taking as input the sender IDs's private key sks, receiver set ∪1≤i≤τ(IDi) with public key ∪1≤i≤τ(pki, 1, pki, 2). IDs chooses level-0 encoding r←samp() at random, and computes c1←enc(1, r).Then to compute c2, i←ext(r·zs·
4) fs_DeSigncrypt(PP, c, s, sks, i): Taking as input the cipher and private key of number i receiver sks, i. The decryption algorithm outputs M←ext(c1·zs, i·pks·
Correctness: r·zs·
Performance Comparison and efficiency Analysis: There is simply Ο(n) multiply on polynomial ring in the encryption algorithm, the same as the decryption algorithm. Since our scheme does not need paring computation and exponentiation, so our scheme has lower computational complexity compared to the existing multi-receiver encryption scheme as shown in Table 1.
| Table 1 Performance comparison between our scheme and other multi-receiver signcryption |
There are Ο(n) group elements in the ciphertext of Refs. [3-4], and only Ο(1) group elements in our scheme. Thus, the length of ciphertext of our scheme is significantly reduced.
Finally, with regard to the safety of contrast, the last column of Table 1 (Quantum Algorithm) means whether there is a polynomial time quantum algorithm to solve the hardness assumption like BDH and GGDDH. It is seen from the foregoing, BDH problem has polynomial time quantum algorithm, so the schemes [3, 4, 24] will be unsafe in the post quantum era. In addition, the scheme [3-4] does not meet the demand of forward secure. If the user secret key is leaked, the past cipher can be easily decrypted.
In Table 1, 丨G1丨is the bit length of one element in group G1; 丨ID丨is the bit length of one receiver identity ID and丨m丨means the bit length of plaintext m. Meanwhile, n is the number of receiver and N is the total number of time period.
4 Security of Our Construction 4.1 Security ModelA secure fs-MSC scheme should keep the secrecy of signcryption in a time period s even if the private key of other nodes (as long as they are not the ancestors of s) has been exposed. As mentioned in Ref. [23], we define the attack scenario a selective-node (SN) attack, in which the adversary is required to provide the target node in advance(i.e., before seeing the public key). First of all, we give the definition of message confidentiality and unforgeability.
Definition 4 A fs-MSC scheme is confidentiality secure against selective-node, and chosen-plaintext attacks (secure in the sense of SN-CPA) if for all PPT adversaries Α, the advantage of A in the following game is negligible in the security parameter λ.
Init: Α outputs a name s*∈Sn of a node which represents a specified time period. Simulator calls KeyGen(1κ, 1λ) outputs public parameters PP. Without loss of generality, we specify the sender IDs* with the public key pks*and the set of receiver's identity R*={ID1*, …, IDτ*} with public key {(pki, 1, pki, 2)}. Simulator calls Keygen(1κ, 1λ) to get sender's private key SKs* and private key of each receiver.
Queries: Α can make two types of query to simulator Β.
-Create new key: Α is given pks*, {(pki, 1, pki, 2)}and {sks} that is the set of private key of sender and receivers for any node in Sn as long as s is not a prefix of s*.
-Signcrypt: On input a message M∈{0, 1}ℯ. Then simulator calculates c←fs_Signcrypt(PP, M, s*, R*, sks*) and returns c to A.
Challenge: Α generates a request challenge (s*, M0, M1). Simulator Β selects a random bit β∈{0, 1} and computes c←fs_Signcrypt(PP, Mβ, s*, R*, sks*). Finally, the adversary is given c.
Guess: The adversary outputs a guess β′∈{0, 1}. It succeeds if β′=β. The adversary's advantage is the absolute value of the difference between its success probability and 1/2.
Definition 5 A fs-MSC scheme is unforgeability secure against selective-node, and chosen-plaintext attacks (secure in the sense of SN-CPA) if for all PPT forger F, the advantage of F in the following game is negligible in the security parameter λ.
The init and queries are defined as in Definition 4.
Forge: Finally, F outputs new legal signcryption for a message M that can be decrypted by any receiver in R*={ID1*, …, IDτ*} and the sender IDs* can be verified. The advantage of F is the probability of his success.
On the basis of message confidentiality and unforgeability, our scheme also ensures the forward-security. The definition of message forward-confidentiality and forward-unforgeability is as follows.
Definition 6 A fs-MSC scheme is forward-confidentiality against chosen-plaintext attacks (secure in the sense of fs-CPA) if for all PPT adversaries whose advantage in the following game is negligible in the security parameter λ.
Setup: Simulator calls KeyGen(1κ, 1λ) outputs public parameters PP. Without loss of generality, we specify the sender IDs* with the public key pks* and private key sks* and receiver IDi in R*={ID1*, …, IDτ*} has public key {(pki, 1, pki, 2)}.
Queries: The adversary is allowed one breakin (i) query and one challenge (j, M0, M1), in either order, such that 0≤j < i < N. On breakin (i) query, the sender's private key ski in i time period is given to the adversary.
Challenge: The adversary generates a request challenge(j, M0, M1). Simulator Β selects a random bit β∈0, 1 and computes c←fs_Signcrypt(PP, Mβ, j, R*, sks*). Finally, the adversary is given c.
Guess: The adversary outputs a guess β′∈0, 1. It succeeds if β′=β. The adversary's advantage is the absolute value of the difference between its success probability and 1/2.
Definition 7 A fs-MSC scheme is forward-unforgeability against selective-node, and chosen-plaintext attacks (secure in the sense of SN-CPA) if for all PPT forger F, the advantage of F in the following game is negligible in the security parameter λ.
The setup and queries are defined as in Definition 6.
Forge: Finally, F outputs new legal signcryption for a message M in j time period that can be decrypted by any receiver in R*={ID1*, …, IDτ*} and the sender IDs* can be verified. The advantage of F is the probability of his success.
4.2 Proof of Confidentiality for fs-MSC SchemeWe show that if there exists a PPT attacker Α that can win the game defined in Definition 4 with non-negligible advantage ε for our fs-MSC scheme, and then there exists a PPT simulator Β that can break the GGDDH problem with the same advantage.
Theorem 1 For our fs-MSC scheme, if there is any probability polynomial time (PPT) attacker A that can win the game defined in Definition 4 with non-negligible advantage ε, and then there is an algorithm Β for solving generic graded DDH(GGDDH) problem with the same advantage.
Proof:The simulator takes as input the GGDDH instance (params, u0, …, uκ, v) and acts as the role of challenger.The parameter params is public.
Init: Α outputs a specified time period named s*∈Sn. Supposed that the time period |s*|=ℯ and s*=b1b2…bℯ, let Hb1b2…bi=ui, i=1, 2, …, ℯ. Let Gi=ui, i=ℯ+1, …, n. Choosing hs←samp() at random and compute Hs=enc(1, hs) such that s∈Sn and s is not a prefix of s*. Simulator samples level-0 encoding xs for sender IDs*, to compute his private key sks=0=(z0, z1)in the first time period and public key pks*=enc(1, xs). Simulator chooses level-0 encoding xi for each receiver in R*={ID1*, …, IDτ*}\{ID1*}, and computes the public key/private key pair ((pki, 1, pki, 2), (sks, i)). Without loss of generality, let public key of receiver ID1* be (pki, 1, pki, 2)=(un+1, un+2). At last, forger Α is given pks*, {(pki, 1, pki, 2)}.
At last, invader is given public parameters and the public key of sender and every receiver.
Queries:Α can make two types of query to the simulator Β.
-Create new key: Α can query {sks}that is the set of private key of any reciever for any node in Sn as long as s is not a prefix of s*.
-Signcrypt: On input a message M∈{0, 1}ℯ. Then simulator calculates c←fs_Signcrypt(PP, M, s*, R*, sks*) and returns c to Α.
Challenge:Α inputs a pair of message(M0, M1). Β chooses β∈0, 1 randomly. The simulator lets c1←u0 and computes c2, 1←ext(xs·v)ⓧMβ, c2, i←ext(c1·zs·
Guess: Α outputs his guess β′∈0, 1 for β. If β′=β, Β judges v=e0
The parameters that Β releases are independently distributed random variables, and consistent with the real scheme. Obviously, if v=
We show that if there exists a PPT forger F that can win the game defined in Definition 5 with non-negligible advantage ε for our fs-MSC scheme, and then there exists a PPT simulator Β that can break the GGDDH problem with the same advantage ε.
Theorem 2 For our fs-MSC scheme, if there exists any probability polynomial time(PPT) forger F that can win the game defined in Definition 5 with non-negligible advantage ε, then there exists an algorithm Β for solving generic graded DDH(GGDDH) problem with the same advantage.
Proof:The simulator takes as input the GGDDH instance (params, u0, …, uk, v) and acts as the role of challenger.
Init:F outputs a name s*∈Sn of a node which represents a specified time period. Supposed the time period s*=b1b2…b
Query phases:F can make two kinds of query to Β.
-Create new key: F can query {sks}that is the set of private key for any node in Sn as long as s is not a prefix of s*.
-Signcrypt: On input a message M∈{0, 1}
Response:At last, F outputs a signcryption c*=(c1, c2, c3). If signcryption is legal, Β judges v=
Obviously, if v=
We show that if there exists a PPT attacker Α that can win the game defined in Definition 6 with non-negligible advantage ε for our fs-MSC scheme, and then there exists a PPT simulator Β that can break the GGDDH problem with non-negligible advantage.
Theorem 3 For our fs-MSC scheme, if there is any probability polynomial time (PPT) attacker A that can win the game defined in Definition 6 with non-negligible advantage ε, and then there is an algorithm Β for solving generic graded DDH(GGDDH) problem with non-negligible advantage.
Proof:The simulator takes as input the GGDDH instance (params, u0, …, uκ, v) and acts as the role of challenger.The parameter params is public.
Init:Simulator calls KeyGen(1κ, 1λ) outputs public parameters PP. Α outputs challenge (j, M0, M1). The name s*∈Sn of a node correspond to the time period j. Supposed the time period s*=b1b2…b
Queries:The adversary is allowed one breakin (i) query, such that 0≤j < i < N. On query breakin(i), each receiver's private key in i time period that is computed via repeated calling of Upd in the normal way is given to the adversary.
Challenge:Simulator Β chooses β∈0, 1 randomly. The simulator let c1←u0. Then, computes c2, 1←ext(xs·v)ⓧMβ, c2, i←ext(c1·zs·
Guess:Α outputs his guess β′∈0, 1 for β. If β′=β, Β judges v=
If the attacker obtains the private key in the time period i, the private key of the future time period can be calculated, so we allow the attacker to query once.
In the process of challenge, if v=
We show that if there exists a PPT attacker F that can win the game defined in Definition 7 with non-negligible advantage ε for our fs-MSC scheme, and then there exists a PPT simulator Β that can break the GGDDH problem with non-negligible advantage.
Theorem 4 For our fs-MSC scheme, if there is any probability polynomial time (PPT) attacker A that can win the game defined in Definition 7 with non-negligible advantage ε, there is an algorithm Β for solving generic graded DDH(GGDDH) problem with non-negligible advantage.
Proof:We show that if there exists a PPT attacker F that can win the game defined in Definition 5 with non-negligible advantage ε for our fs-MSC scheme, there exists a PPT simulator Β that can break the GGDDH problem with non-negligible advantage. The simulator takes as input the GGDDH instance (params, u0, …, uκ, v) and acts as the role of challenger.The parameter params is public.
Init: The simulator calls KeyGen(1κ, 1λ) and outputs public parameters PP. F outputs a name s*∈Sn of a node which represents a specified time period j. Supposed the time period s*=b1b2…bℯ, let Hb1b2…bi=ui, i=1, 2, …, ℯ. Choose hs←samp() at random and compute Hs=enc(1, hs) such that s∈Sn and s is not a prefix of s*.Let Gi=ui, i=ℯ+1, …, n. Simulator lets sender IDs*'s public key pks*=u0. Simulator chooses level-0 encoding xi for each receiver in R*={ID1*, …, IDτ*}\{ID1*}, and computes the public key/private key pair ((pki, 1, pki, 2), (sks, i)). Without loss of generality, let public key of receiver ID1* be (pki, 1, pki, 2)=(un+1, un+2).At last, forger F is given pks*, {(pki, 1, pki, 2)}.
Queries:The adversary is allowed one breakin (i) query, such that 0≤j < i < N. On query breakin (i), sender's private key in i time period can be calculated and given to the adversary because the simulator keep {hs}, such that s∈Sn and s is not a prefix of s*.
Response: At last, if F outputs a legal signcryption c*=(c1, c2, c3) of message M from IDs* to R*. Because c3←enc(ℯ, M·hash(
In this paper, a generic multilinear mapping encoding system is defined, based on which a forward-secure multi-receiver signcryption scheme is designed. The security scheme of a forward-secure multi-receiver signcryption scheme is proposed, which can effectively repair the loss in a public key system because the leakage of current private key.
| [1] |
Zheng Yuliang.
Digital signcryption or how to achieve cost(signature & encryption) < < cost(signature)+ cost(encryption). Heidelberg: Springer-Verlag, 1997 : 165 -179.
( 0) 0)
|
| [2] |
Baek J, Safavi-Naini R, Susilo W.
Efficient multi-receiver identity based encryption and its application to broadcast encryption. Proceedings of the 8th Int Workshop on Theory and Practice in Public Key Cryptography. Heidelberg: Springer-Verlag, 2005 : 380 -397.
( 0) 0)
|
| [3] |
Elkamchouchi H, Abouelseoud Y.
An efficient provably secure multi-recipient identity-based signcryption scheme. Proceedings of IEEE ICNM'09. Piscataway: IEEE, 2009 : 70 -75.
( 0) 0)
|
| [4] |
Lal S, Kushwah P. Anonymous ID based signcryption scheme for multiple receivers. http://eprint.iacr.org/2009/345.pdf, 2009-07-12.
( 0) 0)
|
| [5] |
Shi W, Kumar N, Gong P, et al. On the security of a certificateless online/offline signcryption for internet of things.
Peer-to-Peer Networking and Applications, 2015 , 8 (5) : 881-885.
DOI:10.1007/s12083-014-0249-3 ( 0) 0)
|
| [6] |
Pang L, Gao L, Li H, et al. Anonymous multi-receiver ID-based signcryption scheme.
IET Information Security, 2015 , 9 (3) : 194-201.
DOI:10.1049/iet-ifs.2014.0360 ( 0) 0)
|
| [7] |
Shor P W. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer.
SIAM J Comput, 1997 , 26 (5) : 1484-1509.
DOI:10.1137/S0097539795293172 ( 0) 0)
|
| [8] |
Dan Boneh, Alice Silverberg. Applications of multilinear forms to cryptography.
Contemporary Mathematics, 2003 , 324 : 71-90.
DOI:10.1090/conm/324 ( 0) 0)
|
| [9] |
Sanjam Garg, Craig Gentry, Shai Halevi.
Candidate multilinear maps from ideal lattices. Proceedings of EUROCRYPT 2013. Heidelberg: Springer-Verlag, 2013 : 1 -17.
( 0) 0)
|
| [10] |
Jing Zhengjun, Jiang Guoping, Gu Chunsheng.
A verifiable multi-recipient encryption scheme from multilinear maps.Proceedings of 2014 Ninth International Conference on P2P, Parallel, Grid, Cloud and Internet Computing (3PGCIC). Piscataway: IEEE , 2014 : 151 -156.
( 0) 0)
|
| [11] |
Hohenberger S, Sahai A, Waters B. Full domain hash from (leveled) multilinear maps and identity-based aggregate signatures. http://eprint.iacr.org/2013/434.pdf, 2013-07-09.
( 0) 0)
|
| [12] |
Langlois A, Stehlé D, Steinfeld R.
GGHLite: More efficient multilinear maps from ideal lattices. Proceedings of EUROCRYPT 2014. Heidelberg: Springer-Verlag, 2014 : 239 -256.
( 0) 0)
|
| [13] |
Coron J-S, Lepoint T, Tibouchi M.
Practical multilinear maps over the integers. Proceedings of Crypto 2013. Heidelberg: Springer-Verlag, 2013 : 476 -493.
( 0) 0)
|
| [14] |
Cheon J H, Han K, Lee C, et al. Cryptanalysis of the multilinear mapping over the integers. http://eprint.iacr.org/2014/906.pdf, 2014-11-03.
( 0) 0)
|
| [15] |
Coron J-S, Lepoint T, Tibouchi M. New multilinear maps over the integers. http://eprint.iacr.org/2015/162.pdf, 2015-02-25.
( 0) 0)
|
| [16] |
Hu Yupu, Jia Huiwen. Cryptanalysis of GGH Map. http://eprint.iacr.org/2015/301.pdf, 2015-04-07.
( 0) 0)
|
| [17] |
Gu Chunsheng. Multilinear maps using random matrix. http://eprint.iacr.org/2015/463.pdf, 2015-05-19.
( 0) 0)
|
| [18] |
He Jingsha, Liu Gongzheng, Zhao Bin, et al. Ensuring the authenticity and non-misuse of data evidence in digital forensics.
Journal of Harbin Institute of Technology(New Series), 2015 , 22 (1) : 85-90.
DOI:10.11916/j.issn.1005-9113.2015.01.014 ( 0) 0)
|
| [19] |
Anderson R. Two remarks on public key cryptology. Invited Lecture at the 4th ACM Conference on Computer and Communications Security, Cambridge:University of Cambridge, 1997.
( 0) 0)
|
| [20] |
Li Fangwei, Wang Jian, Chen Guanghui. Forward secrecy sign-cryption scheme based on elliptic curve cryptosystem.
Journal of Beijing University of Posts and Telecommunications, 2006 , 29 (1) : 22-25.
( 0) 0)
|
| [21] |
Canetti R, Halevi S, Katz J.
A forward-secure public key encryption scheme. Proceedings of the Eurocrypt 2003. Heidelberg: Springer-Verlag, 2003 : 255 -271.
( 0) 0)
|
| [22] |
Gentry C, Silverberg A.
Hierarchical ID-based cryptography. Proceedings of the Asiacrypt 2002. Heidelberg: Springer-Verlag, 2002 : 548 -566.
( 0) 0)
|
| [23] |
Canettir R, Halevi S, Katz J. A forward-secure public-key encryption scheme.
Journal of Cryptology, 2007 , 20 : 265-294.
DOI:10.1007/s00145-006-0442-5 ( 0) 0)
|
| [24] |
Yao D, Fazio N, Dodis Y, et al. ID-based encryption for complex hierarchies with applications to forward security and broadcast encryption. Proceedings of the 11th ACM CCS.
New York, 2004 : 354-363.
( 0) 0)
|
| [25] |
Yu J, Kong F Y, Cheng X G, et al. forward-secure identity-based public-key encryption without random oracles.
Fundamenta Informaticae, 2011 , 111 (2) : 241-256.
( 0) 0)
|
| [26] |
LU Y, LI J G. Forward-secure certificate-based encryption and its generic construction.
Journal of Networks, 2010 , 5 (5) : 527-534.
( 0) 0)
|
| [27] |
David Pointcheval, Olivier Sanders. Forward Secure Non-Interactive Key Exchange. Proceedings of SCN 2014. Amalfi, 2014. 21-39.
( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


