2. Shanghai Construction Group Co. Ltd., Shanghai 200080, China
Researchers pay much attention to the influence of microscopic mechanical characters in macroscopic material because it is an effective way to explore the properties of porous material for engineering problems. Early time, Rice and Tracy[1]tried to describe the fracture process of rigid plastic porous material containing periodic circular voids. Then, Gurson[2] proposed a constitutive model called ‘Curson' from the view of phenomenology which was used to reflect the effect of the growth of voids in micro-level on the behavior of macro-level. This study helped a lot on the numerical simulation to tensile failure[3]. Taking the porous medium shaped by periodic circular voids as the object, Guennouni and Francois[4] started the research on macroscopic constitutive equations for viso-plastic porous material and then compared their results with the conclusions of Rice and Tracy as well as those of Gurson. Garajeu and Suquet[5] derived the material dissipated energy of a rigid perfectly plastic solid element on the basis of generalized “Curson” model, whose research object turned into the porous medium comprised of particles.
In recent years, the research about constitutive laws for plastic or visco-plastic porous materials keeps going mainly depending on numerical approaches. Danas et al.[6] put forward a second-order nonlinear homogenous constitutive equation used to evaluate the mechanical behavior of isotropic visco-plastic porous material. Fritzen et al.[7] made a research on porous metal materials containing circular voids whose distribution obeyed Monte Carlo type.
Among these researches, the pore shape and interaction between main voids and secondary cavities are always the focuses. About pore shape, Flandi and Leblond[9] proposed an improved non-linear viscous constitutive law for considering pore shape. Then, Julien[10] got a semi-analytical model for saturated porous material and the model took the different sizes of circular voids into consideration. Danas and Aravas[10] proposed a modified numerical constitutive law related to the pore shape for elastic-plastic porous materials on the basis of the research of Kailasam and Castaneda[11-12]. About the interaction between main voids and secondary cavities, Guennouni and Francois[13] firstly took the main void and secondary cavities into account and summarized the impact on macroscopic behaviors of the plastic material with a circular hole in center. Successively, Li et al.[14] studied the ductile fracture caused by the secondary cavities. According to “Gurson” model, Fabregue and Pardoen[15] explored the stress potential of elastic-plastic alloy materials containing main and secondary voids.
In previous studies, most constitutive models were created based on one kind of void, the circular one. Though researchers took cares of the impact of pore shape on macroscopic mechanical behaviors, they did not give explicit equation containing the parameter of pore shape. Guennouni and Francois just analyzed the difference of yield functions when the pore was circular and elliptic. Research on two-scale voids is inadequate and most of the voids keep circular.
In the present work, the macroscopic constitutive laws for visco-plastic porous medium shaped by regularly distributed circular particles are derived and improved on the basis of the achievement got by Guennouni and Francois[4, 13]. The pore shape determined by the axial ratio of particles and interaction between the main void and secondary cavities are considered during approximating the macroscopic yield criterion for rigid plastic material and the macroscopic potential for Norton-Hoff material. In many engineering problems, we just focus on medium's macroscopic properties and states, such as compaction to porous asphalt concrete. So the macroscopic constitutive law can be conveniently applied to such simulation by viewing porous medium as homogeneous.
2 Constitutive Laws for a Norton-Hoff and Rigid Plastic Materials 2.1 Micro-constitutive LawsThe micro-constitutive law for a Norton-Hoff material is defined as[4]:
| ${{\dot{\varepsilon }}_{ij}}\left( \upsilon \right)=\frac{\partial {{\varphi }_{q}}\left( \sigma \right)}{\partial {{\sigma }_{ij}}}$ | (1) |
with ${{\dot{\varepsilon }}_{ij}}\left( v \right)=\frac{\partial {{\varphi }_{q}}\left( \sigma \right)}{\partial {{\sigma }_{ij}}}$.
${{\dot{\varepsilon }}_{ij}}\left( v \right)$ is the strain rate tensor and ν is the velocity field. φq(σ) stands for the stress dissipative potential for a Norton-Hoff material.
| ${{\varphi }_{q}}\left( \sigma \right)=\frac{{{{\dot{\varepsilon }}}_{0}}{{\sigma }_{0}}}{q}\left( \frac{{{\sigma }_{e}}}{{{\sigma }_{0}}} \right)q$ | (2) |
with σe=[(3/2)sijsij]1/2.
${{\dot{\varepsilon }}_{0}}$, σ0 and σe are the yield strain rate, yield stress and equivalent stress for Von Mises yield criterion respectively. p and q mean the hardening exponents for Norton-Hoff law with relation of q+p=pq.
In the case of a rigid plastic material, Eq.(1) turns into[4]:
| ${{{\dot{\varepsilon }}}_{ij}}\left( \upsilon \right)=\lambda \frac{\partial {{\varphi }_{\infty }}\left( \sigma \right)}{\partial {{\varphi }_{ij}}}$ | (3) |
where φ∞(σ)stands for the Von Mises yield function that can be defined as Eq.(4) . λ is a positive real that found in the real way. A rigid perfectly plastic material can be approximated by a series of Norton-Hoff materials whose hardening exponent q reaches infinity. That is, the viscosity is not considered.
| ${{\varphi }_{\infty }}\left( \sigma \right)=\frac{{{\sigma }_{e}}}{{{\sigma }_{0}}}\le 1$ | (4) |
Substituting Eq.(4) into Eq.(2) , we can get the relation between the Norton-Hoff potential and Von Mises yield function:
| ${{\varphi }_{q}}\left( \sigma \right)=\frac{{{{\dot{\varepsilon }}}_{0}}{{\sigma }_{0}}}{q}\left( {{\varphi }_{\infty }}\left( \sigma \right) \right)q$ | (5) |
Based on micro-constitutive laws, the macro-constitutive law of porous media is proposed by homogenization technique in the part. A Representative Element Volume (REV), S, consisting of quarter particles is involved (Fig. 1) . Adjacent particles fuse with each other, which means that there is no interaction between them during compaction. The REV's force boundary condition is defined as macroscopic stress Σ. Microscopic velocity and stress field obey the usual equilibrium equations with the following boundary conditions:
| $\sigma \centerdot n=\sum{\centerdot }nalong{{\Gamma }_{e}}$ | (6) |
| $\sigma \centerdot n=0along{{\Gamma }_{i}}$ | (7) |
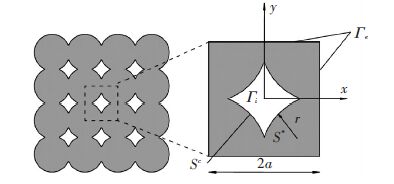
|
Figure 1 Elementary cell containing a void (REV) |
The macroscopic strain rate is defined as:
| ${{{\dot{E}}}_{ij}}=\frac{1}{2S}{{\int }_{{{\Gamma }_{e}}}}\left( {{\upsilon }_{i}}{{n}_{j}}+{{\upsilon }_{i}}{{n}_{j}} \right)d\Gamma $ | (8) |
which can be also expressed:
| ${{{\dot{E}}}_{ij}}=\frac{1}{S}\left( {{\int }_{S*}}{{{\dot{\varepsilon }}}_{ij}}\left( \upsilon \right)ds+\frac{1}{2}{{\int }_{{{\Gamma }_{i}}}}\left( {{\upsilon }_{i}}{{n}_{j}}+{{\upsilon }_{i}}{{n}_{j}} \right)d\Gamma \right)$ | (9) |
where S=S*+Sc, Sc stands for the void.
In macroscopic level, the porous medium is viewed as homogeneous without voids. The macro-constitutive law for it is a function of macroscopic stress Σ and strain rate $\dot{E}$. In the case of Norton-Hoff material, taking Eq.(1) as reference and combining the homogenization technique, its macro-constitutive equation can be expressed as:
| ${{{\dot{E}}}_{ij}}=\frac{\partial {{\Phi }_{q}}\left( \sum \right)}{\partial {{\sum }_{ij}}}$ | (10) |
with Φq(Σ)=$\frac{1}{S}$∫S*φq(σ)ds. Φq is the macroscopic stress potential for homogeneous equivalent Norton-Hoff material.
In the case of rigid plastic material, it is infeasible to express $\dot{E}$ by the means of Eq.(8) because its microscopic velocity field is not unique and regular any more. So we have to directly compute the macroscopic yield function Φ∞ by building the domain K that just contains admissible macroscopic stress[4]. The macroscopic yield criterion for rigid plastic material also satisfies:
| ${{\Phi }_{\infty }}\left( \sum \right)\le 1$ | (11) |
For convenience, the macroscopicstress state Σ and strain rate state $\dot{E}$ of the REV are expressed by Σ′m, Σ′eq and $\dot{E}$′m, $\dot{E}$′eq respectively. The calculating formulae are shown as follows:
| ${{{{\sum }'}}_{m}}=0.5\left( {{{{\sum }'}}_{xx}}+{{{{\sum }'}}_{yy}} \right)$ | (12a) |
| ${{{{\sum }'}}_{eq}}={{\left[ \left( {3}/{2}\; \right){{S}_{ij}}{{S}_{ij}} \right]}^{{1}/{2}\;}}/k$ | (12b) |
where Σ′=Σ/k, k is the Von Mises shear stress. Sij is the macroscopic deviatoric part of stress tensor.
| ${{{{\dot{E}}'}}_{m}}=\frac{\sqrt{3}{{{\dot{E}}}_{m}}}{2{{{\dot{\varepsilon }}}_{0}}}$ | (13a) |
| ${{{{\dot{E}}'}}_{eq}}={{\left\{ \frac{2}{3}\left( {{{{\dot{E}}'}}_{ij}}-\frac{1}{3}{{{{\dot{E}}'}}_{m}}{{\delta }_{ij}} \right)\left( {{{{\dot{E}}'}}_{ij}}-\frac{1}{3}{{{{\dot{E}}'}}_{m}}{{\delta }_{ij}} \right) \right\}}^{{1}/{2}\;}}$ | (13b) |
where $\dot{E}$m=$\frac{1}{2}$($\dot{E}$xx+$\dot{E}$yy), $\dot{E}$′ij=$\frac{{{{\dot{E}}}_{ij}}}{\sqrt{3}{{{\dot{\varepsilon }}}_{0}}}$. For the plain strain problem, $\dot{E}$zz=$\dot{E}$zx=$\dot{E}$zy=0.
3 Numerical Research for Macroscopic Constitutive LawsAll the numerical calculations are implemented by the finite element analysis software MSC.MARC. The material type is defined as rigid-plastic which obeys Von Mises yield criterion. By means of the subroutine interface offered by the software itself, the yield stress can be varied randomly for meeting the numerical models' demands. The NO.155 element characterized with four-point triangular and isoparametric is chosen. This kind of element is usually used to analyze the incompressible material.
One point needs to be emphasized here. In the macroscopic level, the material is considered homogenous from the view of yield function and stress potential. So the following numerical calculations and analysis do not take the stress concentration in REV into account.
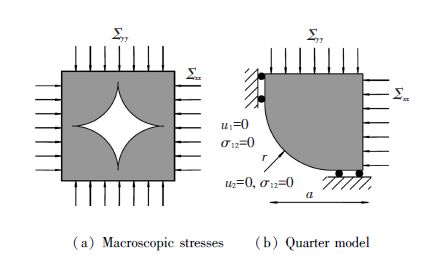
3.1 Yield Function Φ∞(Σ) of Rigid Plastic MaterialOne load case is involved in the part (Fig. 2(a)). Given the symmetry, the computation can be carried out on a quarter of the element with the boundary conditions as shown in Fig. 2(b). Different porosities, determined by the ratio of r and a, are considered during calculation and the hardening exponent p is valued 1.01(as shown in Table 1) .
| Table 1 Parameters of loading case 1 |
|
Figure 2 Boundary conditions |
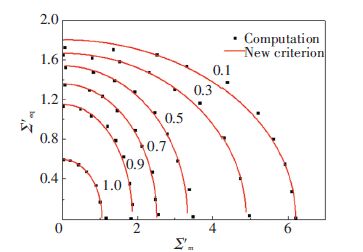
The numerical results represented with stresses Σ′eq and Σ′m under different values of r/a are shown in Fig. 3. According to the distribution of points, the elliptic fitting equation is adopted. Then new criterion function can be written as:
| ${{\Phi }_{\infty }}\left( \sum \right)={{\left( \frac{{{{{\sum }'}}^{2}}_{m}}{{{A}_{1}}{{\left( f \right)}^{2}}}+\frac{{{{{\sum }'}}^{2}}_{eq}}{{{B}_{1}}{{\left( f \right)}^{2}}} \right)}^{{1}/{2}\;}}$ | (14) |
where f stands for porosity depending on the ratio of r and a.
Parameters A1 and B1 are well approximated with
| $\left\{ \begin{array}{*{35}{l}} {{A}_{1}}\left( f \right)=-1.421-1.8121n\left( f+0.0126 \right) \\ {{B}_{1}}\left( f \right)=0.618-0.41n\left( f+0.05 \right)whenf<0.10515 \\ {{B}_{1}}\left( f \right)=-0.00212\exp \left( {f}/{0.03614}\; \right)+1.3957, otherwise \\ \end{array} \right.$ | (15) |
with 0.005 1≤f≤0.214 6.
The computation results and fitting curves are shown together in Fig. 3, which gives a good conformity.
|
Figure 3 Numerical results and yield surfaces under different values of r/a |
3.2 Macroscopic Potential Φq(Σ) of Norton-Hoff Material
Homogenization technique is based on integral approach, such as Eq.(9) . Then, according to macroscopic yield function for rigid plastic material Eq.(14) , Eq.(5) can be extended to macroscopic level and the macroscopic potential of Norton-Hoff material can be expressed as follows:
| ${{\Phi }_{q}}\left( \sum \right)=\frac{{{{\dot{\varepsilon }}}_{0}}{{\sigma }_{0}}}{q}{{\left( \frac{{{{{\sum }'}}^{2}}_{m}}{{{A}_{p}}{{\left( f \right)}^{2}}}+\frac{{{{{\sum }'}}^{2}}_{eq}}{{{B}_{p}}{{\left( f \right)}^{2}}} \right)}^{{q}/{2}\;}}$ | (16) |
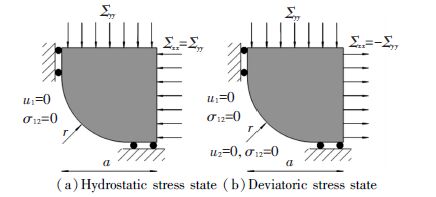
Parameters Ap and Bp are the function of porosity f and hardening exponent p(or q). In order to approximate Ap and Bp, two kinds of loading patterns are considered to REV, the states of purely hydrostatic stress and purely deviatoric stress (Fig. 4) . The values of porosity parameter r/a and hardening exponent p for calculation under the two states are listed in Table 2.
|
Figure 4 Boundary conditions for the quarter model |
| Table 2 Parameters of loading case 2 and case 3 |
Combining with Eq.(16) , Eq.(10) can be deduced as follows under the two cases respectively:
| $\frac{{{{\dot{E}}}_{m}}}{\sqrt{3}{{{\dot{\varepsilon }}}_{0}}}=\frac{{{{{\sum }'}}_{m}}^{q-1}}{A_{p}^{q}}$ | (17) |
| $\frac{{{{\dot{E}}}_{eq}}}{\sqrt{3}{{{\dot{\varepsilon }}}_{0}}}=\frac{{{{{\sum }'}}_{m}}^{q-1}}{B_{p}^{q}}$ | (18) |
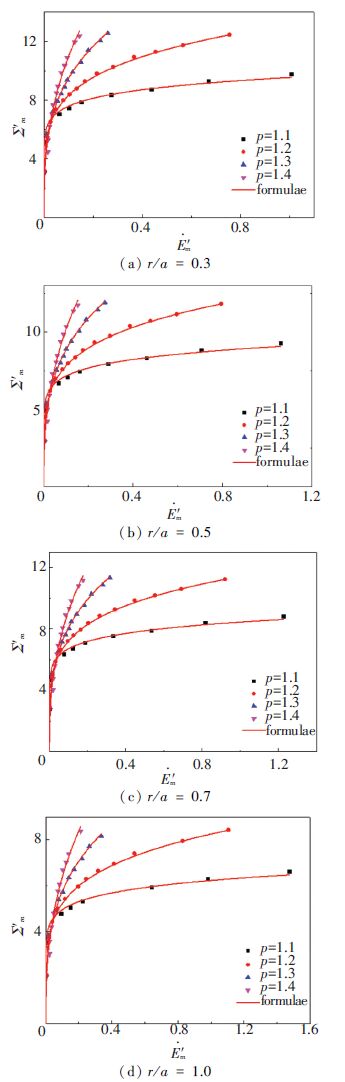
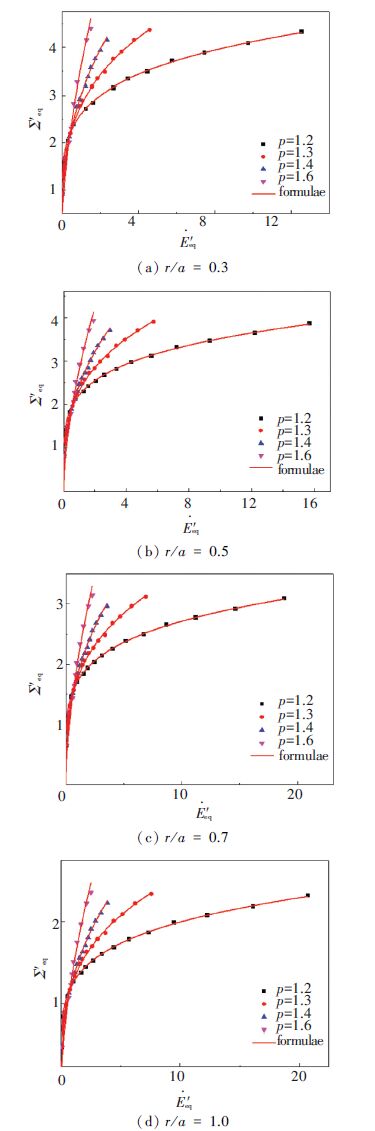
Numerical results of cases 2 and 3 are expressed with the curve of Σ′m-$\dot{E}$′m and Σ′eq-$\dot{E}$′eq respectively (Figs. 5 and 6) . And the variation of parameters Ap and Bp is well approximated with following formulations:
| $\left\{ \begin{array}{*{35}{l}} {{A}_{p}}\left( f \right)=\beta \left( 1+2.254p+1.322{{p}^{2}} \right)f, \\ \beta =\frac{-9.284+{{f}^{p-2.567}}}{{{\left( p-1.037 \right)}^{{5.958}/{p}\;}}} \\ {{B}_{p}}\left( f \right)=0.217\left[ 1-\left( 1.61-\frac{1.475}{\sqrt{p-1.187}} \right){{f}^{-0.475\left( \sqrt{p-3.081} \right)}} \right] \\ \end{array} \right.$ | (19) |
with 0.019 3≤f≤0.214 6, 1.2≤p≤1.6.
The results show the larger the p is, the faster the increasing of macroscopic stress is with macroscopic strain growing, which agrees with the mechanical meaning of hardening exponent in macroscopic level. By comparing the four pictures in Fig. 5 or Fig. 6, it is shown that when the porosity (determined by the value of r/a) is not large enough, its influence to the macroscopic constitutive laws as well as its correlation with p is not apparently.
|
Figure 5 Macroscopic mean stress vs. macroscopic mean strain rate for case 2 |
|
Figure 6 Macroscopic equivalent stress vs. macroscopic equivalent strain rate for case 3 |
4 Macroscopic Constitutive Laws Considering Pore Shape
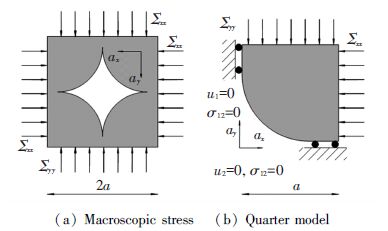
In the part, in order to explore the effect of pore shape on macroscopic constitutive laws, the pore shape parameter γ(valued by ax/ay) is involved and the porosity is set as a constant during numerical calculation. With the changing of parameter γ, circular particles turn into elliptic. The REV and boundary conditions for its quarter model are shown in Fig. 7.
|
Figure 7 Boundary conditions |
The loading case for approximating macroscopic yield function Φ∞(Σ)of rigid plastic material is shown in Table 3.
| Table 3 Parameters of loading case 4 |
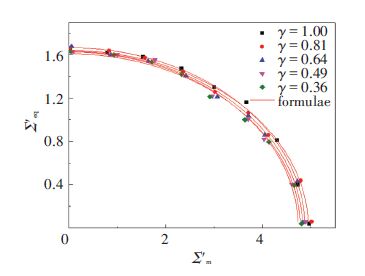
The numerical results represented by stresses Σ′eq and Σ′m under different pore shape are shown in Fig. 8. Parameters A1 and B1 in Eq.(14) are well approximated by:
| $\left\{ \begin{array}{*{35}{l}} {{A}_{1}}\left( \gamma \right)=4.914{{\gamma }^{0.034}} \\ {{B}_{1}}\left( \gamma \right)=1.588+0.0119{{e}^{-\frac{\gamma }{0.534}}} \\ \end{array} \right.$ | (20) |
with 0.36≤γ≤1.
Based on the computation results, new macroscopic yield surfaces under different pore shape are gotten (Fig. 8) , which represents with the decreasing of γ, the yield surface tends to cave in.
|
Figure 8 Numerical results and yield surfaces under different values of γ |
Two loading cases for approximating macroscopic potential Φq(Σ) of Norton-Hoff material are listed in Table 4.
| Table 4 Parameters of loading case 5 and case 6 |
Similar to loading cases 2 and 3, the numerical results of cases 5 and 6 are also expressed with the curve of Σ′m-$\dot{E}$′m and Σ′eq-$\dot{E}$′eq respectively. Then, parameters Ap and Bp in Eq.(16) is well approximated with the following formulations:
| $\left\{ \begin{array}{*{35}{l}} {{A}_{p}}\left( \gamma \right)=\beta \left( 1+8.04\gamma +25.48{{\gamma }^{2}} \right)\centerdot p, \\ \beta =\frac{-0.134+{{p}^{\gamma -7.03}}}{{{\left( \gamma +0.97 \right)}^{{-16.07}/{\gamma }\;}}} \\ {{B}_{p}}\left( \gamma \right)=7.51\centerdot \left[ 1-\left( 2.78-\frac{660}{\sqrt{\gamma +1.69}} \right){{p}^{-4.77\left( \sqrt{\gamma +14.06} \right)}} \right] \\ \end{array} \right.$ | (21) |
with 0.36≤γ≤0.81.
5 Effect of Secondary Cavities on Plastic BehaviorVoids in plastic porous medium are divided into two types. One is the main void and the other is the secondary cavities. In the part, the interaction between main and secondary voids is studied. Geometrical relationship of the two voids is shown in Fig. 9. Corresponding to voids, the medium is also divided into two scales, the micro-scale and macro-scale with the sizes of l and L respectively (l$ \ll $L). Secondary cavities are considered as distributing inside the particles while the main void results from regularly distribution of circle particles.
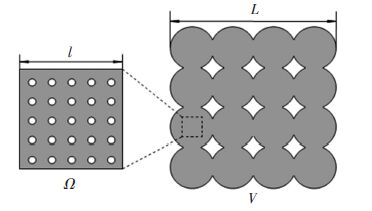
|
Figure 9 Two kinds of voids under different scale |
The micro-porosity fs is defined by the ratio of secondary cavities to Ω and the macro-porosity fl is defined by the ratio of main void to V. The REV containing secondary cavities and boundary conditions for its quarter model are shown in Fig. 10. During numerical calculation, two-scale voids are involved by defining the total porosity ft that is expressed as:
| ${{f}_{t}}={{f}_{s}}+{{f}_{1}}-{{f}_{s}}f$ | (22) |
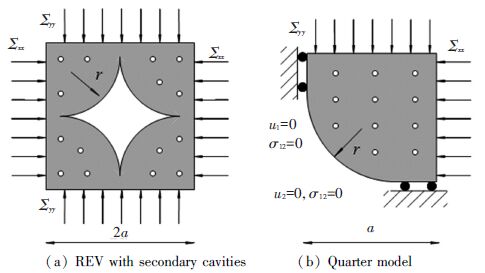
|
Figure 10 Boundary conditions |
Here, just macroscopic yield function for rigid plastic material is referred. Numerical calculation is performed with micro-porosity fs=0.01 and r/a=0.1, 0.3, 0.5, 0.7 in turn. Computation results represented by stress Σ′eq and Σ′m are shown in Fig. 11. The yield surface is still introduced by elliptic fitting function and for comparing, original yield surfaces not considering secondary cavities into account are presented together.
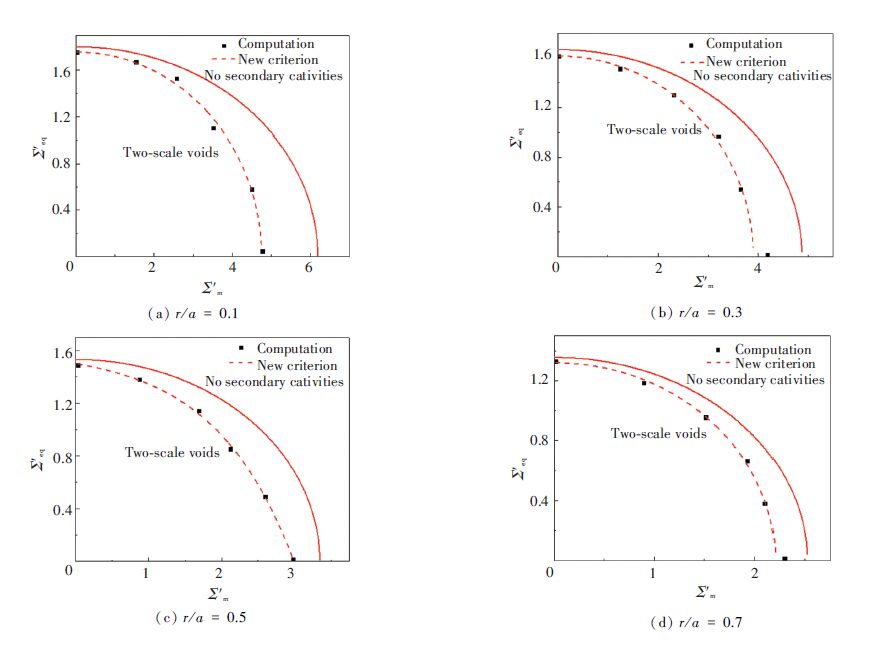
|
Figure 11 Yield surfaces with secondary cavities and without secondary cavities |
Compared with the original yield surface, the yield surface containing secondary cavities is contracted inward and the phenomenon is more noticeable when the macro-porosity is smaller. In addition, the higher the stress triaxiality ratio (Σm/Σeq) is, the greater the interaction between two-scale cavities is.
Similar to Eq.(14) , macroscopic yield function for the porous medium containing secondary cavities can be expressed as:
| $\Phi \left( \sum , {{f}_{s}}, {{f}_{1}} \right)={{\left( \frac{{{{{\sum }'}}^{2}}_{m}}{B{{\left( {{f}_{s}}, {{f}_{1}} \right)}^{2}}}+\frac{{{{{\sum }'}}^{2}}_{eq}}{A{{\left( {{f}_{s}}, {{f}_{1}} \right)}^{2}}} \right)}^{{1}/{2}\;}}$ | (23) |
For further study on the interaction between two-scale voids, parameters A and B related to the micro-porosity and macro-porosity are investigated. Numerical calculations are implemented with a series of value for micro-porosity fs and macro-porosity fl under two macroscopic stress states. One is the purely hydrostatic stress state (Σeq=0) , the other is purely deviatoric stress state (Σm=0) . Numerical results expressed by the curves of A-fs and B-fs are shown in Fig. 12.
Parameters A and B are well approximated by
| $\eqalign{ & \left\{ \matrix{ \alpha = fs + fl - 1.14fsf{l^{0.74}} + 1.64fsf{l^{ - 0.002}} \hfill \cr \beta = fs + fl - 4.05{(fsfl)^{0.5}} + 0.87{(fsfl)^{ - 0.07}}and \hfill \cr} \right. \cr & \left\{ \matrix{ {\rm{ }}0 \le fs \le 0.01 \hfill \cr 0.005{\rm{ }}1 \le fl \le 0.197{\rm{ }}7 \hfill \cr} \right. \cr} $ | (24) |
with
| $\eqalign{ & \left\{ \matrix{ \alpha = fs + fl - 1.14fsf{l^{0.74}} + 1.64fsf{l^{ - 0.002}} \hfill \cr \beta = fs + fl - 4.05{(fsfl)^{0.5}} + 0.87{(fsfl)^{ - 0.07}}and \hfill \cr} \right. \cr & \left\{ \matrix{ {\rm{ }}0 \le fs \le 0.01 \hfill \cr 0.005{\rm{ }}1 \le fl \le 0.197{\rm{ }}7 \hfill \cr} \right. \cr} $ |
From Fig. 12, compared with B, A is more dependent on micro-porosity when the size ratio r/a is smaller, which means parameter A is influenced more by micro-porosity when the macro-porosity is small. As to the yield criterion, the interaction between the main void and secondary cavities is more obvious under higher stress triaxiality ratio and lower macro-porosity.
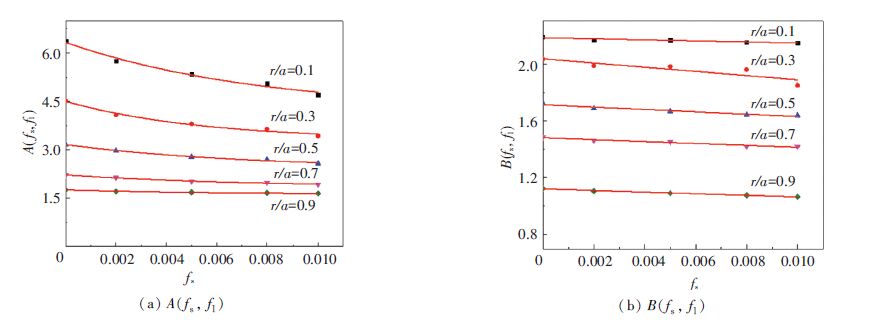
|
Figure 12 Variation of A (fs, fl) and B (fs, fl) |
6 Conclusions
Beginning with Von Mises yield function φ∞(σ) and Norton-Hoff stress potential φq(σ), the paper proposes a conception of macroscopic constitutive laws by homogenizing the stress potential within a macroscopic element (REV). Series of numerical calculation are performed for achieving the macroscopic yield function Φ∞ and macroscopic stress potential Φq. Further, the pore shape and two-scale voids are taken into account. All the results are concluded as follows:
1) In macroscopic level, the hardening exponent p functions similarly to the way in microscopic level.
2) The variation of porosity affects macro-constitutive relation less obviously unless the porosity is large enough.
3) Macroscopic yield surface has an inclination to indent with the decreasing γ.
4) The interaction between two-scale voids is more obvious when stress triaxiality ratio is higher and macro-porosity is lower.
The problem discussed in the paper just remains in plain strain and the porous medium is regarded as ideal periodically in geometry. Actually, some factors, like particle size and boundary conditions, are indeterminate. So in further study, stochastic analysis should be involved.
| [1] |
Rice J R, Tracey D M. On the ductile enlargement of voids in triaxial stress fields.
Journal of the Mechanics and Physics of Solids, 1969 , 17 : 201-217.
DOI:10.1016/0022-5096(69)90033-7 ( 0) 0)
|
| [2] |
Gurson A L. Continuum theory of ductile rupture by void nucleation and growth: Part 1-Yield criteria and flow rules for porous ductile medias.
Journal of the Engineering Materials and Technology, 1977 , 99 : 2-15.
DOI:10.1115/1.3443401 ( 0) 0)
|
| [3] |
Xia L, Shih C F, Hutchinson W J. A computational approach to ductile crack growth under large scale yielding conditions.
Journal of the Mechanics and Physics of Solids, 1995 , 43 (3) : 389-413.
DOI:10.1016/0022-5096(94)00069-H ( 0) 0)
|
| [4] |
Guennouni T, Francois D. Constitutive equations for rigid plastic or viscoplastic materials containing voids.
Fatigue and Fracture of Engineering Materials and Structures, 1987 , 10 (5) : 399-418.
DOI:10.1111/ffe.1987.10.issue-5 ( 0) 0)
|
| [5] |
Garajeu M, Suquet P. Effetcive properties of porous ideally plastic or viscoplastic materials containing rigid particles.
Journal of the Mechanics and Physics of Solids, 1992 , 45 (6) : 873-902.
( 0) 0)
|
| [6] |
Danas K, Idiart M I, Ponte P, et al. A homogenization-based constitutive model for isotropic viscoplastic porous media.
International Journal of Solids and Structures, 2008 , 45 (11) : 3392-3409.
( 0) 0)
|
| [7] |
Fritzen F, Forest S, Bohlke T, et al. Computational homogenization of elasto-plastic porous metals.
International Journal of Plasticity, 2012 , 29 : 102-119.
DOI:10.1016/j.ijplas.2011.08.005 ( 0) 0)
|
| [8] |
Flandi L, Leblond J B. A new model for porous nonlinear viscous solids incorporating pore shape effetcs-I: Theory.
European Journal of Mechanics-A/Solids, 2005 , 24 (4) : 537-551.
DOI:10.1016/j.euromechsol.2005.03.003 ( 0) 0)
|
| [9] |
Julien J, Garajeu M, Michel J C. A semi-analytical model for the behavior of saturated viscoplastic materials containing populations of voids of different sizes.
International Journal of Solids and Structures, 2011 , 48 (10) : 1485-1498.
DOI:10.1016/j.ijsolstr.2011.01.031 ( 0) 0)
|
| [10] |
Danas K, Aravas N. Numerical modeling of elasto-plastic porous materials with pore shape effects at finite deformations.
Composites Part B: Engineering, 2012 , 43 (6) : 2544-2559.
DOI:10.1016/j.compositesb.2011.12.011 ( 0) 0)
|
| [11] |
Kailasam M, Castañeda P P. The evolution of anisotropy in porous materials and its implications for shear localization. IUTAM Symposium on Mechanics of Granular and Porous Materials.
Kluwer Academic Publishers, 1997 : 365-376.
( 0) 0)
|
| [12] |
Kailasam M, Castañeda P P. A general constitutive theory for linear and nonlinear particulate media with microstructure evolution.
Journal of the Mechanics and Physics of Solids, 1998 , 46 (3) : 427-465.
DOI:10.1016/S0022-5096(97)00095-1 ( 0) 0)
|
| [13] |
Guennouni T, Francois D. Influence of the pore morphology and secondary cavities on the plastic behavior of porous materials.
Fatigue and Fracture of Engineering Materials and Structures, 1988 , 11 (4) : 267-276.
DOI:10.1111/ffe.1988.11.issue-4 ( 0) 0)
|
| [14] |
Li G C, Guennouni T, Francois D. Influence of secondary void damage in the matrix material around voids.
Fatigue and Fracture of Engineering Materials and Structures, 1989 , 12 (2) : 105-122.
DOI:10.1111/ffe.1989.12.issue-2 ( 0) 0)
|
| [15] |
Fabregue D, Pardoen T. A constitutive model for elastoplastic solids containing primary and secondary voids.
Journal of the Mechanics and Physics of Solids, 2008 , 56 (3) : 719-741.
DOI:10.1016/j.jmps.2007.07.008 ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23


