With the rapid development of Internet and the growing popularity of computers, student achievement management system in colleges and universities has been widely adopted and greatly enhanced the level of student management. However, this process also raises a number of problems. For example, the information stored in the management system is simple and raw, while most colleges and universities are still using conventional methods of analysis such as sorting, averaging, and looking extremum to process these data, this method cannot find the potential association among the data. Discovering useful knowledge in those raw data, which provides a useful reference for teaching management work has become a serious problem in the field.
Data mining refers to searching for hidden knowledge in large amounts of data through algorithms. Through data mining techniques, we can find potential relationships, rules and trends in data. As the data accumulate more and more quickly, demand for efficient, in-depth data analysis methods is increasingly urgent. In this context, data mining technology has received more and more attention, corresponding research results are also increasing rapidly. Data mining technology combines many areas of theories and techniques such as statistics and data visualization techniques, artificial intelligence, technique of database, machine learning, pattern recognition and so on. The main methods of data mining technology include statistical analysis and visualization, clustering (clustering, outlier analysis), forecasting (classification, regression, time series analysis), relationship mining (association rule mining, sequential pattern mining, Related mining), text mining and so on. It also involves a wide range of algorithms such as decision tree, neural network, Bayesian network, artificial intelligence, inheritance algorithm, correlation analysis and so on. Commercial software based on data mining techniques are also widely used, such as IBM's Intelligent Miner for Data, Microsoft's SQL Server Analysis Services, SPSS Clementine, SAS Enterprise Miner and so on[1-4].
As a branch of data mining, educational data mining is mainly used in the field of education, it has a very wide range of application in student achievement management. With the introduction of office automation system in education industries, accumulation of data on education system is increasing. It's proved an urgent demand that excavating effective information from these original educational data and using this information to guide education work and improve the quality of education management. Therefore, it's extremely important to develop a series of accurate and reliable educational data mining models and promote these models practically.
However, applications of educational data mining also have a number of disadvantages. Now, many researches on educational data mining at home and abroad are still staying in validating the performance of the most basic models which are far from practical. In addition, the basic models' performance is not ideal, which causes using a single basic model cannot complete data mining work well. Moreover, there is no universal educational data mining system for use by the education industries now, which, to some extent, impedes the application of educational data mining technology in the management of school teaching.
This paper focuses on the current educational data mining models, which are not only the improvement of the conventional model but also the perfect integration of them, they are more superior and comprehensive in performance, thus, they have a very broad prospects for practice in the area of educational data mining.
2 Progress on Educational Data Mining ModelsAs a branch of data mining, educational data mining is still in its infancy stage. On the basis of the existing document, this article organizes and summarizes four research results which are universal relatively.
2.1 New York Institute of Technology's “Student At-Risk Model” (STAR)Based on historical data, this model can predict the student who is in a big academic risk, and it can also distinguish the key factors leading students at academic risk and assist the teaching staff in intervening this group of students to reduce their risk of dropping out early. The system based on STAR is user friendly, and its output can be understood and accepted by most of the teaching staff. With high efficiency, it can complete the work ranging from data collection to the predictive tasks automatically, which provides great convenience for the management work of the teaching staff.
New York Institute of Technology's Work began from the Autumn of 2012 and had gone through three stages totally.
The first stage(STAR 1.0) : Freshmen's information such as admission achievement information, placement test scores and so on were collected and compiled in one Excel sheet. Then their information was scored and finally were summed in order to determine whether the student is in academic risk. This approach was highly problematic because students' information needs to be collected manually, and it was time-consuming and its outputs were unconvincing. So, this method was abandoned quickly.
The second stage(STAR 2.0) : Setting up data set in the database and using data mining tools to carry out classification and prediction tasks, the selected data mining tool is SQL Server Analysis Services (SSAS) which is a part of Microsoft SQL Server. Neural network algorithm, Bayesian network, logistic regression analysis, decision tree model can be performed in SSAS. The data SSAS need was collected when students were registering. Different from the information collected in the first stage, students' economic information was added in the second stage[5]. In the actual operation, the models above were performed separately. By comparing the results of prediction with the actual situation, the Logistic regression was selected as initial model because it had the highest predictive accuracy in this situation. Furthermore, the return of the initial model and students' data were integrated. Finally, data mining work was completed in this stage. Some experiments were conducted to test the performance of STAR 2.0 and the results are shown in Table 1[6].
| Table 1 Ensemble model validation |
The third stage: the actual software system was established on the base of the prediction model in the second stage and students' data. This academic risk prediction system was “point to point” (means “from students' data to prediction results”, as shown in Fig. 1[6]). The results of data mining were reported by SQL Server Reporting Services (SSRS) which provide a useful reference for school teaching management staff. This system is user-friendly and has been warmly welcomed by the school teaching management staff.

|
Figure 1 The working schematic of STAR |
2.2 A Synthesis of Latent-factor and Knowledge Tracing Models (LF-KT)
This model was proposed by Mohammad and Khajah [7]and the study of it is still in its initial stage. The main feature of LF-KT is that it can infer students' knowledge level according to their situations of solving problems. LF-KT consists of two basic models: Latent-factor model and knowledge tracing model[8]. Both models have their own advantages and disadvantages in different application environments. After integrating two basic models above, LF-KT has a higher predictive accuracy and a wider range of use. More importantly, basic models' features can be reflected by changing LF-KT's parameters.
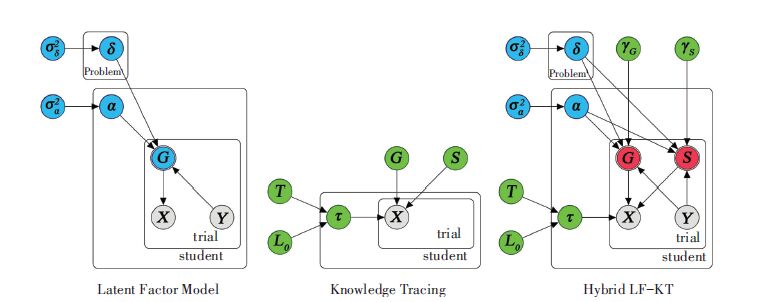
As is shown in Fig. 2[7], LFM and BKT are depicted in a manner that allows the two models to be superimposed to obtain a synthesis, which was so-called LF-KT. LF-KT personalizes the guess and slip probabilities based on student ability and problem difficulty[7]:
| $log~it({{G}_{si}}|{{Y}_{is}}=y)={{\alpha }_{s}}-{{\delta }_{y}}+{{\gamma }_{G}}$ | (1) |
and
| $log~it({{S}_{si}}|{{Y}_{is}}=y)={{\delta }_{y}}-{{\alpha }_{s}}+{{\gamma }_{S}}$ | (2) |
Where E[αs]=0, E[δy]=0, αs~N(0, σ22) and δy~N(0, σ22), σ22 and σ22 are variances drawn from an Inverse-Gamma-distributed conjugate prior. LFKT can be specialized to the LFM simply byfixing T=0 and L0=0. It can be also specialized to BKT at the limit of σ22, σ22→0[7].
|
Figure 2 Graphical model depiction of the latent-factor model (left), knowledge tracing model (middle) and LF-KT model (right) |
Compared to the basic model (LFM and KT), the biggest improvement of LF-KT is that it personalizes the guess and slip probabilities based on student ability and problem difficulty. In the training of the model, each component of LF-KT will be trained simultaneously because only in this way the transition in the knowledge state may become sharper and a better measure of problem difficulty and student ability may be obtained.
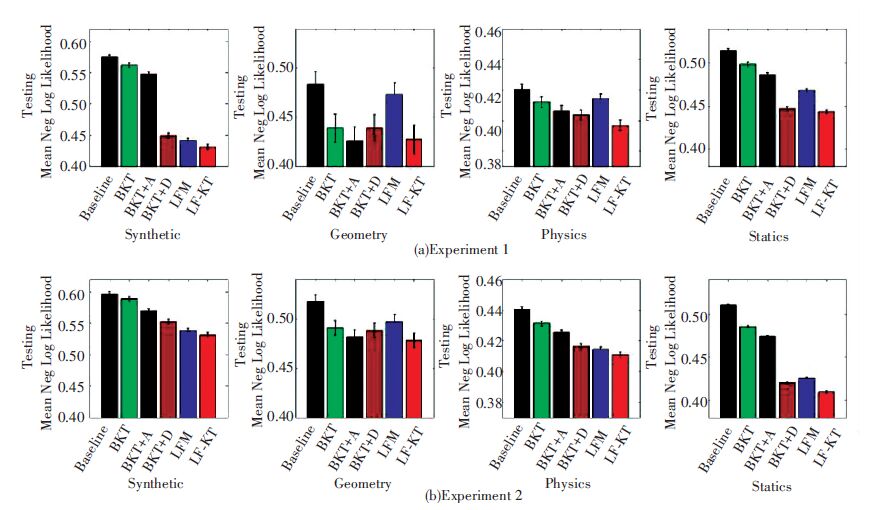
In order to prove the efficiency of LF-KT, two experiment [7] (Predicting Performance of Current Students and Predicting Performance of New Students) were conducted. The results are as follows:
In Fig. 3[7], the horizontal axis refers to the different model and the vertical axis refers to the mean negative log likelihood on the test data where smaller scores indicate better performance. It is proved that LF-KT has a better performance than LFM, BKT and its variants.
|
Figure 3 The result of two experiments |
However, LF-KT has an obvious shortcoming:the efficiency of its algorithm is low and for this reason the execution time is long. Under the same test conditions, LF-KT's execution time is longer than the sum of the execution times of the two component models. So, in the future the execution time of LF-KT should be optimized in order to put it into practice. However, with significantly enhancement of computer hardware's performance in recent years, LF-KT is still an advanced, effective model with the help of high performance computer.
2.3 “Logistic Regression in Dynamic Bayes Net” Model (LR-DBN)LR-DBN was first proposed by Carnegie Mellon University's researchers Yanbo Xu and Jack Mostow[9-11] in 2011.
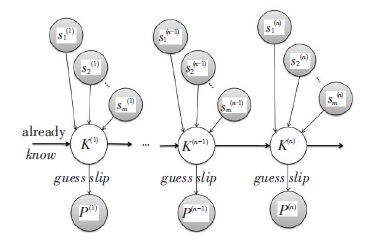
Like standard KT, LR-DBN (as shown in Fig. 4[9]) represents the knowledge for step n as a hidden knowledge state K(n) in a dynamic Bayes net. However, LR-DBN adds a layer of observable states Sj(n) as indicator variables to represent whether step n involves subskill j:1 if so, 0 if not. LR-DBN uses logistic regression to model the initial hidden knowledge state at step 0 and the transition probabilities from step n-1 to n as follows[9]:
| $P(not~{{K}^{\left( 0 \right)~}})=\frac{exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\beta }_{j}}^{\left( 0 \right)~}{{S}_{j}}^{\left( 0 \right)~})}{1+exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\beta }_{)}}^{\left( 0 \right)~}{{S}_{)}}^{\left( 0 \right)~})}$ | (3) |
| $P(not~{{K}^{(n)}}|not~{{K}^{\left( n-1 \right)~}})=\frac{exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\beta }_{j}}{{S}_{j}}^{(n)})}{1+exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\beta }_{j}}{{S}_{j}}^{(n)})}$ | (4) |
| $P(not~{{K}^{(n)}}|not~{{K}^{\left( n-1 \right)~}})=\frac{exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\gamma }_{j}}{{S}_{j}}^{(n)})}{1+exp(-\underset{j=1}{\overset{m}{\mathop{\sum }}}\, {{\gamma }_{j}}{{S}_{j}}^{(n)})}$ | (5) |
|
Figure 4 Graphical model depiction of LR-DBN |
These three conditional probabilities for each subskill replace the KT knowledge parameters already know, learn, and forget, but LR-DBN retains KT's guess and slip parameters at each step[9].
Unlike conventional knowledge tracking model, LR-DBN can trace multiple subskills of students without considering their independency, which can combine multiple subskills together more flexibly. LR-DBN uses Expectation Maximization (EM) to fit parameters for multiple subskills simultaneously and uses logistic regression to model the transition probabilities between knowledge states, as well as the relation of the knowledge state at each step to the subskills it involves. In terms of performance, LR-DBN's predictive accuracy is higher than knowledge tracing model and some other models. When performing the same scale prediction task, the number of parameters used in LR-DBN is less than some other models. Most importantly, LR-DBN is publicly available now because it has been added to the Bayes Net Toolkit for Student Modeling (BNT-SM) which is an open-source Matlab package that supports many learning and inference algorithms for both static and dynamic Bayes models. This undoubtedly creates the conditions for the promotion and application of LR-DBN.
To compare LR-DBN to previous methods for tracing multiple subskills, seven models were fitted to real data: LR-DBN, LR-DBN Minus, CKT, and three variants of standard KT(“full responsibility, ” “blame weakest, credit rest, ” and “update weakest subskill”), with majority class as an additional baseline[9]. The results are shown in Table 2.
| Table 2 Mean per-student accuracy on Reading Tutor data(95% confidence interval in parentheses) |
All seven methods' binary predictive accuracies on the test data are listed in Tables 2 and 3[9]. However, compared to the previous models, although LR-DBN can trace multiple subskills better, it must be told which steps use which subskills. So, the automation of this process may be an important research direction in the future work. In addition, the execution time of LR-DBN is so long that it may be an obstacle which will hinder the pace of its practice.
2.4 Feature Aware Student Knowledge Tracing Model(FAST)FAST, a model which is effective and innovative, was proposed by José González-Brenesy et al[12]. Recently, FAST allows integrating general features into Knowledge Tracing. Compared to traditional knowledge tracking models and its variants (as shown in Fig. 5[12]), FAST can greatly improve classification performance, so it can achieve higher accuracy in predicting student performance.
In parameter learning, FAST uses the Expectation Maximization with Features algorithm[13], where the parameters λ are a function of weights β and features f(t). The feature extraction function f constructs the feature vector f(t) from the observations (rather than student responses) at the tth time step. For example, the emission probability is represented with a logistic function:
| $\begin{align} & \lambda {{\left( \beta \right)}^{y\prime , k\prime }}=p\left( y=y\prime |k=k\prime ;\text{ }\beta \right)= \\ & \frac{1}{1\text{ }+exp(-{{\beta }^{T}}\cdot f\left( t \right))} \\ \end{align}$ |
| Table 3 Mean per-student accuracy on Algebra Tutor data(95% confidence interval in parentheses) |

|
Figure 5 Plate diagrams of the Knowledge Tracing and its variants |
The parameter β is got from data by training a weighted regularized logistic regression using a gradient-based search algorithm[12].
FAST(as shown in Fig. 6[12]) is an integrated and comprehensive model. By design, it can represent Knowledge Tracing model and its variants. FAST uses logistic regression parameters for the guess, slip and learning probabilities, its performance is linear in the number of features. In parameter learning process, FAST uses the Expectation Maximization with Features algorithm-a modification of the original Expectation Maximization (EM) algorithm. FAST allows three different types of features: (i) features that are active only when students have mastered the skill, (ii) features that are active only when students have not mastered the skill, (iii) features that are always active. In the process of constructing a FAST model, the effect of subskills is considered and in conventional Knowledge Tracing model these subskills are not to be taken into account. FAST's good performance is considered to be a result of fully taking into account the effect of subskills in logistic regression.

|
Figure 6 Plate diagrams of FAST |
In the train of the logistic regression, the instance weight is:
| ${{w}_{y\prime , k\prime }}=p\left( k=k\prime |Y;\beta \right)$ | (7) |
Then, the Maximum Likelihood estimate β* is:
| ${{\beta }^{*}}=\underset{\beta }{\mathop{argmax}}\, \underbrace{\underset{y, k}{\mathop{\sum }}\, ({{w}_{y, k}}\cdot log\lambda {{\left( \beta \right)}^{y, k}}}_{data\text{ }fit}-\underbrace{\kappa \|\beta {{\|}_{2}}^{2}}_{regularization}$ | (8) |
Some experiments have been conducted to prove the superior performance of FAS, Table 4[12] compares FAST with different models previously used in the literatures, and the evaluation criterion of the performance was overall AUC. From the results we can see that FAST significantly outperforms all the above Knowledge Tracing variants, PFA and LR-DBN.
| Table 4 Overall AUC for multiple subskills experiments |
FAST's another feature is that its execution time is very short: when performing the task which has 15 500 data points, LR-DBN takes about 250 min while FAST only takes about 44 s. The reason is that FAST's execution time increases linearly as the number of features grows, therefore, FAST has a high practical value.
In addition, FAST has a high level of versatility, which can be applied in the following three important cases: (i) modelling subskills; (ii) incorporating IRT (Item Response Theory) features in Knowledge Tracing; (iii) using features designed by experts. FAST has a high flexibility in use, it is extremely effective in fitting with the inference process.
2.5 Summary of the Models AboveThrough the analysis of the models above, it is easy to find out that each model has its advantages and disadvantages. Different model has different features such as efficiency, comprehensiveness, ease of use, stability and so on. Different features make them apply to different occasions. Therefore, the model which can be really applied to educational data mining problem should be studied further.
3 The Computational Example of Artificial Neural Networks 3.1 An Introduction to Artificial Neural Networks AlgorithmsArtificial neural network is not a kind of special education data mining model. It appeared earlier in the education concept of data mining. However, it is a powerful tool for education data mining, which has received the widespread attention in recent years[14].
Artificial neural networks is a system capable of learning and summary, which can carry on the training by known data and, use the existing historical data to estimate the current data[15]. Artificial neural networks are like a man with a simple decision ability and judgment. It can produce an automatic identification system through to the local data comparing. Because of this, the artificial neural networks algorithm is sometimes more accurate than logical reasoning and calculus.
BP neural network and its variations are used regularly in the practical application of artificial neural network. BP neural network is a multilayer neural network, named by using BP algorithm. BP neural network is usually composed of input layer, output layer and several hidden layers, and each layer has many nodes, and each node is a neuron, and the upper and lower nodes are connected by the weight, nodes between layer and layer adopts the way of full connection, meanwhile there is no link between nodes in each layer[16]. Taking a BP neural network which has an input layer, an output layer and a hidden layer as an example, its structure is shown in Fig. 7.

|
Figure 7 Structure of BP neural network which have three layers |
Artificial neural networks algorithm has many advantages compared with other algorithms in some ways, such as association rules algorithm in noisy data, redundancy of information, under the condition of incomplete data or data sparse[17]. And the artificial neural networks due to its good organizational adaptability, parallel processing, distributed storage, high fault tolerance, can play good effects[18-19]. The algorithm of artificial neural network has been written into the package, the user need not know the details of the algorithm and use it directly to perform tasks such as prediction, recognition[20]. This undoubtedly brings great convenience for practical promotion.
In view of the current education and the research status of data mining and the actual situation of China, we choose artificial neural networks which is most likely to be promoting practice and use it to perform data mining tasks, and the operation of the algorithm is carried out in MATLAB neural network toolbox.
3.2 Data SelectionTo train the BP neural network, we must prepare the training sample[21-22]. As shown in Table 5, part of some students' course grades which seems to have stronger relevance are extracted for neural network prediction model of training and testing.
| Table 5 Part of some students' course grades |
3.3 Perform the Task and Analysis the Results
Perform the BP neural network algorithm in MATLAB neural network toolbox, and the results are shown in Table 6.
| Table 6 The results |
When the neural network learning coefficient is set to 0.01, number of hidden layer nodes is 20, after 10 000 times training cycle, it is concluded that the data in Table 6. It can be seen that in addition to the part of data, the rest of the deviations are small, achieving an ideal effect.
4 ConclusionsWith the increase of big data, the data mining technology is valued more and more. Although the research of data mining is already quite rich and many universal data mining tools have also been developed now, the application of data mining technology in university teaching management system is still very rare. In order to improve the teaching quality and working efficiency of teaching management staff, it is necessary to select the educational data mining models whose performance is superior and develop simple, efficient data mining system applicable to university teaching management system which is on base of these models. This is also a promising direction in the development of teaching management system in colleges and universities.
| [1] |
Jiang Hao, Zhou Xiaoyan. The application of data mining technology in educational management system. Proceedings of 2011 National Conference on Electronic Information Technology and Application. Shanghai: Shanghai Higher Vocational Education Steering Committee of Electronic Information, 2011.798-801. (In Chinese)
( 1) 1)
|
| [2] |
Wang Guanghong, Jiang Ping. Survey of data mining.
Journal of Tongji University, 2004 , 32 (2) : 246-252.
( 1) 1)
|
| [3] |
Liang Xun. Data mining: Modeling, algorithms, applications and systems.
Computer Technology and Development, 2006 , 16 (1) : 1-65.
( 1) 1)
|
| [4] |
Xie Shaoqun. Data Mining Based on the XML and its Applications of Customer Relationships Management of E-commerce.
Guangzhou: South China University of Technology, 2008 .
( 1) 1)
|
| [5] |
Rong Chen, Desjardins Stephen L. Exploring the effects of financial aid on the gap in student dropout risks by income level.
Research in Higher Education, 2008 , 49 (1) : 1-18.
DOI:10.1007/s11162-007-9060-9 ( 1) 1)
|
| [6] |
Lalitha Agnihotri, Alexander Ott. Building a Student At-Risk Model: An End-to-end Perspective. Proceedings of the Seventh International Conference on Educational Data Mining. London: International Educational Data Mining Society, 2014.209-212.
( 2) 2)
|
| [7] |
Khajah M M, Wing R M, Lindsey R V, et al. Integrating latent-factor and knowledge-tracing models to rredict individual differences in learning. Proceedings of the Seventh International Conference on Educational Data Mining. London, UK: International Educational Data Mining Society, 2014.99-106.
( 6) 6)
|
| [8] |
Xu Yanbo, Mostow Jack. Using item response theory to refine knowledge tracing. Proceedings of the 6th International Conference on Educational Data Mining. Memphis, Tennessee:International Educational Data Mining Society, 2013.356-357.
( 1) 1)
|
| [9] |
Xu Yanbo, Mostow J. Comparison of methods to trace multiple subskills: Is LR-DBN best? Proceedings of the 5th International Conference on Educational Data Mining.
Chania: International Educational Data Mining Society, 2012 : 41-48.
( 6) 6)
|
| [10] |
Xu Yanbo, Mostow J. Using logistic regression to trace multiple subskills in a dynamic bayes net. Proceedings of the 4th International Conference on Educational Data Mining. Eindhoven: International Educational Data Mining Society, 2011.241-245.
( 1) 1)
|
| [11] |
Xu Yanbo, Mostow J. Logistic regression in a dynamic bayes net models multiple subskills better! Proceedings of the 4th International Conference on Educational Data Mining.
Eindhoven: International Educational Data Mining Society, 2011 : 337-338.
( 1) 1)
|
| [12] |
González-Brenes J, Huang Y, Brusilovsky P. General features in knowledge tracing: Applications to multiple subskills, temporal item response theory, and expert knowledge. Proceedings of the Seventh International Conference on Educational Data Mining. London: International Educational Data Mining Society, 2014.84-91.
( 5) 5)
|
| [13] |
Berg-Kirkpatrick T, Bouchard-Côté A, De Nero J, et al. Painless unsupervised learning with features. Human Language Technologies: The 2010 Annual Conference of the North American Chapter of the Association for Computational Linguistics. Los Angeles: The Association for Computational Linguistics, 2010.582-590.
( 1) 1)
|
| [14] |
Hecht Nielson R. Neurocomputing.
Upper Saddle River: Addison Wesley, 1990 : 593-608.
( 1) 1)
|
| [15] |
Matthew Zeidenberg. Neural Networks in Artificial Intelligence.
Chichester: Ellis Horwood Limited, 1990 : 32-36.
( 1) 1)
|
| [16] |
Luo Chenghan. Realization of BP network based on neural network tool kit in MATLAB.
Computer Simulation, 2004 , 21 (5) : 109-115.
( 1) 1)
|
| [17] |
Churing Y. Backpropagation, Theory, Architecture and Applications.
New York: Lawrence Erbaum Pulishers, 1995 : 115-155.
( 1) 1)
|
| [18] |
Wang Kaicheng. Academic Warning of College Students Based on Data Mining. Shanghai: Shanghai Normal University. 2012. (In Chinese)
( 1) 1)
|
| [19] |
Saumya Bajpai, Kreeti Jain, Neeti Jain. Artificial Neural Networks.
International Journal of Soft Computing and Engineering, 2011 , 1 .
( 1) 1)
|
| [20] |
Howard Demuth, Mark Beale. Neural Network Toolbox User's Guide. The Mathworks, Inc., 1994.
( 1) 1)
|
| [21] |
Han C Y, Wang Y Y, Zhang F. Correction model of the NTC thermistors based on neural network.
Electronic Measurement Technology, 2013 , 36 (9) : 5-8.
( 1) 1)
|
| [22] |
Zhu Jianmin, Shen Zhengqiang, Li Xiaoru, et al. Magnetic levitation ball position control based on neural network feedback compensation control.
Chinese Journal of Scientific Instrument, 2014 , 35 (5) : 976-986.
( 1) 1)
|
 2016, Vol. 23
2016, Vol. 23



