2. Shanghai Institute of Spaceflight Control Technology, Shanghai 200233, China ;
3. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 200233, China
In recent years, on-orbit operation is an important research direction in space missions, such as rendezvous and docking, on-orbit maintenance and capturing space targets. When spacecraft conducts space operations, the motion of system components or the spacecraft three-axis attitude movement will cause the system inertial parameters to change over time, which make the whole dynamical system strongly coupled and nonlinear. Furthermore, capturing space targets, especially uncooperating targets, will result in a coupling system with model uncertainty.
Previous scholars have researched many control methods for this special controlled object, such as active disturbance rejection control[1-2], sliding mode control[3-5], neural network control[6], fuzzy control[7], etc. Active disturbance rejection control and sliding mode control can deal with control systems with parameter uncertaintiy without precise modeling, but they all need the knowledge of dynamic relationship between model parameters or the nominal value of uncertain parameters. In neural network control, network nodes and hidden layer settings need a part of information about the controlled object. For general fuzzy control, the selection of membership functions and fuzzy rules need a deep understanding of the controlled object, which cannot be changed once they are established. When the object information is totally unknown, all the control methods mentioned above can hardly meet the control requirements.
Although it is hard to acquire the information of spacecraft model, a mass of system input and output (spacecraft attitude angle, angular velocity, and control torque, etc.) data has been generated in the process of on-orbit operation, which contains all information about the system. It is significant to conduct effective control on system through the input and output data when it is unable to get accurate system model. Model-free adaptive control (MFAC)[8] refers to the method in which the designing of controller uses only the input and output data of controlled system and does not contain any information of dynamic model. MFAC is aiming at avoiding that the controller design is dependent on the mathematical model of system. This method has been widely used in chemical industry[9-10], power system[11], mechanical engineering[12-14], traffic[15-16] and other fields, but still has no specific application in the field of astronautics.
Spacecraft attitude control system is a typical multiple input multiple output (MIMO) system with different input and output dimensions. Since MFAC control method for MIMO system generally requires input and output with the same dimension, an augmented system with the same dimension input and output is constructed by introducing a dimension reduction matrix in this paper, which will make the application of MFAC in spacecraft attitude control system aptly. Numerical simulations are conducted on spacecraft attitude control system with time-varying model parameters. The results show that MFAC achieves a better controller performance than PD control.
2 Spacecraft Dynamical EquationFor simplicity, single rigid body spacecraft is discussed in this paper. The attitude of spacecraft is described by quaternion. The components of spacecraft angular velocity in body-fixed coordinate system can be describe as {ω}b = [ωxb, ωyb, ωzb]T. Then a virtual quaternion is introduced as
| ${{\Omega }_{b/0}}={{\omega }_{xb}}{{i}_{0}}+{{\omega }_{yb}}{{j}_{0}}+{{\omega }_{zb}}{{k}_{0}}$ |
The attitude motion equation of spacecraft can be written as
| $\dot{Q}=\frac{1}{2}Q\cdot {{\Omega }_{b/0}}$ | (1) |
where Q=[q0, q1, q2, q3]T is the attitude quaternion of the spacecraft body-fixed coordinate system with respect to the inertial coordinate system. Eq.(1) can be written in matrix form as
| $\left[ \begin{matrix} {{{\dot{q}}}_{0}} \\ {{{\dot{q}}}_{1}} \\ {{{\dot{q}}}_{2}} \\ {{{\dot{q}}}_{3}} \\ \end{matrix} \right]\text{=}\frac{1}{2}\left[ \begin{matrix} 0 & -{{\omega }_{xb}} & -{{\omega }_{yb}} & -{{\omega }_{zb}} \\ {{\omega }_{xb}} & 0 & {{\omega }_{zb}} & -{{\omega }_{yb}} \\ {{\omega }_{yb}} & -{{\omega }_{zb}} & ~0 & {{\omega }_{xb}} \\ {{\omega }_{zb}} & {{\omega }_{yb}} & -{{\omega }_{xb}} & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{q}_{0}} \\ {{q}_{1}} \\ {{q}_{2}} \\ {{q}_{3}} \\ \end{matrix} \right]$ | (2) |
The angular momentum of spacecraft is
| $H=I\omega $ |
where I is the inertia matrix of spacecraft.
Then the dynamic equation of spacecraft attitude motion can be expressed as
| $\frac{\text{d}H}{\text{d}t}=\frac{\text{d}\left( I\omega \right)}{\text{d}t}=M$ | (3) |
where M stands for the control torque.
Projecting Eqs.(3) into the body-fixed frame, yields
| $\begin{align} & \left[ \begin{array}{*{35}{l}} {{I}_{x}} & -{{I}_{xy}} & -{{I}_{xz}} \\ -{{I}_{yz}} & {{I}_{y}} & -{{I}_{yz}} \\ -{{I}_{zx}} & -{{I}_{zy}} & ~{{I}_{z}} \\ \end{array} \right]\left[ \begin{matrix} {{{\dot{\omega }}}_{xb}} \\ {{{\dot{\omega }}}_{yb}} \\ {{{\dot{\omega }}}_{zb}} \\ \end{matrix} \right]+\left[ \begin{array}{*{35}{l}} 0 & -{{\omega }_{zb}} & {{\omega }_{yb}} \\ {{\omega }_{zb}} & 0 & -{{\omega }_{xb}} \\ -{{\omega }_{yb}} & {{\omega }_{xb}} & 0 \\ \end{array} \right]. \\ & \left[ \begin{array}{*{35}{l}} {{I}_{x}} & -{{I}_{xy}} & -{{I}_{xz}} \\ -{{I}_{yz}} & {{I}_{y}} & -{{I}_{yz}} \\ -{{I}_{zx}} & -{{I}_{zy}} & {{I}_{z}} \\ \end{array} \right]\left[ \begin{matrix} {{\omega }_{xb}} \\ {{\omega }_{yb}} \\ {{\omega }_{zb}} \\ \end{matrix} \right]\text{=}\left[ \begin{matrix} {{M}_{xb}} \\ {{M}_{yb}} \\ {{M}_{zb}} \\ \end{matrix} \right] \\ \end{align}$ | (4) |
In the spacecraft attitude control system, attitude quaternion and angular velocity of spacecrafts are the output of the control system, and the torque of actuator is the input of the control system. It should be noted that the four components of quaternion are not independent. Therefore, only three of them need to be controlled. Letting x1 = [q1, q2, q3]T, x2 = [ωxb, ωyb, ωzb]T, u =[Mxb, Myb, Mzb]T, Eqs.(2) and (4) can be rewritten as follows respectively:
| ${{{\dot{x}}}_{1}}\text{=}{{f}_{1}}{{x}_{1}},\text{ }{{x}_{2}}=\frac{1}{2}\left[ \begin{array}{*{35}{l}} {{\omega }_{xb}} & 0 & {{\omega }_{zb}} & -{{\omega }_{yb}} \\ {{\omega }_{yb}} & -{{\omega }_{zb}} & 0 & {{\omega }_{xb}} \\ {{\omega }_{zb}} & {{\omega }_{yb}} & -{{\omega }_{xb}} & 0 \\ \end{array} \right]\left[ \begin{matrix} {{q}_{1}} \\ {{q}_{2}} \\ {{q}_{3}} \\ \end{matrix} \right]$ | (5) |
| $\begin{align} & {{{\dot{x}}}_{2}}={{f}_{2}}{{x}_{2}},\text{ }u={{\left[ \begin{array}{*{35}{l}} {{I}_{x}} & -{{I}_{xy}} & -{{I}_{xz}} \\ -{{I}_{yz}} & ~{{I}_{y}} & -{{I}_{yz}} \\ -{{I}_{zx}} & -{{I}_{zy}} & {{I}_{z}} \\ \end{array} \right]}^{-1}}\text{.} \\ & \left( -\left[ \begin{array}{*{35}{l}} 0 & {{\omega }_{zb}} & {{\omega }_{yb}} \\ {{\omega }_{zb}} & 0 & -{{\omega }_{xb}} \\ {{\omega }_{yb}} & {{\omega }_{xb}} & 0 \\ \end{array} \right]+\left[ \begin{array}{*{35}{l}} {{I}_{x}} & -{{I}_{xy}} & -{{I}_{xz}} \\ -{{I}_{yz}} & {{I}_{y}} & -{{I}_{yz}} \\ -{{I}_{zx}} & -{{I}_{zy}} & {{I}_{z}} \\ \end{array} \right].\left[ \begin{matrix} {{\omega }_{xb}} \\ {{\omega }_{yb}} \\ {{\omega }_{zb}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{M}_{xb}} \\ {{M}_{yb}} \\ {{M}_{zb}} \\ \end{matrix} \right] \right) \\ \end{align}$ | (6) |
+Letting y=[x1T, x2T]T and combining Eqs.(5) and (6) , yields
| $\dot{y}t=\left[ \begin{matrix} {{{\dot{x}}}_{1}}\left( t \right) \\ {{{\dot{x}}}_{2}}\left( t \right) \\ \end{matrix} \right]=\left[ \begin{matrix} {{f}_{1}}{{x}_{1}}\left( t \right),\text{ }{{x}_{2}}\left( t \right) \\ {{f}_{2}}{{x}_{2}}\left( t \right),\text{ }u\left( t \right) \\ \end{matrix} \right]$ | (7) |
Since MFAC is a control method for discrete-time systems, first order difference at time k is used to discretize the system dynamics model:
| $\dot{y}\left( k \right)\approx y\left( k+1 \right)-y\left( k \right)$ | (8) |
Substituting Eq.(7) into Eq.(8) , yields the discrete system state equation:
| $y\left( k+1 \right)=y\left( k \right)+\dot{y}\left( k \right)=\left[ \begin{array}{*{35}{l}} {{x}_{1}}\left( k \right)+{{f}_{1}}\left( {{x}_{1}}\left( k \right),\text{ }{{x}_{2}}\left( k \right) \right) \\ {{x}_{2}}\left( k \right)+{{f}_{2}}\left( {{x}_{2}}\left( k \right),\text{ }u\left( k \right) \right) \\ \end{array} \right]$ | (9) |
It is important to emphasize that the system model given in this paper will only be used to generate simulation data and have no effect on the designing of the controller. MFAC method only needs the input and output data of the system, and the designing of the controller is independent of the dynamic system model. In other word, the system output is a function of the system input, but the expression of the function is not needed.
3 Model-Free Adaptive Control MethodIt is a typical MIMO nonlinear discrete-time system with 3D input and 6D output presented in Eq.(9) . In order to keep input and output in the same dimension, a dimension reduction matrix C is introduced as
| $C=\left[ {{C}_{1}}{{C}_{2}} \right]\in {{R}^{3\times 6}}$ |
where C1, C2∈R3×3 are both the constant matrixes. The 6D output y turns into 3D output
| $\begin{array}{*{35}{l}} \tilde{y}\left( k+1 \right)=Cy\left( \left( k+1 \right)-{{y}_{d}}\left( k+1 \right) \right)= \\ {{C}_{1}}\left( {{x}_{1}}\left( k \right)+{{f}_{1}}{{x}_{1}}\left( k \right),\text{ }{{x}_{2}}\left( k \right)-{{x}_{1d}}\left( k+1 \right) \right)+ \\ {{C}_{2}}\left( {{x}_{2}}\left( k \right)+{{f}_{2}}{{x}_{2}}\left( k \right),\text{ }u\left( k \right)-{{x}_{2d}}\left( k+1 \right) \right)= \\ f\left( {{x}_{1}}\left( k \right),\text{ }{{x}_{2}}\left( k \right),\text{ }u\left( k \right),\text{ }{{x}_{1d}}\left( k+1 \right),\text{ }{{x}_{2d}}\left( k+1 \right) \right) \\ \end{array}$ | (10) |
where yd=[x1dT, x2dT]T is the desired system output and xid is the desired system state, i=1, 2. Eq.(10) is the augmented system model with 3D input and 3D output.
According to Eq.(10) , if
| $y\left( k+1 \right)\to {{y}_{d}}\left( k+1 \right)$ |
In other words, controlling the output
The output increment of system is defined as[17-21]
| ${{H}_{{{L}_{y}},\text{ }{{L}_{u}}}}k=\left[ \begin{array}{*{35}{l}} \tilde{y}\left( k \right) \\ \vdots \\ \tilde{y}\left( k-{{L}_{y}}+1 \right) \\ u\left( k \right) \\ \vdots \\ u\left( k-{{L}_{u}}+1 \right) \\ \end{array} \right]$ | (11) |
where the positive constants Ly and Lu are the system pseudo order.
Here are the hypotheses of system (10) :
Hypothesis 1 f holds continuous partial derivatives for all the variables.
Hypothesis 2 The system described in Eq.(10) meets the generalized Lipchitz condition, which means for arbitrary k1 ≠ k2,k1, k2 ≥ 0 and HLy, Lu( k1) ≠HLy, Lu( k2), there must be
| $\|\tilde{y}\left( {{k}_{1}}+1 \right)-y\tilde{\ }\left( {{k}_{2}}+1 \right)\|\le b\|{{H}_{{{L}_{y}},\text{ }{{L}_{u}}}}{{k}_{1}}-{{H}_{{{L}_{y}},\text{ }{{L}_{u}}}}\left( {{k}_{2}} \right)\|$ | (12) |
where b is a positive constant.
Let ΔHLy, Lu(k)=HLy, Lu(k)-HLy, Lu(k-1), Ly≥0, Lu≥1. If system (10) meets all the above hypotheses, when ‖ΔHLy, Lu(k)‖≠0, there must be a time-varying matrix, which is called pseudo partitioned Jacobian matrix (PPJM), so that system (10) can turn into full form dynamic linearization (FFDL) model[8]:
| $\Delta \tilde{y}\left( k+1 \right)={{\Phi }_{f,\text{ }{{L}_{y}},\text{ }{{L}_{u}}}}k\Delta {{H}_{{{L}_{y}},\text{ }{{L}_{u}}}}\left( k \right)$ | (13) |
and Φf, Ly, Lu(k)=[Φ1k, …ΦLy+Lu(k)] is bounded at any time k, where Φi(k)∈R3×3, i=1, …, Ly+Lu.
The control input criterion function is considered as
| $J\left( u\left( k \right) \right)=\|\tilde{y}\left( k+1 \right){{\|}^{2}}+\lambda \|u\left( k \right)-u\left( k-1 \right){{\|}^{2}}$ | (14) |
where λ is the weight coefficient.
Substituting Eq.(11) into Eq.(12) and letting the partial derivative of u(k) be equal to zero, yields
| $\begin{align} & \frac{\partial J}{\partial \left( u\left( k \right) \right)}={{\Phi }_{f,\text{ }{{L}_{y}}+1}}\left( k \right)[\tilde{y}k-{{\Phi }_{f,\text{ }{{L}_{y}}+1}}\left( k \right)\Delta uk- \\ & \sum\limits_{i=1}^{{{L}_{y}}}{{{\Phi }_{f,\text{ }i}}\left( k \right)\Delta \tilde{y}\left( k-i+1 \right)-} \\ & \sum\limits_{i=1}^{{{L}_{y}}+{{L}_{u}}}{{{\Phi }_{f,\text{ }i}}\left( k \right)\Delta u\left( k-i+{{L}_{y}}+1 \right)]-} \\ & \lambda \left( u\left( k \right) \right)-u\left( k-1 \right)=0 \\ \end{align}$ | (15) |
The solution of Eq.(15) is
| $\begin{align} & u\left( k \right)=u\left( k-1 \right)+\lambda {{(I+\Phi _{Ly+1}^{T}k{{\Phi }_{{{L}_{y}}+1}}\left( k \right))}^{-1}} \\ & \Phi _{Ly+1}^{T}\left( k \right)[{{\rho }_{{{L}_{y}}+1}}\tilde{y}\left( k \right)-\sum\limits_{i=1}^{{{L}_{y}}}{{{\rho }_{i}}}{{\Phi }_{i}}\left( k \right)\Delta y\left( k-i+1 \right)- \\ & \sum\limits_{i={{L}_{y}}+2}^{{{L}_{y}}+{{L}_{u}}}{{{\rho }_{i}}}{{\Phi }_{i}}\left( k \right)\Delta u\left( k-i+{{L}_{y}}+1 \right)] \\ \end{align}$ | (16) |
where ρi∈[0, 1], i=1, 2, …, Ly+Lu are the step size coefficients.
The calculation of Eq.(16) may be time-consuming with a high matrix dimension because of the matrix inversion, which is not beneficial for practical application. Therefore, Eq.(16) can be simplified as follows:
| $\begin{align} & u\left( k \right)=u\left( k-1 \right)+\frac{1}{\lambda +\|{{\Phi }_{{{L}_{y}}+1}}k{{\|}^{2}}}\cdot \\ & \Phi _{Ly+1}^{T}\left( k \right)[{{\rho }_{{{L}_{y}}+1}}\tilde{y}\left( k \right)-\sum\limits_{i=1}^{{{L}_{y}}}{{{\rho }_{i}}}{{\Phi }_{i}}\left( k \right)\Delta \tilde{y}(k- \\ & i+1)\text{ }-\sum\limits_{i={{L}_{y}}+2}^{{{L}_{y}}+{{L}_{u}}}{{{\rho }_{i}}}{{\Phi }_{i}}\left( k \right)\Delta u\left( k-i+{{L}_{y}}+1 \right)] \\ \end{align}$ | (17) |
It is noted that only Φf, Ly, Luk is unknown in Eq.(17) , which needs to be estimated on-line. The estimation criterion function is considered as
| $\begin{align} & J\left( {{\Phi }_{f,\text{ }{{L}_{y}},\text{ }{{L}_{u}}}}\left( k \right) \right)=\|\Delta \tilde{y}\left( k \right)-{{\Phi }_{f,\text{ }{{L}_{y}},\text{ }{{L}_{u}}}}\left( k \right)\Delta {{H}_{{{L}_{y}},\text{ }{{L}_{u}}}}\left( k-1 \right)\|{{)}^{2}}+ \\ & \begin{array}{*{35}{l}} \mu \|{{\Phi }_{f,\text{ }{{L}_{y}},\text{ }{{L}_{u}}}}\left( k \right)-{{{\hat{\Phi }}}_{f,\text{ }{{L}_{y}},\text{ }{{L}_{u}}}}\left( k-1 \right)\|{{)}^{2}} \\ {} \\ \end{array} \\ \end{align}$ | (18) |
where μ is the weight coefficient, and
| $\begin{align} & {{{\hat{\Phi }}}_{f,Ly,Lu}}\left( k \right)={{{\hat{\Phi }}}_{f,Ly,Lu}}\left( k-1 \right)+ \\ & \frac{\eta (\Delta \tilde{y}~\left( k \right)-{{{\hat{\Phi }}}_{f,Ly,Lu}}\left( k-1 \right)\Delta H_{Ly,Lu}^{T}\left( k-1 \right)}{\mu +\left\| \Delta {{H}_{Ly,Lu}} \right\|} \\ \end{align}$ | (19) |
where η is the step size coefficient.
The main steps of MFAC scheme are summarized as follows:
1) Initialization;
2) Measure (or simulate)_ input and output of system;
3) Calculate ΔHLy, Lu(k-1) using Eq.(11) ;
4) Estimate
5) Calculate u(k) using Eq.(16) ;
6) Return to Step 2 until finish.
4 Numerical SimulationThe verification of MFAC for the attitude control of the single rigid spacecraft is presented in this section. When spacecraft is conducting an on-orbit operation, the inertia matrix of the spacecraft will change over time and cannot be acquired accurately because of the relative movement of the system components. Therefore, it is difficult to deal with such problems for traditional model-based control methods.
Case A. Same Controller Parameters for Different Models.
Numerical simulation of MFAC is conducted by using different dynamic model parameters. Controller parameters are shown in Table 1. It should be noted that the system dynamic model is only used to generate the input and output data in the numerical simulation, which is not related to the designing of the controller. The desired system states are x1d = [0,0,0]T rad and x2d=[0,0,0]T rad/s. The simulation time is tf=300 s. The initial value of system is shown in Table 2.
| $1)\text{ }I={{I}_{1}}=\left[ \begin{array}{*{35}{l}} 100 & 0 & 0 \\ 0 & 120 & 0 \\ 0 & 0 & 150 \\ \end{array} \right]$ |
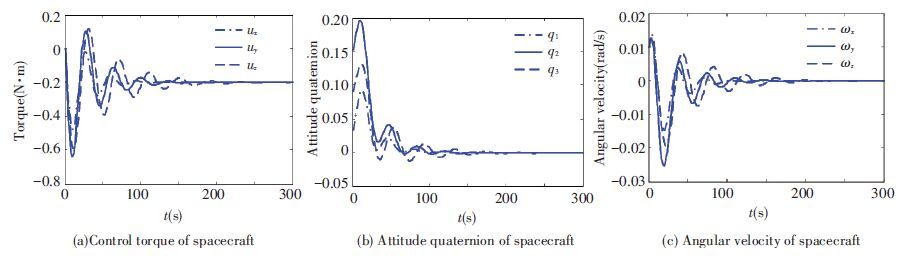
The simulation results are shown in Fig. 1. All system states (including attitude quaternion and attitude angular velocity) converge to zero, which proves the validity of the algorithm.
| Table 1 Parameters of controller |
| Table 2 Initial value of system |
|
Figure 1 MFAC for I=I1 |
| $2)\text{ }I={{I}_{2}}=\left[ \begin{array}{*{35}{r}} 10 & 0 & 0 \\ 0 & 12 & 0 \\ 0 & 0 & 15 \\ \end{array} \right]$ |
The simulation results are shown in Fig. 2. Compared Fig. 1 with Fig. 2, the system states of both situations converge to zero with the same controller parameters. There is no need to alter controller parameters though the controlled systems are different, which means the design of the controller presented in this paper does not rely on system model. On the other hand, from Fig. 2, the control input u reduces to a very small value rapidly while the system states have not converged to zero at that time. It is supposed that the output is related with the previous inputs and outputs in FFDL model adopted in MFAC algorithm. As a result, the previous outputs can be used to control the system states despite of the small control input. Its physical essence is to control the attitude angle by angular velocity of the spacecraft, which matches with our practical experience. However, the convergence speed of MFAC may be slower than that of model based control method if the controlled system model is fully known.
Case B. Controller Performance for Time-varying System, Compared with PD Control.
In order to compare the performance of MFAC with PD control, it is supposed that the inertia matrix of spacecraft is time-varying as follows:
| $It=\frac{{{I}_{f}}-{{I}_{0}}}{{{t}_{f}}}t+{{I}_{0}}~~$ |
where I0 and If are the inertia matrixes at initial time and final time, respectively, which can be chosen as I0= I1,If=I2. The constant disturbing torque Td=[0.2, 0.2, 0.2]T N·m is taken into account.
PD Control law can be given as
| $u\left( k \right)={{K}_{P}}{{x}_{1}}\left( k \right)+{{K}_{D}}{{x}_{2}}\left( k \right)$ |
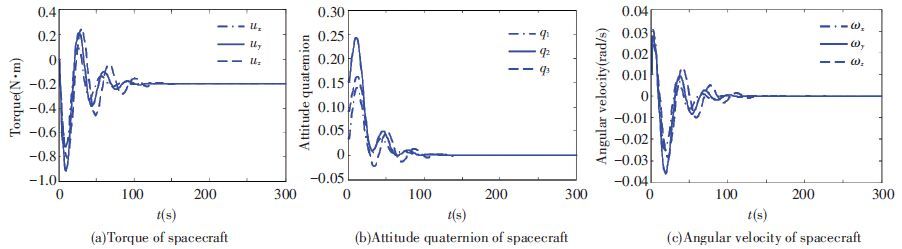
where KP=10 and KD=16. The simulation result is presented in Fig. 3 with the inertial value in Table 2. Although the system states can converge to zero in PD control, the attitude quaternion remains steady state error. The simulation result using MFAC is shown in Fig. 4 with the same controller parameters in Table 1 and the inertial value in Table 2. The spacecraft attitude quaternion and attitude angular velocity tend to be stable and converge to zero without steady state error though the inertia matrix of the spacecraft keep changing constantly and the disturbing torque exists in the dynamic model. The controller performance of MFAC is superior to that of PD Control.

|
Figure 2 MFAC for I=I2 |

|
Figure 3 PD control for time-varying system with disturbing torque |
|
Figure 4 MFAC for time-varying system with disturbing torque |
5 Conclusions
In order to use MFAC in spacecraft attitude control system effectively, a dimension reduction matrix is introduced to construct an augmented system with the same dimension input and output. Based on this method, an improved spacecraft attitude MFAC algorithm is proposed. The numerical simulation results show that the same set of MFAC controller parameters can be used in different spacecraft models. MFAC can be also used for the system with time-varying parameters and disturbing torque. The simulation results show that MFAC has better controller performance than PD control. Besides, MFAC is suitable for any general second-order dynamical system like spacecraft attitude control system.
| [1] |
Lai Aifang, Guo Yu, Zheng Lijun. Active disturbance rejection control for spacecraft attitude maneuver and stability.
Control Theory & Applications, 2012 , 29 (3) : 401-407.
( 0) 0)
|
| [2] |
Wu Zhong, Huang Liya, Wei Kongming, et al. Active disturbance rejection control of attitude for spacecraft.
Control Theory & Applications, 2013 , 30 (12) : 1617-1622.
( 0) 0)
|
| [3] |
Jin Yongqiang, Liu Xiangdong, Qiu Wei, et al. Time-varying sliding mode controls in rigid spacecraft attitude tracking.
Chinese Journal of Aeronautics, 2008 , 21 (4) : 352-360.
DOI:10.1016/S1000-9361(08)60046-1 ( 0) 0)
|
| [4] |
Cong Binglong, Liu Xiangdong, Chen Zhen. An improved adaptive sliding mode control for spacecraft attitude control.
Control and Decision, 2012 , 27 (10) : 1471-1476.
( 0) 0)
|
| [5] |
Zhang Jingrui, Zhang Weitai, Zeng Xiangyuan, et al. Robust controller design for the attitude control of spacecraft with uncertainty.
Transactions of Beijing Institute of Technology, 2011 , 31 (10) : 1198-1202.
( 0) 0)
|
| [6] |
Wang Biao, Tang Chaoying. Adaptive neural-network-based inverse method and its application in spacecraft attitude control.
Systems Engineering and Electronics, 2007 , 29 (2) : 246-249.
( 0) 0)
|
| [7] |
Wei Fengmei, Zhao Yushan, Shi Peng. Variable universe self-tuning fuzzy PID controller of attitude maneuver for flexible spacecraft.
Chinese Space Science and Technology, 2014 , 6 : 1-7.
( 0) 0)
|
| [8] |
Hou Zhongsheng.
Nonparametric Models and Its Adaptive Control Theory. Beijing: Science Press, 1999 : 102 -115.
( 0) 0)
|
| [9] |
Wang Xiaoming, Xu Tianpeng. Water level control of boiler stream drum based on MFAC-PID.
Journal of Central South University (Science and Technology), 2013 , 44 : 52-57.
( 0) 0)
|
| [10] |
Wang Junwei, Zhang Guoding. Model-free adaptive technology for pH control of neutralization step in manufacture process of fatty acidmethylester sulfonat.
China Surfactant Detergent & Cosmetic, 2008 , 38 (2) : 132-136.
( 0) 0)
|
| [11] |
Zhao Yi, Lu Chao, Han Yingduo, et al. Wide area power system stablilizer design based on improved model free adaptive control.
Journal Tsinghua University (Science and Technology), 2013 , 53 (11) : 1645-1652.
( 0) 0)
|
| [12] |
Lv Fenglin, Chen Huabin, Fan Chongjian, et al. Application of model-free adaptive control to impulse TIG welding.
Journal of Shanghai Jiaotong University, 2009 , 43 (1) : 61-70.
( 0) 0)
|
| [13] |
Wang Yuegang, Zuo Zhaoyang, Guo Zhibin, et al. Application of slide mode/model-free method in centrifuge-vibration test system.
Journal of Chinese Inertial Technology, 2014 , 22 (2) : 276-280.
( 0) 0)
|
| [14] |
Hou Zhongsheng, Dong Hangrui, Jin Shang Tai. Model-free adaptive control with coordinates compensation for automatic car parking systems.
Acta Automatica Sinica, 2015 , 4 : 823-831.
( 0) 0)
|
| [15] |
Guo Haifeng, Cheng Jun, Fang Liangjun, et al. Model-free adaptive control method for isolated intersection based on short-term prediction.
China Journal of Highway and Transport, 2014 , 12 : 88-95.
( 0) 0)
|
| [16] |
Ma Jie, Chen Zhiyong, Hou Zhongsheng. Model-free adaptive control of integrated roll-reducing system for large warships.
Control Theory & Applications, 2009 , 11 : 1289-1292.
( 0) 0)
|
| [17] |
Hou Zhongsheng. On model-free adaptive control: the state of the art and perspective.
Control Theory & Applications, 2006 , 4 : 586-592.
( 0) 0)
|
| [18] |
Zhu Yuanming, Hou Zhongsheng. Data-driven MFAC for a class of discrete-time nonlinear systems with RBFNN.
IEEE Transactions on Neural Networks and Learning Systems, 2014 , 25 (5) : 1013-1020.
DOI:10.1109/TNNLS.2013.2291792 ( 0) 0)
|
| [19] |
Zhu Yuanming, Hou Zhongsheng. Controller-dynamic-linearization-based model free adaptive control for discrete-time nonlinear systems.
IEEE Transactions on Industrial Informatics, 2013 , 9 (4) : 2301-2309.
DOI:10.1109/TII.2013.2257806 ( 0) 0)
|
| [20] |
Hou Zhongsheng, Jin Shangtai. A novel data-driven control approach for a cass of discrete-time nonlinear systems.
IEEE Transactions on Control Systems Technology, 2011 , 19 (6) : 1549-1558.
DOI:10.1109/TCST.2010.209313 ( 0) 0)
|
| [21] |
Javadi A, Pezeshki S. A new model-free adaptive controller versus non-linear H∞ controller for levitation of an electromagnetic system.
Transactions of the Institute of Measurement and Control, 2013 , 35 : 321-329.
DOI:10.1177/0142331212444664 ( 0) 0)
|
 2016, Vol. 23
2016, Vol. 23

