2. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China;
3. Key Laboratory of Road and Traffic Engineering, Ministry of Education, Shanghai 201804, China
So far, many models, such as the cellular automaton (CA) models and the car-following models, have been applied to analyze the complex traffic phenomena. These models are used to describe the micro characteristics of car motion and explore the microscopic traffic flow phenomena. The car-following models show the microscopic characteristics of traffic flow by using the interaction between front and rear cars. Herman and Chandler et al. proposed the linear models[1]. Subsequently, Gazis et al. proposed the nonlinear models[2]. Based on the above models, remarkable improvements were achieved[3-7]. One can deduce from Ref.[3] that Bando and others proposed OV (Optimal Velocity) model according to traffic analysis in 1995 which was then widely applied[4]. And many scholars proposed a series of OV extended models, which considered many cars' relative position or the relative speed of the near vehicle, to enhance the stability of the traffic flow.
Most of the existing car-following models focus on the normal traffic condition[8-12]. In fact, under ice and snowfall conditions, the visibility and friction factor decline significantly, and the traffic property and drivers' behaviors are crucially distinct from those under the normal state. Drivers will keep bigger headway and space headway, and make slighter acceleration or deceleration under ice and snowfall conditions. As a result, the car-following model is not the same as the normal one. However, there are very few car-following models which focus on ice and snowfall conditions. Hence, in this paper, we directly focus on car-following model to describe the characteristics of car motion under ice and snowfall conditions, then grasp the stability conditions of traffic flow by linear analysis, and finally verify the rationality of the proposed model by nonlinear analysis and numerical simulation.
2 Model EstablishmentBandoet al.[3] proposed this model:
| $ \frac{{{\rm{d}}{v_n}}}{{{\rm{d}}t}} = {a_1}\left[ {V\left( {\Delta {x_n}} \right) - {v_n}} \right] $ | (1) |
where, a1 is the sensitivity coefficient to the vehicle in front, Δxn=xn+1-xn, is the space headway, xn and xn+1 are the locations of the flowing car and the first car respectively, vn is the velocity of the following car, and V (Δxn) is the optimal velocity.
According to the observed data, Helbing and Tilch identified the parameters of OV model[13]. It turns out that there are excessive acceleration and deceleration issues among OV model. Therefore they proposed the following GF (General Force) model:
| $ \frac{{{\rm{d}}{v_n}}}{{{\rm{d}}t}} = {a_1}\left[ {V\left( {\Delta {x_n}} \right) - {v_n}} \right] + {\lambda _1}\Delta {v_n}H\left( { - \Delta {v_n}} \right) $ | (2) |
where, Δvn=vn+1-vn is the relative velocity, H(-Δvn) is the Heaviside function, and λ1 is the reaction coefficient of the relative velocity to the vehicle in front.
In the real traffic flow, when the current car is much faster than the following one, the following car will not slow down although the space headway is shorter than the safe distance. Neither the OV model nor the GF model can explain this phenomenon, so Jiang et al.[7] proposed the FVD (Full Velocity Difference) model:
| $ \frac{{{\rm{d}}{v_n}}}{{{\rm{d}}t}} = {a_1}\left[ {V\left( {\Delta {x_n}} \right) - {v_n}} \right] + {\lambda _1}\Delta {v_n} $ | (3) |
All the above models are proposed based on a construction of normal road traffic conditions. However, the visibility and friction factor decline significantly under ice and snowfall conditions, where drivers will keep bigger headway and space headway as well as make slighter acceleration and deceleration. Therefore, considering the impact of ice and snowfall conditions on car-following behavior, this paper proposes the car-following model under ice and snowfall conditions based on Jiang's model[7].
| $ {{x''}_n}\left( t \right) = a\left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right] + {\mu _0}\left( {{f_r}/f_r^0} \right)\Delta {v_n} $ | (4) |
where, μ0 represents the reaction coefficient of the relative velocity of the vehicle in front and the road surface friction coefficient under ice and snowfall conditions, it may be gotten by field observation; fr0 is the road surface friction coefficient under normal traffic condition; fr is the road surface friction coefficient under ice and snowfall conditions. fr0 and fr may be gotten by field observation, under very smooth ice film fr=0.1, very smooth compacted snow fr=0.15, ice sheet fr=0.175, ice film fr=0.225, ice sheet under snow fr=0.25, mild compacted snow fr=0.3 as well as fr0=0.6.
3 Linear Stability AnalysisIn this section, according to Refs.[7, 14], we study the linear stability of the model established in this paper. Setting λ=μ0(fr/fr0), assuming that the initial state is steady. The space headway is b. The corresponding speed is V(b). Now the solution of vehicle location of the steady traffic flow is:
| $ x_n^0\left( t \right) = bn + V\left( b \right)t $ | (5) |
For uniform flow solution (5), plus a perturbation yn(t), we get:
| $ \begin{array}{l} {x_n}\left( t \right) = x_n^0\left( t \right) + {y_n}\left( t \right)\\ {y_n}\left( t \right) = {x_n}\left( t \right) - x_n^0\left( t \right) \end{array} $ | (6) |
Seeking the first and the second derivatives, we get:
| $\begin{array}{l} y{'_n}\left( t \right) = x{'_n}\left( t \right) - x{'_n}^0\left( t \right)\\ \;\;\;\;\;y'{'_n}\left( t \right) = x'{'_n}\left( t \right) \end{array}$ |
where
Then
| $ \begin{array}{*{20}{c}} {\Delta {x_n} = {x_{n + 1}} - {x_n} = b + {y_{n + 1}} - {y_n} = b + \Delta {y_n}}\\ {\Delta {v_n} = {{x'}_{n + 1}} - {{x'}_n} = {{y'}_{n + 1}} - {{y'}_n} = \Delta {{y'}_n}} \end{array} $ |
Substituting the above equations into Eq.(1), linearizing the equation and getting:
| $ \begin{array}{l} {{y''}_n} = a\left[ {V\left( {\Delta {x_n}} \right) - {v_n}} \right] + f\Delta {v_n} = a\left[ {V\left( {b + \Delta {y_n}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {v\left( b \right) - {{y'}_n}} \right] + f\Delta {v_n} \end{array} $ | (7) |
Setting yn(t)=e(zt+αni), by Fourier series expansion for yn(t), and the results substituted into Eq.(7), and then we can get:
| $ {z^2} + z\left[ {a - f\left( {{{\rm{e}}^{{a_k}{\rm{i}}}} - 1} \right)} \right] - aV'\left( b \right)\left( {{{\rm{e}}^{{a_k}{\rm{i}}}} - 1} \right) = 0 $ | (8) |
Setting z=ωi, eaki=cos αk+isin αk, we get:
| $ \begin{array}{l} - {\omega ^2} + wi\left[ {a - f\left( {\cos {\alpha _k} - 1 + {\rm{isin}}{\alpha _k}} \right)} \right] - \\ \;\;aV'\left( b \right)\left( {\cos {\alpha _k} - 1 + {\rm{isin}}{\alpha _k}} \right) = 0 \end{array} $ | (9) |
Making the real and the imaginary part zero, we get:
| $ \begin{array}{l} V'\left( b \right) = {\left\{ {\left( {1 - \cos {\alpha _k}} \right)\left[ {a + f\left( {1 - \cos {\alpha _k}} \right)} \right]} \right.^2} + \\ \left. {\;\;\;\;\;\;\;\;\;\;\;f{{\sin }^2}{\alpha _k}\left[ {a + f\left( {1 - \cos {\alpha _k}} \right)} \right]} \right\}/a{\sin ^2}{\alpha _k} \end{array} $ | (10) |
When ak→0, apply the L'Hospital law to obtain the critical stable curve:
| $ V'\left( b \right) = \lambda + \frac{a}{2} = {\mu _0}\left( {{f_r}/f_r^0} \right) + \frac{a}{2} $ |
When the space headway satisfies the following relationship, the system will be in a steady state
| $ V'\left( b \right) < {\mu _0}\left( {{f_r}/f_r^0} \right) + \frac{a}{2} $ | (11) |
When fr/fr0=1, Eq.(11) is consistent with the model stability in Refs.[7, 14]. Meeting Eq.(11), the disturbance is small, the traffic flow will be stable; on the contrary, the traffic flow will be unstable. With the introduction of road surface friction coefficient in the model, the stability of traffic flow under different road conditions can be explored.
Parameter fr is the road surface friction coefficient under ice and snowfall conditions. It may be gotten by field observation, under very smooth ice film fr=0.1, very smooth compacted snow fr=0.15, ice sheet fr=0.175, ice film fr=0.225, ice sheet under snow fr=0.25 as well as mild compacted snow fr=0.3. The simulation rendering critical stable curves under the seven different road conditions are shown in Fig. 1, where the region above the curve is stable, otherwise it is unstable. It shows that when road conditions become harsher, especially the friction coefficient becomes smaller, the stable area of traffic flow gets much smaller.
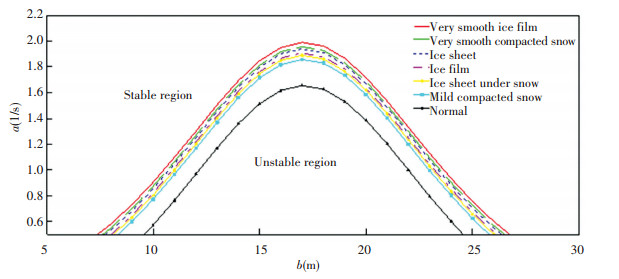
|
Figure 1 Critical stable curve under different road conditions |
4 Nonlinear Analysis
In this section, with Refs.[7, 14-15], we study the nonlinear analysis of the model established in this paper. When traffic flow is in the unstable region or near the critical point, the slow variables will change. Density wave is the form of kink-anti-kink solitary wave[15]. To refer to Ref.[15] for more details. When m=1, the model is equivalent to this paper's situation.
| $ {{x''}_n}\left( t \right) = a\left[ {V\left( {\Delta {x_n}\left( t \right)} \right) - {v_n}\left( t \right)} \right] + \lambda \Delta {v_n} $ | (12) |
Using perturbation method kinetic for nonlinear analysis to obtain kink-anti-kink solitary wave solutions. Eq.(12) can be rewritten as:
| $ \begin{array}{l} \frac{{{{\rm{d}}^2}\left( {\Delta {x_n}\left( t \right)} \right)}}{{{\rm{d}}t}} = a\left[ {V\left( {\Delta {x_{n + 1}}\left( t \right)} \right) - V\left( {\Delta {x_n}\left( t \right)} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\frac{{{\rm{d}}\Delta {x_n}}}{{{\rm{d}}t}}} \right] + \lambda \left( {\frac{{{\rm{d}}\left( {\Delta {x_n} - 1} \right)}}{{{\rm{d}}t}} - \frac{{{\rm{d}}\left( {\Delta {x_n}} \right)}}{{{\rm{d}}t}}} \right) \end{array} $ | (13) |
Considering changes in the slow variable behavior near the critical point, a=ac,
And defining the variables X, T:
| $ \begin{array}{l} X = \varepsilon \left( {N + bt} \right)\\ \;\;\;\;\;\;\;T = {\varepsilon ^3}t \end{array} $ |
where b is the unknown parameter.
Making space headway as Δxn(t)=hc+εR(X, T).
Eq.(13) expands to ε5 order, and then the nonlinear partial differential equation is obtained as follows.
| $ \begin{array}{l} {\varepsilon ^2}\left( {b - V'} \right){\partial _X}R + {\varepsilon ^3}\left( {\frac{{{b^2}}}{a} - \frac{{V'}}{2} - \lambda \frac{b}{a}} \right)\partial _X^2R + \\ \;\;\;\;{\varepsilon ^4}\left[ {\partial _T^2R + \left( { - \frac{{V'}}{6} - \lambda \frac{b}{{2a}}} \right)\partial _X^3R - \frac{{V'''}}{6}\partial _X^3{R^3}} \right] + \\ \;\;\;\;{\varepsilon ^5}\left[ {\left( {\frac{{2b}}{a} - \frac{\lambda }{a}} \right){\partial _T}{\partial _X}R + \left( { - \frac{{V'}}{{24}} - \frac{{\lambda b}}{{24a}}} \right)} \right.\partial _X^4R - \\ \;\;\;\;\;\left. {\frac{{V'''}}{{12}}\partial _X^2{R^3}} \right] = 0 \end{array} $ | (14) |
where
| $ V' = \frac{{{\rm{d}}\mathit{V}\left( {\Delta x} \right)}}{{{\rm{d}}\Delta x}}\left| {_{\Delta x = {h_c}}} \right.,V''' = \frac{{{{\rm{d}}^3}\mathit{V}\left( {\Delta x} \right)}}{{{\rm{d}}\Delta {x^3}}}\left| {_{\Delta x = {h_c}}} \right. $ |
Taking b=V′,
| $ \begin{array}{l} {\varepsilon ^4}\left[ {{\partial _T}R + {g_1}V'\partial _X^3R + {g_2}{\partial _X}{R^3}} \right] + {\varepsilon ^5}\left[ {{g_3}\partial _X^2R + } \right.\\ \;\;\;\;\;\;\left. {{g_4}\partial _X^2{R^3} - {g_5}\partial _X^4R} \right] = 0 \end{array} $ | (15) |
where
| $ \begin{array}{*{20}{c}} {{g_1} = \frac{{V'}}{6} + \frac{1}{2}\frac{{\lambda V'}}{{{a_c}}},{g_2} = - \frac{{V'''}}{6},{g_3} = \frac{{V'}}{2},}\\ {{g_4} = \left( {\frac{{2V'}}{{{a_c}}} - \frac{\lambda }{{{a_c}}}} \right)\left( {\frac{{V'}}{6} + \frac{1}{2}\frac{{\lambda V'}}{{{a_c}}}} \right) + \left( { - \frac{{V'}}{{24}} + \frac{1}{6}\frac{{\lambda V'}}{{{a_c}}}} \right)}\\ {{g_5} = - \frac{{V'}}{{12}}\left( {1 - \frac{{4V'}}{{{a_c}}} - 2\lambda } \right)} \end{array} $ |
Making the following transformation to Eq.(15), setting T′=g1V′T,
| $ {\partial _T}R' - \partial _X^3R' + {\partial _X}{{R'}^3} + \varepsilon M\left[ {R'} \right] = 0 $ | (16) |
| $ M\left[ {R'} \right] = \sqrt {\frac{1}{{{g_1}}}} \left[ {{g_3}\partial _X^2R' + \frac{{{g_1}{g_5}}}{{{g_2}}}\partial _X^2{{R'}^3} + {g_4}\partial _X^4R'} \right] $ | (17) |
Omitted o(ε) item, the kink-anti-kink wave solution is:
| $ {{R'}_0}\left( {X,T'} \right) = \sqrt c \tanh \sqrt {c/2} \left( {X - cT'} \right) $ | (18) |
In order to obtain the propagation velocity c to Eq.(17), solvability condition must be met:
| $ \left( {{{R'}_0},M\left[ {{{R'}_0}} \right]} \right) = \int_{ - \infty }^{ + \infty } {{{R'}_0}\left( {X,T'} \right)M\left[ {{{R'}_0}\left( {X,T'} \right)} \right]{\rm{d}}X} = 0 $ | (19) |
By integrating, we can get the speed of kink-anti-kink wave propagation
| $ c = 5{g_2}{g_3}/\left( {2{g_2}{g_4} - 3{g_1}{g_5}} \right) $ |
so the solution to above equation is:
| $ \begin{array}{l} R\left( {X,T} \right) = \sqrt {\left( { - V' + \frac{{3\lambda V'}}{{{a_c}}}} \right)\left( {\frac{{{a_c}}}{a} - 1} \right)\frac{c}{{V'''}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tanh \sqrt {\frac{c}{2}} \left( {X - \frac{{cTV'}}{6} + \frac{{\lambda V'}}{{2{a_c}}}} \right) \end{array} $ | (20) |
so the solution to kink-anti-kink density wave of the space headway is:
| $ \begin{array}{l} \Delta {x_n}\left( t \right) = {h_c} + \sqrt {\left( { - V' + \frac{{3\lambda V'}}{{{a_c}}}} \right)\left( {\frac{{{a_c}}}{a} - 1} \right)\frac{c}{{V'''}}} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tanh \sqrt {\frac{c}{2}} \left( {X - \frac{{cTV'}}{6} + \frac{{\lambda V'}}{{2{a_c}}}} \right) \end{array} $ | (21) |
so the amplitude of the solution to kink-anti-kink density wave is:
| $ B = \sqrt {\left( { - V' + \frac{{3\lambda V'}}{{{a_c}}}} \right)\left( {\frac{{{a_c}}}{a} - 1} \right)\frac{c}{{V'''}}} $ |
Kink wave solutions stand for the coexisting phases. And the coexistence curve can be plotted by the following formula:
| $ \Delta {x_n}\left( t \right) = {h_c} \pm B $ | (22) |
To verify the application of the model proposed in this paper, a numerical simulation was conducted. In the simulation, the OV function proposed by Helbing et al. was adopted[8].
| $ V\left( {\Delta x} \right) = {v_1} + {v_2} + \tanh \left[ {{C_1}\left( {\Delta x - {l_c}} \right) - {C_2}} \right] $ | (23) |
where, lc is a car length, taking 5 m, v1=6.75 m/s, v2=71.91 m/s, C1=0.13 m-1, C2=1.57 m-1. In the periodic boundary conditions, take the loop length L=1 500 m, the number of vehicles N=100, the initial disturbance is:
| $ \begin{array}{*{20}{c}} {{x_1}\left( 0 \right) = 10{\rm{m}},{x_n}\left( 0 \right) = \left( {n - 1} \right)L/N,\left( {n = 2,3, \cdots ,N} \right)}\\ {{v_n}\left( 0 \right) = V\left( {L/N} \right)\left( {n = 1,2,3, \cdots ,N} \right)} \end{array} $ |
Taking a=1.85 s-1, μ0=0.2 s-1, from the critical stability curve we know all the models under various road conditions are stable. Where there is initial disturbance, taking t=100, 300, 1 000, 1 500 s, the numerical simulation of vehicle speed under different road conditions are shown in Fig. 2.

|
Figure 2 Velocity distribution |
From the simulation results in Fig. 2, it is found that the speed of vehicles under different road conditions fluctuates around the initial velocity v0=4.664 7 m/s with the initial disturbance for a long time. As time goes by, the speed of the vehicle will tend to be stable. At the same time, it is obvious that the harsher road conditions are, the larger vehicle speed volatility is, which indicates traffic flow more unstable. If the sensitivity coefficient takes a smaller value, the traffic flow under poor road conditions may lose its original stability, further causing traffic congestion. Therefore, the worse road condition is, the more sensitive to the model will be. This is consistent with previous results of linear stability analysis.
Taking a=1.5, t=1 500 s, the numerical simulation under different road conditions the phase space (space headway -the velocity space) hysteresis loop, as shown in Fig. 3. By the linear stability analysis, it shows, a=1.5 in this case, the road condition and traffic are not stable, thus in the process of evolution, vehicles will change from unimpeded to crowded, and then from crowded back to unimpeded. However, such a process is not the same as closing a reply. There is hysteresis. From Fig. 3, the worse road condition is, the larger the area formed by the phase space in the closed hysteresis loop will be (i.e. the greater the instability region). When the value of a is taken to meet the stability condition, only one dot exists in the phase space not forming a hysteresis loop. This is consistent with the previous results of nonlinear analysis.

|
Figure 3 Different models of hysteresis loop road conditions |
Numerical simulation under different road conditions at the same time (t=1 500 s) and different time (t=1 490 s and t=1 500 s) the same road conditions (in a very smooth ice film for example) all vehicles space headway distribution, as shown in Figs. 4, 5 and 6, respectively. Through the non-linear analysis, traffic flow in the unstable region, the critical point (hc, ac) density wave is kink-anti-kink solitary wave form. Figs. 4 and 5 illustrate that the amplitude of density waves increases along with the deterioration of road conditions, that is to say, traffic flow easily causes instability in poor road conditions, forming stop-go density waves. Fig. 6 shows that the waveforms in the unstable region at different moments are exactly the same. When density waves propagate upstream, the vehicles in front will decelerate and park, which may lead to queuing and congestion.
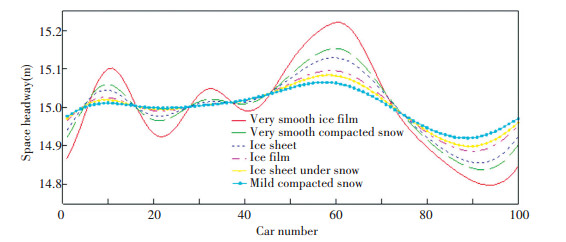
|
Figure 4 Distribution of space headway under different road conditions (a=1.85, t=1 500 s) |

|
Figure 5 Distribution of space headway under different road conditions (a=1.5, t=1 500 s) |

|
Figure 6 Distribution of space headway at different time (a=1.5, t=1 490 and 1 500 s) |
6 Conclusions
This paper proposes an improved car-following model considering the coefficient of road friction, based on the influence of different road conditions on propagation characteristics of traffic wave under ice and snowfall conditions. After the linear stability analysis, stability conditions of car following model under different road conditions are identified. In addition, critical stable curves under seven different road conditions are drawn. The results show that when road conditions become harsher, especially the friction coefficient diminishes, the stable area of traffic flow gets much smaller. Traffic congestion is the limiting form of density wave propagation caused by the interaction of the vehicles. It can be concluded from nonlinear analysis that density wave is in kink-anti-kink solitary wave form, considering variation behavior of the slow variables in the unstable region or near the critical point of traffic flow. Through deduction, kink-anti-kink density wave solutions of distance headway and coexistence curve are obtained. Numerical simulation results show that worse road conditions or greater speed fluctuations will lead to greater instability region of traffic flow and less absorption interference ability, even it can cause more congestion and accidents. Ultimately, the conclusions have great significance in solving the problems of traffic congestions and security under ice and snowfall conditions.
| [1] |
Herman R, Montroll E W, Potts R B, et al. Traffic dynamics: Analysis of stability in car following.
Operations Research, 1959, 7(1): 86-106.
DOI:10.1287/opre.7.1.86 ( 0) 0)
|
| [2] |
Gazis D C, Herman R, Rothery R W. Nonlinear follow-the-leader models of traffic flow.
Operations Research, 1961, 9(4): 545-567.
DOI:10.1287/opre.9.4.545 ( 0) 0)
|
| [3] |
Bando M, Hasebe K, Nakayama A, et al. Dynamical model of traffic congestion and numerical simulation.
Physical Review E, 1995, 51(2): 1035.
DOI:10.1103/PhysRevE.51.1035 ( 0) 0)
|
| [4] |
Chen D, Laval J, Zheng Z, et al. A behavioral car-following model that captures traffic oscillations.
Transportation Research Part B: Methodological, 2012, 46(6): 744-761.
DOI:10.1016/j.trb.2012.01.009 ( 0) 0)
|
| [5] |
Saifuzzaman M, Zheng Z, Haque M M, et al. Revisiting the task-capability interface model for incorporating human factors into car-following models.
Transportation Research Part B: Methodological, 2015, 82: 1-19.
( 0) 0)
|
| [6] |
Yu S, Shi Z. An improved car-following model considering relative velocity fluctuation.
Communications in Nonlinear Science and Numerical Simulation, 2016, 36: 319-326.
DOI:10.1016/j.cnsns.2015.11.011 ( 0) 0)
|
| [7] |
Jiang R, Wu Q, Zhu Z. Full velocity difference model for a car-following theory.
Physical Review E, 2001, 64(1): 017101.
DOI:10.1103/PhysRevE.64.017101 ( 0) 0)
|
| [8] |
Peng G, Lu W, He H, et al. Nonlinear analysis of a new car-following model accounting for the optimal velocity changes with memory.
Communications in Nonlinear Science and Numerical Simulation, 2016, 40: 197-205.
DOI:10.1016/j.cnsns.2016.04.024 ( 0) 0)
|
| [9] |
Jin Y, Xu M. Stability analysis in a car-following model with reaction-time delay and delayed feedback control.
Physica A: Statistical Mechanics and Its Applications, 2016, 459: 107-116.
DOI:10.1016/j.physa.2016.04.038 ( 0) 0)
|
| [10] |
Ge H, Meng X, Ma J, et al. An improved car-following model considering influence of other factors on traffic jam.
Physics Letters A, 2012, 377(1): 9-12.
( 0) 0)
|
| [11] |
Sun D, Kang Y, Yang S. A novel car following model considering average speed of preceding vehicles group.
Physica A: Statistical Mechanics and Its Applications, 2015, 436: 103-109.
DOI:10.1016/j.physa.2015.04.028 ( 0) 0)
|
| [12] |
Yu S, Shi Z. An extended car-following model at signalized intersections.
Physica A: Statistical Mechanics and Its Applications, 2014, 407: 152-159.
DOI:10.1016/j.physa.2014.03.081 ( 0) 0)
|
| [13] |
Helbing D, Tilch B. Generalized force model of traffic dynamics.
Physical Review E, 1998, 58(1): 133.
DOI:10.1103/PhysRevE.58.133 ( 0) 0)
|
| [14] |
Xue Y, Dong L Y, Yuan Y W, et al. Numerical simulation on traffic flow with the consideration of relative velocity.
Acta Physica Sinica, 2002, 51(3): 492-496.
( 0) 0)
|
| [15] |
Pang G H. Stabilization analyzing of multiple look-ahead car-following mode.
Systems Engineering-Theory & Practice, 2011, 3: 22.
( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


