Nowadays the complex networks have many applications in modern life, such as power grids, communications, epidemic spreads and so on. Synchronization as one of typical collective behaviors of a dynamical network has been increasingly focused since the latest decades[1-5]. Considering the adverse factors in complex networks, such as transmission delays, controller faults, external disturbances and so on, the synchronization of the complex networks faces enormous challenges[6-9].
As is known, the information transmission over a network with a certain speed may cause time delays, which maybe disturb the stability and connectivity of the complex network. Therefore, the synchronization of complex dynamical networks coupled with time delays has been extensively studied[10-14]. Wang[10] discussed a class of complex interconnected neural networks with delayed and non-delayed coupling and sensor faults, and three kinds of fault tolerant laws are derived to ensure the synchronization of the networks in the presence of delays and sensor faults. The time delays taken into account are invariable[10-13]. But in communications, time delays are often random. Chen[14] proposed a complex dynamical network in which the coupled state information over a network occurs delay randomly, and established synchronization criterion. Therefore, more than fixed delays, random delays should arouse more and more interest of scholars.
In addition to random delays, it is inevitable that external disturbances or uncertainties would affect the synchronization and undermine the stability of the complex dynamical networks. At present, many researchers used some adaptive control methods and external controllers to ensure the synchronization of the complex networks[15-18], which have achieved a great success. For example, the authors designed two adaptive control laws to adjust coupling coefficients and strengths to ensure synchronized states to be stable[16]. In Refs.[16-17], the authors investigated the global synchronization of the complex networks with the delayed and non-delayed coupling by using pinning controllers and adaptive tuning of coupling strength. When these external controllers are required, the control information and measurement information should be conducted by actuators and sensors. However, the control action of actuator and measurement signal of sensor may be affected by the faults, which would destroy the synchronization of the networks. As a result, the actuator and sensor faults should not be ignored for the synchronization of the complex dynamical networks. For the actuator and the sensor faults of networks, fault tolerant control has been an active research topic for enhancing the stability of complex systems and there are a lot of results to be reported[18-19]. There just exist the complex dynamical systems but not the complex dynamical networks in Refs.[18-19], so we can foresee that fault tolerant control is worth studying for the synchronization of the complex networks.
Based on the current research situation, this paper aims to study synchronization for a general complex dynamical network with random delays and sensor faults by using fault tolerant control strategy. In this paper, we consider that the time delays between the network nodes occurs randomly rather than surely, and the random delays are described in the form of Markov chain. Then a synchronization controller is designed to synchronize complex networks. Moreover, sensor faults are considered when designing the synchronization controller because the faults often occurs in many sensors of a complex networks. We have to achieve a reliable synchronization controller to eliminate the effects of the sensor faults and the random delays based on Lyapunov stability theory and stochastic analysis. Thus, the main contribution of this paper is to study fault tolerant synchronization for a complex dynamical network with random delays under the case of sensor faults by designing fault tolerant synchronization controller.
The remainder of the paper is organized as follows. Section 2, a general complex dynamical network with random delays model, assumptions and lemmas are given. In section 3, a passive fault tolerant controller is designed and the main criterion is proposed to achieve the synchronization of the complex dynamical network with random delay in condition of sensor faults. Finally, a numerical example is given in section 4 to demonstrate the effectiveness of the proposed results, and some conclusions are drawn in section 5.
2 PreliminariesConsidering a general complex dynamical network consisting of N identical nodes and coupled with random time delays, which is described by:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_\mathit{\boldsymbol{i}}}\left( t \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \mathit{\boldsymbol{Bf}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) + \sum\limits_{j = 1}^N {{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left[ {\mathit{\delta }\left( t \right){x_j}\left( t \right) + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\left. {\left( {1 - \mathit{\delta }\left( t \right)} \right){x_j}\left( {t - \tau } \right)} \right] \end{array} $ | (1) |
where 1≤i≤N, i≤j≤N, and xi(t)=(xi1(t), xi2(t), …, xin(t))T is the state of ith node at time t; n is the dimension of the node. The constant matrices A and B represent the connection weight matrices with appropriate dimensions, and f=f(xi (t)): Rn→ Rn is a nonlinear function standing for the activity of the node network. The inner coupling matrix Γ=diag (γ11, γ12, …, γ1n) is positive. τ is a constant representing the transmission delay. The outer coupling matrix C represents topological structure of the network. Random variable δ(t)∈[0, 1] is whether the delay happens, which δ(t)=1 indicates that no delay occurs during the transmission of the state xj(t) of the neighbor node j to the node i and δ(t)=0 indicates there is the delay during the transmission.
Remark 1: in the complex network (1), the random variable δ(t) is Markov chain in Ref.[20], and meets an exponential distribution transformation as follows:
| $ \left\{ \begin{array}{l} prob\left\{ {\delta \left( t \right) = 1} \right\} = E\left\{ {\delta \left( t \right)} \right\} = \bar \delta \\ prob\left\{ {\delta \left( t \right) = 0} \right\} = 1 - E\left\{ {\delta \left( t \right)} \right\} = 1 - \bar \delta \end{array} \right. $ | (2) |
Remark 2: for the outer coupling matrix C, if there is a link from node i and node j (i≠j), then cij>0; Otherwise, cij=0. To ensure the existence of synchronization of network (1), assuming that C satisfies the famous diffusive conditions as follows:
| $ {c_{ij}} = {c_{ij}} \ge 0,{c_{ii}} = - \sum\limits_{j = 1,j \ne i}^N {{c_{ij}}} $ | (3) |
Assumption 1[10] The nonlinear function fi(u) is continuous and bounded, and satisfies the following condition:
| $ 0 \le \left( {{\mathit{\boldsymbol{f}}_i}\left( u \right) - {\mathit{\boldsymbol{f}}_i}\left( v \right)} \right)/\left( {u - v} \right) \le {\Delta _i} $ | (4) |
for any u≠v, Δi>0, fi(0)=0, then Δ=diag (Δ1, Δ2, …, Δn).
Lemma 1[20] Let X and Y be real matrices with appropriate dimensions, and P is a positive definite symmetric real matrix. Then for any positive constant ε, matrices X, Y, P satisfy the following inequality:
| $ 2{\mathit{\boldsymbol{X}}^\mathit{\boldsymbol{T}}}\mathit{\boldsymbol{Y}} \le {\varepsilon ^{ - 1}}{\mathit{\boldsymbol{X}}^\mathit{\boldsymbol{T}}}{\mathit{\boldsymbol{P}}^{ - 1}}\mathit{\boldsymbol{X + }}\varepsilon {\mathit{\boldsymbol{Y}}^\mathit{\boldsymbol{T}}}\mathit{\boldsymbol{PY}} $ | (5) |
Lemma 2[21] (Schur complement lemma) Linear matrix inequality as follows:
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{Q}}\left( x \right)}&{\mathit{\boldsymbol{S}}\left( x \right)}\\ {{\mathit{\boldsymbol{S}}^\mathit{\boldsymbol{T}}}\left( x \right)}&{\mathit{\boldsymbol{R}}\left( x \right)} \end{array}} \right] > 0 $ | (6) |
Q(x)=QT(x), R(x)=RT(x). And the linear matrix inequality (6) is equivalent to the following inequalities:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{R}}\left( x \right) > 0\\ \mathit{\boldsymbol{Q}}\left( x \right) - \mathit{\boldsymbol{S}}\left( x \right){\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{S}}^\mathit{\boldsymbol{T}}}\left( x \right) > 0 \end{array} \right. $ | (7) |
In this section, in order to realize the synchronization of the complex dynamical networks (1), the external controller is needed to add on the network, that is,
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_i}\left( t \right) = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \mathit{\boldsymbol{Bf}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) + \sum\limits_{j = 1}^N {{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left[ {\mathit{\delta }\left( t \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( \mathit{\boldsymbol{t}} \right) + } \right.} \\ \;\;\;\;\;\;\;\left. {\left( {1 - \mathit{\delta }\left( t \right)} \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( {t - \tau } \right)} \right] + {\mathit{\boldsymbol{D}}_i}{\mathit{\boldsymbol{u}}_i}\left( t \right) \end{array} $ | (8) |
where 1≤i≤N, Di is a matrix with proper dimensions relating to control channel; ui (t) is the external controller to be designed, and the form of the normal controller is ui(t)=Kixi(t), here Ki is unknown gain matrix.
For the case of the sensor fault, we express the sensor fault matrix as Fi, and the sensor fault description of the ith node network is Fi=diag (fi1, fi2, …, fin). fij=0 denotes that the jth sensor failed in the ith node network, whereas fij=1 denotes the jth sensor is normal. As the sensor faults occurs at the controller, add the sensor faults on the complex dynamical network model (8), we can obtain the following networks form:
| $ \begin{array}{l} {{\mathit{\boldsymbol{\dot x}}}_i}\left( t \right) = \left( {\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{F}}_i}} \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \mathit{\boldsymbol{Bf}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{j = 1}^N {{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left[ {\mathit{\delta }\left( t \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( t \right) + \left( {1 - \mathit{\delta }\left( t \right)} \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( {t - \tau } \right)} \right]} \end{array} $ | (9) |
where 1≤i≤N, the form of the fault tolerant controller is ui(t)=KiFixi(t), here Ki is unknown gain matrix.
Therefore, the following theorem is obtained to achieve the fault tolerant synchronization of the networks (9).
Theorem 1 Supposed that (A, Di) is controllable, if there exist positive definite symmetric matrices Pi, Qi, positive diagonal matrix Si, constants ε1, ε2>0, and matrix Ki, satisfy the conditions as follows:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{11}}}&{{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{B}}}&{{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}}\\ *&{ - {\mathit{\boldsymbol{S}}_\mathit{\boldsymbol{i}}}}&\mathit{\boldsymbol{0}}\\ *&*&{W\mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (10) |
| $ N{\varepsilon _2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\bf{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} - }}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}} < 0 $ | (11) |
where Ω11=Pi(A+DiKiFi)+(A+DiKiFi)TPi+ΔSiΔ+ε1NΓTΓ+Qi; W=-(δ-ε1-1+(1-δ)ε2-1)-1
Proof: Choose the appropriate Lyapunov function candidate for the networks (9) as follows:
| $ \begin{array}{l} V\left( t \right) = \sum\limits_{i = 1}^N {\left[ {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{\boldsymbol{t}} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( \mathit{\boldsymbol{t}} \right) + \int_{t - \tau }^t {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( s \right)} } \right.} {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}\\ \;\;\;\;\;\;\;\;\left. {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( s \right){\rm{d}}s} \right] \end{array} $ | (12) |
Differentiating the V(t) along the solution of the networks (9), we have:
| $ \begin{array}{l} \dot V\left( t \right) = \sum\limits_{i = 1}^N {2\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{\boldsymbol{t}} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\left\{ {\left( {\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{i}}}} \right) + \mathit{\boldsymbol{Bf}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) + } \right.} \\ \;\;\;\;\;\;\left. {\sum\limits_{j = 1}^N {{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left[ {\mathit{\delta }\left( t \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( t \right) + \left( {1 - \mathit{\delta }\left( t \right)} \right){\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{j}}}\left( {t - \tau } \right)} \right]} } \right\} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\left[ {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{\boldsymbol{t}} \right){\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) - \mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( {t - \tau } \right){\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( {t - \tau } \right)} \right]} \end{array} $ | (13) |
Using the assumption 1, we have the following inequalities:
| $ \begin{array}{l} 0 \le \left( {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) - {f_i}\left( 0 \right)} \right)/\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) - 0} \right) \le {\Delta _i} \Rightarrow \\ \;\;\;{\mathit{\boldsymbol{f}}_\mathit{\boldsymbol{i}}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) \le {\Delta _i}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)\\ \;\;\;\therefore {\mathit{\boldsymbol{f}}_\mathit{\boldsymbol{i}}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) \le \Delta {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) \end{array} $ | (14) |
Then based on Lemma 1 and inequality (14), one obtains the following inequalities:
| $ \begin{array}{l} 2\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{Bf}}\left( {{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right) \le 2\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{B \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) \le \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{BS}}_\mathit{\boldsymbol{i}}^{ - 1}{\mathit{\boldsymbol{B}}^{\bf{T}}}\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}^{\bf{T}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right)\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{S}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) \end{array} $ | (15) |
| $ \begin{array}{l} \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {2\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\mathit{\delta }\left( t \right){x_j}\left( t \right) \le } } \\ \;\;\;\;\sum\limits_{i = 1}^N {\left[ {\varepsilon _1^{ - 1}\sum\limits_{j = 1}^N {\mathit{\boldsymbol{x}}_i^{\rm{T}}\left( t \right){\mathit{\boldsymbol{P}}_i}{c_{ij}}\mathit{\delta }\left( t \right)\mathit{\delta }\left( t \right){c_{ij}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} } \right.} \\ \;\;\;\;\left. {\mathit{\boldsymbol{x}}_i^{\rm{T}}\left( t \right){\varepsilon _1}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right] \le \\ \;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right)\left[ {\varepsilon _1^{ - 1}{\mathit{\delta }^2}\left( t \right)\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + {\varepsilon _1}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \right]} {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) \end{array} $ | (16) |
| $ \begin{array}{l} \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {2\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{c_{ij}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {1 - \mathit{\delta }\left( t \right)} \right){x_j}\left( {t - \tau } \right) \le } } \\ \;\;\;\sum\limits_{i = 1}^N {\left[ {\varepsilon _2^{ - 1}\sum\limits_{j = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{c_{ij}}{{\left( {1 - \mathit{\delta }\left( t \right)} \right)}^2}{c_{ij}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + } } \right.} \\ \;\;\;\left. {{\varepsilon _2}\mathit{\boldsymbol{x}}_i^{\rm{T}}\left( {t - \tau } \right)N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( {t - \tau } \right)} \right] \le \\ \;\;\;\sum\limits_{i = 1}^N {\left[ {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right)\varepsilon _2^{ - 1}{{\left( {1 - \mathit{\delta }\left( t \right)} \right)}^2}\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right)} \right.} \\ \;\;\;\left. {\mathit{\boldsymbol{x}}_i^{\rm{T}}\left( {t - \tau } \right){\varepsilon _2}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( {t - \tau } \right)} \right] \end{array} $ | (17) |
Substituting Eqs.(15)-(17) into Eq.(13), one obtains:
| $ \begin{array}{l} \dot V\left( t \right) \le \sum\limits_{i = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right)} \left[ {2{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\left( {\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{i}}}} \right) + {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{BS}}_\mathit{\boldsymbol{i}}^{ - 1}{\mathit{\boldsymbol{B}}^{\bf{T}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\varepsilon _1^{ - 1}{\mathit{\delta }^2}\left( t \right)\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{S}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }} + {\varepsilon _1}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + \\ \;\;\;\;\;\;\;\;\;\left. {\varepsilon _2^{ - 1}{{\left( {1 - \mathit{\delta }\left( t \right)} \right)}^2}\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}} \right]{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( {t - \tau } \right)\left[ {{\varepsilon _2}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} - }}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}} \right]{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( {t - \tau } \right)} \end{array} $ | (18) |
Calculating the mathematical expectation of Eq.(18) by using the Remark 1, that is, E{(1-δ(t))2}=1-δ, one has
| $ \begin{array}{l} E\left( {\dot V\left( t \right)} \right) \le \sum\limits_{i = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( \mathit{t} \right)} \left[ {2{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\left( {\mathit{\boldsymbol{A + }}{\mathit{\boldsymbol{D}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{K}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{F}}_\mathit{\boldsymbol{i}}}} \right) + {\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{BS}}_\mathit{\boldsymbol{i}}^{ - 1}{\mathit{\boldsymbol{B}}^{\bf{T}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon _1^{ - 1}\mathit{\bar \delta }\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{S}}_\mathit{\boldsymbol{i}}}\mathit{\boldsymbol{ \boldsymbol{\varDelta} }} + {\varepsilon _1}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\varepsilon _2^{ - 1}\left( {1 - \mathit{\bar \delta }} \right)\left( {\sum\limits_{j = 1}^N {c_{ij}^2} } \right){\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}}{\mathit{\boldsymbol{P}}_\mathit{\boldsymbol{i}}} + {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}} \right]{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( t \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}^{\bf{T}}\left( {t - \tau } \right)\left[ {{\varepsilon _2}N{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} - }}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}}} \right]{\mathit{\boldsymbol{x}}_\mathit{\boldsymbol{i}}}\left( {t - \tau } \right)} \end{array} $ | (19) |
Based on the Lemma 2, transforming the inequality (19), one has the inequalities (10)-(11) of Theorem 1, then:
| $ E\left( {\dot V\left( t \right)} \right) < 0 $ | (20) |
for any xi(t)≠0, xi(t-τ)≠0;
According to the Lyapunov stability theory, the complex networks (9) realize the synchronization in mean of square by the fault tolerant controller ui(t)=KiFixi(t). Thus, it's obvious that the complex dynamical networks (1) can be synchronized under the fault tolerant controller ui(t)=KiFixi(t) in the case of the sensor faults.
We need to obtain the matrix Ki of the controller, but it's difficult for us to solve directly, as there exist the nonlinear function terms. So we should consider the solubility of result. For the reversibility of Di, the following conditions are given.
If Di is revertible, we let PiDiKi=Yi in the inequality (10), Ki=(PiDi)-1Yi that solved easily.
If Di is not revertible, we assume there exists a revertible matrix H satisfies:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{D}}_i} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{0}} \end{array}} \right]\\ {\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{D}}_i}{\mathit{\boldsymbol{K}}_i} = {\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{H}}^{ - 1}}\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{D}}_i}{\mathit{\boldsymbol{K}}_i} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{P}}_i}{\mathit{\boldsymbol{H}}^{ - 1}}\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{0}} \end{array}} \right]{\mathit{\boldsymbol{K}}_i}{\rm{ = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{11}}}&{{\mathit{\boldsymbol{G}}_{12}}}\\ \mathit{\boldsymbol{0}}&{{\mathit{\boldsymbol{G}}_{22}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_i}}\\ \mathit{\boldsymbol{0}} \end{array}} \right] = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{11}}{\mathit{\boldsymbol{K}}_i}}\\ \mathit{\boldsymbol{0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar Y}}}_i}}\\ \mathit{\boldsymbol{0}} \end{array}} \right] = {\mathit{\boldsymbol{Y}}_i} \end{array} $ |
Then, Theorem 1 can be rewritten to the following Theorem 2.
Theorem 2 Suppose that there exists a revertible matrix H and H satisfies HDi=[I 0]T. If there exists positive definite matrix G, positive diagonal matrix Si, constants ε1, ε2>0, and matrix Ki, satisfies the conditions as follows:
| $ \mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} = }}\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{ \boldsymbol{\bar \varOmega} }}}_{11}}}&{\mathit{\boldsymbol{GHB}}}&{\mathit{\boldsymbol{GH}}}\\ *&{ - {\mathit{\boldsymbol{S}}_\mathit{\boldsymbol{i}}}}&\mathit{\boldsymbol{0}}\\ *&*&{W\mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (21) |
| $ N{\varepsilon _2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\bf{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} - }}{\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{i}}} < 0 $ | (22) |
Thus the complex networks (9) is fault tolerant synchronized in the case of the sensor faults, where Ω11=GHA+ATHTGT+ YiFi+ FiTYiT+ ΔSiΔ +ε1NΓTΓ + Qi, and G=PiH-1, Yi=[Yi 0]T, and the gain matrix Ki=G11-1Yi.
For obtaining a common controller to deal with the sensor faults in every node network, we can let Pi=P, Ki=K, Qi=Q, Si=S, Fi=F, and we can transform Theorem 1 to Corollary 1.
Corollary 1 Supposed (A, D) is controllable, if there exists positive definite symmetric matrices P, Q, positive diagonal matrix S, constants ε1, ε2>0, and matrix K, satisfies the conditions as follows:
| $ \mathit{\boldsymbol{ \boldsymbol{\varOmega} = }}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{11}}}&{\mathit{\boldsymbol{PB}}}&\mathit{\boldsymbol{P}}\\ *&{ - \mathit{\boldsymbol{S}}}&\mathit{\boldsymbol{0}}\\ *&*&{W\mathit{\boldsymbol{I}}} \end{array}} \right] < 0 $ | (23) |
| $ N{\varepsilon _2}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\bf{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} - Q}} < 0 $ | (24) |
Thus the complex networks (9) is fault tolerant synchronized for the sensor faults Fi=F, where Ω11=P(A + DKF)+(A + DKF)T P + ΔSΔ +ε1N Γ T Γ +Q, and * denotes the symmetric parts in the matrix.
4 Numerical SimulationConsider the complex dynamical networks (1) with three nodes. Now we let
When there is no external controller, that is ui(t)=0, and the initial states of nodes condition is x10=(0.2, -0.2)T, x20=(0.6, -0.6)T, x30=(0.9, -0.9)T, the trajectories of the networks are described in Fig. 1, which shows the complex network (1) without controller is out of synchronization. Then, we add the normal controller ui(t)=Kxi(t) to the network (1), and calculate the inequalities of Corollary 1 based on LMI tool, let δ=0.5, ε1=ε2=1, so we have:

|
Figure 1 Trajectories of networks (1) without controller |
| $ \begin{array}{l} \mathit{\boldsymbol{Q}} = {\rm{diag}}\left( {1.5206,1.2673} \right)\\ \mathit{\boldsymbol{S = }}{\rm{diag}}\left( {1.1563,1.1566} \right)\\ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.1620}&{ - 0.0065}\\ { - 0.0065}&{0.0941} \end{array}} \right]\\ \mathit{\boldsymbol{Y = }}\left[ {\begin{array}{*{20}{c}} { - 2.0000}&{0.0032}\\ {0.0032}&{ - 1.8894} \end{array}} \right]\\ \mathit{\boldsymbol{K = }}\left[ {\begin{array}{*{20}{c}} { - 12.3231}&{ - 0.7822}\\ { - 0.8146}&{ - 20.1278} \end{array}} \right] \end{array} $ |
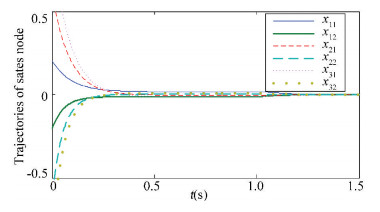
The trajectories of the networks (1) with normal controller ui(t)=Kxi(t) are described in Fig. 2.
|
Figure 2 Trajectories of networks (1) with normal controller |
However, the sensor fault F occurs, the normal controller gain K cannot satisfy the inequalities of Corollary 1. Therefore, based on Corollary 1, for the sensor fault F=diag (0, 1), the gain of the fault tolerant controller is:
| $ \mathit{\boldsymbol{K'}} = {\left( {\mathit{\boldsymbol{PD}}} \right)^{ - 1}}\mathit{\boldsymbol{Y = }}\left[ {\begin{array}{*{20}{c}} { - 79.7726}&{ - 2.1809}\\ { - 2.8270}&{ - 87.7130} \end{array}} \right] $ |
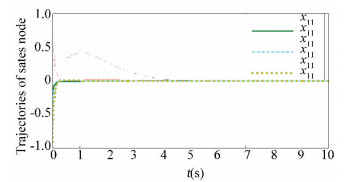
The sensor fault F=diag (0, 1) occurs in the first node network, the state trajectories of the networks (1) with the fault tolerant controller ui(t)=K'Fxi(t) are shown in Fig. 3.
|
Figure 3 Trajectories of networks (1) with fault tolerant controller for F=diag (0, 1) occurs in the first node network |
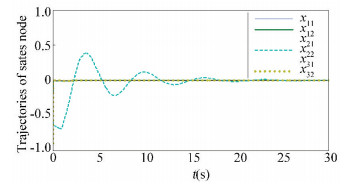
Similarly, the sensor fault F=diag (1, 0) occurs in the second node network, the state trajectories of the networks (1) with fault tolerant controller are shown in Fig. 4.
|
Figure 4 Trajectories of networks (1) with fault tolerant controller for F=diag (1, 0) occurs in second node network |
From Figs. 3 and 4, we can observe that the node network achieve the synchronization, which tests the effectiveness of Corollary 1's results.
From the example simulation, we can realize that effectiveness of the fault tolerant synchronization method for the synchronization of the general complex dynamical networks with random delays and the sensor faults proposed in this paper. Due to the existing literature just study the synchronization problem for a complex network only with random delay or just with network sensor faults. Compared with these existing literatures, we consider the random factors of the network delays and the fault factors exist in sensors of the networks simultaneously, and achieve the fault tolerant synchronization of the complex networks finally. Thus, achieving the synchronization of the complex networks in condition of these adverse factors in this paper has more practical significance and extensive application.
5 ConclusionsThis paper discussed the fault tolerant synchronization for a general complex dynamical network with random delays and sensor faults. The passive tolerant synchronization criterion is derived in the form of matrix inequality, and the example demonstrates its effectiveness. Moreover, the similar results can be obtained for the case of actuator faults. In addition, the synchronization of this paper occurs in a complex network, it's possible that the fault tolerant synchronization occurs in two complex networks, that is, the drive-response networks, which is worth studying.
| [1] |
Wang X, Chen G. Synchronization in small-world dynamical networks.
International Journal of Bifurcation and Chaos, 2002, 12(01): 187-192.
DOI:10.1142/S0218127402004292 ( 0) 0)
|
| [2] |
Fan J, Wang X. On synchronization in scale-free dynamical networks.
Physica A: Statistical Mechanics and Its Applications, 2005, 349(3): 443-451.
( 0) 0)
|
| [3] |
Batista C A S, Batista A M, de Pontes J A C, et al. Chaotic phase synchronization in scale-free networks of bursting neurons.
Physical Review E, 2007, 76(1): 016218.
DOI:10.1103/PhysRevE.76.016218 ( 0) 0)
|
| [4] |
Chen M, Zhou D. Synchronization in uncertain complex networks.
Chaos, 2006, 16(1): 013101-1.
DOI:10.1063/1.2126581 ( 0) 0)
|
| [5] |
Hu G, Yang J, Liu W. Stability and controllability of coupled oscillators.
Physical Review E, 1998, 58(4): 4440.
DOI:10.1103/PhysRevE.58.4440 ( 0) 0)
|
| [6] |
Xiao Y, Xu W, Tang S, et al. Adaptive complete synchronization of the noise-perturbed two bi-directionally coupled chaotic systems with time-delay and unknown parametric mismatch.
Applied Mathematics and Computation, 2009, 213(2): 538-547.
DOI:10.1016/j.amc.2009.03.049 ( 0) 0)
|
| [7] |
Gau R S, Lien C H, Hsieh J G. Novel stability conditions for interval delayed neural networks with multiple time-varying delays.
International Journal of Innovative Computing, Information and Control, 2011, 7(1): 433-444.
( 0) 0)
|
| [8] |
Zhao J, Hill D J, Liu T. Synchronization of complex dynamical networks with switching topology: A switched system point of view.
Automatica, 2009, 45(11): 2502-2511.
DOI:10.1016/j.automatica.2009.07.013 ( 0) 0)
|
| [9] |
Lü J, Chen G. A time-varying complex dynamical network model and its controlled synchronization criteria.
IEEE Transactions on Automatic Control, 2005, 50(6): 841-846.
DOI:10.1109/TAC.2005.849233 ( 0) 0)
|
| [10] |
Wang Z, Li T, Zhang H. Fault tolerant synchronization for a class of complex interconnected neural networks with delay.
International Journal of Adaptive Control and Signal Processing, 2014, 28: 859-881.
DOI:10.1002/acs.2399 ( 0) 0)
|
| [11] |
Li C, Xu H, Liao X, et al. Synchronization in small-world oscillator networks with coupling delays.
Physica A: Statistical Mechanics and its Applications, 2004, 335(3/4): 359-364.
DOI:10.1016/j.physa.2003.12.037 ( 0) 0)
|
| [12] |
Li C, Chen G. Synchronization in general complex dynamical networks with coupling delays.
Physica A: Statistical Mechanics and Its Applications, 2004, 343: 263-278.
DOI:10.1016/j.physa.2004.05.058 ( 0) 0)
|
| [13] |
Li C P, Sun W G, Kurths J. Synchronization of complex dynamical networks with delays.
Physica A: Statistical Mechanics and Its Applications, 2006, 361(1): 24-34.
DOI:10.1016/j.physa.2005.07.007 ( 0) 0)
|
| [14] |
Chen M. Synchronization in complex dynamical networks with random sensor delay.
IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2010, 57(1): 46-50.
DOI:10.1109/TCSII.2009.2037258 ( 0) 0)
|
| [15] |
Zhao Y, Jiang G J. Fault diagnosis for a class of output-coupling complex dynamical networks with time delay.
Acta Physica Sinica, 2011, 11: 006.
( 0) 0)
|
| [16] |
Guo W, Austin F, Chen S, et al. Pinning synchronization of the complex networks with non-delayed and delayed coupling.
Physics Letters A, 2009, 373(17): 1565-1572.
DOI:10.1016/j.physleta.2009.03.003 ( 0) 0)
|
| [17] |
Yu W, Chen G, Lv J. On pinning synchronization of complex dynamical networks.
Automatica, 2009, 45(2): 429-435.
DOI:10.1016/j.automatica.2008.07.016 ( 0) 0)
|
| [18] |
Liu M, Shi P, Zhang L. Fault tolerant control for nonlinear Markovian jump systems via proportional and Derivative sliding mode observer technique.
IEEE Transactions on Circuits and Systems I: Regular Papers, 2011, 58(11): 2755-2764.
DOI:10.1109/TCSI.2011.2157734 ( 0) 0)
|
| [19] |
Gao Z, Jiang B, Shi P. Passive fault tolerant control design for the near space hypersonic vehicle dynamical system.
Circuits, Systems and Signal Processing, 2012, 31(2): 565-581.
DOI:10.1007/s00034-011-9385-7 ( 0) 0)
|
| [20] |
Gong D, Zhang H, Wang Z, et al. Novel synchronization of an uncertain complex networks with hybrid coupling by handling multitude Kronecker product terms.
Neurocomputing, 2012, 82: 14-20.
DOI:10.1016/j.neucom.2011.09.026 ( 0) 0)
|
| [21] |
Lin C, Wang Z, Yang F. Observer-based networked control for continuous-time systems with random sensor delays.
Automatica, 2009, 45(2): 578-584.
DOI:10.1016/j.automatica.2008.09.009 ( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


