The Wireless Sensor Network (WSN) has been widely employed for many real life applications, such as disaster prevention, biological environment and medical monitoring[1]. These applications demands for the reliability during transmission of data across WSN as well as energy efficiency of the network. The basic idea of virtual cooperative MIMO relies on the studies performed by Dohler et al[2]. on the virtual antenna array (VAA) in the 4G technology. Recently, many virtual cooperative MIMO schemes for transmission have been proposed [3-12].
Some representatives of researchers on the establishment of the model for the system's energy consumption analysis, such as Cui et al.[3] from Standford, proposed a classic virtual cooperative MIMO transmission scheme on the basis of Alamouti space-time coding and variable modulation constellation, and established the corresponding model for the analysis of node and system energy consumption. Jayaweera[4] extended the energy consumption calculation model in Ref.[3] to include the extra energy overheads caused by the channel training sequence. They also analyzed energy effectiveness of the MIMO technology and the dependency relationship between the coherence time of fading channel and the number of channel training sequences.
In terms of the routing protocol that combines the cluster with the cooperative MIMO technology, Li et al.[5] suggested a cooperative MIMO scheme for transmission that combines the LEACH protocol with the STBC coding principles, and discussed the requirements on synchronization between intra-cluster cooperative nodes. Yuan et al.[6-7] proposed a distributed multi-hop routing protocol based on the LEACH protocol and the cooperative MIMO technology. Xu et al.[8] proposed an improved routing protocol for tackling the issue of neglecting channel training sequence as per the study mentioned in Ref. [5] and the issue of performance slump in the case of a long distance from the base station to the sensor network as described in Ref. [6]. To defeat the issues in Ref.[6] that the cluster heads are not distributed evenly due to random selection of the cluster head and the cluster count is not necessarily equal to the optimal cluster count in the network, Zhou et al.[9] proposed an improved semi-centralized control scheme, where the base station serves as the command center to appoint certain network nodes as the clusters through calculation. Li[10] proposed a novel virtual-MIMO communication approach on the basis of a cooperative group.Li[11] presented a novel approach for energy-efficient transmission of data on the basis of virtual MIMO and DSC. Yang[12] proposed an approach for heterogeneous WSN called V-BLAST, the approach is based on a cooperative MIMO scheme for transmission.
To sum up, in most of the works about the cluster-based WSN that relies on cooperative MIMO communication, energy optimization is performed by adopting the same transmission parameters throughout the entire network. That is, the communication between all virtual MIMO units and the sink node has the same cooperative node count and the modulation speed. However, the distance space of the cluster head of the virtual MIMO unit and the sink node varies greatly among different virtual MIMO units. The cooperative node count and the speed of modulation with varying communication distance have a large influence on consumption of energy for the cooperative MIMO system. Hence, the parameters used for communicating should be adapted to the communication distance for minimizing consumption of energy.
In the current study, we suggest a cluster-based virtual cooperative MIMO scheme for transmission (CVCM). The optimal cooperative node count and the optimal speed of modulation are dynamically determined on the basis of the distance space for the cluster head and the sink node for the purpose of minimizing consumption of energy caused by communication between each virtual MIMO unit and the sink node and maximizing the life duration of the network.
2 System ModelTo facilitate discussions below, the following assumptions on the system model are made:
1) N sensor nodes are evenly disseminated among a square region size of M×M. The sensor nodes have the same original energy and the energy cannot be replenished.
2) There are few constraints on the energy and hardware resources of the sink nodes that function as the gateway.
3) For the intra-cluster short-distance transmission, the additive Gaussian white noise channel, which fades in a square-law manner, is adopted as the channel model with a modulation scheme called binary phase shift keying (BPSK).
4) The kth-order Rayleigh flat fading signal model is used for the long-distance communication between the cooperative nodes and also for the long-distance communication between the nodes labeled as cooperative and the sink, with a modulation scheme called quadrature amplitude modulation (MQAM), assuming the channel of each node is mutually independent.
5) The communication happens in the high SNR (Signal to Noise Ratio) region.
6) In order to prevent the model from being overcomplicated, we choose to ignore the consumption of energy of the module for processing the baseband signals for coding, pulse shaping and digital modulation.
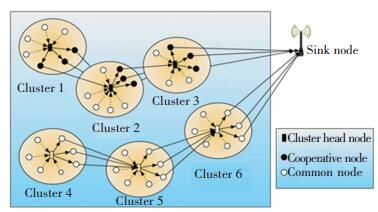
The proposed CVCM is illustrated in Fig. 1. The data transmission process of CVCM can be described with the concept "round" like LEACH and each round involves phases for setup and transmission.
|
Figure 1 The suggested cluster-based virtual cooperative MIMO scheme for transmission |
The former phase involves selecting the cluster head, formation of virtual MIMO unit (cluster) and the selection of cooperative node. The transmission phase is mainly responsible for the intra-cluster data transmission, fusion of data for the cluster head, and cooperative transmission of data from the cluster head (virtual MIMO unit) to the sink node. Due to the limit of space, procedures of the setup and transmission phases are not detailed here.
2.1 Cooperative Node Selection ProcessDuring the cooperative MIMO transmission process, the common node may transmit data to the node labeled as cluster head and be selected as the cooperative node to participate in long-distance cooperative communication, which all consumes energy. In order to avoid the same node is repeatedly selected as the collaborative node, due to excessive energy consumption and premature death, affecting the network life cycle, so the choice of cooperative nodes is very important.
In this paper, the residual energy and transmission distance are taken as the important basis for the selection of cooperative nodes. We adopt a cooperative node selection strategy with maximum residual energy and minimum transmission power. That is to say, a node that is close to the next-hop cluster head node and whose transmission power is less will be selected as the cooperative node in the common nodes with more residual energy. The cooperative node decision threshold is determined as:
| $ \delta = \frac{{{E_{{\rm{remain\_}}i}}}}{{{P_{r\_i}}}} $ |
where Eremain_i is the remaining energy of the member node, and Pr_i is the power transmitted by the node to the next-hop node labeled as cluster head.
It calculates the values of the threshold according to its own residual energy and estimated transmit power. Then it reports the threshold to the cluster head node before each round of data transmission. The cluster head node is responsible for selecting the nodes (Mr) with the largest threshold δ from all the members to participate in the cooperative communication. On completion of the respective round of the data transmission, the member node sends the updated value to the node labeled as cluster head to ensure the real-time threshold of cluster head record.
The system's overall energy consumption model needs to be established first in order to optimize network parameters. Based on the communication model in Fig. 1, the system's energy consumption is to be divided into two parts:
1) Local communication-induced energy consumption (EL): it includes the energy consumption EL-T required for data transmission between the intra-cluster node and the node labeled as cluster head and also between the node labeled as cluster head and the node labeled as cooperative, as well as the circuit-induced energy EL-C consumed during the transmission process.
2) Remote communication-induced energy consumption (ER): it includes the energy consumption ER-T required for intra-cluster communication when the node labeled as cooperative sends the data to the next-hop node labeled as cluster head, and the circuit-induced energy consumption ER-C.
They can be written as:
| $ \left\{ \begin{array}{l} {E_L} = {E_{L\_T}} + {E_{L\_C}}\\ {E_R} = {E_{R\_T}} + {E_{R\_C}} \end{array} \right. $ |
During the local communication (such as the intra-cluster data transmission) process, the consumption of energy mainly consists of the local transmission-induced consumption of energy EL-T and the circuit-induced consumption of energy EL-C. They can be expressed as:
| $ \left\{ \begin{array}{l} {E_{{\rm{L}}\_{\rm{T}}}} = {k_{\rm{c}}}\left( {{E_{{\rm{T\_mtoCH}}}} + {E_{{\rm{T}}\_{\rm{CHtoc}}}}} \right)\\ {E_{{\rm{L}}\_{\rm{C}}}} = {k_{\rm{c}}}\left( {{E_{{\rm{C\_mtoCH}}}} + {E_{{\rm{C}}\_{\rm{CHtoc}}}}} \right) \end{array} \right. $ |
where ET_mtoCH denotes the energy consumption required by the intra-cluster sensor nodes to converge data collected to the node labeled as cluster head; ET_CHtoc denotes the energy consumption required to broadcast the data to cooperative transmission nodes after data fusion at the cluster head; EC_mtoCH denotes the total amount of energy consumption required by the intra-cluster sensor nodes to converge the collected data to the cluster head; and EC_CHtoc denotes the total amount of energy consumption required by the node labeled as cluster head to broadcast the fused data to nodes for cooperative transmission, kc is the optimal number of clusters.
With BPSK adopted here as the modulation scheme, the average bit error rate of the receiver is
| $ Q\left( {\sqrt 2 \gamma } \right) = \frac{1}{2}erfc\left( {\sqrt \gamma } \right) = \frac{1}{{\sqrt {\rm{\pi }} }}\int_{\sqrt \gamma }^\infty {{e^{ - {z^2}}}{\rm{d}}z} $ |
According to the previous assumptions 3) (the intra-cluster communication channel is the additive Gaussian white noise channel that fades in a square-law manner), γ can be expressed as:
| $ \gamma = \frac{{{P_{{\rm{r\_mtoCH}}}}}}{{2B{\sigma ^2}{N_f}}} $ |
Here Pr_mtoCH refers to the power of the signal received by the node; σ2=N0/2 denotes the AGWN channel power spectrum density under the normal temperature; and Nf refers to the noise coefficient of the receiver. According to the Chernoff upper bound, when the network is in the high SNR ratio, the average bit error rate can be approximated as:
| $ \overline {{P_b}} = Q\left( {\sqrt 2 \gamma } \right) \le {e^{ - \gamma }} $ |
Pr_mtoCH can be written as:
| $ {P_{{\rm{r\_mtoCH}}}} = - 2B{\sigma ^2}{N_f}\ln \left( {\overline {{P_b}} } \right) $ |
Hence, we have
| $ {P_{{\rm{t\_mtoCH}}}} = {P_{{\rm{r\_mtoCH}}}}{G_d} = - 2B{\sigma ^2}{N_f}\ln \left( {\overline {{P_b}} } \right) \times {G_d} $ |
Here Gd refers to the square-law fading component and Gd=G1dmtoCH2Ml, G1 is the power gain component at d= 1 m; Ml denotes the coefficient of compensation for link fading; dmtoCH gives the average distance between nodes labeled as the intra-cluster sensor node and the cluster head node.
Ordinarily, the cluster is likely to take on any shape. However, for presenting the analysis in this paper, we presume it as round[13] with an average radius
| $ \begin{array}{*{20}{c}} {E\left[ {d_{{\rm{mtoCH}}}^2} \right] = \int_0^{\frac{M}{{\sqrt {{\rm{\pi }}{k_c}} }}} {\int_0^{\frac{M}{{\sqrt {{\rm{\pi }}{k_c}} }}} {\left( {{x^2} + {y^2}} \right)\rho \left( {x,y} \right){\rm{d}}x{\rm{d}}y = } } }\\ {\int_0^{2{\rm{\pi }}} {\int_0^{\frac{M}{{\sqrt {{\rm{\pi }}{k_c}} }}} {{r^3}\rho \left( {r,\theta } \right){\rm{d}}r{\rm{d}}\theta } } } \end{array} $ | (1) |
The uniform distribution of the nodes implies that its distribution density is constant. Hence, Eq.(1) can be simplified as:
| $ E\left[ {d_{{\rm{mtoCH}}}^2} \right] = = \rho \int_0^{2{\rm{\pi }}} {\int_0^{\frac{M}{{\sqrt {{\rm{\pi }}{k_c}} }}} {{r^3}{\rm{d}}r{\rm{d}}\theta } } = \frac{{{M^2}}}{{2{\rm{\pi }}{{\rm{k}}_c}}} $ |
The average distance between the nodes labeled as intra-cluster sensor node and the cluster head node can be computed as :
| $ {d_{{\rm{mtoCH}}}} = M/\sqrt {{\rm{2\pi }}{k_c}} $ |
Here, the numerical value of the bandwidth is equal to the transmission rate of BPSK used as modulation scheme. Hence, the time needed for the sensor node ni to transmit L-bit data at a probability of P is Ton, i=LPi/B. Moreover, the total amount of energy consumption needed to transmit the data from the node labeled as intra-cluster sensor node to the cluster head node can be described as follows. (Note that the data reception-induced energy consumption at the cluster head is ignored here to simplify calculations.)
| $ \begin{array}{l} {E_{{\rm{T\_mtoCH}}}} = \left( {1 + \alpha } \right)\sum\limits_{i = 1}^{N/{k_c} - 1} {{P_{{\rm{t\_mtoCH}}}} \times {T_{{\rm{on}},i}}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - 2\left( {1 + \alpha } \right)\sum\limits_{i = 1}^{N/{k_c} - 1} {{\sigma ^2}{N_f}\ln \left( {\overline {{P_b}} } \right){G_d}L{P_i}} \end{array} $ | (2) |
For Eq.(2), we have:
| $ 1 + \alpha = \frac{\xi }{\eta } = \frac{3}{\eta }\left( {\frac{{{2^{b/2}} - 1}}{{{2^{b/2}} + 1}}} \right) $ |
where α refers to the utility component of the radio frequency power amplifier. It is depended on the specific scheme for modulation and the modulation constellation; η refers to the drain efficiency of the radio frequency power amplifier; b refers to the size of the modulation constellation, and b= 1 here due to the use of BPSK; ξ refers to the peak-to-average ratio (PAR) of the modulated symbol.
After receiving the collected data from intra-cluster nodes, the node labeled as cluster head fuses the received data firstly for broadcasting it to the nodes labeled as cooperative. Except the only difference in the amount of transmitting data, the consumption of energy at this phase is analyzed as mentioned above, with ET_CHtoc denoting the data transmission-induced energy consumption.
The post-fusion data size depends on the correlation between the data to be fused, which is described here using the data fusion model proposed in Ref.[14]. The post-fusion data at the cluster head is expressed as below:
| $ {L_{{\rm{agg}}}} = \left( {\sum\limits_{i = 1}^{N/{k_c} - 1} {L{P_i}} } \right)/\left( {{f_{{\rm{agg}}}}\sum\limits_{i = 1}^{N/{k_c} - 1} {{P_i} - {f_{{\rm{agg}}}} + 1} } \right) $ |
where fagg is the data fusion factor and its range is (0, 1).
To guarantee that the data broadcasted by the cluster head can be received by Mr intra-cluster cooperative nodes, the effective communication range of the cluster head during the broadcasting process is defined as the maximum distance dmax between all nodes and the node labeled as cluster head. Hence, the total consumed energy at this phase can be expressed as follows. Note that the data reception-induced energy consumption at the cooperative node is ignored here to simplify calculation.
| $ {E_{{\rm{T\_CHtoc}}}} = - 2\left( {1 + \alpha } \right){\sigma ^2}{N_f}\ln \left( {\overline {{P_b}} } \right){G_1}d_{\max }^2{M_l}{L_{{\rm{agg}}}} $ | (3) |
As shown in Ref.[3], the circuit consumption of energy mainly involves the consumption of energy in transmitting circuit PL_ct and the receiving circuit PL_cr.
PL_ct can be written as:
| $ {P_{{\rm{L\_ct}}}} \approx {P_{{\rm{mix}}}} + {P_{{\rm{filt}}}} + {P_{{\rm{syn}}}} $ |
where Pmix, Pfilt, Psyn respectively, as the mixer, the transmitter filtering, frequency synthesizer module power consumption.
| $ {P_{{\rm{L\_cr}}}} \approx {P_{{\rm{LNA}}}} + {P_{{\rm{mix}}}} + {P_{{\rm{IFA}}}} + {P_{{\rm{filr}}}} + {P_{{\rm{syn}}}} $ |
Here PLNA, PIFA, Pfilr, Psyn are refers to power consumption of low-noise amplifier, mixer, IF amplifier, filtering and the receiver frequency synthesizer.
According to Fig. 1, the consumption of circuit energy can be described as:
| $ {E_{{\rm{C\_mtoCH}}}} = \left( {\sum\limits_{i = 1}^{N/{k_c} - 1} {{P_{{\rm{L\_ct}}}} + {P_{{\rm{L\_cr}}}}} } \right) \times {T_{{\rm{on}},i}} $ | (4) |
| $ {E_{{\rm{C}}\_{\rm{CHtoc}}}} = \left( {{P_{{\rm{L\_ct}}}} + {M_r}{P_{{\rm{L\_cr}}}}} \right)\frac{{{L_{{\rm{agg}}}}}}{B} $ | (5) |
On the receipt of the data broadcasted by the cluster head, the intra-cluster cooperative nodes will perform distributed STBC coding of the fused data and then transmit the data. Because the data transmission between the cooperative node and the next-hop cluster head is long-distance transmission, MQAM is used in this paper as the scheme for modulation in order to reduce the delay in transmission & consumption of the circuit-induced energy further. As each of the cooperative nodes is ignorant of the situation on average fading of the channel to the next-hop cluster head, the scheme of assigning equal transmission power to each cooperative node is adopted[15]. The channel between the nodes labeled as cooperative and the sink is the kth-order Rayleigh flat fading channel (k= 4 in this paper). As per Free-Space link propagation model, the data transmission-induced energy consumption at each node labeled as cooperative can be modeled as below:
| $ {P_{{\rm{T\_ctoNCH}}}} = \overline {{E_b}} {R_b}\frac{{4{{\rm{\pi }}^2}d_{{\rm{ctoNCH}}}^k{M_l}{N_f}}}{{{G_t}{G_r}{\lambda ^2}}} \times \frac{1}{{{M_r}}} $ |
where Rb denotes the data transmission rate under MQAM (Rb=bB when the modulation order b≥2); dctoNCH gives the average distance between all cooperative nodes and the node labeled as next-hop cluster head; Gt denotes the antenna gain of transmission; Gr denotes the antenna gain for reception, and λ denotes the carrier's wavelength;
| $ \overline {{E_b}} = {M_r} \times \frac{2}{3}{\left( {\frac{{\overline {{P_b}} }}{4}} \right)^{ - \frac{1}{{{M_r}}}}} \times \frac{{{2^b} - 1}}{{{b^{\frac{1}{{{M_r}}} + 1}}}} \times {N_0} $ | (6) |
Based on the slow fading assumption on the channel[16], supposing that the channel state stays the same for transmitting a set of F symbols and there are pMr channel training symbols in this set of symbols, where p denotes the number of symbols used to train each transmitting-receiving antenna pair, the effective transmission rate of the channel, Rbeff can be written as Rbeff=(F-pMr)RRb/F, where R denotes the STBC coding rate. In this context, the time required for transmitting Lagg-bit fused data to the node labeled as next-hop cluster head is
| $ {T_{{\rm{ON}}}} = {L_{{\rm{agg}}}}/R_b^{{\rm{eff}}} $ |
Finally, by considering Eqs.(4) and (6) jointly, it can be known that the energy consumption required by the node labeled as cooperative to transmit the data to the node labeled as next-hop cluster head is
| $ \begin{array}{l} {E_{{\rm{T\_ctoNCH}}}} = {M_r}\left( {1 + \alpha } \right){P_{{\rm{T\_ctoNCH}}}}{T_{{\rm{ON}}}} = {M_r} \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{3}{\eta }\left( {\frac{{{2^{b/2}} - 1}}{{{2^{b/2}} + 1}}} \right) \times {P_{{\rm{T\_ctoNCH}}}} \times {L_{{\rm{agg}}}}/R_b^{{\rm{eff}}} \end{array} $ |
Finally, the energy required to pass the data to the sink node along the minimum-energy transmission path is:
| $ {E_{{{R\_T}}}} = H \cdot {E_{{\rm{T\_ctoNCH}}}} $ | (7) |
where H denotes the number of hopes required to deliver the data to the sink node along the minimum-energy transmission path, as per experimental results in Ref.[13], the average number of hops that the data arrives at the sink node is
Due to the assumption that there is no energy constraint on the sink node, the circuit-induced energy consumption at the sink node is ignored in the total amount of circuit-induced energy consumption. Hence, in the long-distance communication phase, the circuit-induced energy consumption of each hope of data transmission is
| $ {E_{{\rm{C\_ctoNCH}}}} = {M_r} \times {P_{{\rm{L\_ct}}}}{L_{{\rm{agg}}}}/R_b^{{\rm{eff}}} $ |
Similarly, the total amount of circuit-induced energy consumption at the long-distance communication phase is
| $ {E_{{\rm{R\_C}}}} = H \cdot {E_{{\rm{C\_ctoNCH}}}} $ | (8) |
We suggest a joint consumption of energy optimization model of the system on the basis of above analysis. The optimal network parameters of the CVCM scheme can be determined by solving this model.
Based on Eqs.(2)-(5) and (7)-(8) the total amount of energy consumed by the system during a cycle in CVCM is
| $ \begin{array}{l} {E_{{\rm{total}}}}\left( {{k_c},b,{M_r}} \right) = {E_{L\_T}} + {E_{L\_C}} + {E_{R\_T}} + {E_{R\_C}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{k_c}\left( {{E_{{\rm{T\_mtoCH}}}} + {E_{{\rm{T\_CHtoc}}}} + {E_{{\rm{C\_mtoCH}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{E_{{\rm{C}}\_{\rm{CHtoc}}}}} \right) + H\left( {{E_{{\rm{T\_ctoNCH}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{E_{{\rm{C\_ctoNCH}}}}} \right) \end{array} $ |
By combining and simplifying these equations, it can be noticed that the total energy consumption of the system is a function of three variables, namely the cluster count, kc, the order of modulation, b, and the cooperative node count, Mr. The optimal values of these parameters can be computed while minimizing the total consumption of energy.
For the real-world wireless sensor network, the modulation order b is usually set to an even number, such as 2, 4, 6 and 8. Although a high value of the modulation order means higher transmission speed and lesser circuit-induced energy consumption, the transmission power of the amplifier increases in order to ensure bit error rate, resulting in greater energy consumption of the system overall. Hence, it is set to a value no larger than 14 in this paper. Similarly, as proven in some literatures, more cooperative nodes will not necessarily bring the better work due to the corresponding increase in the circuit-induced energy consumption, which leads to more consumption of energy the overall system. Hence, the consumption of energy optimization model of CCVM can be established as:
| $ \begin{array}{l} \left( {{k_c},b,{M_r}} \right) = \arg \min {E_{{\rm{total}}}}\left( {{k_c},b,{M_r}} \right)\\ \;\;\;\;\;\;\;\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\;{\rm{2}} \le {M_r} \le 12\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2 \le {k_c} \le N/{M_r}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2 \le b \le 14 \end{array} $ | (9) |
The optimization problem described in Eq.(9) can be considered as an integer programming problem[17]. Mature algorithms are available to solve this optimization problem. Because the search space of the model in this paper is not large, we choose to solve the model using the method of exhaustion. In the real-world network implementation, the optimal network parameters can be determined by measuring and computing the parameters beforehand and then programming the parameters into the nodes.
3 Simulation Results and Analysis 3.1 Environmental Parameter SettingsIn order to illustrate the transmission performance of the proposed scheme called CVCM, extensive simulation experiments have been performed via MATLAB, and the simulation results are analyzed thoroughly. Basic simulation parameters of the system are depicted in Table 1.
| Table 1 Parameter setting values for simulations |
The compared methods include the LEACH routing protocol and the EBMH (cluster-based non-cooperative) routing protocol in Ref.[18]. Consider that 300 sensor nodes are disseminated randomly across the sensing region of size 200 m×200 m, with the same energy originally. Other parameter settings of the system are shown in Table 1. Major performance metrics are network lifetime, total consumption energy of the system, and the effective packet count received by the base station.
3.2 Influence of Parameters kc, b, and Mr on the Total Consumption of Energy by the System1) Influence of b on the total amount of energy consumption of the system
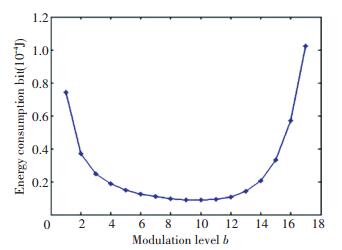
Many experiments indicate that the cluster count kc and the cooperative node count Mr have little influence on the modulation order b. Fig. 2 shows the influence of the modulation order b on the total consumption energy of the system in the case of kc=15 and Mr=2.
|
Figure 2 Influence of the modulation level b on the total consumption of energy |
Fig. 2 shows that the system's total consumption of energy varies greatly with the increase of modulation order b and it reaches the lowest level when b= 5.
2) Influence of kc and Mr on the total consumption of energy by the system
Fig. 3 depicts the influence of kc and Mr on the total consumption of energy by the system as per the proposed CVCM scheme. The following observations emerge from this figure.

|
Figure 3 Influence of kc and Mr on the total consumption of energy by the system |
(1) The total consumption of energy by the system varies greatly with the increase in the number of clusters, and it reaches the lowest level when kc=5.
(2) The number of cooperative nodes has little influence on the system's total consumption of energy. And the consumption of energy by the system can be optimized when Mr=2 or 3. As discussed above, it has been proven that the increased cooperative nodes will enlarge the system's circuit-induced energy consumption correspondingly, resulting in higher amount of energy consumption in the system overall.
3.3 Simulation Results and AnalysisBased on the discussions above, the performance of LEACH, EBMH and CVCM are compared on the basis of network life time, total consumption of energy by the system, and the effective packet count received by the base station.
1) Network lifetime
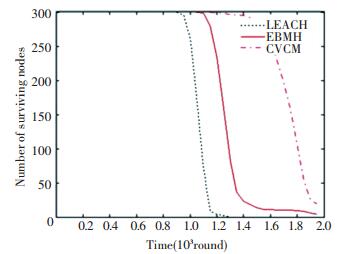
Fig. 4 provides the comparison the surviving node count under three protocols. This figure implies that compared with LEACH and EBMH, CVCM greatly increases the network lifetime, because of the use of the cooperative MIMO communication strategy. Detailed comparisons with LEACH are given in Table 2. It can be seen that when half of the nodes are dead, the network lifetime of CVCM is longer than LEACH by 65% and EBMH by 19.1%.
|
Figure 4 Comparison of the number of surviving nodes under the three protocols |
| Table 2 Network lifetime as a function of the node count |
2) Energy consumption of the system
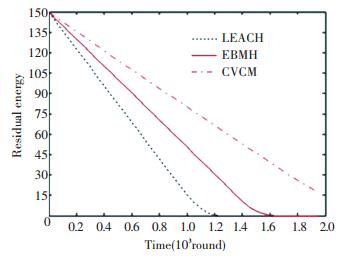
Fig. 5 shows the residual network energy as a function of the time. The steeper the curve, the faster the network consumes the energy. If the curve changes slowly, it means that the network energy is consumed slowly; the network lifetime is longer; and the network's energy consumption is more balanced. For example, by the 1 000th round of network operation, the remaining energy of the network under LEACH has been small (about 15 J or 10% of the original energy). But the remaining energy of the network under EBMH is still very large (about 80 J or 53.3% of the initial energy). The remaining energy of the network under CVCM is lower than that under EBMH (about 50 J).
|
Figure 5 Comparison of the residual network energy under the three protocols |
3) Receiving of effective packets by the base station[20]
Fig. 6 shows that CVCM enables the base station to receive the highest number of effective packets, followed by EBMH immediately and then LEACH. This is due to the fact that instead of directly transmitting the data after clustering, CVCM transmits the data to the base station through cooperative communication. This figure also shows that the amount of data that can be transmitted effectively via CVCM increases with time.
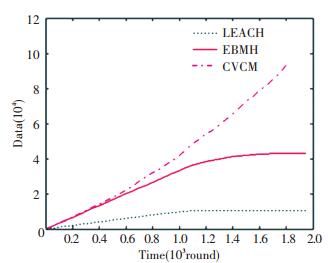
|
Figure 6 Variation of the effective packet count received by the base station |
4 Conclusions
A cluster-based cooperative MIMO transmission scheme called CVCM is suggested in this paper. An end-to-end optimization model for consumption of energy by the system is established to determine the network parameters that can minimize the consumption of energy for the entire network. The optimal cooperative node count and the optimal modulation rate are obtained in CVCM according to the distance space between the nodes labeled as cluster head and the sink node. By following the strategy of maximizing the residual energy and minimizing the transmission power, the cooperative node is chosen to guarantee that the communication-induced energy consumption of each cooperative unit and the sink node is minimized to lengthen the network lifetime as long as possible. Simulation results prove that, the proposed CVCM scheme achieves enormous performance gain, effectively lengthens the survival time of the node, increases the network lifetime, and improves the effectiveness of data reception at the base station in comparison to LEACH and EBMH.
| [1] |
Zhang Y, Xiang S, Fu W, et al. Improved normalized collinearity DV-Hop algorithm for node localization in wireless sensor network.
International Journal of Distributed Sensor Networks, 2014, 2014(11): 1-14.
DOI:10.1155/2014/436891 ( 0) 0)
|
| [2] |
Dohler M, Lefranc E, Aghvami H. Space-time block codes for virtual antenna arrays.
The IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, 2002, 1: 414-417.
DOI:10.1109/PIMRC.2002.1046733 ( 0) 0)
|
| [3] |
Cui S, Goldsmith A J, Bahai A. Energy-efficiency of MIMO and cooperative MIMO techniques in sensor networks.
IEEE Journal on Selected Areas in Communications, 2004, 22(6): 1089-1098.
DOI:10.1109/JSAC.2004.830916 ( 0) 0)
|
| [4] |
Jayaweera S K. Virtual MIMO-based cooperative communic-ation for energy-constrained wireless sensor networks.
IEEE Transactions on Wireless Communications, 2006, 5(5): 984-989.
DOI:10.1109/TWC.2006.1633350 ( 0) 0)
|
| [5] |
Li X H, Chen M, Liu W. Application of STBC-encoded cooperative transmissions in wireless sensor networks.
IEEE Signal Processing Letters, 2005, 12(2): 134-137.
DOI:10.1109/LSP.2004.840870 ( 0) 0)
|
| [6] |
Yuan Y, He Z, Chen M. Virtual MIMO-based cross-layer design for wireless sensor networks.
IEEE Transactions on Vehicular Technology, 2006, 55(3): 856-864.
DOI:10.1109/TVT.2006.873837 ( 0) 0)
|
| [7] |
Yuan Y, Chen M, Kwon T. A novel cluster-based cooperative MIMO scheme for multi-hop wireless sensor networks.
EURASIP Journal on Wireless Communications and Networking, 2006(2): 38-38.
DOI:10.1155/WCN/2006/72493 ( 0) 0)
|
| [8] |
Xu K, Liu W, Yang Z. An End-to-end optimized cooperative transmission scheme for virtual MIMO sensor networks. Proceedings of the 200610th IEEE Singapore International Conference on Communication Systems.
Piscataway:IEEE, 2006: 1-5.
DOI:10.1109/ICCS.2006.301370 ( 0) 0)
|
| [9] |
Zhou P, Pei X, Xu K. A Semi-centralized approach for optimized multihop virtual MIMO wireless sensor networks. Proceedings of the International Conference on Communications and Networking.
Piscataway:IEEE, 2007: 877-881.
DOI:10.1109/CHINACOM.2007.4469524 ( 0) 0)
|
| [10] |
Li B, Zheng G, Li N, et al. A virtual MIMO communication strategy based on cooperative groups for wireless sensor networks.
International Journal of Future Generation Communication & Networking, 2015, 8(3): 223-234.
DOI:10.14257/ijfgcn.2015.8.3.21 ( 0) 0)
|
| [11] |
Li N, Zhang L, Li B. A new energy-efficient data transmission scheme based on DSC and virtual MIMO for wireless sensor network.
Journal of Control Science & Engineering, 2015, 2015: 1-9.
DOI:10.1155/2015/904274 ( 0) 0)
|
| [12] |
Yang Guangyou, Li Jun, Gan Xiong. A V-BLAST-Based cooperative MIMO transmission scheme for heterogeneous wireless sensor networks. Proceedings of the Internet and Distributed Computing Systems. IDCS 2016. Springer International Publishing. Berlin: Springer, 2016, 9864: 477-486. DOI:10.1007/978-3-319-45940-0_44.
( 0) 0)
|
| [13] |
Heinzelman W B, Chandrakasan A P, Balakrishnan H. An application-specific protocol architecture for wireless micro sensor networks.
IEEE Transactions on Wireless Communications, 2002, 1(4): 660-670.
DOI:10.1109/TWC.2002.804190 ( 0) 0)
|
| [14] |
Chebolu M L, Jayaweera S K. Integrated design of STBC-based virtual-MIMO and distributed compression in energy-limited wireless sensor networks.
Wireless Sensor Networks, Second European Workshop, EWSN, 2005, 2005: 267-277.
DOI:10.1109/EWSN.2005.1462019 ( 0) 0)
|
| [15] |
Chen W, Yuan Y, Xu C, et al. Virtual MIMOprotocol based on clustering for wireless sensor network. Proceedings of the 10th IEEE Symposium on Computers and Communications.
Piscataway:IEEE, 2005: 335-340.
DOI:10.1109/ISCC.2005.154 ( 0) 0)
|
| [16] |
Garcia-Rodriguez A, Masouros C. Exploiting the increasing correlation of space constrained massive MIMO for CSI relaxation.
IEEE Transactions on Communications, 2016, 64(4): 1572-1587.
DOI:10.1109/TCOMM.2016.2538222 ( 0) 0)
|
| [17] |
Chen S G. Proceedings of the 2013 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM).
Piscataway:IEEE, 2013: 98-100.
DOI:10.1109/IEEM.2013.6962382 ( 0) 0)
|
| [18] |
Lyu H F, Zhang H. Energy-balanced multi-hop routing protocol among clusters.
Information and Control, 2014, 43(3): 306-313.
DOI:10.3724/SP.J.1219.2014.00306 ( 0) 0)
|
| [19] |
Singh D P, Bhateja V, Soni S K. Energy optimization in WSNs employing rolling grey model. Proceedings of the International Conference on Signal Processing and Integrated Networks.
Piscataway:IEEE, 2014: 801-808.
DOI:10.1109/SPIN.2014.6777064 ( 0) 0)
|
| [20] |
Hong Z, Wang R, Li X. A clustering-tree topology control based on the energy forecast for heterogeneous wireless sensor networks.
IEEE/CAA Journal of Automatica Sinica, 2016, 3(1): 68-77.
DOI:10.1109/JAS.2016.7373764 ( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


