The traditional finite element analysis (FEA) is performed under the condition that the input parameters are all deterministic. However, the geometrical dimensions, material properties, boundary conditions are always uncertain in engineering. The ability to handle uncertainties is significant for a design engineer. The probabilistic concept which is applied in the different fields has caused increasing criticism in the last decade due to the limited statistical information on uncertainties[1]. The subjective results may be obtained by the probabilistic method[2], which proves to be time-consuming[3-6]. Additionally, a significant problem related with the probabilistic method is that the probability distribution should be predicted based on a large amount of statistical information, while the information corresponding to uncertainties is usually hard to obtain[7-8].
In this context, non-probabilistic concepts have been introduced. Interval and fuzzy approaches are attracting more and more attention for the uncertainty analysis and optimization of numerical models in their descriptions. In the past decades, the interval and fuzzy concepts in FEA have been studied extensively and some typical solution schemes for the interval FEA (IFEA) and fuzzy FEA (FFEA) have been developed[9-10]. In the interval method, uncertainties are assumed to be varied within a bounded range and only the interval bounds are necessary for the uncertain parameter. The fuzzy approach extends this method with the help of α-level technique. Therefore, the fuzzy approach needs the consecutive solution for many interval analysis based on the α-level technique[11]. From this view, current researches on non-probabilistic uncertainty propagation are mainly focused on the implementation and solution of the interval analysis.
The purpose of this work is to give an overview of recent developments related with numerical implementations of IFEA and FFEA in the field of applied mechanics. The goal of FFEA is to formulate the fuzzy description of FEA results. The intersection with the membership function related to uncertainties on each α-level leads to an interval. IFEA is then formulated, which results in an interval for the output on each α-level. The IFEA aims to capture the bounds of specific output quantities of interest based on a given interval description of input uncertainties. For the sake of simplicity, the static analysis of a mechanical system is adopted in this paper to explain current IFEA schemes.
When facing the case in which the slight parameter fluctuates, the uncertain parameter vector α is modeled as an uncertain-but-bounded vector. Each element of the vector is defined in an uncertain but bounded real set. According to interval theory, αc and Δα denote the nominal value and radius of the uncertain vector α as follows:
| $ {\mathit{\boldsymbol{\alpha }}^{\rm{c}}} = \frac{{{\mathit{\boldsymbol{\alpha }}^{\rm{L}}} + {\mathit{\boldsymbol{\alpha }}^{\rm{U}}}}}{2},\Delta \mathit{\boldsymbol{\alpha = }}\frac{{{\mathit{\boldsymbol{\alpha }}^{\rm{U}}} + {\mathit{\boldsymbol{\alpha }}^{\rm{L}}}}}{2} $ |
where αU and αL are the upper and lower bounds of the uncertain vectors. Thus, interval vector is expressed as follows:
| $ {\mathit{\boldsymbol{\alpha }}^{\rm{I}}} = \left[ {\mathit{\boldsymbol{\underline \alpha }} ,\mathit{\boldsymbol{\overline \alpha }} } \right] = \left\{ {\mathit{\boldsymbol{\alpha }}\left| {\mathit{\boldsymbol{\underline \alpha }} \le \mathit{\boldsymbol{\alpha }} \le } \right.\mathit{\boldsymbol{\overline \alpha }} } \right\} = {\mathit{\boldsymbol{\alpha }}_0} + \Delta \mathit{\boldsymbol{\alpha }}{\mathit{\boldsymbol{e}}^I} $ | (1) |
where eiI=[-1, 1] and its values are unknown but assumed to lie in the unitary interval. The component form of Eq.(1) can be written as:
| $ {\alpha _i} = a_i^c + \Delta {\alpha _i}e_i^I $ |
where aic and Δαi represent the nominal value and radius of the i-th interval variable, respectively and they are depicted in Fig. 1.
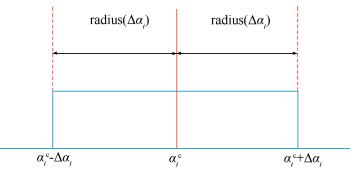
|
Figure 1 The diagram of uncertain variable α |
The FEA equation in a general form can be shown as follows:
| $ \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{\alpha }} \right)\mathit{\boldsymbol{U}}\left( \mathit{\boldsymbol{\alpha }} \right) = \mathit{\boldsymbol{F}}\left( \mathit{\boldsymbol{\alpha }} \right) $ |
where K and F represent the stiffness matrix and load vector, respectively; U denotes the static response vector; α is the vector of input parameter from the mechanical system.
Accordingly, the general form of IFEA equation is derived as follows:
| $ \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right)\mathit{\boldsymbol{U}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right) = \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right) $ |
in which the superscript 'I' denotes an interval input.
The exact solution set of the above interval equation is shown as:
| $ \mathit{\boldsymbol{U = }}\left\{ {{\mathit{\boldsymbol{U}}^ * }\left| {\mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^ * }} \right){\mathit{\boldsymbol{U}}^ * } = \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^ * }} \right),\forall {\mathit{\boldsymbol{\alpha }}^ * } \in {\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right.} \right\} $ | (2) |
Generally, the interdependencies among entries of the response vector are introduced due to sharing the common input vector. A non-convex polyhedron is always defined, which makes it hard to obtain the exact solution[12]. Nevertheless, only individual bounds of part of components deserve to be obtained in actual problems. Therefore, the smallest hypercube approximation denoted as UI around the exact solution set can be served as an alternative object for current IFEA when neglecting the aforementioned interdependencies. From this view, the kth component of UI can be written as follows:
| $ \begin{array}{l} \mathit{\boldsymbol{U}}_k^{\rm{I}} = \left[ {U_k^{\rm{L}},U_k^{\rm{U}}} \right] = \left[ {\mathop {\min }\limits_{\alpha \in {\alpha ^I}} {U_k}\left( \mathit{\boldsymbol{\alpha }} \right),\mathop {\max }\limits_{\alpha \in {\alpha ^{\rm{I}}}} {U_k}\left( \mathit{\boldsymbol{\alpha }} \right)} \right],\\ \;\;\;\;\;\;\;k = 1,2, \cdots ,N \end{array} $ |
where U and L stand for the upper and lower bounds, respectively. N is the total number of response components of interest. Therefore, the smallest hypercube solution of IFEA equation can be expressed as:
| $ {\mathit{\boldsymbol{U}}^{\rm{I}}} = {\left[ {U_1^{\rm{I}},U_2^{\rm{I}}, \cdots ,U_{\rm{N}}^{\rm{I}}} \right]^{\rm{T}}} $ |
where T is a transposition operator.
The relationship between input uncertain parameters and output displacement response is illustrated in Fig. 2.
|
Figure 2 Schematic diagram of the uncertainty propagation process |
2 Pre-processing Technique 2.1 Surrogate Model Technique
To enhance the efficiency of IFEA and FFEA, many surrogate models of the real numerical model are always adopted when dealing with large-scale FEA models. Apart from the conventional surrogate models used in the optimization procedure of IFEA and FFEA, e.g. response surface models[13-14], Kriging models[15-17], radial basis function models[18-20] and sparse grid meta-models[21-23], those for the sampling and optimization approaches including the high dimensional model representation (HDMR) and the component mode synthesis (CMS) are gaining momentum in recent years.
CMS is originally introduced in which the Ritz-type transformation is adopted[24]. By virtue of a lower number of component modes, the deformation of each component can be approximated. Only a single degree of freedom appears in the reduced component model for each of these vectors, which leads to a big reduction DOF for the entire structure. Therefore, the computational cost for the FEA is drastically reduced. From this viewpoint, CMS can also be seen as a special surrogate model of the expensive numerical FEA for the improvement in the computational efficiency. The repeated FEAs required in the context of IFEA can benefit from this computational time reduction obtained by CMS.
2.2 Subinterval TechniqueFor the accuracy improvement, the subinterval technique with respect to interval inputs is developed[25] and can be integrated with the perturbation approaches, which greatly relaxes requirements of 'small' or 'narrow' interval inputs for nonlinear responses. The methods for determining the subinterval number are investigated in Ref.[26]. However, there remain two challenges as follows:
1) Convergence validation
Similar to the prior determination of the sample size of Monte Carlo method in the probabilistic analysis, the subinterval number for each interval parameter should be firstly determined to guarantee the convergence of the analysis result.
2) Efficiency sacrifice
An exponential increase of the computational cost is introduced as increasing the subinterval number to guarantee the convergence of the analysis result. For example, the computational cost increases by mn times where n denotes the number of parameters and m stands for the number of subintervals for each interval parameter. Thus, the most dominant advantage in efficiency for the perturbation approaches over other interval algorithms is significantly sacrificed.
3 Main Algorithms 3.1 Optimization ApproachThe optimization approach can return the interval bounds of the response of a general FEA model through an optimization algorithm within the domain spanned by interval parameters. The smallest hypercube solution around the exact one can thus be determined if the global maximum and minimum of the responses are obtained using the optimization algorithm. The directional search based algorithm[27-28], and genetic algorithm[29] are utilized to formulate the procedure of IFEA or FFEA. More applications can be found in Ref.[30]. It should be noted that the optimization method can be adopted to verify the accuracy of other schemes for IFEA and FFEA. Generally, the optimization approach is undertaken on each element of the vector of response independently. The optimization strategy can approach the smallest hypercube solution from its inside. Thus, the conservatism is not guaranteed until the actual bounds are captured. Moreover, the computational cost of the optimization approach is strongly problem-dependent because the behavior of the target response corresponding to the uncertain parameter is unpredictable. Therefore, the optimization approach can be applied for the lower-dimensional natural characteristic analysis of simple structures. Additionally, the smooth behavior of the target response with respect to uncertain parameters makes it possible to search for the global extrema over the space determined by uncertain parameters.
Thus, the solution set of Eq.(2) can be expressed as follows:
| $ \mathit{\boldsymbol{U}} = \left\{ {\begin{array}{*{20}{c}} {{U_1}}\\ {{U_2}}\\ \vdots \\ {{U_N}} \end{array}} \right\} \in \left\{ {\begin{array}{*{20}{c}} {\left[ {U_1^{\rm{L}},U_1^{\rm{U}}} \right]}\\ {\left[ {U_2^{\rm{L}},U_2^{\rm{U}}} \right]}\\ \vdots \\ {\left[ {U_N^{\rm{L}},U_N^{\rm{U}}} \right]} \end{array}} \right\} $ |
with
| $ \begin{array}{l} U_k^{\rm{L}}, = \mathop {\min }\limits_{\alpha \in {\alpha ^I}} {U_k}\left( \mathit{\boldsymbol{\alpha }} \right),k = 1,2, \cdots ,N\\ U_k^{\rm{U}} = \mathop {\max }\limits_{\alpha \in {\alpha ^{\rm{I}}}} {U_k}\left( \mathit{\boldsymbol{\alpha }} \right),k = 1,2, \cdots ,N \end{array} $ |
The perturbation approach has been widely applied in structural static and dynamic response analyses and other applications. Compared to optimization approach, perturbation methods are more popular due to its simplicity and efficiency in IFEA and can be available in the original and improved versions.
3.2.1 Original versionUsing the first-order Taylor expansion method, the stiffness matrix and load vector with consideration of the interval vector are derived as:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right) = \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right) + \sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}} = {\mathit{\boldsymbol{K}}^{\rm{c}}} + \Delta {\mathit{\boldsymbol{K}}^{\rm{I}}}} \\ \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right) = \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right) + \sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}} = {\mathit{\boldsymbol{F}}^{\rm{c}}} + \Delta {\mathit{\boldsymbol{F}}^{\rm{I}}}} \end{array} \right. $ | (3) |
where αc is the nominal value of the interval input vector and ΔαiI=[-Δαi, Δαi] is the interval radius of the ith interval parameter, i.e.
| $ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}^{\rm{c}}} = \left( {{\mathit{\boldsymbol{\alpha }}^{\rm{U}}} + {\mathit{\boldsymbol{\alpha }}^{\rm{L}}}} \right)/2 = {\left[ {\alpha _1^{\rm{c}},\alpha _2^{\rm{c}}, \cdots ,\alpha _n^{\rm{c}}} \right]^{\rm{T}}}\\ \Delta \mathit{\boldsymbol{\alpha }} = \left( {{\mathit{\boldsymbol{\alpha }}^{\rm{U}}} - {\mathit{\boldsymbol{\alpha }}^{\rm{L}}}} \right)/2 = {\left[ {\Delta {\mathit{\boldsymbol{\alpha }}_1},\Delta {\mathit{\boldsymbol{\alpha }}_2}, \cdots ,\Delta {\mathit{\boldsymbol{\alpha }}_n}} \right]^{\rm{T}}} \end{array} $ |
and the interval radiuses shown in Eq.(3) can be expressed as:
| $ \left\{ \begin{array}{l} \Delta {\mathit{\boldsymbol{K}}^{\rm{I}}} = \sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}}} = \left[ { - \Delta \mathit{\boldsymbol{K}},\Delta \mathit{\boldsymbol{K}}} \right]\\ \Delta {\mathit{\boldsymbol{F}}^{\rm{I}}} = \sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}}} = \left[ { - \Delta \mathit{\boldsymbol{F}},\Delta \mathit{\boldsymbol{F}}} \right] \end{array} \right. $ | (4) |
The FEA model for the perturbed system are given by the following form as:
| $ \left( {{\mathit{\boldsymbol{K}}^{\rm{c}}} + \Delta {\mathit{\boldsymbol{K}}^{\rm{I}}}} \right)\left( {{\mathit{\boldsymbol{U}}^{\rm{c}}} + \Delta {\mathit{\boldsymbol{U}}^{\rm{I}}}} \right) = {\mathit{\boldsymbol{F}}^{\rm{c}}} + \Delta {\mathit{\boldsymbol{F}}^{\rm{I}}} $ | (5) |
By expanding Eq.(5) and neglecting the second-order perturbed term, the following equations can be obtained as:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{U}}^{\rm{c}}} = {\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{c}}}\\ {\mathit{\boldsymbol{K}}^{\rm{c}}}\Delta {\mathit{\boldsymbol{U}}^{\rm{I}}} = \Delta {\mathit{\boldsymbol{F}}^{\rm{I}}} - \Delta {\mathit{\boldsymbol{K}}^{\rm{I}}}{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{c}}} \end{array} \right. $ | (6) |
Substituting Eq.(4) into Eq.(6), the interval radius of the displacement vector is derived as:
| $ \begin{array}{l} \Delta {\mathit{\boldsymbol{U}}^{\rm{I}}} = {\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}}\sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}}} - \\ \;\;\;\;\;\;\;\;\;\;\;{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}}\sum\limits_{i = 1}^n {\frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}\Delta \alpha _i^{\rm{I}}{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{c}}}} \end{array} $ |
and the radius vector can be estimated with the help of the original interval perturbation method[31-32] as follows:
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \sum\limits_{i = 1}^n {\left( {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}} \right|\left| {\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}} \right| + } \right.} \\ \;\;\;\;\;\;\;\;\;\left. {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}} \right|\left| {\frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}} \right|\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}} \right|\left| {{\mathit{\boldsymbol{F}}^{\rm{c}}}} \right|} \right)\Delta {\alpha _i} \end{array} $ |
The smallest hypercube solution can thus be determined as:
| $ {\mathit{\boldsymbol{U}}^{\rm{I}}} = \left[ {{\mathit{\boldsymbol{U}}^{\rm{c}}} - \Delta \mathit{\boldsymbol{U}},{\mathit{\boldsymbol{U}}^{\rm{c}}} + \Delta \mathit{\boldsymbol{U}}} \right] $ | (7) |
It is noted that a significant overestimation can be introduced by the original interval perturbation method, which indicates that it is suitable for the interval analysis of problems with 'small' interval parameters.
3.2.2 Improved versionThe most typical improved interval perturbation method is proposed in Ref.[33], in which the radius vector of the response vector is calculated as follows:
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \\ \;\;\sum\limits_{i = 1}^n {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}{\mathit{\boldsymbol{F}}^{\rm{c}}}} \right|\Delta {\alpha _i}} \end{array} $ | (8) |
Accordingly, the smallest hypercube solution of IFEA can be determined by Eq.(8). Although with better accuracy compared to the original one, an interval translation effect, i.e. the translation of the resulting interval corresponding to the accurate one, is always introduced by the improved interval perturbation method.
Compared with the original version of the perturbation approach where only first-order terms are considered, the main aspect of the following modified interval perturbation methods is that the interval bounds are calculated by retaining part of higher order terms in Neumann series. Two other modified interval perturbation methods are recently proposed in Refs.[34-37] and key expressions are summarized as follows:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{U}}^{\rm{c}}} = {\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}}\left[ {\mathit{\boldsymbol{I + }}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{E}}_i^{\rm{c}}} } \right]{\mathit{\boldsymbol{F}}^{\rm{c}}}\\ \Delta {\mathit{\boldsymbol{U}}^{\rm{I}}} = \sum\limits_{k = 1}^n {\left\{ {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\left[ {\mathit{\boldsymbol{I + }}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{E}}_i^{\rm{c}}} } \right]\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _k}}}} \right\}} \Delta \alpha _k^{\rm{I}} + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\Delta \mathit{\boldsymbol{E}}_i^{\rm{I}}{\mathit{\boldsymbol{F}}^{\rm{c}}}} \end{array} $ |
where
| $ \begin{array}{l} \mathit{\boldsymbol{E}}_i^{\rm{c}} = \left( {{{\left( {\mathit{\boldsymbol{I + }}\Delta {\alpha _i}{\mathit{\boldsymbol{K}}_i}} \right)}^{ - 1}} + {{\left( {\mathit{\boldsymbol{I}} - \Delta {\alpha _i}{\mathit{\boldsymbol{K}}_i}} \right)}^{ - 1}} - 2\mathit{\boldsymbol{I}}} \right)/2\\ \;\;\;\;\Delta {\mathit{\boldsymbol{E}}_i} = \left| {{{\left( {\mathit{\boldsymbol{I + }}\Delta {\alpha _i}{\mathit{\boldsymbol{K}}_i}} \right)}^{ - 1}} - {{\left( {\mathit{\boldsymbol{I}} - \Delta {\alpha _i}{\mathit{\boldsymbol{K}}_i}} \right)}^{ - 1}}} \right|/2 \end{array} $ |
and
| $ {\mathit{\boldsymbol{K}}_i} = \frac{{\partial \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _i}}}{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)^{ - 1}} $ |
Different estimations of the radius vector of the response vector are obtained as follows:
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \left| {\sum\limits_{k = 1}^n {\left\{ {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\left[ {\mathit{\boldsymbol{I + }}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{E}}_i^{\rm{c}}} } \right]\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _k}}}} \right\}\Delta {\alpha _k}} + } \right.\\ \;\;\;\;\;\;\;\;\left. {\sum\limits_{i = 1}^n {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\Delta {\mathit{\boldsymbol{E}}_i}{\mathit{\boldsymbol{F}}^{\rm{c}}}} } \right\} \end{array} $ | (9) |
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \sum\limits_{k = 1}^n {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\left[ {\mathit{\boldsymbol{I + }}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{E}}_i^{\rm{c}}} } \right]\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\mathit{\boldsymbol{\alpha }}_k}}}} \right|\Delta {\alpha _k}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^n {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\Delta {\mathit{\boldsymbol{E}}_i}{\mathit{\boldsymbol{F}}^{\rm{c}}}} \right|} \end{array} $ | (10) |
It should be pointed out that a significant unpredicted estimation is introduced by Eq.(9) and Eq.(10). A more reasonable estimation of the radius vector of the response vector is simultaneously determined herein as follows:
| $ \begin{array}{l} \Delta \mathit{\boldsymbol{U}} = \sum\limits_{k = 1}^n {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}\left[ {\mathit{\boldsymbol{I + }}\sum\limits_{i = 1}^n {\mathit{\boldsymbol{E}}_i^{\rm{c}}} } \right]\frac{{\partial \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{c}}}} \right)}}{{\partial {\alpha _k}}}} \right|\Delta {\alpha _k}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^n {\left| {{{\left( {{\mathit{\boldsymbol{K}}^{\rm{c}}}} \right)}^{ - 1}}} \right|\Delta {\mathit{\boldsymbol{E}}_i}\left| {{\mathit{\boldsymbol{F}}^{\rm{c}}}} \right|} \end{array} $ | (11) |
and a slight conservatism is alternatively resulted in by Eq.(11). Therefore, the smallest hypercube solution for the IFEA is finally determined as Eq.(7).
It is worth mentioning that a prior requirement for the aforementioned interval perturbation methods is that the spectral radius of (Kc)-1ΔK is less than unity. Therefore, these methods can be applied to the interval analysis of nonlinear problems with 'small' uncertain variables and the accuracy for those with 'large' interval inputs can be improved by the subinterval technique in Section 4.2.
3.3 Sampling Approach 3.3.1 Vertex methodThe vertex method is firstly proposed in Ref.[38], which can be seen as a sampling technique with vertices being input samples of the FEA model. This method has been popular for the implementation of IFEA due to its simple formulation and the black-box property. The vertex method can be applied for the structural strength, stability, and natural characteristic analysis of complex structures in the fields of mechanics, aviation, shipping, etc[39-44]. If the target response corresponding to uncertain parameters is verified to be monotonic, the exact solution can be yielded by the vertex method. However, the property of monotonicity is generally hard to be proved monotonic especially within the scope of structural dynamics[45].
The number of FEA runs necessary is determined as:
| $ N = {2^n} $ |
where n is the number of interval parameters. It is noted that the computational afford for the vertex method increases exponentially with the number of interval parameters, which leads a dimensionality curse.
3.3.2 Transformation methodTo increase the accuracy of the vertex method, transformation methods for the uncertainty propagation are developed aiming at solving the non-monotonic problems[46]. This method is on the basis of the α-level strategy and the interval problem is defined according to each α-level. A dedicated sampling strategy is composed of the interval solution strategy in the space spanned by α-cut of fuzzy parameters. This method can be obtained in three types of form, including the general, reduced and extended form. Each form can be selected appropriately according to the evaluated type of model[47]. If the behavior of the target response corresponding to uncertain parameters is verified to be monotonic, the exact solution can be yielded by the reduced transformation method. If the non-monotonic behavior is shown, the extended transformation method is suitable for this problem. In this method, more observation points are added in a well-directed way to the search domain based on a classification criterion.
The computational afford of the transformation method can be calculated based on the number of FEA runs N. As for the case of the general transformation method, N can be derived as follows:
| $ N = \sum\limits_{k = 1}^{m + 1} {{k^n}} $ |
where m and n are the number of discrete α-levels and fuzzy parameters, respectively. It should be noted that the FEA runs N increases exponentially versus the number of fuzzy inputs, which makes the general transformation method hard to solve the high dimensional problems. Moreover, by reducing the fuzzy arithmetic to multiple crisp-number operations, the transformation method can be applied to an existing software environment without major problems and does not require the repeated writing of the program codes[48]. Some of the most recent applications can be found in Refs.[49-51]. Besides, a program named Fuzzy Arithmetical Modeling of Uncertain Systems is created to provide an interface to software environments.
4 Hybrid Algorithms 4.1 Surrogate Model Based Hybrid AlgorithmsA method named as Taylor expansion with extrema management is proposed by integrating the higher-order Taylor series expansion and the optimization approach[52] to search possible non-monotonic influences. A component mode transformation method is developed[53] by combing the CMS with the transformation method to reduce the computational cost for large uncertain mechanical problems. Besides, a hybrid method[54] is proposed to implement the frequency response analysis with interval parameters by integrating the optimization approach. The computational cost is shown to be acceptable and the amount of conservatism in the analysis result can be limited by utilizing these hybrid algorithms.
4.2 Subinterval-based Hybrid AlgorithmsDivide the large interval parameter αiI(i=1, 2, …, n) into Ni subintervals and its ri-th subinterval can be expressed as follow:
| $ \begin{array}{l} {\left( {\alpha _i^{\rm{I}}} \right)_{{r_i}}} = \left[ {\alpha _i^{\rm{I}} + \frac{{2\left( {{r_i} - 1} \right)\Delta {\alpha _i}}}{{{N_i}}},\alpha _i^{\rm{L}} + \frac{{2{r_i}\Delta {\alpha _i}}}{{{N_i}}}} \right],\\ \;\;\;\;\;\;\;\;\;{r_i} = 1,2, \cdots ,{N_i} \end{array} $ |
The number of subintervals may be different for each interval parameter. The combinations Nsub is obtained by selecting a subinterval from each interval parameter
| $ {N_{{\rm{sub}}}} = \prod\limits_{i = 1}^n {{N_i}} $ |
For each subinterval combination, the IFEA model can be rewritten as:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_n}}^{\rm{I}}} \right)\mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_n}}^{\rm{I}}} \right) = \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_n}}^{\rm{I}}} \right),}\\ {{r_i} = 1,2, \cdots ,{N_i};i = 1,2, \cdots ,n} \end{array} $ | (12) |
where αr1r2…rnI represents a subinterval combination and is formulated by the r1-th subinterval of the first interval parameter, the r2-th subinterval of the second one and up to the rn-th subinterval of the nth one. Accordingly, Eq.(12) represents for Nsub subinterval IFEA equations. For each subinterval IFEA equation, the response vector can be obtained by using main algorithms in section 2, e.g. interval perturbation approaches, sampling approaches. For two adjacent subinterval vector αr1…rr…rnI and αr1…rr+1…rnI, the following formulae holds true, i.e.
| $ \begin{array}{l} \mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} \cdots {r_n}}^{\rm{I}}} \right) \cap \mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} + 1 \cdots {r_n}}^{\rm{I}}} \right) = \mathit{\boldsymbol{K}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}}^{\rm{I}}, \cdots ,\alpha _{{r_r}}^{\rm{U}} = } \right.\\ \;\;\;\;\;\left. {\alpha _{{r_r} + 1}^{\rm{L}}, \cdots ,\alpha _n^{\rm{I}}} \right)\\ \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} \cdots {r_n}}^{\rm{I}}} \right) \cap \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} + 1 \cdots {r_n}}^{\rm{I}}} \right) = \mathit{\boldsymbol{F}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}}^{\rm{I}}, \cdots ,\alpha _{{r_r}}^{\rm{U}} = } \right.\\ \;\;\;\;\;\left. {\alpha _{{r_r} + 1}^{\rm{L}}, \cdots ,\alpha _n^{\rm{I}}} \right) \end{array} $ |
where αrrU stands for the upper bound of αrrI while αrr+1L represents the lower bound of αrr+1L. Thus, the intersection of U(αr1…rr…rnI) and U(αr1…rr+1…rnI) does not return an empty set, i.e.
| $ \mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} \cdots {r_n}}^{\rm{I}}} \right) \cap \mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1} \cdots {r_r} + 1 \cdots {r_n}}^{\rm{I}}} \right) \ne \emptyset $ | (13) |
It is shown from Eq.(13) that the interval response vectors for each subinterval combination are simply connected. Therefore, the interval response vector is derived based on the following interval union operation:
| $ \begin{array}{l} \mathit{\boldsymbol{U}}\left( {{\mathit{\boldsymbol{\alpha }}^{\rm{I}}}} \right) = \mathop \cup \limits_{\begin{array}{*{20}{c}} {{r_i} = 1,2, \cdots ,{N_i}}\\ {i=1,2, \cdots ,n} \end{array}} \mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_i} \cdots {r_n}}^{\rm{I}}} \right) = \\ \;\;\;\left[ {\mathop {\min }\limits_{{r_i} = 1,2, \cdots ,{N_i}} \left( {\mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_i} \cdots {r_n}}^{\rm{I}}} \right)} \right),\mathop {\max }\limits_{{r_i} = 1,2, \cdots ,{N_i}} \left( {\mathit{\boldsymbol{U}}\left( {\mathit{\boldsymbol{\alpha }}_{{r_1}{r_2} \cdots {r_i} \cdots {r_n}}^{\rm{I}}} \right)} \right)} \right] \end{array} $ |
The subinterval technique and Taylor series expansion are integrated in Ref.[25]. More applications can be found in Refs.[55-56].
4.3 Hybrid Main AlgorithmsThe aforementioned main algorithms can be combined together to achieve a better tradeoff between the accuracy and efficiency, e.g. frameworks[57-58] formulated by the global optimization methods and interval perturbation ones. To improve the computational efficiency, any main algorithm in Section 2 can be integrated with re-analysis method[59] which is fundamentally an intrusive FEA. It is noted that the major computational cost of IFEA consists of repeated solutions of the deterministic FEA systems while the re-analysis method aims at accelerating this conventional FEA solution process. It is shown that applying the re-analysis method in the IFEA make contributions to reducing the computational afford by one order of magnitude compared to those based on the conventional FEA strategy.
5 ConclusionsThe recent advances in non-probabilistic finite element analyses are presented in this paper. The main advantages and disadvantages of each non-probabilistic FEA method are investigated. The optimization approach is served as standard procedure in the IFEA except for the high computational cost. Due to its simplicity and efficiency, the perturbation approach has been widely applied in structural analyses and other related fields.
The accuracy of the original perturbation methods can be improved by retaining part of higher order terms in Taylor series or Neumann series as shown in the improved and modified versions. The sampling approach like the vertex method yields the exact solution under the condition that the behavior of the target response versus uncertain parameters can be verified to be monotonic and has been popular for the implementation of IFEA due to its main aspect of simple formulation and the black-box property. However, when tackling the non-monotonic problems, the extended transformation methods should be applied by adding more observation points in a well-directed way. Moreover, in this context, two typical pre-processing procedures, e.g. surrogate model and subinterval technique to improve either the accuracy or efficiency are described in detail. Additionally, hybrid algorithms, including surrogate model based hybrid algorithms, subinterval-based hybrid algorithms, and hybrid main algorithms can be conceived by combining the aforementioned main algorithms and pre-processing procedures to achieve a better tradeoff between the accuracy and efficiency for the specific problems and the future work in this research field can be promoted.
| [1] |
Ben-Haim Y, Elishakoff I.
Convex Models of Uncertainty in Applied Mechanics. Amsterdam: Elsevier Science Publishers, 1990.
( 0) 0)
|
| [2] |
Elishakoff I. Essay on uncertainties in elastic and viscoelastic structures: From A. M. Freudenthal's criticisms to modern convex modeling.
Computers & Structures, 1995, 56(6): 871-895.
DOI:10.1016/0045-7949(94)00499-S ( 0) 0)
|
| [3] |
Moens D, Hanss M. Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: Recent advances.
Finite Elements in Analysis and Design, 2011, 47(1): 4-16.
DOI:10.1016/j.finel.2010.07.010 ( 0) 0)
|
| [4] |
Wang L, Wang X J, Su H, et al. Reliability estimation of fatigue crack growth prediction via limited measured data.
International Journal of Mechanical Sciences, 2017, 121: 44-57.
DOI:10.1016/j.ijmecsci.2016.11.020 ( 0) 0)
|
| [5] |
Wang L, Wang X J, Li X. Inverse system method for dynamic loads identification via noisy measured dynamic responses.
Engineering Computations, 2016, 32(4): 1070-1094.
DOI:10.1108/EC-04-2015-0103 ( 0) 0)
|
| [6] |
Wang L, Wang X J. Dynamic loads identification in presence of unknown but bounded measurement errors.
Inverse Problems in Science & Engineering, 2015, 23(8): 1-29.
DOI:10.1080/17415977.2014.993979 ( 0) 0)
|
| [7] |
Lassen T, Sørensen J D. A probabilistic damage tolerance concept for welded joints. Part 1: data base and stochastic modelling.
Marine Structures, 2002, 15(6): 599-613.
DOI:10.1016/S0951-8339(02)00020-5 ( 0) 0)
|
| [8] |
Wang X J, Wang L. Uncertainty quantification and propagation analysis of structures based on measurement data.
Mathematical & Computer Modelling, 2011, 54(11-12): 2725-2735.
DOI:10.1016/j.mcm.2011.06.060 ( 0) 0)
|
| [9] |
Wang C, Qiu Z P, He Y Y. Fuzzy stochastic finite element method for the hybrid uncertain temperature field prediction.
International Journal of Heat & Mass Transfer, 2015, 91: 512-519.
DOI:10.1016/j.ijheatmasstransfer.2015.08.003 ( 0) 0)
|
| [10] |
Wang C, Qiu Z P. Uncertain temperature field prediction of heat conduction problem with fuzzy parameters.
International Journal of Heat & Mass Transfer, 2015, 91: 725-733.
DOI:10.1016/j.ijheatmasstransfer.2015.08.023 ( 0) 0)
|
| [11] |
Nguyen H T. A note on the extension principle for fuzzy sets.
Journal of Mathematical Analysis and Applications, 1978, 64(2): 369-380.
DOI:10.1016/0022-247X(78)90045-8 ( 0) 0)
|
| [12] |
Moore R E, Kearfott R B, Cloud M J.
Introduction to Interval Analysis. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2009.
( 0) 0)
|
| [13] |
De Boor C, Ron A. On multivariate polynomial interpolation.
Constructive Approximation, 1990, 6(3): 287-302.
DOI:10.1007/bf01890412 ( 0) 0)
|
| [14] |
Myers R H, Montgomery D C, Anderson-Cook C M.
Response Surface Methodology: Process and Product Optimization Using Designed Experiments. Hoboken, NJ: John Wiley & Sons, 2011.
( 0) 0)
|
| [15] |
Jones D R, Schonlau M, Welch W J. Efficient global optimization of expensive black-box functions.
Journal of Global Optimization, 1998, 13(4): 455-492.
DOI:10.1023/a:1008306431147 ( 0) 0)
|
| [16] |
Martin J D, Simpson T W. Use of kriging models to approximate deterministic computer models.
AIAA Journal, 2005, 43(4): 853-863.
DOI:10.2514/1.8650 ( 0) 0)
|
| [17] |
Kleijnen J P C. Kriging metamodeling in simulation: A review.
European Journal of Operational Research, 2009, 192(3): 707-716.
DOI:10.1016/j.ejor.2007.10.013 ( 0) 0)
|
| [18] |
Park J, Sandberg I W. Universal approximation using radial-basis-function networks.
Neural Computation, 1991, 3(2): 246-257.
DOI:10.1162/neco.1991.3.2.246 ( 0) 0)
|
| [19] |
Chen S, Cowan C F N, Grant P M. Orthogonal least squares learning algorithm for radial basis function networks.
IEEE Transactions on Neural Networks, 1991, 2(2): 302-309.
DOI:10.1109/72.80341 ( 0) 0)
|
| [20] |
Elanayar V T S, Shin Y C. Radial basis function neural network for approximation and estimation of nonlinear stochastic dynamic systems.
IEEE Transactions on Neural Networks, 1994, 5(4): 594-603.
DOI:10.1109/72.298229 ( 0) 0)
|
| [21] |
Klimke A, Nunes R F, Wohlmuth B I. Fuzzy arithmetic based on dimension-adaptive sparse grids: a case study of a large-scale finite element model under uncertain parameters.
International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2006, 14(5): 561-577.
DOI:10.1142/S0218488506004199 ( 0) 0)
|
| [22] |
Klimke A, Willner K, Wohlmuth B I. Uncertainty modeling using fuzzy arithmetic based on sparse grids: applications to dynamic systems.
International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2004, 12(6): 745-759.
DOI:10.1142/S0218488504003181 ( 0) 0)
|
| [23] |
Nunes R F, Klimke A, Arruda J R F. On estimating frequency response function envelopes using the spectral element method and fuzzy sets.
Journal of Sound and Vibration, 2006, 291(3-5): 986-1003.
DOI:10.1016/j.jsv.2005.07.024 ( 0) 0)
|
| [24] |
Hurty W C. Dynamic analysis of structural systems using component modes.
AIAA Journal, 1965, 3(4): 678-685.
DOI:10.2514/3.2947 ( 0) 0)
|
| [25] |
Zhou Y T, Jiang C, Han X. Interval and subinterval analysis methods of the structural analysis and their error estimations.
International Journal of Computational Methods, 2006, 3(2): 229-244.
DOI:10.1142/S0219876206000771 ( 0) 0)
|
| [26] |
Wang C, Qiu Z P. Subinterval perturbation methods for uncertain temperature field prediction with large fuzzy parameters.
International Journal of Thermal Sciences, 2016, 100: 381-390.
DOI:10.1016/j.ijthermalsci.2015.10.013 ( 0) 0)
|
| [27] |
Rao S S, Berke L. Analysis of uncertain structural systems using interval analysis.
AIAA Journal, 1997, 35(4): 727-735.
DOI:10.2514/2.164 ( 0) 0)
|
| [28] |
Rao S S, Chen L. Numerical solution of fuzzy linear equations in engineering analysis.
International Journal for Numerical Methods in Engineering, 1998, 43(3): 391-408.
DOI:10.1002/(sici)1097-0207(19981015)43:3<391::aid-nme417>3.0.co;2-j ( 0) 0)
|
| [29] |
M ller B, Graf W, Beer M. Fuzzy structural analysis using α-level optimization.
Computational Mechanics, 2000, 26(6): 547-565.
DOI:10.1007/s004660000204 ( 0) 0)
|
| [30] |
Moens D, Vandepitte D. Fuzzy finite element method for frequency response function analysis of uncertain structures.
AIAA Journal, 2002, 40(1): 126-136.
DOI:10.2514/2.1621 ( 0) 0)
|
| [31] |
Qiu Z P, Elishakoff I. Antioptimization of structures with large uncertain-but-non-random parameters via interval analysis.
Computer Methods in Applied Mechanics and Engineering, 1998, 152(3): 361-372.
DOI:10.1016/S0045-7825(96)01211-X ( 0) 0)
|
| [32] |
Qiu Z P, Zheng Y N. Predicting fatigue crack growth evolution via perturbation series expansion method based on the generalized multinomial theorem.
Theoretical and Applied Fracture Mechanics, 2016, 86: 361-369.
DOI:10.1016/j.tafmec.2016.09.009 ( 0) 0)
|
| [33] |
McWilliam S. Anti-optimisation of uncertain structures using interval analysis.
Computers & Structures, 2001, 79(4): 421-430.
DOI:10.1016/S0045-7949(00)00143-7 ( 0) 0)
|
| [34] |
Xia B Z, Yu D J, Liu J. Interval and subinterval perturbation methods for a structural-acoustic system with interval parameters.
Journal of Fluids and Structures, 2013, 38: 146-163.
DOI:10.1016/j.jfluidstructs.2012.12.003 ( 0) 0)
|
| [35] |
Wang C, Qiu Z P, Wang X J, et al. Interval finite element analysis and reliability-based optimization of coupled structural-acoustic system with uncertain parameters.
Finite Elements in Analysis and Design, 2014, 91: 108-114.
DOI:10.1016/j.finel.2014.07.014 ( 0) 0)
|
| [36] |
Wang C, Qiu Z P, He Y Y. Fuzzy interval perturbation method for uncertain heat conduction problem with interval and fuzzy parameters.
International Journal for Numerical Methods in Engineering, 2015, 104(5): 330-346.
DOI:10.1002/nme.4932 ( 0) 0)
|
| [37] |
Wang C, Qiu Z P. Modified perturbation method for eigenvalues of structure with interval parameters.
Science China Physics, Mechanics & Astronomy, 2015, 58(1): 1-9.
DOI:10.1007/s11433-013-5328-6 ( 0) 0)
|
| [38] |
Dong W, Shah H C. Vertex method for computing functions of fuzzy variables.
Fuzzy Sets and Systems, 1987, 24(1): 65-78.
DOI:10.1016/0165-0114(87)90114-X ( 0) 0)
|
| [39] |
Rao S, Sawyer J P. Fuzzy finite element approach for analysis of imprecisely defined systems.
AIAA Journal, 1995, 33(12): 2364-2370.
DOI:10.2514/3.12910 ( 0) 0)
|
| [40] |
Chen L, Rao S S. Fuzzy finite-element approach for the vibration analysis of imprecisely-defined systems.
Finite Elements in Analysis and Design, 1997, 27(1): 69-83.
DOI:10.1016/S0168-874X(97)00005-X ( 0) 0)
|
| [41] |
Akpan U O, Koko T S, Orisamolu I R, et al. Practical fuzzy finite element analysis of structures.
Finite Elements in Analysis and Design, 2001, 38(2): 93-111.
DOI:10.1016/S0168-874X(01)00052-X ( 0) 0)
|
| [42] |
Qiu Z P, Wang X J, Chen J Y. Exact bounds for the static response set of structures with uncertain-but-bounded parameters.
International Journal of Solids and Structures, 2006, 43(21): 6574-6593.
DOI:10.1016/j.ijsolstr.2006.01.012 ( 0) 0)
|
| [43] |
Qiu Z P, Xia Y Y, Yang J L. The static displacement and the stress analysis of structures with bounded uncertainties using the vertex solution theorem.
Computer Methods in Applied Mechanics and Engineering, 2007, 196(49-52): 4965-4984.
DOI:10.1016/j.cma.2007.06.022 ( 0) 0)
|
| [44] |
Xu M H, Qiu Z P, Wang X J. Uncertainty propagation in SEA for structural-acoustic coupled systems with non-deterministic parameters.
Journal of Sound and Vibration, 2014, 333(17): 3949-3965.
DOI:10.1016/j.jsv.2014.03.003 ( 0) 0)
|
| [45] |
De Gersem H, Moens D, Desmet W, et al. Interval and fuzzy dynamic analysis of finite element models with superelements.
Computers & Structures, 2007, 85(5-6): 304-319.
DOI:10.1016/j.compstruc.2006.10.011 ( 0) 0)
|
| [46] |
Hanss M. The transformation method for the simulation and analysis of systems with uncertain parameters.
Fuzzy Sets and Systems, 2002, 130(3): 277-289.
DOI:10.1016/S0165-0114(02)00045-3 ( 0) 0)
|
| [47] |
Hanss M. The extended transformation method for the simulation and analysis of fuzzy-parameterized models.
International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2003, 11(6): 711-727.
DOI:10.1142/S0218488503002491 ( 0) 0)
|
| [48] |
Hanss M, Turrin S. A fuzzy-based approach to comprehensive modeling and analysis of systems with epistemic uncertainties.
Structural Safety, 2010, 32(6): 433-441.
DOI:10.1016/j.strusafe.2010.06.003 ( 0) 0)
|
| [49] |
Junge M, Brunner D, Becker J, et al. Combination of fuzzy arithmetic and a fast boundary element method for acoustic simulation with uncertainties.
Journal of Computational Acoustics, 2009, 17(1): 45-69.
DOI:10.1142/S0218396X09003811 ( 0) 0)
|
| [50] |
Allahviranloo T, Kiani N A, Motamedi N. Solving fuzzy differential equations by differential transformation method.
Information Sciences, 2009, 179(7): 956-966.
DOI:10.1016/j.ins.2008.11.016 ( 0) 0)
|
| [51] |
Gauger U, Turrin S, Hanss M, et al. A new uncertainty analysis for the transformation method.
Fuzzy Sets and Systems, 2008, 159(11): 1273-1291.
DOI:10.1016/j.fss.2007.12.027 ( 0) 0)
|
| [52] |
Massa F, Tison T, Lallemand B. A fuzzy procedure for the static design of imprecise structures.
Computer Methods in Applied Mechanics and Engineering, 2006, 195(9-12): 925-941.
DOI:10.1016/j.cma.2005.02.015 ( 0) 0)
|
| [53] |
Giannini O, Hanss M. The component mode transformation method: A fast implementation of fuzzy arithmetic for uncertainty management in structural dynamics.
Journal of Sound and Vibration, 2008, 311(3-5): 1340-1357.
DOI:10.1016/j.jsv.2007.10.029 ( 0) 0)
|
| [54] |
Moens D, Vandepitte D. An interval finite element approach for the calculation of envelope frequency response functions.
International Journal for Numerical Methods in Engineering, 2004, 61(14): 2480-2507.
DOI:10.1002/nme.1159 ( 0) 0)
|
| [55] |
Xia B Z, Yu D J. Modified sub-interval perturbation finite element method for 2D acoustic field prediction with large uncertain-but-bounded parameters.
Journal of Sound and Vibration, 2012, 331(16): 3774-3790.
DOI:10.1016/j.jsv.2012.03.024 ( 0) 0)
|
| [56] |
Wang C, Qiu Z P, Li Y L. Hybrid uncertainty propagation of coupled structural-acoustic system with large fuzzy and interval parameters.
Applied Acoustics, 2016, 102: 62-70.
DOI:10.1016/j.apacoust.2015.09.006 ( 0) 0)
|
| [57] |
De Gersem H, Moens D, Desmet W, et al. A fuzzy finite element procedure for the calculation of uncertain frequency response functions of damped structures: Part 2-Numerical case studies.
Journal of Sound and Vibration, 2005, 288(3): 463-486.
DOI:10.1016/j.jsv.2005.07.002 ( 0) 0)
|
| [58] |
Moens D, Vandepitte D. A fuzzy finite element procedure for the calculation of uncertain frequency-response functions of damped structures: Part 1-Procedure.
Journal of Sound and Vibration, 2005, 288(3): 431-462.
DOI:10.1016/j.jsv.2005.07.001 ( 0) 0)
|
| [59] |
Farkas L, Moens D, de Gersem H, et al. Efficient FE reanalysis method for fuzzy uncertainty analysis of a composite wing. Proceedings of the 10th AIAA Non-Deterministic Approaches Conference.
Schaumburg, 2008: 1-11.
DOI:10.2514/6.2008-2296 ( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


