2. School of Automation, Beijing University of Posts and Telecommunications, Beijing 100876, China
Due to the inevitable manufacturing and assembly tolerance, normally robot's actual kinematic model deviates slightly from the theoretical model. As a result, the errors from the deviation of two robot kinematic models would directly result in the pose and trajectory inaccuracy if the nominal model was used to calculate the robot's pose[1]. In order to enhance positioning accuracy, as an economical and efficient way, robot calibration is usually used to obtain the actual kinematic parameters.
The robot's absolute positioning accuracy is mainly influenced by three aspects, such as kinematic parameters, pose of the base frame and tool center point (TCP). Hayati and Judd's MDH model[2-5], Veitschegger and Wu's model[6], Driels's another modified DH model[7], Stone and Sanderson's S-model[8], Zhuang's complete and parametrically continuous (CPC) model[9], Sheth's shape matrix model[10] and product-of-exponential (POE) model[1, 11-13] are widely used for kinematic calibration. In general, the robot kinematics model is described relative to the base frame, which is one of important prerequisites of the kinematics parameters identification and error compensation[14-15]. Therefore, it is necessary of exact modeling and analysis of base coordinate frame. However, the research on this field is limited. Zhang et al.[16] proposed a linear method and a modified particle swarm optimization theory to calibrate ABF by means of dealing with a typical hand-eye problem through some simulations. The calibration result can be acquired by combining the kinematics and the end-effector's 3D position provided by the camera. Aiming at the calibration of robot's ABF, Zhang et al.[17] presented a geometric method combining single axis rotation and tool data of the robot measured by a laser tracker in real-time. In the calibration system, circular locus generated from the robot single axis rotation is spatial circle fitted, then the unit normal vector is obtained and the rotation matrix is calculated, and at last the translation vector can be obtained due to the rotation matrix. Gan et al.[18] presented an ABF calibration method for multi-robot system. In this method, a series of "handclasp" manipulations were taught between two coordinated robots within the robot workspace and used the contact point's relevant position information, and it realized ABF calibration by an optimal estimation. Qi et al.[19]developed a novel method for calibrating the ABF automatically which was a pose matrix between the robot's ABF and external measuring equipment by means of distance restriction and fractional steps according to the character of industrial robot's position error measuring system composed of a 6-DOF robot and a laser tracker. Wang et al.[20] proposed a two-step accurate calibration method using quaternion form to solve the problem of ABF calibration. Based on forward kinematics and 3D positions collected from external measurement, the orthogonality calibration result could be obtained by using the geometrical constraints of a quaternion. Wu et al.[21] found a mathematics model of robot's ABF calibration by solving a hand-eye calibration problem in the LBR iiwa14 R820 platform. The transformation relation can be acquired by using the 3D position only provided by the camera mounted at the end of the robot.
In practice, mechanical errors usually lead to the fact that the ABF does not coincide with the NBF used by the robot controller. In this paper, in order to calibrate the transformation relation between the ABF and the NBF, a new approach is to be discussed, which uses only a series of robot end-effector's 3D position obtained by precision measuring device and its corresponding joint angles.
2 Base Frame Calibration Model 2.1 Forward Kinematics Using POEThe forward kinematics of a serial robot based on Product of Exponentials Formula (POE) formula was initially described by Brockett[8]. As all joint twists are related to the inertial frame, so it only requires two coordinate frames to be attached, which are the base frame {S} and tool coordinate frame {T}, the former is intuitively attached to the robot's base link, while the latter is attached to the end-effector. We can use gst(0) to represent the transformation from {S} to {T} when robot is in its reference configuration, with all joint angles q={0}. The
Based on the POE formula, the generic forward kinematics for a serial robot with n-DOF is given by:
| $ \begin{array}{l} {g_{st}} = \exp \left( {\mathop {{\xi _1}}\limits^ \wedge {q_1}} \right) \cdots \exp \left( {\mathop {{\xi _n}}\limits^ \wedge {q_n}} \right){g_{st}}\left( 0 \right) = \\ \;\;\;\;\;\prod\limits_{i = 1}^n {\exp \left( {\mathop {{\xi _i}}\limits^ \wedge {q_i}} \right){g_{st}}\left( 0 \right)} \end{array} $ | (1) |
However, the actual base coordinate frame {S'} is difficult to coincide with the nominal one {S}. There is a transformation gs's between {S'} and {S}. Therefore, gs't(q) can be expressed as:
| $ {g_{s't}}\left( \mathit{\boldsymbol{q}} \right) = {g_{s's}}{g_{st}}\left( \mathit{\boldsymbol{q}} \right) = {g_{s's}}\prod\limits_{i = 1}^n {\exp \left( {\mathop {{\xi _i}}\limits^ \wedge {\mathit{\boldsymbol{q}}_i}} \right){g_{st}}\left( 0 \right)} $ | (2) |
Assume that the transformation of {T} with respect to {S'} is expressed as the format gs't(q)=
| $ {\mathit{\boldsymbol{P}}_{s't}} = {\mathit{\boldsymbol{R}}_{s's}}{\mathit{\boldsymbol{P}}_{st}} + {\mathit{\boldsymbol{P}}_{s's}} $ | (3) |
Denote f(Rs's, Ps's)=Ps't-Rs'sPst-Ps's, the ABF calibration problem can be abstracted to minimum optimization problem, which is essentially to calculate a 3×3 rotation matrix Rs's and a 3×1 translation vector Ps's, so that:
| $ \min \sum\limits_{j = 1}^m {{{\left\| {{f_j}} \right\|}^2}} $ | (4) |
where j and m indicate the sequential and the total measurement number, respectively.
2.2 Orthogonal Modified Algorithm of Procrustes AnalysisTheoretically, the rotation matrix must be orthogonal and normalized in Cartesian coordinate system. In order to satisfy the above condition, Procrustes Analysis[22-23]is introduced to optimize the rotation matrix. In mathematics, Procrustes Analysis solution to the problem of base frame calibration is essentially to calculate the matrix R, which is obtained by minimizing the function min║AR-B║F.In the minimizing problem, matrix A and B are known, and ║●║F is the Frobenius norm. Define the set of orthogonal matrices as orthogonal Stiefel manifolds: S={R∈R3×3:RTR=I}, subject to det(R)=1.
Considering the orthonormal constraints of the rotation matrix, the calibration model can be considered as an equilibrium problem. Therefore, the constrained orthogonal Procrustes Analysis problem can be described as:
| $ \left\{ \begin{array}{l} \min {\left\| {\mathit{\boldsymbol{AR}} - \mathit{\boldsymbol{B}}} \right\|_F},\mathit{\boldsymbol{A}} \in {{\bf{R}}^{3 \times 3}},\mathit{\boldsymbol{B}} \in {\mathit{\boldsymbol{R}}^{3 \times 3}}\\ {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}} = \mathit{\boldsymbol{I}} \end{array} \right. $ | (5) |
In order to solve Eq.(5), the Lagrangian function is established :
| $ \begin{array}{l} f\left( \mathit{\boldsymbol{R}} \right) = \mathop {\min }\limits_{{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}} = \mathit{\boldsymbol{I}}} \left\| {\mathit{\boldsymbol{AR}} - \mathit{\boldsymbol{B}}} \right\|_F^2 + \mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}} - \mathit{\boldsymbol{I}}} \right) = \\ \;\;\;\;\;{\rm{tr}}{\left( {\mathit{\boldsymbol{AR}} - \mathit{\boldsymbol{B}}} \right)^{\rm{T}}}\left( {\mathit{\boldsymbol{AR}} - \mathit{\boldsymbol{B}}} \right) + {\rm{tr}}\left[ {\mathit{\boldsymbol{K}}\left( {{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}} - \mathit{\boldsymbol{I}}} \right)} \right] \end{array} $ | (6) |
where K is the matrix (unknown) of Lagrange multipliers.
The optimal matrix can be performed by setting the derivative of f(R) to zero, we can get:
| $ \frac{{\partial f\left( \mathit{\boldsymbol{R}} \right)}}{{\partial \mathit{\boldsymbol{R}}}} = 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AR}} - 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{K}} + {\mathit{\boldsymbol{K}}^{\rm{T}}}} \right) = 0 $ | (7) |
For clearness, we denote M=ATA, N=ATB, C=(K+K)T/2. Hence one has to solve:
| $ \mathit{\boldsymbol{MR}} - \mathit{\boldsymbol{N}} + \mathit{\boldsymbol{RC}} = 0 $ | (8) |
Let us multiply Eq.(8) on the left by RT:
| $ {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{MR}} - {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{N}} + {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{RC}} = 0 $ | (9) |
As matrices RTMR and C are symmetric, we can deduce matrix RTN is also symmetric. Therefore, matrix RTN satisfies the following properties:
| $ {\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{R}} $ | (10) |
Eq.(10) is equivalent to:
| $ \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^{\rm{T}}} = \mathit{\boldsymbol{R}}{\mathit{\boldsymbol{N}}^{\rm{T}}}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{R}}^{\rm{T}}} $ | (11) |
Matrices N can be obtained using SVD:
| $ \mathit{\boldsymbol{N}} = \mathit{\boldsymbol{UD}}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (12) |
where U, V are orthonormal matrices. Then plugging U and V into Eq.(11), we can get
| $ \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{D}}^2}{\mathit{\boldsymbol{U}}^{\rm{T}}} = \mathit{\boldsymbol{RV}}{\mathit{\boldsymbol{D}}^2}{\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{R}}^{\rm{T}}} $ | (13) |
From Eq.(13), we obtain U=RV, and finally we get:
| $ \mathit{\boldsymbol{R}} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (14) |
Similarly, for solving of equation min║RA-B║F, where N=ABT, we can use SVD to get the solution of min║RA-B║F.
From Eq. (14) we can get rotation matrix R, by plugging Eq.(14) into Eq.(3), then the translation vector can be obtained.
| $ {\mathit{\boldsymbol{P}}_{s's}} = \sum\limits_{j = 1}^m {\frac{{{\mathit{\boldsymbol{P}}_{s't}}}}{m}} - \mathit{\boldsymbol{R}}\sum\limits_{i = 1}^m {\frac{{{\mathit{\boldsymbol{P}}_{st}}}}{m}} $ | (15) |
A real-world experiment has been conducted to verify the accuracy and usefulness of the ABF calibration method. The setup consists of an industrial 6-DOF serial robot, a FARO laser tracker and a spherical target ball.
The structure characteristic of the 6-DOF serial manipulators is as follows: the first three joints are nonintersecting, of which the second and third joint axes are parallel and different planes from the first joint axis, the other fourth, fifth, sixth joint axes are intersected at one point, and all of them meet the Pieper criteria. Applying the method of Screw Theory to establish each joint coordinate system is as shown in Fig. 1, and the corresponding kinematic parameters are shown in Table 1.

|
Figure 1 Forward kinematics of a 6-DOF serial robot |
| Table 1 Kinematic parameters of the 6-DOF serial robot |
The target ball with a diameter of 38.1 mm is utilized to construct {T}, whose center relative to the wrist position offsets is -6.55 mm, 6.732 mm, 290.95 mm. When the distance from laser tracker to robot is less than 10 m, the theoretical measurement accuracy of the laser tracker is about 0.022 mm, which satisfies the experimental requirement.
3.2 Procedure of Base Frame Calibration and Data AcquisitionFig. 2 shows the experimental setup. In order to improve and maintain the measurement accuracy, a FARO laser tracker is mainly used in this procedure to measure the 3D position of the target ball. According to the actual working requirement, by teaching the robot in its working space, the Z' and X'-coordinate axis of the ABF can be established through the software of laser tracker. At last, according to the right-hand rule

|
Figure 2 Experiment setup with a 6-DOF robot and a FARO laser tracker |
In the data acquisition processing, when the ABF is calibrated, then all the 3D position measuring data should be mapped from FARO laser tracker coordinates to the actual base coordinates. Because of the limit of the measurement range of the laser tracker, 30 poses are randomly generated within the workplace of the robot, in which the first 15 are used for calibration and the last 15 for validation. A series of robot joint angles (q1, q2, q3, q4, q5, q6) of the robot motion read from robot controller and the target ball position (px, py, pz) read from the software of laser tracker are given in Table 2.
| Table 2 Robot joint configurations and positions of target ball |
3.3 Identification Procedure
To obtain the homogeneous transformations between the two base frames, the overall solution procedure is as follows: Eq.(1) is used to compute the vector Pst using the POE formulation. Ps't is obtained from the measuring data of laser track. Eq.(14) is used to compute the matrix Rs's while Ps's obtained from Eq.(15) with the unit of mm. Without considering the error of robot kinematics parameters, the homogeneous transformation from {S} to {S'} can be obtained.
| $ \begin{array}{l} {\mathit{\boldsymbol{g}}_{s's}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{s's}}}&{{\mathit{\boldsymbol{P}}_{s's}}}\\ 0&1 \end{array}} \right] = \\ \;\;\;\;\;\;\left[ {\begin{array}{*{20}{r}} {1.000\;0}&{0.000\;3}&{0.000\;4}&{0.901\;4}\\ { - 0.000\;3}&{1.000\;0}&{0.000\;3}&{ - 0.201\;0}\\ { - 0.000\;4}&{ - 0.000\;3}&{1.000\;0}&{0.891\;8}\\ 0\;&0\;&0\;&{0.100\;0} \end{array}} \right] \end{array} $ |
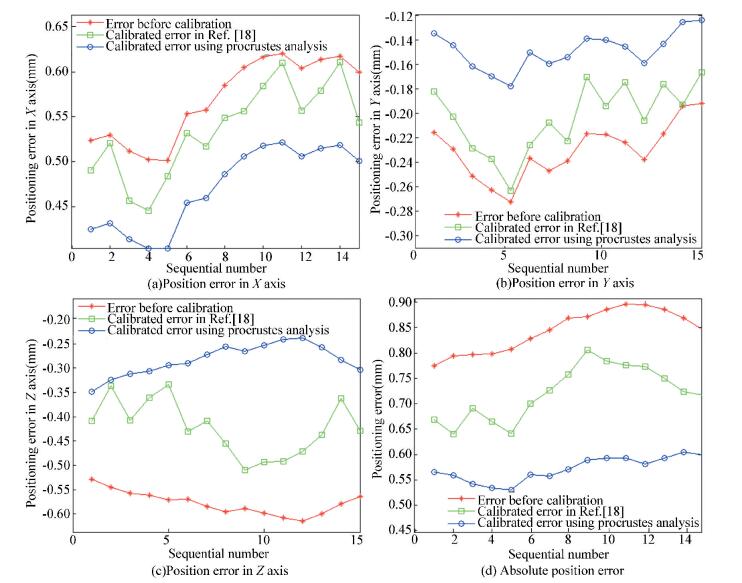
Finally, now we use the last 15 poses from the Table 2 to validate the correctness of the calibrated value. The deviation of the end-effector's actual and nominal position coordinates is defined as the absolute positioning error. In comparison with other calibration method in Ref.[18], the calibration result is shown in Fig. 3, where Figs. 3(a)-(d) represent positioning error in X, Y, Z axis direction and absolute positioning error respectively.
|
Figure 3 Comparison of calibration results |
The comparative analysis of positioning error results show that both single direction precision and absolute precision have been improved after calibration by the method proposed in Ref.[18] and Procrustes Analysis compared with before calibration. Corresponding to the two methods, average positioning errors of single direction in X, Y, Z axis direction decrease from 0.569 mm to 0.543 mm and 0.471 mm, from -0.230 mm to -0.212 mm and -0.149 mm, from -0.578 mm to -0.423 mm and -0.283 mm, respectively, and maximum errors of them decrease accordingly. By the method in Ref.[18], absolute positioning error at point 9 is the greatest, and the error can reach 0.807 mm, the error at point 2 is the minimum with error 0.640 mm, and its average error is 0.721 mm. While absolute positioning error using Procrustes Analysis at point 14 reach the greatest with error 0.605 mm, while at point 5 is the minimum with error 0.530 mm, its average error decreases from 0.844 mm to 0.572 mm. Hence the proposed Procrustes Analysis can greatly decrease both average error and maximum error. Meanwhile, we can learn that error distribution is more evenly than before calibration and the method in Ref.[18] influenced by the orthogonality of the rotation matrix. As Procrustes Analysis algorithm has the advantage in dealing with orthogonality of the matrix, it is easier for us to get the optimal solution.
4 ConclusionsBased on the POE formulation and using Procrustes Analysis, a novel effective approach has been proposed in this paper to calibrate the ABF of serial robot caused by mechanical manufacturing errors only using 3D position.
1) Using the theory of Procrustes Analysis, the proposed calibration model has not only proven to be effective in calibrating 6-DOF serial manipulators but it is also favored from a computational efficiency viewpoint since it ensures the orthonormal constraints of rotation matrix as well as the precise solutions.
2) The method of calibrating the actual base coordinate frame can also be suitable for any serial robot. The superiority of this method lies in its easy operational step and simple calibrating environment.
3) The developed approach is implemented to 6-DOF serial robot and its resulting improvement of the positioning accuracy is addressed, which lays the foundation for robot off-line programming. To improve the absolute precision even more, kinematics calibration is also essential.
4) Theoretically, the calibration method for solving the transformation relation provides a reference for other same problems, such as multi-robot coordination and robot hand-eye system calibration.
| [1] |
He Ruibo, Zhao Yingjun, Yang Shunian, et al. Kinematic-parameter identification for serial-robot calibration based on POE formula. IEEE Transactions on Robotics, 2010, 26(3): 411-423. DOI:10.1109/TRO.2010.2047529 ( 0) 0)
|
| [2] |
Hayati S A. Robot arm geometric link parameter estimation. Proceedings of the 22nd IEEE Conference on Decision and Control. Piscataway:IEEE, 1983, 12(22): 1477-1483. DOI:10.1109/CDC.1983.269783 ( 0) 0)
|
| [3] |
Hayati S A, Mirmirani M. Improving the absolute positioning accuracy of robot manipulators. Journal of Robotic Systems, 1985, 2(4): 397-413. DOI:10.1002/rob.4620020406 ( 0) 0)
|
| [4] |
Hayati S A, Tso K, Roston G. Robot geometry calibration. Robotics and Automation, 1988, 4: 947-951. ( 0) 0)
|
| [5] |
Judd R P, Knasindki A B. A technique to calibrate industrial robots with experimental verification. IEEE Transaction on Robotics and Automation, 1990, 6(1): 20-30. DOI:10.1109/70.88114 ( 0) 0)
|
| [6] |
Veitschegger W, Wu C H. Robot accuracy analysis based on kinematics. Robotics and Automation, 1986, 2(3): 171-180. ( 0) 0)
|
| [7] |
Driels M R, Pathre U S. Robot manipuilator kinematic compensation using a generalized Jacobian formulation. Journal of Robotic System, 1987, 4(2): 259-280. DOI:10.1002/rob.4620040208 ( 0) 0)
|
| [8] |
Stone H, Sanderson W. A prototype arm signature identification system. Proceedings of the IEEE International Conference on Robotics and Automation. Piscataway:IEEE, 1987, 4: 175-182. DOI:10.1109/ROBOT.1987.1087835 ( 0) 0)
|
| [9] |
Zhuang H, Roth Z S, Hamano F. A complete and parametrically continuous kinematic model for robot manipulators. IEEE Transactions on Robotics and Automation, 1992, 8(4): 451-463. DOI:10.1109/70.149944 ( 0) 0)
|
| [10] |
Sheth P N, Uicker J J. IMP (Integrated Mechanisms Program), a computer aided design analysis system for mechanisms and linkages. Journal of Engineering for Industry, 1972, 94(2): 454-464. DOI:10.1115/1.3428176 ( 0) 0)
|
| [11] |
Brockett R W. Robotic manipulators and the product of exponentials formula. Mathematical Theory of Networks and Systems, 1984, 120-129. DOI:10.1007/BFb0031048 ( 0) 0)
|
| [12] |
Okamura K, Park F. Kinematic calibration using the product of exponentials formula. Robotica, 1996, 14(4): 415-421. DOI:10.1017/S0263574700019810 ( 0) 0)
|
| [13] |
He Ruibo, Li Wenxin, Shi Tujin, et al. A kinematic calibration method based on the product of exponentials formula for serial robot using position measurements. Robotica, 2014, 33(6): 1-19. DOI:10.1017/S026357471400071X ( 0) 0)
|
| [14] |
Du Liang, Shi Guangming, Guan Weibin, et al. Compensation of kinematic geometric parameters error and comparative study of accuracy testing for robot. Proceedings of the SPIE 9297, International Symposium on Optoelectronic Technology and Application 2014: Laser and Optical Measurement Technology; and Fiber Optic Sensors. Bellingham, 2014, 9297(1/2): 1-13. DOI:10.1117/12.2073187 ( 0) 0)
|
| [15] |
Zhang Tie, Du Liang, Dai Xianliang. Test of robot distance error and compensation of kinematic full parameters. Advances in Mechanical Engineering, 2014, 6: 1-9. DOI:10.1155/2014/810684 ( 0) 0)
|
| [16] |
Zhang Xu, Li Aiguo, Ma Zi, et al. Simultaneous calibration for relationship of robot hand-eye, base coordinates and world coordinates. Control and Decision, 2009, 24(10): 1532-1539. ( 0) 0)
|
| [17] |
Zhang Bo, Wei Zhenzhong, Zhang Guangjun. Rapid coordinate transformation between a robot and a laser tracker. Chinese Journal of Scientific Instrument, 2010, 31(9): 1986-1990. ( 0) 0)
|
| [18] |
Gan Yanhui, Dai Xianzhong. Base frame calibration for coordinated industrial robots. Robotics and Autonomous Systems, 2011, 59(7/8): 563-570. DOI:10.1016/j.robot.2011.04.003 ( 0) 0)
|
| [19] |
Qi Lizhe, Chen Lei, Wang Wei, et al. The calibration for industrial robot's position error measuring system based on the laser tracker. Manufacturing Technology and Machine Tool, 2012, 107(5): 206-211. ( 0) 0)
|
| [20] |
Wang Wei, Liu Fei, Yun Chao. Calibration method of robot base frame using unit quaternion form. Precision Engineering, 2015, 41(3): 47-54. DOI:10.1016/j.precisioneng.2015.01.005 ( 0) 0)
|
| [21] |
Liao Wu, Ren Hongliang. Finding the kinematic base frame of a robot by hand-eye calibration using 3D position data. IEEE Transactions on Automation Science and Engineering, 2016, 14(1): 314-324. DOI:10.1109/TASE.2016.2517674 ( 0) 0)
|
| [22] |
Peter H S. A generalized solution of the orthogonal Procrustes problem. Psychometrika, 1966, 31(1): 1-10. DOI:10.1007/BF02289451 ( 0) 0)
|
| [23] |
Du Keqin. Researches on Procrustes problems. Hangzhou: Zhejiang University, 2005. (in Chinese)
http: //cdmd. cnki. com. cn/Article/CDMD-10335-2006120006. htm
( 0) 0)
|
 2017, Vol. 24
2017, Vol. 24


