2. School of Electrical and Information Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China;
3. Beijing Key Laboratory for Research on Intelligent Processing Method of Building Big Data(Beijing University of Civil Engineering and Architecture), Beijing 100044, China;
4. Institute of Materials, China Academy of Engineering Physics, Mianyang 621700, Sichuan, China
MICRORNAs (miRNAs) are a class of small endogenous non-coding RNA, and they cause translational repression or target degradation by binding to the complementary sites in the 3' UTR of target genes[1]. MiRNAs are considered to represent one of the most important components of biological process, and increasing evidence has revealed that miRNAs play an important role in tissue development, cell growth, cellular signaling, and so on[2-3]. It has been reported that about one third of human genes can be regulated by miRNAs[4-5]. Thus, the dysfunction of miRNA and the dysregulation of target genes can affect cell biological behavior, and ultimately lead to various diseases such as diabetes[6], neurodegenerative disease[7], and so on. So far, 35828 miRNAs in 223 species have been reported in miRBase (Release 21)[8]. However, the current knowledge about miRNA target mechanism and miRNA function are rarely known, especially the available knowledge about the disease-miRNA associations. Because the experiments identification of miRNA-disease associations by current genomic techniques is costly and time consuming, therefore, it is increasingly necessary to develop powerful computational methods that used to detect potential disease-related miRNAs.
At present, many computational methods about miRNA-disease association prediction have been proposed. Most of them are based on traditional network similarity measures. The network similarity measure starts with constructing an association network based on miRNA and phenotype information, and then each candidate is scored according to the known disease related miRNAs. The high-scoring candidates are believed to be involved in the regulation of certain disease. For instance, Jiang et al.[9] devised a scoring system, and they used the neighbor information of each miRNA in the functional interactions network to evaluate the degree of a miRNA involved in the disease, they believed that a high-scoring miRNA was likely to be involved in the disease. Chen[10] adopted global network similarity measure and inferred latent disease-associated miRNAs from similarity network using random walk algorithm. Chen[11] presented three methods to predict disease-associated miRNAs named MBSI (microRNA-based similarity inference), PBSI (phenotype-based similarity inference) and NetCBI (network-consistency-based inference) using global network similarity measure as well. This kind of network similarity measure methods established associations from miRNA to disease directly. However, the emergence of disease is a complicated process resulting from interactions among various biomolecules. Thus, there are no direct causal relation existing between miRNAs and diseases. Herein, researchers try to integrate a variety of intermediary biomolecules to study miRNA-disease associations indirectly. Soren Mork[12] regarded protein as the mediators and predicted miRNA-disease associations by coupling the network analysis of miRNA-protein associations with the text mining of protein-disease associations, they ranked the strength of miRNA-disease associations by the inference of two scores. Zhang[13] identified potential disease associated miRNAs by integrating diseasegene association, clusters, family analysis and Gene Ontology data. However, (1) until now, none of these methods can define the threshold exactly, leading to a lot of false positive and false negative results, (2) the biological knowledge used by the methods of network similarity measure are limited, leading to the bottleneck of this kind of methods, (3) each type of cancer has various distinctive subtypes and the progression of each tumor subtype corresponds to different phenotypes (e.g. metastasis, resistance to certain treatment, et al.), and each of these phenotypes can correlate to a certain group of miRNAs. Simply looking for "cancer-associated miRNAs" is not that helpful for understanding and especially treatment of the specific process of disease.
Many studies showed that miRNAs are significant indicators for specific diseases and can be used to differentiate cancer types solely by miRNA expression profiling[14-17]. Meanwhile, some researches demonstrated that miRNA expression profiling-based classification is efficient at identifying the tissue of poorly differentiated cancers[15, 18]. Furthermore, inference of disease-miRNA associations from expression profiling is particularly attractive because it allows the discovery of tissue specificity and temporal specificity of miRNA-disease association. Thus, with the increasing number of available high-throughput biological data, the miRNA expression profiling-based approaches for identifying disease-miRNA associations should be proposed.
We predict disease-miRNA associations lifting the limitation of poor knowledge of miRNAs function and gene ontology by using miRNA expression data. In the first step, the reliable training dataset is constructed by combining the advantages of both direct and indirect disease-miRNA association prediction methods and the superiority of step has been validated. In the second step, to predict spatial and temporal-specific disease-associated miRNAs, Hidden Conditional Random Field (HCRF) is applied to three human miRNAs expression datasets which are GSE68951, GSE58606 and GSE41655. Finally, the 5-fold cross validation is applied to validate the performance of this method, and the results show that the proposed method achieves superior performance on 3 human diseases with AUC values of 0.656 8, 0.727 2, and 0.699 3, respectively.
2 Methods 2.1 Data Retrieval and Pre-processAt first, the miRNA expression profiling in subtypes of lung carcinomas, breast cancer and colorectal cancer are downloaded from Gene Expression Omnibus (GEO; http://www.ncbi.nlm.nih.gov/geo) with the series ac-cession number GSE68951, GSE58606, and GSE41655, respectively. There are 1205 miRNAs with 215 samples in GSE68951, 1926 miRNAs with 134 samples in GSE58606 and 851 miRNAs with 111 samples in GSE41655 retained after preprocess. Furthermore, experimentally validated miRNA-target pairs are downloaded from miRecord[19] based on these miRNAs. The miRNA-miRNA functional similarity scores which are the supplementary material along with literature[10] are downloaded as well. After that, the disease-gene association are acquired from DISEASES[20] (http://diseases.jensenlab.org) which is a web resource that integrates evidence on disease-gene associations. At last, the miRNA-disease association data are obtained from human miRNA-associated disease database (HMDD, http://210.73.221.6/hmdd)[2, 21] which collects 10368 entries that include 572 miRNA genes, 378 diseases from 3 511 papers currently. In this study, we investigate the associations between miRNAs and human lung cancer, human breast cancer and human colorectal cancer, respectively. Finally, 408 candidate miRNAs for human lung cancer, 806 candidate miRNAs for human breast cancer and 366 candidate miRNAs for human colorectal cancer are selected. Furthermore, the corresponding Gene Ontology (GO)[22] data are obtained.
2.2 Construction of Reliable Training DatasetSo far, for the prediction methods of miRNA-disease association, the two main concerns are direct miRNA-disease association and indirect miRNA-gene-disease association. However, none of them is strictly outperforming the others under the condition that miRNA function and target mechanism are still poorly understood. Furthermore, there seems to be a poor agreement between the results of different algorithms because these algorithms rely on different kinds of biological data in making prediction, each of which has its own advantages. Therefore, we consider two kinds of algorithms and try to take advantage of two algorithms in order to assign reliable class label for each miRNA in training data.
The class label for each candidate miRNA is assigned according to the following two steps. In the first step, miRNA-disease associations are predicted by two kinds of methods separately, and the algorithms provide corresponding predicted score for each miRNA, respectively. In the second step, a decision fusion method is used to aggregate the results provided by the algorithms according to their capabilities.
2.2.1 Calculation of direct miRNA-disease associationIt is reported that miRNAs with similar functions are often associated with similar functions and associated with similar diseases. Many studies examined functional similarity of two miRNAs by measuring the semantic similarity of their associated diseases[10, 23-24]. In this step, the miRNA-disease associations are calculated according to Chen's method[10]. We first download the relevant data according to Section 2.1 and construct a miRNA-disease association network shown as "Direct computation" in Fig. 1. In this network, Two vertices sets M={m1, m2, …, mn} and D={d1, d2, …, dk} represents the set of n miRNAs and k diseases, respectively. Vertex mi and dj are linked by an edge in this association network if miRNA i is associated with disease j in the dataset, where 1≤i≤n, 1≤j≤k. The weight of edges between mi and dj are set to 1. In the first step, direct and indirect computations are performed. In the second step, the corresponding miRNAs are prioritized. In the third step, the decision fusion method is applied to combine the advantages of direct and indirect methods.
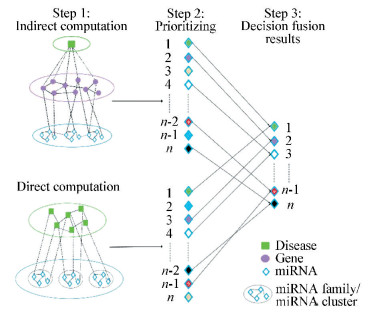
|
Figure 1 Sketch of decision fusion process |
Any two miRNA vertexes are connected by the line if the functional similarity score is greater than "0" and the weight of edges between two miRNAs are set to the score. All of the miRNAs in this study are divided into two groups, and the known disease-associated miRNAs are assigned to seed group while the other miRNAs are assigned to candidate group. The initial probability p(0) is assigned to each seed miRNA equally, t and the sum of these initial probabilities is 1. While the initial probability of candidate miRNA is "0". In Chen's study, the random walk algorithm can restart in each step when the current node is seed, while the random probabilities is set as r(0 < r < 1). p(t) is defined as a vector in which the i-th element holds the probability of finding the random walk at node i at step t[10]. Thus, the definition of the random walk algorithm is[10]:
| $ p\left( {t + 1} \right) = \left( {1-r} \right)Wp\left( t \right) + rp\left( 0 \right) $ | (1) |
where W is defined as miRNA-miRNA functional similarity matrix[10] and the value of r equals to 0.2. After some steps, the probability p is tending towards stability (the difference between p(t) and p(t+1) is less than 10-6), therefore, the candidate miRNAs are sorted according to the value of p. The high-scored miRNAs are chosen and believed to have a high feasibility to be associated with the current disease. The low-scored miRNAs are also reserved to be used later in this study.
2.2.2 Calculation of indirect miRNA-disease associationThe previous research has shown that the diseases are closely related to gene-gene and protein-protein interactions[25]. Furthermore, as is well known, miRNAs are associated with diseases via targeting to genes that are associated with various diseases. Thus, miRNA-disease associations could be inferred based on their targets gene indirectly. In this examination, we first download the relevant data according to Section 2.1 and construct a network which consists of three layers indicating miRNAs layer, genes layer and disease layer, respectively, shown as "Indirect computation" in Fig. 1. The association between each miRNA and disease is measured by the interactions between miRNA's target genes and disease-related genes. Based on the observations that genes causing the same or similar diseases often lie close to one another in a gene-gene interaction network[26-27]. Thus, the core process for computing indirect miRNA-disease association is the calculation of gene-gene similarity. So far, many approaches[28-30] for measuring gene functional similarity have been proposed based on Gene Ontology data. Teng[31] proposed the method called SORA which was used to measure gene functional similarity in GO context and their results showed that SORA was superior to the other five state-of-the-art methods. Thus, Teng's method is adopted to calculate gene-gene similarity. First, the information content (IC) of a term is computed making use of semantic specificity and coverage. The IC of the term is defined as:
| $ IC\left( {{t_i}} \right) = Specificity\left( {{t_i}} \right) \times \left( {1-\frac{{\log \left( {desc\left( {{t_i}} \right) + 1} \right)}}{{\log \left( {total\_terms} \right)}}} \right) $ | (2) |
where desc(ti) means the number of descendants of term ti, and total_terms is the number of terms in GO.Specificity(ti) is the semantic specificity of term ti, and is computed by its depth in the GO hierarchy. TA and TB are the collections of GO terms of gene GA and gene GB, respectively. That is, gene GA and GB are annotated with term sets TA={t1, t2, …, tm} and TB={t1, t2, …, tn}, respectively. The functional similarity of two genes GAand GB is defined as FS(GA, GB) and is estimated using the IC overlap ratio of term sets according to Eq.(2):
| $ FS\left( {{G_A}, {G_B}} \right) = \left( {\frac{{IC\left( {{T_A} \cap {T_B}} \right)}}{{IC\left( {{T_A}} \right)}} + \frac{{IC\left( {{T_A} \cap {T_B}} \right)}}{{IC\left( {{T_B}} \right)}}} \right)/2 $ | (3) |
In this examination, 17 011×7 709 gene pairs for human lung cancer, 1 658×7 709 gene pairs for human breast cancer, and 50×7 709 gene pairs for human colorectal cancer are computed.
Finally, for a given disease, a certain score is assigned to each candidate miRNA. The score is the sum of functional similarities which are computed between each of miRNA's target and each of disease-associated gene.
2.2.3 Decision fusion method for constructing reliable training datasetThe reliable training dataset is constructed by assigning high confidence class label to each miRNA in training dataset using decision fusion method. The advantages of both direct results and indirect results of miRNA-disease associations are combined to prioritize disease-associated and non-disease-associated miRNAs. According to the decision fusion method, the certain miRNA is assigned with the positive label unless it is prioritized as disease-associated one by both kinds of methods. The miRNA is assigned with the negative label unless it is prioritized as non-disease-associated one by both kinds of methods. The miRNA is assigned with the "doubtful" label if it is prioritized as disease-associated miRNA only in one kind of method. The process of decision fusion method is illustrated in Fig. 1. Finally, there are 136 positive miRNAs and 77 "doubtful" miRNAs in GSE68951, 235 positive miRNAs and 132 "doubtful" miRNAs in GSE58606, and 170 positive miRNAs and 67 "doubtful" miRNAs in GSE41655, respectively.
2.3 Prediction of Cancer-related MiRNAsMiRNA expression data are used in this study to discover the tissue and temporal specificity of miRNA-disease association. We want to capture the "state" and "transition" of consecutive expression states under a series of biological conditions. It is well known that models which include latent or hidden state structure may be more expressive than fully observable models, and can often find relevant substructure in a given domain. Thus, in this work, to predict disease-related miRNAs, we utilize HCRF[32] which use intermediate hidden variables to model the latent structure of the input miRNA expression profiling. HCRF defines a joint distribution over the class label and hidden state labels conditioned on the observations, with dependencies between the hidden variables expressed by an undirected graph. As is well known that the machine learning mo-dels can be more expressive when containing latent state structure. Furthermore, the relevant substructures in the domain can be found by these models. Thus, in this work, to predict disease-related miRNAs, we utilize HCRF[32] which use intermediate hidden variables to model the latent structure of the input miRNA expression profiling. HCRF defines a joint distribution over the class label (disease or non-disease associated) and hidden state labels conditioned on the observations (expression values). The graphical model representation of HCRF is shown in Fig. 2.The hollow circles are hidden variables and the gray circles are observed variables. The dotted line between h and x denotes the dependence of h on the observation x.

|
Figure 2 The graphical model representation of HCRF |
In this study, the mapping of observations x (miRNAs) to class labels y∈Y (diseases) is investigated, where x={x1, x2, …, xm}. Each xi is represented by a feature vector xi={xi, 1, xi, 2, …, xi, m} for i=1, 2, …, n, and xi, j corresponds to the jth feature of the ith miRNA. The training set consists of labeled examples (xi, yi).For any xi, given a latent variables h={h1, h2, …, hm}, hj is a member of a finite set H of possible hidden labels in the model, and each hj corresponds to a labeling of xi with some member of H, which may correspond to "part" structure of observation x and capture more context of the entire sequence.To predict the corresponding label y according to the input x, the HCRF models the conditional probability of a class label given a set of observations by:
| $ \begin{array}{l} P\left( {y, h\left| {x, \theta } \right.} \right) = \sum\limits_h {P\left( {y, h\left| {x, \theta } \right.} \right)} = \\ \;\;\;\;\frac{1}{{{Z_X}\left( \theta \right)}}\exp \left( {\psi \left( {y, h, x;\theta } \right)} \right) \end{array} $ | (4) |
where θ is the parameter of model, and ψ(y, h, x; θ)∈R is a potential function parameterized by θ. Marginalizing over h yields following form:
| $ \begin{array}{l} P\left( {y\left| {x;\theta } \right.} \right) = \sum\limits_h {P\left( {y, h\left| {x;\theta } \right.} \right)} = \\ \;\;\;\;\frac{1}{{{Z_x}\left( \theta \right)}}\sum\limits_h {e\left( {\psi \left( {y, h, x;\theta } \right)} \right)} \end{array} $ | (5) |
where
| $ \begin{array}{l} \psi \left( {y, h, x, \theta } \right) = \sum\limits_{j = 1}^m {\sum\limits_l {f_l^1\left( {j, y, {h_j}, x} \right)\theta _l^1 + } } \\ \;\;\;\;\;\sum\limits_{\left( {j.k} \right) \in E} {\sum\limits_l {f_l^2\left( {j, k, y, {h_j}, {h_k}, x} \right)\theta _l^2} } \end{array} $ | (6) |
where l is the serial number of feature function, fl1 and fl2 are functions defining the features in the model, and θ={θl1, θl2} are parameters that can be learnt from training data.fl1 is associated with a single hidden state variable, while fl2 relies on two connected hidden state variables in the model. Given the test sample x and the parameter θ*, the label is defined as arg maxy∈YP(y|x, θ*), where θ* can be induced from a training set. Following previous studies on Conditional Random Field (CRF)[33], the following objective function is used to estimate the parameters:
| $ L\left( \theta \right) = \sum\limits_i {\log P\left( {{y_i}\left| {{x_i}, \theta } \right.} \right)-} \frac{1}{{2{\sigma ^2}}}{\left\| \theta \right\|^2} $ | (7) |
The first term in Eq.(7) is the log-likelihood of the data. The second term is the log of a Gaussian prior with variance σ2, for example,
| $ P\left( \theta \right) \sim \exp \left( {-\frac{1}{{2{\sigma ^2}}}{{\left\| \theta \right\|}^2}} \right) $ |
Gradient ascent method is used to search for the optimal parameter values, θ*=arg maxθL(θ), under this criterion.
3 Results and Discussions 3.1 Performance EvaluationTo evaluate the ability of the method proposed in this study in predicting disease-associated miRNAs, 5-fold cross validation was performed. For a specific miRNA expression profiling, the experimentally validated disease-associated miRNAs are divided into five subsets, four of which are used as known information for predicting candidates, while the others are used as test samples.
Because miRNA functions are spatial and temporal-specific, a certain disease-associated miRNA does not have to express at every development stage of disease. Thus, there are 3 labels in our training data, (1) positive label: the miRNAs with this label are inferred as disease-associated miRNAs from the current training data, (2) doubtful label: the miRNAs with this label is believed to be associated with the disease but could not be inferred from the current training data, and (3) negative label: the miRNAs with this label are inferred as non-disease-associated miRNAs from the current training data. Here, in the step of performance evaluation, the candidate miRNA is regarded as the positive one as long as it is not predicted as a negative class, regardless of whether it belongs to a positive class or a doubtful class.
Finally, the receiver operating characteristics (ROC) curve is plotted according to true positive rate (TPR) versus false positive rate (FPR) at different thresholds and the results are shown in Fig. 3 and Table 1. Sensitivity refers to the percentage of the test miRNAs which are predicted as positive ones and specificity stands for the percentage of miRNAs which are predicted as negative ones. In Fig. 3, the curve with arrow denotes the ROC of GSE68951, the curve with rhombus stands for the ROC of GSE41655, and the last curve denotes the ROC of GSE58606. The area under ROC curve (AUC) is calculated, and the values of AUC are 0.656 8, 0.727 2, and 0.699 3 corresponding to GSE68951, GSE58606 and GSE41655, respectively.
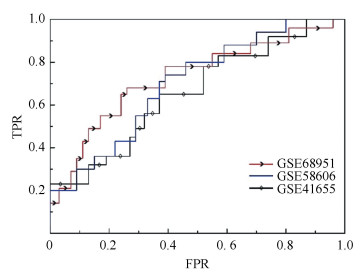
|
Figure 3 The ROC of HCRF performance on three miRNA expression data |
| Table 1 Prediction methods of decision fusion method and direct and indirect computation methods |
3.2 Reliability of Decision Fusion Method
To make sure that the step of decision fusion contributes to the final predictions, the reliability of newly constructed training data described in Section 2.2.3 is examined. The direct and indirect computational methods described in Section 2.2.1 and Section 2.2.2 are two kinds of classic algorithms for miRNA-disease association prediction. Here, the performances of decision fusion method and these two kinds of methods are compared. The ROC curves are used to evaluate the predictive performance, which plots true-positive rate (TPR) versus false-positive rate (FPR) at different rank cutoffs. It can be seen from Fig. 4 that the results of the decision fusion method (curve with arrow) are superior to those of both the direct computational method (normal curve) and the indirect computational method (curve with rhombus) under the condition of three cancers. The areas under the curve with arrow are 0.804, 0.882 and 0.847 for human lung cancer, human breast cancer and human colorectal cancer, respectively. All above results demonstrate that decision fusion method can combine the advantage of previous methods and contributes to the superior performance of HCRF.

|
Figure 4 The ROC representation of comparison between decision fusion method and direct and indirect computation method |
3.3 Accuracy Compared with Other Tools
As far as we know, there is no study making use of miRNA expression profiling to predict potential disease-associated miRNAs prior to this. Because HCRF is inspired by Hidden Markov Model (HMM)[34] and CRF, the superiorities of HCRF model comparing with HMM and CRF are investigated. The AUC results on GSE68951, GSE58606 and GSE41655 are shown in Table 2. As can be seen, HCRF outperforms other models significantly, which demonstrate the ability of HCRF in detecting the variation trend among a series of miRNA expression values.
| Table 2 Prediction results of HCRF, HMM and CRF model |
Furthermore, the comparison between HCRF and existing classic methods are also performed. For example, RWRMDA adopts global network similarity measure and implements random walk method on the network to infer potential miRNA-disease interactions. MiRPD is a model in which miRNA-disease associationsare inferred indirectly by coupling miRNA-protein associations with protein-disease associations. Jiang's method[9] made use of network similarity measure and applied hypergeometric distribution to the network integrated with the neighbor information. The ROC of above four methods is shown in Fig. 5 and the corresponding AUC is shown in Table 3. In Fig. 5, the curve with arrow denotes the results of HCRF and the AUC is 0.656 8, 0.727 2 and 0.699 3 on three miRNA expression profiling, respectively. The normal curve stands for the results of RWRMDA method, the curve with "+" presented the results of miRPD method and the dotted curve denotes the results of Jiang's methods. It can be seen that the proposed method in this study outperforms other methods obviously.

|
Figure 5 The ROC representation of comparison between HCRF and RWRMDA, miRPD and Jiang's method |
| Table 3 Comparison between HCRF and previous methods |
3.4 Functional Enrichment Analysis
For each kind of disease investigated in this study, the proposed method identifies a certain number of miRNAs and deduces that these miRNAs are associated with the disease. To investigate the reasonability of the proposed method, the functional enrichment analysis is performed based on TAM[35]on 136 known and top 50 predicted lung cancer-associated miRNAs, 25 known and top 63 predicted breast cancer-related miRNAs and 170 known miRNAs and top 50 predicted colorectal cancer-related miRNAs. TAM is a web accessible tool developed by Lu et al.[35] for identifying overrepresented or underrepresented miRNA categories for a given list of miRNAs. Finally, the results of TAM on GSE68951 are shown as Fig. 6 (the results of GSE58606 and GSE41655 are shown in supplementary materials). The horizontal ordinate denotes the number of miRNAs that significant enriched in each function. The vertical coordinate stands for the 38 significant enriched functions. For human lung cancer, the results show 32 miRNAs have a function called tumor suppressors, 35 miRNAs are considered to be associated with cell death, 31 miRNAs are considered to be associated with apoptosis, and 42, 34, 20, 21 miRNAs are concerned with human embryonic stem cell regulation, hormones regulation, adipocyte differentiation, inflammation, respectively. The false discovery rate of these miRNAs is given by TAM ranges from 9.41E-18 to 2.94E-05. In the last few years, with the development of biological experimental technology, most of the predictions have been validated, which play an critical role in the process of disease development[10].
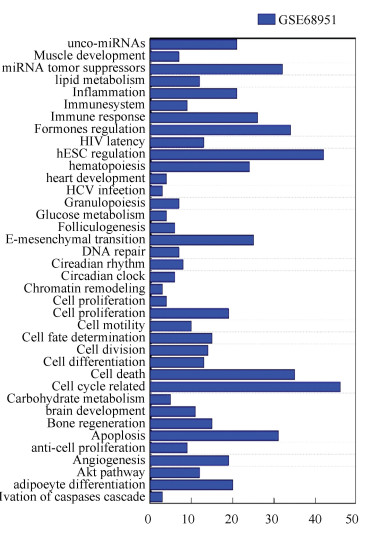
|
Figure 6 Functional enrichment analysis of lung cancer-related miRNAs |
4 Conclusions
The identification of disease-associated miRNAs is beneficial to the disease diagnosis and prognosis. In this study, HCRF model is applied to miRNA expression profiling to infer potential miRNA-disease associations. There are two advantages of proposed method in this work comparing with previous methods: (1) the limited information of miRNA function and target mechanism restricts the development of network similarity measure method. However, more and more expression profiling data are available which show the broad prospects and necessity for investigating miRNA-disease association using expression data, (2) the network similarity measure method could not reflect the tissue and temporal specificity of miRNA function, while miRNA expression profiling could.
Finally, the proposed method in this examination is compared with other prediction methods and achieves superior performance. Because decision fusion method is used in this study to construct reliable training data, the performance of decision fusion method is checked. Furthermore, the comparison between HCRF and classic methods such as RWRMDA, miRPD and Jiang's method are performed. The results demonstrate HCRF has obviously high accuracy in inferring potential miRNA-disease associations, which implies the great potential of HCRF model and expression profiling for the discovery of potential miRNA-disease association.
| [1] |
Bartel D P. Micrornas: Genomics, biogenesis, mechanism, and function. Cell, 2004, 116(2): 281-297. DOI:10.1016/S0092-8674(04)00045-5 ( 0) 0)
|
| [2] |
Lu M, Zhang Q, Deng M, et al. An analysis of human microrna and disease associations. PLoS One, 2008, 3(10): e3420. DOI:10.1371/journal.pone.0003420 ( 0) 0)
|
| [3] |
Cheng A M, Byrom M W, Shelton J, et al. Antisense inhibition of human mirnas and indications for an involvement of mirna in cell growth and apoptosis. Nucleic Acids Res, 2005, 33(4): 1290-1297. DOI:10.1093/nar/gki200 ( 0) 0)
|
| [4] |
Bandyopadhyay S, Mitra R, Maulik U, et al. Development of the human cancer microrna network. Silence, 2010, 1(1): 6. DOI:10.1186/1758-907X-1-6 ( 0) 0)
|
| [5] |
Yang H, Dinney C P, Ye Y, et al. Evaluation of genetic variants in microrna-relate genes and risk of bladder cancer. Cancer Res, 2008, 68(7): 2530-2537. DOI:10.1158/0008-5472.CAN-07-5991 ( 0) 0)
|
| [6] |
Kantharidis P, Wang B, Carew R M, et al. Diabetes complications: The microrna perspective. Diabetes, 2011, 60(7): 1832-1837. DOI:10.2337/db11-0082 ( 0) 0)
|
| [7] |
Junn E, Mouradian M M. Micrornas in neurodegenerative diseases and their therapeutic potential. Pharmacol Ther, 2012, 133(2): 142-150. DOI:10.1016/j.pharmthera.2011.10.002 ( 0) 0)
|
| [8] |
Kozomara A, Griffiths-Jones S. Mirbase: Annotating high confidence micrornas using deep sequencing data. Nucleic Acids Res, 2014, 42: D68-D73. DOI:10.1093/nar/gkt1181 ( 0) 0)
|
| [9] |
Jiang Q, Hao Y, Wang G, et al. Prioritization of disease microRNAs through a human phenome-micrornaome network. BMC Syst Biol, 2010, 4(Suppl 1): S2. DOI:10.1186/1752-0509-4-S1-S2 ( 0) 0)
|
| [10] |
Chen X, Liu M X, Yan G Y. RWRMDA: Predicting novel human microrna-disease associations. Mol Biosyst, 2012, 8(10): 2792-2798. DOI:10.1039/c2mb25180a ( 0) 0)
|
| [11] |
Chen H, Zhang Z. Similarity-based methods for potential human microrna-disease association prediction. BMC Med Genomics, 2013, 6: 12. DOI:10.1186/1755-8794-6-12 ( 0) 0)
|
| [12] |
Mork S, Pletscher-Frankild S, Palleja Caro A, et al. Protein-driven inference of mirna-disease associations. Bioinformatics, 2014, 30(3): 392-397. DOI:10.1093/bioinformatics/btt677 ( 0) 0)
|
| [13] |
Zhang F, Lu M, Zhang Q P, et al. Prediction of the micrornas related to cardiovascular diseases by bioinformatics. Beijing Da Xue Xue Bao, 2009, 41(1): 112-116. ( 0) 0)
|
| [14] |
Takamizawa J, Konishi H, Yanagisawa K, et al. Reduced expression of the let-7 micrornas in human lung cancers in association with shortened postoperative survival. Cancer Res, 2004, 64(11): 3753-3756. DOI:10.1158/0008-5472.CAN-04-0637 ( 0) 0)
|
| [15] |
Rosenfeld N, Aharonov R, Meiri E, et al. Micrornas accurately identify cancer tissue origin. Nat Biotechnol, 2008, 26(4): 462-469. DOI:10.1038/nbt1392 ( 0) 0)
|
| [16] |
Volinia S, Calin G A, Liu C G, et al. A microrna expression signature of human solid tumors defines cancer gene targets. Proc Natl Acad Sci U S A, 2006, 103(7): 2257-2261. DOI:10.1073/pnas.0510565103 ( 0) 0)
|
| [17] |
Zang W, Wang Y, Du Y, et al. Differential expression profiling of micrornas and their potential involvement in esophageal squamous cell carcinoma. Tumour Biol, 2014, 35(4): 3295-3304. DOI:10.1007/s13277-013-1432-5 ( 0) 0)
|
| [18] |
Lu J, Getz G, Miska E A, et al. MicroRNA expression profiles classify human cancers. Nature, 2005, 435(7043): 834-838. DOI:10.1038/nature03702 ( 0) 0)
|
| [19] |
Xiao F, Zuo Z, Cai G, et al. miRecords: an integrated resource for microRNA-target interactions. Nucleic Acids Res, 2009, 37(Database issue): D105-D110. DOI:10.1093/nar/gkn851 ( 0) 0)
|
| [20] |
Pletscher-Frankild S, Palleja A, Tsafou K, et al. DISEASES: text mining and data integration of disease-gene associations. Methods, 2015, 74: 83-89. DOI:10.1016/j.ymeth.2014.11.020 ( 0) 0)
|
| [21] |
Li Y, Qiu C, Tu J, et al. HMDD v2.0: a database for experimentally supported human microRNA and disease associations. Nucleic Acids Res, 2014, 42(Database issue): D1070-D1074. DOI:10.1093/nar/gkt1023 ( 0) 0)
|
| [22] |
Gene Ontology C. Gene ontology consortium: Going forward. Nucleic Acids Res, 2015, 43(Database issue): D1049-D1056. DOI:10.1093/nar/gku1179 ( 0) 0)
|
| [23] |
Xuan P, Han K, Guo M, et al. Prediction of microRNAs associated with human diseases based on weighted k most similar neighbors. PLoS One, 2013, 8(8): e70204. DOI:10.1371/journal.pone.0070204 ( 0) 0)
|
| [24] |
Wang D, Wang J, Lu M, et al. Inferring the human microrna functional similarity and functional network based on microRNA-associated diseases. Bioinformatics, 2010, 26(13): 1644-1650. DOI:10.1093/bioinformatics/btq241 ( 0) 0)
|
| [25] |
Vanunu O, Magger O, Ruppin E, et al. Associating genes and protein complexes with disease via network propagation. PLoS Comput Biol, 2010, 6(1): e1000641. DOI:10.1371/journal.pcbi.1000641 ( 0) 0)
|
| [26] |
Oti M, Snel B, Huynen M A, et al. Predicting disease genes using protein-protein interactions. J Med Genet, 2006, 43(8): 691-698. DOI:10.1136/jmg.2006.041376 ( 0) 0)
|
| [27] |
Oti M, Brunner H G. The modular nature of genetic diseases. Clin Genet, 2007, 71(1): 1-11. DOI:10.1111/j.1399-0004.2006.00708.x ( 0) 0)
|
| [28] |
Pesquita C, Faria D, Bastos H, et al. Metrics for GO based protein semantic similarity: a systematic evaluation. BMC Bioinformatics, 2008, 9(Suppl 5): S4. DOI:10.1186/1471-2105-9-S5-S4 ( 0) 0)
|
| [29] |
Valentini G. True path rule hierarchical ensembles for genome-wide gene function prediction. IEEE/ACM Trans Comput Biol Bioinform, 2011, 8(3): 832-847. DOI:10.1109/TCBB.2010.38 ( 0) 0)
|
| [30] |
Yang H, Nepusz T, Paccanaro A. Improving GO semantic similarity measures by exploring the ontology beneath the terms and modelling uncertainty. Bioinformatics, 2012, 28(10): 1383-1389. DOI:10.1093/bioinformatics/bts129 ( 0) 0)
|
| [31] |
Teng Z, Guo M, Liu X, et al. Measuring gene functional similarity based on group-wise comparison of GO terms. Bioinformatics, 2013, 29(11): 1424-1432. DOI:10.1093/bioinformatics/btt160 ( 0) 0)
|
| [32] |
Quattoni A, Wang S, Morency L-P, et al. Hidden conditional random fields. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2007, 10: 1848-1852. ( 0) 0)
|
| [33] |
Lafferty J D, McCallum A, Pereira F C N. Conditional random fields: Probabilistic models for segmenting and labeling sequence data. Proceedings of the Eighteenth International Conference on Machine Learning. San Francisco, CA: Morgan Kaufmann Publishers Inc., 20014, 282-289.
( 0) 0)
|
| [34] |
Baum L E, Petrie T, Soules G, et al. A maximization technique occurring in the statistical analysis of probabilistic functions of markov chains. The Annals of Mathematical Statistics, 1970, 41(1): 164-171. DOI:10.1214/aoms/1177697196 ( 0) 0)
|
| [35] |
Lu M, Shi B, Wang J, et al. Tam: A method for enrichment and depletion analysis of a microrna category in a list of micrornas. BMC Bioinformatics, 2010, 11: 419. DOI:10.1186/1471-2105-11-419 ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


