2. School of Municipal and Environmental Engineering, Harbin Institute of Technology, Harbin 150001, China;
3. Université de Lyon, CNRS, INSA-Lyon, Université Claude Bernard Lyon 1, CETHIL UMR5008, F-69621, Villeurbanne, France
Proper orthogonal decomposition (POD), which also be called as Karhunen-Loève (K-L) decomposition, is an unbiased method to capture the most 'energetic' spatial structures and provide a means of constructing low-dimensional model (LDM) for complex dynamic system. POD was firstly introduced into turbulent field by Lumley[1] for studying coherent structures. Sirovich[2] proposed an effective approach, the method of snapshots, which remarkably reduced the computational time and cost. Since then, POD has been used extensively for recognizing turbulent coherent structures in many fluid flows on the basis of experimental data and numerical calculation data[3-6], such as boundary layer flow, cavity flow, jet flow, turbulent convective flow, polymer drag-reducing flows[7-9], etc.
The most attractive advantage of POD is to build LDM using Galerkin projection onto the empirical basis functions (also called as eigenfunctions or eigenmodes or modes) obtained from POD. LDM can descript the dynamic characteristics of difficult issues with a small degree of freedom. On account of the above characteristic, POD-LDM has been widely used in both science and engineering. For example, POD-LDM can be used for the stability analysis[10] and chaotic analysis[11-14] of turbulent flow system. Also, POD-LDM has been used for flow control in engineering application[15-18], such as, to decrease flow drag based on the control scheme coupling with POD-LDM, etc. But, it is very difficult to realize the flow control based on the traditional method due to the disadvantage of long-time calculated feedback. Therefore, the study on POD-LDM is extremely meaningful.
Researchers have made many efforts to establish reliable LDMs in fluid flow and heat transfer fields. In fluid flow aspects, Aubry et al.[19] established the model of the wall region boundary layer of turbulent flow using the linear combination of POD eigenfunction. Then, Berkooz et al.[20] found some obvious relationship between the dynamics characteristics of coherent structures in the turbulent boundary layer and LDM developed by Aubry[19]. Cazemier et al.[10] established a LDM based on POD-Galerkin for a square lid-driven cavity. It was found that a closure scheme is demanded to correct the 80-dimensional dynamic system (based on 80 POD eigenmodes) over time, that is to say, it is difficult to predict the dynamical characteristics of flow for long time based on 80-dimensional LDM. Noack et al.[21] proposed a low-dimensional by Galerkin projection for the incompressible, viscous flow around a cylinder. The model can descript the flow of different Reynolds number in a high accuracy. Now, LDMs have been built in many fluid flows[22-24], such as, channel flow, cylinder flow, plane Couette flow, etc. In heat transfer aspects, Banerjee et al.[25] established a LDM based on POD-Galerkin for thermal processing system, and the simulation results with LDM are well agreement with steady state and transient data calculation by the Finite Element Method. Białecki et al[26] studied the processing of time-dependent boundary conditions, non-homogeneous initial condition ensure the error in a LDM based on POD-Galerkin for 3D problem of a radiator and 2D gas cooled turbine blade. Wang et al.[27] compared POD projection methods and POD interpolation for quick and accurate prediction of heat transfer questions; the results show that the method of POD projection is more quick and accurate than POD interpolation method. Recently, Han et al.[28-29] proposed a low dimension model by the POD-Galerkin projection method rely on a body-fitted coordinate system. This method has been successfully used in steady heat transfer problem and unsteady-state variable-property heat transfer problem.
Although LDMs based on POD-Galerkin have been derived by thinking about the flow without heat transfer characteristics and heat transfer without flow characteristics, they have also been applied to some of thermal fluid problems described by the incompressible Boussinesq equations, such as natural convection in air-cooling system[30], turbulent mixed convection[31-32], and Rayleigh-Bénard (RB) convection[33], etc. RB convection is one of the most classical thermal convection, which widely appears in many practical engineering and has attracted much attention. Sirovich and co-workers[34-37] firstly studied the RB convection based on POD procedure. Dean and Sirovich[36] made a parametric study of the POD energy spectrum for small Rayleigh number Ra≤4.6×104. Tarman[38] proposed an improved dynamical approximation to Boussinesq equation at Prandtl number Pr=0.72 and Ra=104. San and Borggaard[39] researched the closure scheme for POD models in a RB convection at Pr=0.71 and Ra=3.4×105. Recently, Bailon-Cuba and Schumacher studied the RB convection in a three-dimensional square domain at Pr=0.7 and Ra=1.03×105.
Through lots of studies on RB convection based on POD, we can deeply understand this complex thermal convection system from POD spectrum, modes and dynamical characteristics. However, most studies focus on the RB convection at low Ra. How about the dynamical characteristics for the RB convection at high Ra? This is our purpose to investigate this important problem in this paper. Firstly, we used direct numerical simulations (DNS) to obtain the data for POD procedures in Section 2. Then we analyze the POD energy spectrum and eigenmodes in Section 3. The LDM based on POD-Galerkin is built and short-time dynamical characteristics are analyzed in Section 4. Finally, the summary and outlook are drawn in Section 5.
2 Rayleigh-Bénard Convection Model and Numerical SchemeRayleigh-Bénard convection, i.e., the buoyancy driven flow of a fluid heated from below and cooled from above in a cavity, is an important problem in fluid flow aspect[40]. In this paper, two-dimensional RB convection is simulated in a Cartesian domain defined by the orthonormal vector base (ex, ey) where x and y are horizontal direction and vertical direction, respectively, as shown in Fig. 1.
|
Figure 1 Schematic diagram of the simulation domain |
In this paper, Rayleigh-Bénard convection is incompressible flow, and the buoyancy effect is simulated using the Boussinesq approximation. The dimensionless equations are shown as follows:
| $ \left\{ \begin{array}{l} \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0\\ \frac{{\partial {u_i}}}{{\partial t}} + {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + {\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\frac{{{\partial ^2}{u_i}}}{{\partial {x_j}\partial {x_j}}} + \mathit{\Theta }{{\mathit{ δ} }_{i2}}\\ \frac{{\partial \mathit{\Theta }}}{{\partial t}} + {u_j}\frac{{\partial \mathit{\Theta }}}{{\partial {x_j}}} = \frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\frac{{{\partial ^2}\mathit{\Theta }}}{{\partial {x_j}\partial {x_j}}} \end{array} \right. $ | (1) |
where ui(i=1, 2) is dimensionless velocity by rescaling with uc(
Eq.(1) is solved based on the software OpenFOAM. Euler method was used for time derivatives (time step Δt=10-3) and Gauss linear method was used for spatial derivatives. The boundary conditions: for velocity, no-slip at the walls; for temperature, the temperature for the top wall was TC=0 and those for the bottom wall was TH=1; the left and right walls were kept insulated, i.e., əT/əx=0. The initial conditions: for velocity, ui=0; and for temperature, Θ=0.5. All simulations are performed with the resolution 256×256. At each instant, the heat flux averaged over the hot wall can be represented by Nusselt number, Nu, defined as:
| $ N{u_H} = - \int_0^1 {\frac{{\partial \mathit{\Theta }}}{{\partial x}}} \left| {_{y = 0}} \right.{\rm{d}}x $ |
Firstly, we need to check our code. For a comparison, we calculated RB convection at four different Ra number. The results are compared with the outcome in Quertatani et al.[41] and Turan et al.[42], as shown in Table 1. It can be found clearly from Table 1 that the present results agree extremely well with the corresponding studies in Refs. [41] and [42]. It suggests that the DNS code in OpenFOAM is correct.
| Table 1 Comparison of present simulations with theresults by Quertatani et al. and Turan et al. based on NuH |
Fig. 2 displays the classical velocity vector and isothermal contours for RB convection at Ra=107. It is obviously that the flow is fully turbulence and there exists a large-scale circulation structure (LSC) in the cavity. LSC carries the heat from the hot wall to the cold wall. Two secondary eddies are observed at the top right and bottom left corners. But to point out, the rotation direction of LSC and the location of two secondary eddies are random.
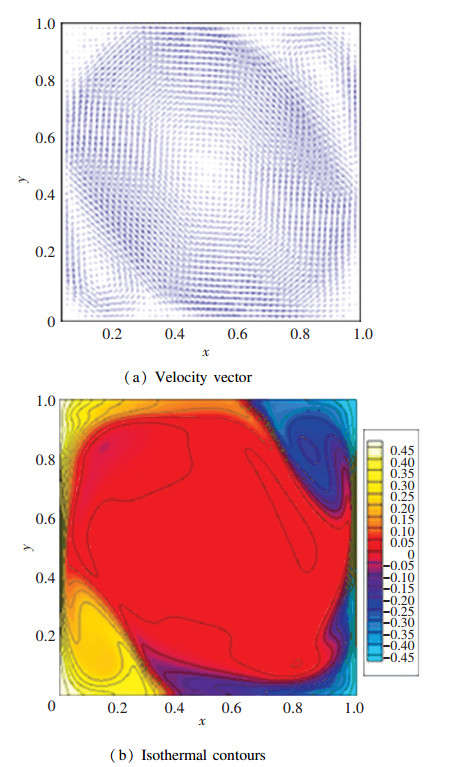
|
Figure 2 The velocity vector and isothermal contours for Ra=106 from DNS data |
3 POD Analysis for Rayleigh-Bénard Convection 3.1 POD Procedure
Proper orthogonal decomposition is a model reduction technique that extracts the most energetic modes from a set of realizations or snapshots of the flow. Here, the basics of POD procedure is introduced in brief. Lumley[1] firstly proposed the POD method, which is used as an objective method to diagnosis the deterministic characteristics in turbulent flows. A coherent structure is defined as a function of the spatial variables that have maximum energy content in Lumley's theory. In other words, coherent structures are linear combinations of σ(x)'s which maximize the following expresion[43]:
| $ \frac{{\left\langle {{{\left( {\mathit{\boldsymbol{\sigma }}\left( \mathit{\boldsymbol{x}} \right),\mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right)}^2}} \right\rangle }}{{\left( {\mathit{\boldsymbol{\sigma }}\left( \mathit{\boldsymbol{x}} \right),\mathit{\boldsymbol{\sigma }}\left( \mathit{\boldsymbol{x}} \right)} \right)}} $ | (2) |
In Eq.(2),
| $ \int\limits_\mathit{\Omega } {\mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x'}}} \right)\mathit{\boldsymbol{\sigma }}\left( {\mathit{\boldsymbol{x'}}} \right){\rm{d}}\mathit{\boldsymbol{x'}}} = \lambda \mathit{\boldsymbol{\sigma }}\left( \mathit{\boldsymbol{x}} \right) $ | (3) |
where R(x, x′) is the space-correlation tensor:
| $ \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x'}}} \right) = \left\langle {\mathit{\boldsymbol{u}}\left( \mathit{\boldsymbol{x}} \right),{\mathit{\boldsymbol{u}}^{\rm{T}}}\left( {\mathit{\boldsymbol{x'}}} \right)} \right\rangle $ | (4) |
By solving expression (3), the first POD eigenfunction can be obtained; in the same way, the second largest eigenfunction can also be calculated by the similar procedure of those for the first eigenfunction:
| $ \mathop {\max }\limits_{\sigma \in {L^2}} \frac{{\left\langle {{{\left( {\mathit{\boldsymbol{\sigma }},\mathit{\boldsymbol{u}} - \left( {\mathit{\boldsymbol{u}},\mathit{\boldsymbol{\sigma }}} \right)\mathit{\boldsymbol{\sigma }}} \right)}^2}} \right\rangle }}{{\left( {\mathit{\boldsymbol{\sigma }},\mathit{\boldsymbol{\sigma }}} \right)}} $ | (5) |
It can be easily proved that the nth POD basic function should make the maximum of expression (6):
| $ \mathop {\max }\limits_{\sigma \in {L^2}} \frac{{\left\langle {{{\left( {{\mathit{\boldsymbol{\sigma }}_n},\mathit{\boldsymbol{u}} - \sum\limits_{i = 1}^{n - 1} {\left( {\mathit{\boldsymbol{u}},{\mathit{\boldsymbol{\sigma }}_i}} \right){\mathit{\boldsymbol{\sigma }}_i}} } \right)}^2}} \right\rangle }}{{\left( {{\mathit{\boldsymbol{\sigma }}_n},{\mathit{\boldsymbol{\sigma }}_n}} \right)}} $ | (6) |
The eigenfunctions gotten by this way are orthogonal to each other, that is:
| $ \left( {{\mathit{\boldsymbol{\sigma }}_i},{\mathit{\boldsymbol{\sigma }}_j}} \right) = {\delta _{ij}} $ | (7) |
The closure of the span of the POD eigenfunctions is equal to the set of all realizable flow fields. Therefor it can be used as a basis for flow field.
| $ \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{i = 1}^\infty {{a_i}\left( t \right){\mathit{\boldsymbol{\sigma }}_i}\left( \mathit{\boldsymbol{x}} \right)} $ | (8) |
The coefficients ai(t) in Eq.(8) can be gotten by:
| $ {a_i}\left( t \right) = \left( {\mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right),{\mathit{\boldsymbol{\sigma }}_i}\left( \mathit{\boldsymbol{x}} \right)} \right) $ | (9) |
The coefficients an(t) are independent and the mean values of them are the eigenvalues λn:
| $ < {a_n}\left( t \right){a_m}\left( t \right) > = {\delta _{nm}}{\lambda _n} $ | (10) |
In other words, an(t)2 is the energy content of u(x, t) of σn(x). The total energy is the sum of an(t)2:
| $ E = \left( {\mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right),\mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right)} \right) = \sum\limits_{n = 1}^N {{a_n}{{\left( t \right)}^2}} = \sum\limits_{n = 1}^N {{\lambda _n}} $ | (11) |
E is twice the average turbulent kinetic energy. The magnitude of the nth eigenvalue λn represents the average kinetic energy in the nth mode σn(x)
| $ {E_n} = \frac{{{\lambda _n}}}{E} $ | (12) |
In the above POD procedure, it is found that to determine the POD eigenfunctions, it takes much time to solve the Fredholm integral equation (3), that is to say, calculation the equation (3) directly would exceed today's computer ability. In 1987, Sirovich[2] proposed the 'snapshot POD' method to solve this problem. Here, each instantaneous DNS data or PIV measurement from experiments (PIV: particle image velocimetry) is considered as a snapshot of the original flow. In the following, the snapshot POD is introduced in brief.
Firstly, the N snapshots are chosen. then it needs to calculate the mean field, which can be considered as the zeroth POD eigenfunction. The rest of the analysis concerns the fluctuating velocity, whose component can be denoted by (unj, vnj, wnj), here index n runs through the N snapshots and j runs M positions of velocity vectors in a given snapshot. All fluctuating velocity components from the N snapshots are arranged in a matrix U as[44]:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}} = \left[ {{\mathit{\boldsymbol{u}}_1},{\mathit{\boldsymbol{u}}_2},{\mathit{\boldsymbol{u}}_3}, \cdots ,{\mathit{\boldsymbol{u}}_{N - 1}},{\mathit{\boldsymbol{u}}_N}} \right] = }\\ {\left( {\begin{array}{*{20}{c}} {u_1^1}&{u_2^1}& \cdots &{u_N^1}\\ \vdots&\vdots&\vdots&\vdots \\ {u_1^M}&{u_2^M}& \cdots &{u_N^M}\\ {v_1^1}&{v_2^1}& \cdots &{v_N^1}\\ \vdots&\vdots&\vdots&\vdots \\ {v_1^M}&{v_2^M}& \cdots &{v_N^M}\\ {w_1^1}&{w_2^1}& \cdots &{w_N^1}\\ \vdots&\vdots&\vdots&\vdots \\ {w_1^M}&{w_2^M}& \cdots &{w_N^M} \end{array}} \right)} \end{array} $ | (13) |
The autocovariance matrix is constructed as[33]:
| $ \mathit{\boldsymbol{\tilde C}} = {\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}} $ | (14) |
and the corresponding eigenvalue problem should be solved:
| $ \mathit{\boldsymbol{\tilde C}}{\mathit{\boldsymbol{A}}_i} = {\lambda _i}{\mathit{\boldsymbol{A}}_i} $ | (15) |
The results are arranged based on the size of eigenvalues, thus
| $ {\lambda _1} > {\lambda _2} > \cdots > {\lambda _N} = 0 $ | (16) |
The eigenvectors of Eq.(15) make up a basis for expressing the POD eigenfunction σi(x),
| $ {\mathit{\boldsymbol{\sigma }}_i}\left( \mathit{\boldsymbol{x}} \right) = \frac{{\sum\limits_{n = 1}^N {\mathit{\boldsymbol{A}}_n^i{\mathit{\boldsymbol{u}}_n}} }}{{\left\| {\sum\limits_{n = 1}^N {\mathit{\boldsymbol{A}}_n^i{\mathit{\boldsymbol{u}}_n}} } \right\|}},i = 1,2 \cdots ,N $ | (17) |
where Ani is the nth component of the eigenvector corresponding to λi from Eq.(15) and the discrete 2-norm is defined as[33]:
| $ \left\| \mathit{\boldsymbol{y}} \right\| = \sqrt {y_1^2 + y_2^2 + \cdots + y_M^2} $ | (18) |
The POD eigenfunction σi(x) make up a set of orthogonality basic functions, and each snapshot can be reconstructed as[44]:
| $ {\mathit{\boldsymbol{u}}_n}\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{i = 1}^N {a_n^i\left( t \right){\mathit{\boldsymbol{\sigma }}_i}\left( \mathit{\boldsymbol{x}} \right)} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{a}}_n} $ | (19) |
where an=ΦTun and Φ=[σ1, σ2…σN-1].
3.3 POD Analysis ResultsWe approximated the POD eigenfunctions (or eigenmodes) using 200 snapshots. The relative contribution of each POD eigenmode is displayed in Fig. 3. From Fig. 3, it clearly shows that the fluctuating energy in the first eigenmodes is larger, however, high-order eigenmodes contains small fluctuating energy and the distribution is uniform. Table 2 lists the accumulative energy of the fluctuating velocity for first several eigenmodes. It is can be found that the first eigenmode contains (on average) 23.94% of the fluctuating energy. Coherent structures are seen as the sum of several eigenmodes that possess a dominant energy of the flow over 90%. From Table 2, we can find that the demanded numbers of eigenmodes is 10. So from the theory, it is sufficient to construct the LDM for RB convection using only 10 eigenmodes, which can reflect the original flow system. For a comparison, we also choose 30 and 50 eigenmodes to build LDM. The results will be discussed in Sections 4.2.
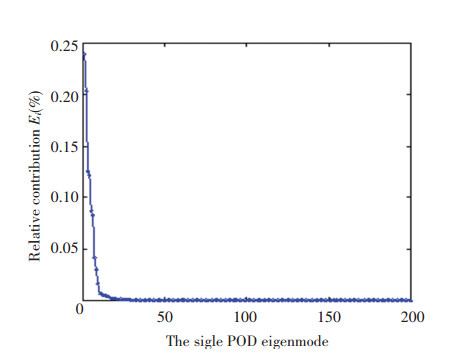
|
Figure 3 The relative energy for each POD eigenmode |
| Table 2 The accumulative energy of the projection of fluctuating velocity field on the first N-th POD eigenmodes |
The fluctuating velocity or fluctuating temperature fields can be reconstructed by these POD eigenmodes. It is important to study these POD eigenmodes. Fig. 4 shows vector plots of the averaged velocity field and 1st, 2nd, 3rd, 4th and 50th POD eigenmodes of fluctuating velocity field. It can be clearly seen that the averaged velocity field depicts the main characteristics of RB convection, i.e., there exists a LSC structure and two secondary eddies. The dominant flow structures are represented by the first leading eigenmodes. Also, it is important that the flow structures behave in an increasingly complex way and their spatial scale decreases for the posterior eigenmodes. The first four eigenmodes capture large-scale flow structures (appeared near the wall, as seen in Figs. 4(b)-4(e)), but the fiftieth eigenmode captures small-scale flow structures (as shown in Fig. 4(f)) because this eigenmode contains extremely little fluctuating energy. Besides, the structures captured by the first eigenmode are similar with those captured by the second eigenmode. Maybe, the containing energy in these two eigenmodes is almost the same (as shown in Table 2).
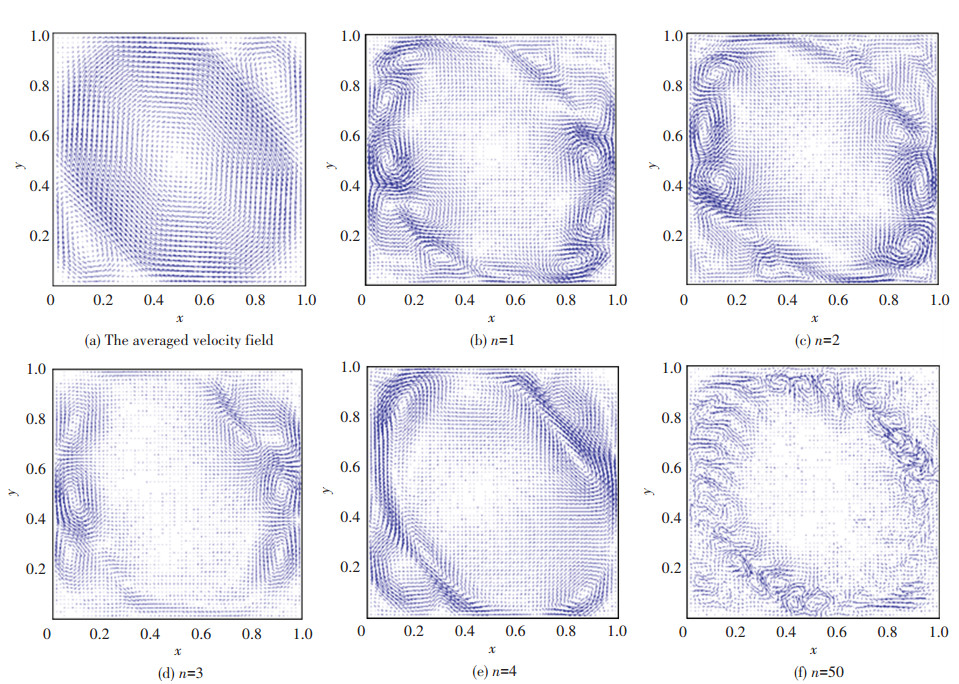
|
Figure 4 Vector plots of the averaged velocity field and 1st, 2nd, 3rd, 4th and 50th POD eigenmodes of fluctuating velocity field |
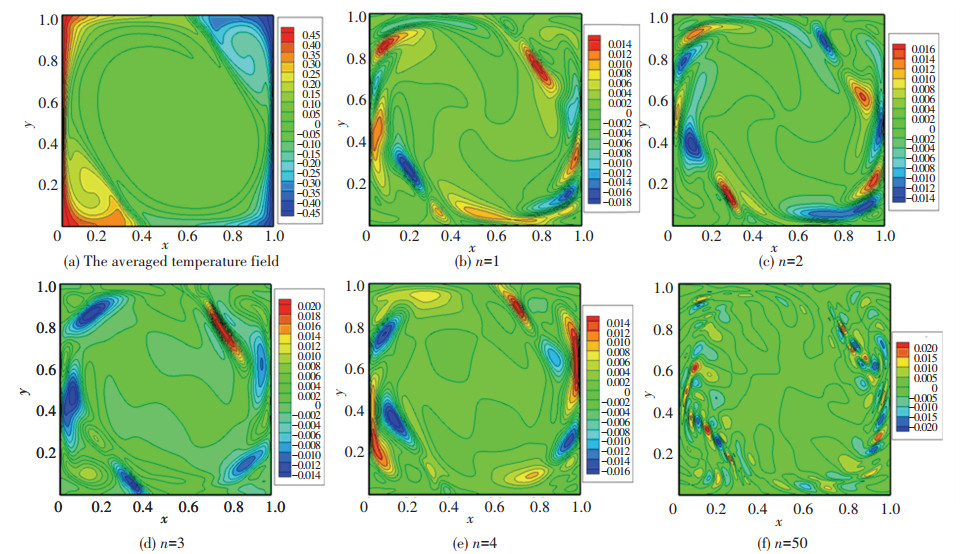
Similarly, we can also analyze the averaged temperature field and POD eigenmodes of temperature, as shown in Fig. 5.
|
Figure 5 Isothermal contours of the averaged temperature field and 1st, 2nd, 3rd, 4th and 50th POD eigenmodes of fluctuating temperature field |
From Fig. 5(a), the temperature in LSC structure is uniform, and the high and low temperature areas focus on the four corners. For POD eigenmodes of temperature, actually they represent the spatial plume structures. The first four eigenmodes extract large-scale plume structures near the wall (as shown in Figs. 5(b)-5(e)). However, the fiftieth eigenmode only extracts small-scale plume structures. Likewise, the plume structures captured by the first two eigenmodes are similar.
4 Low Dimensional Model for Rayleigh-Bénard Convection 4.1 Low-Dimension Model ProcedureWe want to construct low-dimensional model which can approximately represent the complex dynamical characteristics of original flow system. In the following, we derive the low-dimensional model for Rayleigh-Bénard convection by taking the inner product of the time derivatives of the rescaled fluctuation fields and the eigenmodes.
Firstly, the instantaneous velocity and instantaneous temperature can be written as:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{\bar u}}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{u'}}\left( {\mathit{\boldsymbol{x}},t} \right)\\ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{ \boldsymbol{\varTheta} '}}\left( {\mathit{\boldsymbol{x}},t} \right) \end{array} \right. $ | (20) |
where u(x) and Θ(x) are the averaged velocity and averaged temperature, respectively; u′(x, t) and Θ′(x, t) are the fluctuating velocity and fluctuating temperature, respectively. In LDM, the above POD eigenmodes (as obtained in Section 3.2) are used as a basis for a Galerkin projection of incompressible Navier-Stokes-Boussinesq equation and temperature equation. So the fluctuating velocity and fluctuating temperature can be expressed as:
| $ \mathit{\boldsymbol{u'}}\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{i = 1}^N {{a_i}\left( t \right){\mathit{\boldsymbol{\sigma }}_i}\left( \mathit{\boldsymbol{x}} \right)} $ | (21) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} '}}\left( {\mathit{\boldsymbol{x}},t} \right) = \sum\limits_{i = 1}^N {{b_i}\left( t \right){\theta _i}\left( \mathit{\boldsymbol{x}} \right)} $ | (22) |
where θi(x) is POD eigenmodes for fluctuating temperature field; bi(t) is the coefficient.
Since the POD eigenmodes satisfy the continuity equation, so it just needs to handle the momentum equation and temperature equation. So substituting Eq.(20) into Eq.(1) gives:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\frac{{\partial \mathit{\boldsymbol{u'}}}}{{\partial t}} + {{\mathit{\boldsymbol{\bar u}}}_j}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}}} + {{\bar u}_j}\frac{{\partial \mathit{\boldsymbol{u'}}}}{{\partial {x_j}}} + {{u'}_j}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}}} + {{u'}_j}\frac{{\partial \mathit{\boldsymbol{u'}}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + }\\ {{{\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)}^{1/2}}\frac{{{\partial ^2}\mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}\partial {x_j}}} + {{\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)}^{1/2}}\frac{{{\partial ^2}\mathit{\boldsymbol{u'}}}}{{\partial {x_j}\partial {x_j}}} + \mathit{\bar \Theta }{\delta _{i2}} + \mathit{\Theta '}{\delta _{i2}}} \end{array}\\ \begin{array}{*{20}{c}} {\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\varTheta} '}}}}{{\partial t}} + {{\bar u}_j}\frac{{\partial \mathit{\bar \Theta }}}{{\partial {x_j}}} + {{u'}_j}\frac{{\partial \mathit{\bar \Theta }}}{{\partial {x_j}}} + {{\bar u}_j}\frac{{\partial \mathit{\Theta '}}}{{\partial {x_j}}} + {{u'}_j}\frac{{\partial \mathit{\Theta '}}}{{\partial {x_j}}} = }\\ {\frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\frac{{{\partial ^2}\mathit{\bar \Theta }}}{{\partial {x_j}\partial {x_j}}} + \frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\frac{{{\partial ^2}\mathit{\Theta '}}}{{\partial {x_j}\partial {x_j}}}} \end{array} \end{array} \right. $ | (23) |
Substituting Eqs.(21) and (22) into Eq.(23) gives:
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^N {\frac{{{\rm{d}}{a_i}}}{{{\rm{d}}t}}{\mathit{\boldsymbol{\sigma }}_i}} + {{\bar u}_j}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}}} + \sum\limits_{j = 1}^N {{a_j}{\mathit{\boldsymbol{\sigma }}_{jl}}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_l}}}} + \sum\limits_{i = 1}^N {{a_i}{{\bar u}_j}\frac{{\partial {\mathit{\boldsymbol{\sigma }}_i}}}{{\partial {x_j}}}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{a_i}{a_j}{\sigma _{il}}\frac{{\partial {\mathit{\boldsymbol{\sigma }}_j}}}{{\partial {x_{il}}}}} } = - \frac{{\partial p}}{{\partial {x_i}}} + {\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\frac{{{\partial ^2}\mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}\partial {x_j}}} + \\ \;\;\;\;\;\;{\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\sum\limits_{i = 1}^N {{a_i}\frac{{{\partial ^2}{\mathit{\boldsymbol{\sigma }}_i}}}{{\partial {x_j}\partial {x_j}}}} + \mathit{\bar \Theta }{\delta _{i2}} + \sum\limits_{l = 1}^N {{b_l}{\theta _l}{\delta _{i2}}} \\ \sum\limits_{i = 1}^N {\frac{{{\rm{d}}{b_i}}}{{{\rm{d}}t}}{\theta _i}} + {{\bar u}_j}\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}}{{\partial {x_j}}} + \sum\limits_{j = 1}^N {{a_j}{\mathit{\boldsymbol{\sigma }}_{jl}}\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}}{{\partial {x_l}}}} + \sum\limits_{i = 1}^N {{b_i}{{\bar u}_j}\frac{{\partial {\theta _i}}}{{\partial {x_j}}}} + \\ \;\;\;\;\;\;\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{b_i}{a_j}{\sigma _{jl}}\frac{{\partial {\theta _i}}}{{\partial {x_l}}}} } = \frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\frac{{{\partial ^2}\mathit{\bar \Theta }}}{{\partial {x_j}\partial {x_j}}} + \\ \;\;\;\;\;\;{\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\sum\limits_{i = 1}^N {{b_i}\frac{{{\partial ^2}{\theta _i}}}{{\partial {x_j}\partial {x_j}}}} \end{array} \right. $ | (24) |
Projecting the first equation in Eq.(24) along σk and the second equation in Eq.(24) along θk ((σi, σj)=δij and (θi, θj)=δij) gives:
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}{a_k}}}{{{\rm{d}}t}} + {A^{kij}}{a_i}{a_j} + {B^{ki}}{a_i} + {C^k} + {D^{ki}}{b_i} = 0\\ \frac{{{\rm{d}}{b_k}}}{{{\rm{d}}t}} + {E^{kij}}{a_i}{b_j} + {F^{ki}}{a_i} + {J^{ki}}{b_i} + {H^k} = 0 \end{array} \right. $ | (25) |
where
| $ {A^{kij}} = \left( {{\sigma _{il}}\frac{{\partial {\mathit{\boldsymbol{\sigma }}_j}}}{{\partial {x_l}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) $ |
| $ {B^{ki}} = \left( {{\sigma _{il}}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_{il}}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) + \left( {{{\bar u}_j}\frac{{\partial {\mathit{\boldsymbol{\sigma }}_i}}}{{\partial {x_j}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) - {\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\left( {\frac{{{\partial ^2}{\mathit{\boldsymbol{\sigma }}_i}}}{{\partial {x_j}\partial {x_j}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) $ |
| $ {C^k} = \left( {{{\bar u}_j}\frac{{\partial \mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) - \left( {\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}{\delta _{i2}},{\mathit{\boldsymbol{\sigma }}_k}} \right) - {\left( {\frac{{\mathit{Pr}}}{{Ra}}} \right)^{1/2}}\left( {\frac{{{\partial ^2}\mathit{\boldsymbol{\bar u}}}}{{\partial {x_j}\partial {x_j}}},{\mathit{\boldsymbol{\sigma }}_k}} \right) $ |
| $ {D^{ki}} = \left( {{\theta _i}{\delta _{l2}},{\mathit{\boldsymbol{\sigma }}_k}} \right) $ |
| $ {E^{kij}} = \left( {{\mathit{\boldsymbol{\sigma }}_{il}}\frac{{\partial {\theta _j}}}{{\partial {x_l}}},{\theta _k}} \right) $ |
| $ {F^{ki}} = \left( {{\mathit{\boldsymbol{\sigma }}_{il}}\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}}{{\partial {x_{il}}}},{\theta _k}} \right) $ |
| $ {J^{ki}} = \left( {{{\bar u}_j}\frac{{\partial {\theta _i}}}{{\partial {x_j}}},{\theta _k}} \right) - \frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\left( {\frac{{{\partial ^2}{\theta _i}}}{{\partial {x_j}\partial {x_j}}},{\theta _k}} \right) $ |
| $ {H^k} = \left( {{{\bar u}_j}\frac{{\partial \mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}}{{\partial {x_j}}} - \frac{1}{{{{\left( {\mathit{Pr}Ra} \right)}^{1/2}}}}\frac{{{\partial ^2}\mathit{\boldsymbol{ \boldsymbol{\bar \varTheta} }}}}{{\partial {x_j}\partial {x_j}}},{\theta _k}} \right) $ |
We refer to this set (Eq.(25)) as the LDM based on POD-Galerkin.
In Eq.(25), the pressure term is omitted. Actually,
| $ \left( {{\mathit{\boldsymbol{\sigma }}_k}\left( \mathit{\boldsymbol{x}} \right),\nabla p} \right) = - \left( {{\rm{div}}{\mathit{\boldsymbol{\sigma }}_k}\left( x \right),p} \right) + \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{\sigma }}_k}\left( \mathit{\boldsymbol{x}} \right) \cdot \mathit{\boldsymbol{n}}p{\rm{d}}S} $ | (26) |
both terms on the right-hand side and left hand side are zero since the POD eigenmodes are divergence free and satisfies the (homogeneous) boundary condition.
Eq.(25) is an ordinary differential equation. To reduce the error between LDM and DNS, the same discretization used in DNS was adopted in solving Eq.(25).
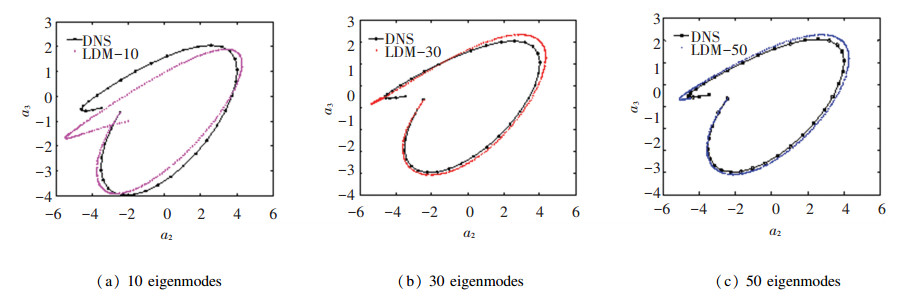
4.2 Phase Portraits AnalysisWe want to use a small number of POD eigenmodes in LDM (Eq.(25)) so as to reflect the original flow characteristics, because it is easy to calculate. In general, LDM should contain at least 90% of the total energy. From Table 2, it is found that 10 POD eigenmodes can extract 95.57% energy. For a comparison, we choose three different eigenmodes. Fig. 6 shows the phase portraits of velocity expansion coefficient obtained from DNS and LDM at different eigenmodes. It is clearly seen that LDM-10 can predict the short-time dynamical behavior but cannot predict long-time dynamical behavior as time evolves. Phase portraits are increasingly close to DNS as the number of eigenmodes used in LDM increase. That is to say, LDM-50 can preferably predict the original flow characteristics, but to point out that it is still difficult to use LDM-50 for long-time prediction, as discussed later. Besides, the time for LDM calculation remarkably increases with the increase of eigenmodes. It is proportional to the number of eigenmodes to the power 3.
|
Figure 6 Phase portraits of velocity expansion coefficient obtained from DNS and LDM at different eigenmodes |
Similarly, we analyze the phase portraits of temperature expansion coefficient obtained from DNS and LDM at different eigenmodes, as shown in Fig. 7. Compared with Fig. 6, it is found that the change trend is similar with that of velocity expansion coefficient. Although LDM-10 cannot accurately predict the temperature characteristics, it can give the rough trend for a short time. Besides, in the phase space (as shown in Figs. 6 and 7), there is no limit cycle or limit point. That is to say, the RB convection at Ra=107 is not stable or periodic.

|
Figure 7 Phase portraits of temperature expansion coefficient obtained from DNS and LDM at different eigenmodes |
4.3 The Prediction Results Based on LDM
In Section 4.2, it is shown that the phase portraits based on LDM-50 agree well with DNS. Whether it is suitable to predict the characteristics of flow filed and temperature field based on this model? We investigate the predicted streamline and isothermal for different time t=2, 9 and 15 based on LDM-50, as shown in Fig. 8. It is found that this model can predict well (i.e., a short-time prediction) compared with DNS results, but as time evolves, there exists the difference between LDM and DNS. That is to say, it is still difficult to long-time accurately predict the flow and temperature fields based on LDM-50, although 50 eigenmodes contain over 99% energy.

|
Figure 8 The comparison of streamline and isothermal between DNS and the predicted results based on LDM-50 for time t=2, 9 and 15 |
Table 3 lists the relative errors between DNS and LDM predicted by the first 50 eigenmodes at different times, and the definition of relative errors is shown in Eq.(27), where the subscript L and D represent the results of LDM and DNS.
| $ e\left( t \right)\% = \frac{{\left| {\left( {{\mathit{\boldsymbol{u}}_L}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{u}}_D}\left( {\mathit{\boldsymbol{x}},t} \right),{\mathit{\boldsymbol{u}}_L}\left( {\mathit{\boldsymbol{x}},t} \right) - {\mathit{\boldsymbol{u}}_D}\left( {\mathit{\boldsymbol{x}},t} \right)} \right)} \right|}}{{\left| {\left( {{\mathit{\boldsymbol{u}}_D}\left( {\mathit{\boldsymbol{x}},t} \right),{\mathit{\boldsymbol{u}}_D}\left( {\mathit{\boldsymbol{x}},t} \right)} \right)} \right|}} $ | (27) |
| Table 3 Relative errors of velocity between DNS and LDM of 50 eigenmodes |
From Table 3, it can be found that the error is relative small for a short-time prediction by POD-LDM, but as time evolves, the error becomes larger. That is to say, it is difficult for a long-time prediction based on POD-LDM.
5 Summary and OutlookWe have carried out direct numerical simulation for two-dimensional Rayleigh-Bénard convection in a Cartesian domain at Ra=107 and Pr=0.71. The POD eigenmodes have been obtained by a so-called snapshot method from 200 statistically independent realizations of RB convection. We have derived low-dimensional model based on POD-Galerkin for RB convection and make a preliminary prediction study based on LDM.
Our results can be summarized as follows. Through POD analysis, the results show that the first leading eigenmodes capture large-scale flow structures and large-scale plume structures, and only 10 eigenmodes can extract 95.57% fluctuating energy, even 50 eigenmodes can extract 99.98% fluctuating energy. These results offer strong proof for constructing LDM. Based on LDM with different truncated eigenmodes, the results show that the phase portraits obtained from LDM-50 agree well with DNS results. But it is still difficult to accurately predict long-time dynamical characteristics of original flow system based on LDM-50. Even though we use LDM with more eigenmodes (such as 200 eigenmodes), it is also difficult to long-time predict accurately. The reasons are as follows: (1) Turbulence is infinite-dimensional dynamical system, and finite-dimensional dynamical model based on POD-Galerkin is difficult to perfectly represent real turbulence; (2) LDM with the truncated eigenmodes does not include the interaction with the non-resolved eigenmodes, the LDM will not be able to dissipate enough energy. This is because the dissipation process takes places at the small-scale structures, which are depicted by high-order eigenmodes and most energy is extracted by large-scale structures, which are depicted by the first leading eigenmodes. Therefore, if using LDM with few truncated eigenmodes (saving much computational time) to predict the flow and temperature characteristics, it needs to model the energy transport to the non-resolved POD eigenmodes. This is our work in the future.
| [1] |
Lumley J L. The structure of inhomogeneous turbulent flows. In Yaglom A M, Tatarski V I, editors, Atmospheric Turbulence and Radio Wave Propagation. Nauka, 1967. 166-178.
( 0) 0)
|
| [2] |
Sirovich L. Turbulence and the dynamics of coherent structures. Ⅰ: coherent structures. Ⅱ: symmetries and transformations. Ⅲ: dynamics and scaling. Quarterly of Applied Mathematics, 1987, 45(3): 561-590. DOI:10.1090/qam/910463 ( 0) 0)
|
| [3] |
Sen M, Bhaganagar K, Juttijudata V. Application of proper orthogonal decomposition (POD) to investigate a turbulent boundary layer in a channel with rough walls. Journal of Turbulence, 2007, 8(41): 1-21. DOI:10.1080/14685240701615960 ( 0) 0)
|
| [4] |
Puragliesi R, Leriche E. Proper orthogonal decomposition of a fully confined cubical differentially heated cavity flow at Rayleigh number Ra=109. Computer & Fluids, 2012, 61: 14-20. DOI:10.1016/j.compfluid.2011.06.005 ( 0) 0)
|
| [5] |
Meyer K E, Pedersen J M, Özcan O. A turbulent jet in crossflow analysed with proper orthogonal decomposition. Journal of Fluid Mechanics, 2007, 583: 199-227. DOI:10.1017/S0022112007006143 ( 0) 0)
|
| [6] |
Rahal S, Cerisier P, Azuma H. Application of the proper orthogonal decomposition to turbulent convective flows in a simulated Czochralski system. International Journal of Heat and Mass Transfer, 2008, 51(17/18): 4216-4227. DOI:10.1016/j.ijheatmasstransfer.2008.01.021 ( 0) 0)
|
| [7] |
Wang Y, Yu B, Wu X. POD study on the mechanism of turbulent drag reduction and heat transfer reduction based on direct numerical simulation. Progress in Computational Fluid Dynamics, 2011, 11(3/4): 149-159. DOI:10.1504/PCFD.2011.041014 ( 0) 0)
|
| [8] |
Wang Y, Yu B, Wu X, et al. POD and wavelet analyses on the flow structures of a polymer drag-reducing flow based on DNS data. International Journal of Heat and Mass Transfer, 2012, 55(17/18): 4849-4861. DOI:10.1016/j.ijheatmasstransfer.2012.04.055 ( 0) 0)
|
| [9] |
Wang Y, Yu B, Wu X, et al. POD study on large-scale structures of viscoelastic turbulent drag-reducing flow. Advances in Mechanical Engineering, 2014, 24: Article ID 574381. DOI:10.1155/2014/574381 ( 0) 0)
|
| [10] |
Cazemier W, Verstappen R W C P, Veldman A E P. Proper orthogonal decomposition and low-dimensional models for driven cavity flows. Physics of Fluids, 1998, 10(7): 1685-1699. DOI:10.1063/1.869686 ( 0) 0)
|
| [11] |
Venturi D, Wan X L, Karniadakis G E. Stochastic bifurcation analysis of rayleigh-benard convection. Journal of Fluid Mechanics, 2010, 650: 391-413. DOI:10.1017/S0022112009993685 ( 0) 0)
|
| [12] |
Becker N, Ahlers G. Domain chaos puzzle and the calculation of the structure factor and its half-width. Physical Review E, 2006, 73(4): Article ID 046209. DOI:10.1103/PhysRevE.73.046209 ( 0) 0)
|
| [13] |
Noack B R, Eckelmann H. A low-dimensional Galerkin method for the three-dimensional flow around a circular cylinder. Physics of Fluids, 1994, 6(l): 124-143. DOI:10.1063/1.868433 ( 0) 0)
|
| [14] |
Aranson I, Assenheimer M, Steinberg V, et al. Large-scale flow and spiral core instability in Rayleigh-Benard convection. Physical Review E, 1997, 55(5): 4877-4880. DOI:10.1103/PhysRevE.55.R4877 ( 0) 0)
|
| [15] |
Ravindran S S. Adaptive reduced-order controllers for a thermal flow system using proper orthogonal decomposition. SIAM Journal on Scientific Computing, 2002, 23(6): 1924-1942. DOI:10.1137/S1064827500374716 ( 0) 0)
|
| [16] |
Prabhu R D, Collis S S, Chang Y. The influence of control on proper orthogonal decomposition of wall-bounded turbulent flows. Physics of Fluids, 2001, 13(2): 520-537. DOI:10.1063/1.1333038 ( 0) 0)
|
| [17] |
Bergmann M, Cordier L, Brancher J P. Optimal rotary control of the cylinder wake using proper orthogonal decomposition reduced-order model. Physics of Fluids, 2005, 17(9): Article ID 097101. DOI:10.1063/1.2033624 ( 0) 0)
|
| [18] |
Ravindran S S. A reduced-order approach for optimal control of fluids using proper orthogonal decomposition. International Journal of Numerical Method-Fluids, 2000, 34(5): 425-448. DOI:10.1002/1097-0363(20001115)34:5<425::AID-FLD67>3.0.CO;2-W ( 0) 0)
|
| [19] |
Aubry N, Holmes P, Lumley J L, et al. The dynamics of coherent structures in the wall region of a turbulent boundary layer. Journal of Fluid Mechanics, 1988, 192: 115-173. DOI:10.1017/S0022112088001818 ( 0) 0)
|
| [20] |
Berkooz G, Holmes P, Lumley J L. On the relation between low-dimensional models and the dynamics of coherent structures in the turbulent wall layer. Theoretical and Computational Fluid Dynamics, 1993, 4(4): 255-269. DOI:10.1007/BF00418776 ( 0) 0)
|
| [21] |
Noack B R, Afanasiev K, Morzynski M, et al. A hierarchy of low-dimensional models for the transient and post-transient cylinder wake. Journal of Fluid Mechanics, 2003, 497: 335-363. DOI:10.1017/S0022112003006694 ( 0) 0)
|
| [22] |
Iiak M, Rowley C W. Modeling of transitional channel flow using balanced proper orthogonal decomposition. Physics of Fluids, 2008, 20(3): Article ID 034103. DOI:10.1063/1.2840197 ( 0) 0)
|
| [23] |
Ma X, Karniadakis G E. A low-dimensional model for simulating three-dimensional cylinder flow. Journal of Fluid Mechanics, 2002, 458: 181-190. DOI:10.1017/S0022112002007991 ( 0) 0)
|
| [24] |
Smith T R, Moehlis J, Holmes P. Low-dimensional models for turbulent plane Couette flow in a minimal flow unit. Journal of Fluid Mechanics, 2005, 538: 71-110. DOI:10.1017/S0022112005005288 ( 0) 0)
|
| [25] |
Banerjee S, Cole J V, Jensen K F. Nonlinear model reduction strategies for rapid thermal processing systems. IEEE Transactions on Semiconductor Manufacturing, 1998, 11(2): 266-275. DOI:10.1109/66.670175 ( 0) 0)
|
| [26] |
Białecki R A, Kassab A J, Fic A. Proper orthogonal decomposition and modal analysis for acceleration of transient FEM thermal analysis. International Journal of Numerical Methods in Engineering, 2005, 62(6): 774-797. DOI:10.1002/nme.1205 ( 0) 0)
|
| [27] |
Wang Y, Yu B, Cao Z Z, et al. A comparative study of POD interpolation and POD projection methods for fast and accurate prediction of heat transfer problems. International Journal of Heat and Mass Transfer, 2012, 55(17/18): 4827-4836. DOI:10.1016/j.ijheatmasstransfer.2012.04.053 ( 0) 0)
|
| [28] |
Han D X, Yu B, Yu G J, et al. Study on a BFC-based POD-Galerkin ROM for the steady-state heat transfer problem. International Journal of Heat and Mass Transfer, 2014, 69: 1-5. DOI:10.1016/j.ijheatmasstransfer.2013.10.004 ( 0) 0)
|
| [29] |
Han D X, Yu B, Zhang X Y. Study on a BFC-based POD-Galerkin reduced-order model for the unsteady-state variable-property heat transfer problem. Numerical Heat Transfer, Part B: Fundamentals, 2014, 65(3): 256-281. DOI:10.1080/10407790.2013.849989 ( 0) 0)
|
| [30] |
Samadiani E, Joshi Y. Multi-parameter model reduction in multi-scale convection systems. International Journal of Heat and Mass Transfer, 2010, 53(9-10): 2193-2205. DOI:10.1016/j.ijheatmasstransfer.2009.12.013 ( 0) 0)
|
| [31] |
Selimefendigil F. Numerical analysis and POD based interpolation of mixed convection heat transfer in horizontal channel with cavity heated from below. Engineering Application of Computational Fluid Mechanics, 2013, 7(2): 261-271. DOI:10.1080/19942060.2013.11015469 ( 0) 0)
|
| [32] |
Bailon-Cuba J, Shishkina O, Wagner C, et al. Low-dimensional model of turbulent mixed convection in a complex domain. Physics of Fluids, 2012, 24(10): Article ID 107101. DOI:10.1063/1.4757228 ( 0) 0)
|
| [33] |
Tarman H I. A Karhunen-Loève-based approach to numerical simulation of transition in Rayleigh-Bènard convection. Numerical Heat Transfer, Part B, 2003, 43: 567-586. DOI:10.1080/10407790390122186 ( 0) 0)
|
| [34] |
Sirovich L, Park H. Turbulent thermal convection in a finite domain: Part Ⅰ : theory. Physics of Fluids A, 1990, 2(9): 1649-1658. DOI:10.1063/1.857572 ( 0) 0)
|
| [35] |
Park H, Sirovich L. Turbulent thermal convection in a finite domain: Part Ⅱ. Numerical results. Physics of Fluids A:Fluid Dynamics, 1990, 2(9): 1659-1668. DOI:10.1063/1.857573 ( 0) 0)
|
| [36] |
Deane A E, Sirovich L. A computational study of Rayleigh-Bénard convection. Part 1. Rayleigh number dependence. Journal of Fluid Mechanics, 1991, 222: 231-250. DOI:10.1017/S0022112091001088 ( 0) 0)
|
| [37] |
Sirovich L, Deane A E. A computational study of Rayleigh-Bénard convection. Part 2. Dimension considerations. Journal of Fluid Mechanics, 1991, 222: 251-265. DOI:10.1017/S002211209100109X ( 0) 0)
|
| [38] |
Tarman I H. An improved dynamical approximation to Boussinesq equation using Karhunen-Loève basis. Computer Methods in Applied Mechanics and Engineering, 1997, 144(1/2): 153-162. DOI:10.1016/S0045-7825(96)01166-8 ( 0) 0)
|
| [39] |
San O, Borggaard J. Basis selection and closure for POD models of convection dominated Boussinesq flows. Proceedings of the 21st International Symposium on Mathematical Theory of Networks and Systems. Groningen, 2014. 132-139.
( 0) 0)
|
| [40] |
Ahlers G, Grossmann S, Lohse D. Heat transfer and large scale dynamics in turbulent Rayleigh-Bénard convection. Reviews of Modern Physics, 2009, 81(2): 503-537. DOI:10.1103/RevModPhys.81.503 ( 0) 0)
|
| [41] |
Quertatani N, Cheikh N B, Beya B B, et al. Numerical simulation of two dimensional Rayleigh-Bénard convection in an enclosure. Comptes Rendus Mecanique, 2008, 336(5): 464-470. DOI:10.1016/j.crme.2008.02.004 ( 0) 0)
|
| [42] |
Turan O, Chakraborty N, Poole R J. Laminar Rayleigh-Bénard convection of yield stress fluids in a square enclosure. Journal of Non-Newtonian Fluid Mechanics, 2012, 171-172: 83-96. DOI:10.1016/j.jnnfm.2012.01.006 ( 0) 0)
|
| [43] |
Cai W H, Li F C, Zhang H N, et al. Study on the characteristics of turbulent drag-reducing channel flow by particle image velocimetry combining with proper orthogonal decomposition analysis. Physics of Fluids, 2009, 21(11): Article ID 115103. DOI:10.1063/1.3263706 ( 0) 0)
|
| [44] |
Meyer K E, Pedersen J M, Özcan O. A turbulent jet in crossflow analysed with proper orthogonal decomposition. Journal of Fluid Mechanics, 2007, 583: 199-227. DOI:10.1017/S0022112007006143 ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25


