2. Materials Chemistry, RWTH Aachen University, D-52074 Aachen, Germany
Li ion batteries (LIBs) are typical rechargeable batteries, in which Li ions move from the anode to the cathode during discharging, and then move back during charging. This cycling process is also known as the intercalation and deintercalation of Li ions. Compared to other rechargeable batteries, such as lead-acid, nickel-cadmium (Ni-Cd) and nickel-metal hydride (Ni-MH) batteries, LIBs have lower weight, higher energy density and a longer cycle life[1-3]. These excellent properties, as well as no memory effect and slow capacity loss, have made LIBs the most popular rechargeable batteries in the area of consumer electronics. People are using them every day and everywhere, such as in cell phones, laptops, cameras, etc. In recent years, LIBs are becoming more and more attractive in electric vehicles (EV). LIB is the most promising candidate for plug-in hybrid electric vehicles (PHEV) or plug-in electric vehicles (PEV) because of high energy density and low weight. However, further research is still necessary to keep them as safe as possible and their cost as low as possible[2-5].
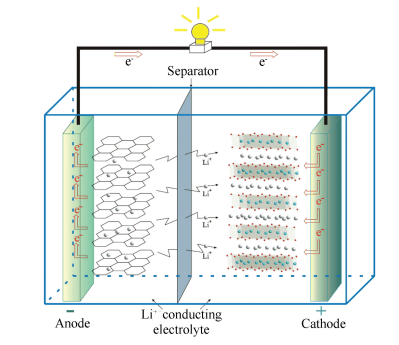
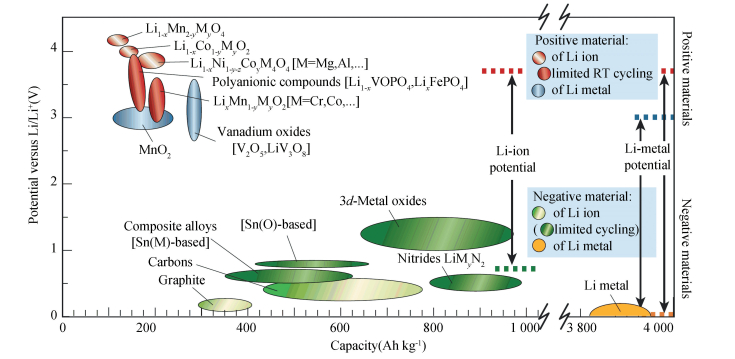
Three key functional components of a LIB are the cathode, the anode and the electrolyte. Graphite is presently the most popular anode. The lithium transition metal oxides, which possess high operating voltage, good reversibility and high capacity, are the most favored cathodes[1-5]. The electrolyte is usually a lithium salt in an organic non-aqueous solvent[1], such as lithium hexafluorophosphate (LiPF6) and lithium perchlorate (LiClO4). Fig. 1 shows a schematic diagram of a typical Li ion cell, which is composed of a layered structural LiMO2 (M = transition metal) cathode and a graphite anode[6].During the discharging process, Li ions are extracted from the anode host, move through the electrolyte and then intercalate into the cathode host. At the same time, electrons move from the anode to the cathode, which can be seen as electric current. This process is reversed during charging. The reaction of the whole LIB can be written as Cn + LiMO2 ↔ CnLix + Li1-xMO2. During the cycling, a number of chemical reactions take place in the cathodes. This leads to significant changes in the microstructure of the material. Phase diagrams are powerful tools to help understand these chemical reactions[6-7]. There are various material systems being used or promising as future electrode materials for LIBs[2], as shown in Fig. 2, which are interesting for researchers to study their phase equilibria, thermodynamic and electrochemical properties.
|
Figure 1 Schematic diagram of a Li ion cell(the arrows show the discharging process, Electron and Li+ move during charging in reverse directions[6]) |
|
Figure 2 Voltage versus capacity for positive-and negative-electrode materials (cathode and anode materials) presently used or under serious considerations for the next generation of rechargeable LIBs[2] |
At present, research of LIBs is focusing on lower cost, lower capacity loss, longer lifetime, higher energy density, higher stability and inherent safety. However, none of the present electrode materials is practically able to attain all these goals simultaneously[1-3]. Thus, the choice of certain electrode materials for a LIB is a compromise. Depending on the choices of materials, the voltage, capacity, life and safety of a LIB can be changed significantly. The very first step to design new electrode materials is to study its voltage and capacity, which can theoretically be predicted[6-14].
2 Cathode Materials and Theoretical Study in the LiteratureUsually, the cathode is the most expensive part with the highest weight among the three key components in a LIB[1, 7]. Also, properties of the cathode specially affect the performance of the entire LIB. Lithium-transition metal oxides as cathodes have extensively been investigated. Typical examples are lithium cobalt oxide (such as LiCoO2) with a layered structure, lithium iron phosphate (LiFePO4) with an olivine structure and lithium manganese oxide (such as LiMn2O4) with a spinel structure[1-3, 7]. The theoretical specific capacities of LiCoO2, LiFePO4, and LiMn2O4 are 273, 170 and 297 mAh/g, respectively[8]. All of them have some disadvantages. LiCoO2 has a relatively high cost and safety problems; LiFePO4 exhibits a poor electronic conductivity; LiMn2O4 suffers from the Jahn-Teller distortion with a large volume change of the cathode, which leads to capacity drop of the battery. Recently, the Li(Co, M)O2 cathodes (M = transition metals), e.g. Li(Co, Ni, Mn)O2, have been developed to improve the properties of LiCoO2. The Li(Co, M)O2 cathodes are, however, less stable in comparison with the spinel structure. The thermal decomposition already occurs at low temperatures[6]. Such kind of phase transformations can also be explained by phase diagrams[7].
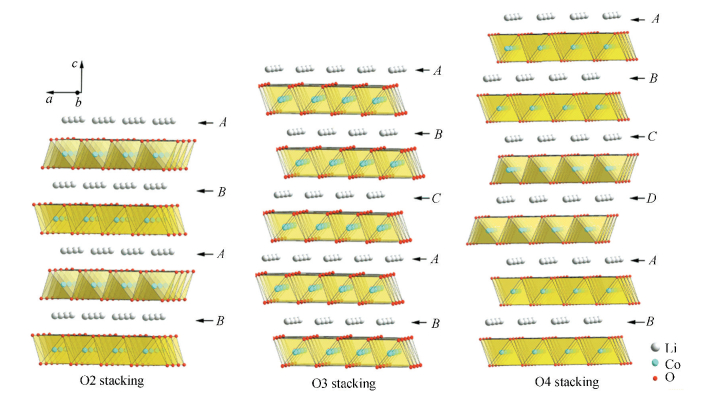
Information on the phase equilibria and thermodynamic properties of the Li-M-O (M = transition metal) system is of great importance. The CALPHAD approach can help to establish a thermodynamic database for multi-component Li-containing oxide systems. Lithium cobalt oxides and lithium nickel oxides have been used as quite popular cathodes[1-5]. All the possible cathodes based on the Li-(Co, Ni)-O system are of great interest to study their phase equilibria, thermodynamic and electrochemical properties. LiCoO2 has three types of layered structures: O2, O3 and O4. The letter (O) indicates the Li ion site (octahedral) and the number (2, 3 or 4) denotes the number of slabs within the hexagonal phases[15]. The three different structures can be distinguished by the types of Li stacking (or oxygen packing). All of them consist of CoO6 octahedra interleaved with Li ions[6], as shown in Fig. 3. The layered structures facilitate intercalation and deintercalation of Li ions. Among the O2, O3 and O4 structures, O3-LiCoO2 with the space group R 3m is the most stable one, which is widely used in LIBs[1-3]. The O2-LiCoO2 and O4-LiCoO2 phases, both with the space group P63mc, are suggested to be good candidates as cathodes in LIBs[15-17].The cell voltage and capacity of Li/O4-LiCoO2 is quite similar to that of Li/O3-LiCoO2, but with absence of structural transformations[16]. The relatively high cost and safety problems, which are associated with electrolyte oxidation during prolonged cycling, limit the applications of O3-LiCoO2 in industry[2, 18-19]. As a replacement of LiCoO2, LiNiO2 (also with the O3 structure) is one of the attractive candidates[2, 20-22]. However, the stoichoimetric LiNiO2 is very difficult to synthesize due to its lower thermodynamic stability compared to LiCoO2[23] and the presence of excess nickel on Li sites[24-25]. These anti sites in LiNiO2 strongly affect the capacity of the batteries[2, 20-21]. Li(Co, Ni)O2 with the O3 structure, as the solid solution between LiCoO2 and LiNiO2, has been developed to alleviate the drawbacks of LiCoO2 and LiNiO2[22, 24-26].
|
Figure 3 Crystal structures of LiCoO2 with different stacking of Li layers[6] |
The theoretical approaches based on first-principles calculations and empirical methods are the very first step to study the thermodynamic properties of metal oxides. These simple thermodynamic models can help to determine the Gibbs energy functions of the binary and ternary oxides in the Li-(Co, Ni)-O system[14]. Then, using the CALPHAD approach, the reliable Gibbs energy functions can be obtained, which can be used to calculate the phase equilibria and predict the cell voltages of LIBs[6, 27-32]. Therefore, it is important to apply the CALPHAD approach integrated with first-principles calculations and other theoretical methods, which can not only provide reliable phase equilibria and thermodynamic data for Lithium-transition metal oxides, but also predict the cell voltages of LIBs reasonably[6, 27-32]. The cell voltage (V) of a Li ion cell can be calculated using the following equation:
| $ V = - \frac{{\mu _{{\rm{Li}}}^{{\rm{Cathode}}} - \mu _{{\rm{Li}}}^{{\rm{Anode}}}}}{{zF}} $ | (1) |
where μLi is the Li chemical potential (which can directly be calculated with the Gibbs energy functions using the CALPHAD approach), z is the moles of electrons involved (for Li+, z=1), and F is Faraday's constant. The cell voltage of a Li/Li+ cell can be expressed as follows:
| $ V = - \frac{{\mu _{{\rm{Li}}}^{{\rm{Cathode}}}}}{F} $ | (2) |
The theoretical specific capacity of a cell can be calculated by Faraday's law, where the number of charge carrier (or the amount of Li) and the weight of the active material used in the electrode are the key parameters. Therefore, one can predict the theoretical specific capacity from the phase diagram by calculating the amount of lithium that can be intercalated in or deintercalated from the electrode. In reality, the practical specific capacity of an operating cell can be lower than the theoretical one. The reason is that not all Li can be removed from the lattice of the host material[7].
3 Anode Materials and Literature ReviewGraphite is the most widely used anode in LIBs owing to its abundance, long cycle time and low cost. However, the graphite anode exhibits a comparatively low energy density and has safety issues related to lithium deposition. Li-Metal systems have extensively been investigated as potential alternatives to graphite anodes, such as the Si-containing systems[33], the Li-Sb[34] and Li-Sn[35] systems. Literature review on the phase equilibria and thermodynamic data of Li-Sb and Li-Sn are presented as follows.
The Li-Sb system was firstly critically evaluated by Sangster and Pelton[36] based on the experimental work from Brauer et al.[37] and Weppner et al.[38] The melting temperature was considered to be in the range of 1 150 to 1 300 ℃ measured by Brauer and Zintl[37] and higher than 950 ℃ reported by Lebeau[39]. The αLi3Sb phase transforms to βLi3Sb at a temperature above 650 ℃ measured by Brauer and Zintl[37]. Three binary compounds were presented in the assessed phase diagram[36], viz.Li2Sb, αLi3Sb and βLi3Sb (high temperature phase). Then Fedorov[40] proposed a different phase diagram based on thermal analysis with the unannealed alloys and two additional compounds Li3Sb2 and LiSb2 were included. Recently, Kane et al.[41] determined the Li-Sb system using the electromotive force (EMF) measurement, but neither Li3Sb2 nor LiSb2 was confirmed to be stable. In their work, the eutectic temperature of L→(Sb)+Li2Sb was measured to be 460 ℃ and Li2Sb was formed by the peritectic reaction at a temperature of 584 ℃. In addition, the eutectic point was considered to be about 40 at.% Li. Based on the X-ray diffraction measurement (XRD) and electron probe microanalyses (EPMA) results, Zhang et al.[34] confirmed the Li-Sb phase diagram reported by Kane et al.[41] Enthalpies of formation of the Li3Sb and Li2Sb phases have been investigated by many authors[42-46]. Shchukarev et al.[43] and Kubaschewski and Catterall[44] determined the enthalpies of formation of Li3Sb using solution calorimetry (SC) and direct reaction calorimetry (DRC), respectively. In addition, Nikitin et al.[45] and Weppner and Huggins[38] measured the enthalpies of formation of the Li3Sb and Li2Sb phases by the cathodic polarization technique (CP) and EMF, respectively. Their experimental data are close to each other and inconsistent with the work of Shchukarev et al.[43] and Kubaschewski and Catterall[44]. Recently, Terlicka et al.[46] have determined the formation energies of Li3Sb and Li2Sb using the DRC technique, which are similar with the data reported by Nikitin et al.[45] and Weppner and Huggins[38]. Thermodynamic properties of the liquid Li-Sb alloys were investigated by two groups[41, 46]. Kane et al.[41] measured the thermodynamic properties of the Li-Sb alloys by EMF technique with the temperature ranges of 425-775 ℃ and composition ranges of 1-75 at.% Li. And Terlicka et al.[46] determined partial and integral mixing enthalpy of the liquid Li-Sb alloys at 820 K, 942 K, 922 K and 1 024 K by drop calorimetry. The thermodynamic data reported by Kane et al.[41], Weppner and Huggins[38], Nikitin et al.[45] and Terlicka et al.[46] are agreement with each other and accepted in this work.
Using the coulometric titrations at 415 ℃ and 25 ℃, Huggins[47-48] have determined the Li2Sn5, LiSn, Li7Sn3, Li5Sn2, Li13Sn5, Li7Sn2 and Li22Sn5 (or Li17Sn4) phases in the Li-Sn system. These investigations were consistent with the Li-Sn phase diagram[49-50]. However, under practical charging condition and/or at room temperature, it was found that only the lithium-poor phases Li2Sn5 and LiSn could be clearly distinguished[51-53], which suggested that the lithium-rich phases could not form long-range ordered structures due to the low mobility at room temperature and the huge volume change. The equilibrium open-circuit voltage has been reported using theoretical calculations[54-55], which agree well with the experimental data.
4 The CALPHAD ApproachThe CALPHAD approach has been proved to be a powerful tool to evaluate Gibbs free energy, predict multi-component phase diagrams and help to design new materials. CALPHAD stands for CALculation of PHAse Diagrams and is better defined by the subtitle of the CALPHAD journal (Computer Coupling of Phase Diagrams and Thermochemistry). The phase diagram, usually a diagram with axes for temperature and composition of a chemical system, consists of a number of phase-boundaries separating regions of temperature-and composition-space in which different phases are stable at equilibrium. The CALPHAD approach is based on the fact that equilibrium phase diagram of a system is a manifestation of its thermodynamic properties[56]. The thermodynamic properties of the system are the sum of the properties of the individual phases, including Gibbs energy, enthalpy, entropy, heat capacity, etc. Within the CALPHAD approach, one describes the thermodynamic properties of each phase with a mathematical model containing adjustable parameters. By determining the thermodynamic properties of all the phases in a system, the phase diagram can be constructed by calculation[56-57], which can be performed using the POLY-3 module within the Thermo-Calc software[58].
Fig. 4 shows the flow chart of the CALPHAD approach[57]. Firstly, reliable thermodynamic and phase equilibria data are necessary as input parameters, which can stem from experiments, theoretical calculations or estimation. Secondly, appropriate thermodynamic models are used for individual phases. Thirdly, adjustable thermodynamic parameters are introduced and then optimized considering all the reliable data. The above steps are known as the process of "thermodynamic optimization". This process can be achieved using the PARROT module within the Thermo-Calc software[58], which works by minimizing the square sum of the differences between measured and calculated values.

|
Figure 4 The flow chart of the CALPHAD approach[57] |
The obtained parameters from the "thermodynamic optimization" process together with parameters of pure elements generate the thermodynamic dataset of a system. The phase diagram can be calculated, while the unknown phase equilibria and thermodynamic properties can be predicted. The applications of the CALPHAD calculations can save large amounts of experimental work and make predictions available for multi-component systems.
From Fig. 4, it can be concluded that the accuracy of thermodynamic databases is most important for applications of the CALPHAD approach. This in turn suggests that reliable thermodynamic parameters and appropriate thermodynamic models are prerequisite[59-60]. Accurate Gibbs energy functions of individual phases are essential to get the correct phase diagram. It is also important, for cathodes in LIBs, to predict the cell voltages and study the electrochemical properties of batteries.
4.1 Thermodynamic Models Used in the CALPHAD ApproachIn the binary Li-O system, four phases, i.e. liquid, Li2O, Li2O2 and gas, are modeled using appropriate sublattice models[61]. Two lithium oxides (Li2O and Li2O2), which have been considered as stoichiometric compounds, are taken as examples. They are modeled using the following expression[61]:
| $ \begin{array}{*{20}{c}} {{}^oG_{{\rm{L}}{{\rm{i}}^{1 + }}:{{\rm{O}}^{2 - }}}^{{\rm{L}}{{\rm{i}}_2}{{\rm{O}}_n}} - 2H_{{\rm{Li}}}^{{\rm{SER}}} - nH_{\rm{O}}^{{\rm{SER}}} = A + B \cdot T + }\\ {C \cdot T \cdot \ln T + D \cdot {T^2} + F \cdot {T^{ - 1}}} \end{array} $ | (3) |
where the coefficients C, D, and F, are obtained from the expression of heat capacity for solid Li2On (n=1, 2).
Four phases, i.e. O3, O3' (ordered O3, also known as the monoclinic phase), H1-3 and O1, are modeled[6, 31] in the Li-(Co, Ni)-O system. Considering the order-disorder transition, a four-sublattice model is applied to describe both the O3 and O3' phases, written as (Li, Va)1/2(Li, Va)1/2(M)1(O)2 (M = Co, Ni)[6, 31]. In the disordered state, the first sublattice and the second one are identical, thus it is (Li, Va)1(M)1(O)2. The Gibbs energy of both the ordered and disordered states can be expressed as follows:
| $ G_m^{{\rm{Ord}}} = G_m^{{\rm{Dis}}}\left( {{x_i}} \right) + G_m^{{\rm{Ord}}}\left( {y_i^s} \right) - G_m^{{\rm{Ord}}}\left( {y_i^s = {x_i}} \right) $ | (4) |
where GmDis denotes the Gibbs energy of the disordered phase. GmOrd(yis)-GmOrd(yis=xi) denotes the contribution of the ordered phase to the Gibbs energy and is equal to 0 when the disordered O3 phase is stable.
The Gibbs energy for the disordered O3 phase is as follows:
| $ \begin{array}{l} G_m^{{\rm{Dis}}} = {x_{{\rm{Li}}}} \cdot G_m^{{\rm{O3 - LiM}}{{\rm{O}}_{\rm{2}}}} + {x_{{\rm{Va}}}} \cdot G_m^{{\rm{O3 - M}}{{\rm{O}}_{\rm{2}}}} + RT\left( {{x_{{\rm{Li}}}} \cdot } \right.\\ \;\;\;\;\;\;\;\left. {\ln {x_{{\rm{Li}}}} + {x_{{\rm{Va}}}} \cdot \ln {x_{{\rm{Va}}}}} \right) + {x_{{\rm{Li}}}} \cdot {x_{{\rm{Va}}}} \cdot \\ \;\;\;\;\;\;\;\;\sum\limits_{n = 0}^N {{}^nL_{{\rm{Li}},{\rm{Va:Co:O}}}^{{\rm{Dis}}}{{\left( {{x_{{\rm{Li}}}} - {x_{{\rm{Va}}}}} \right)}^i}} \end{array} $ | (5) |
where GO3-LiCoO2m and GO3-CoO2m are the Gibbs energy of the O3-LixMO2 phase at x= 1 and x = 0, respectively. xLi and xVa denote the mole fractions of Li and Va, respectively. R is the gas constant.
Considering the experimental heat capacity data, O3-LiCoO2 is modeled using the following expression[31]:
| $ \begin{array}{*{20}{c}} {{}^oG_m^{{\rm{O3 - LiCo}}{{\rm{O}}_{\rm{2}}}} - H_{{\rm{Li}}}^{{\rm{SER}}} - H_{{\rm{Co}}}^{{\rm{SER}}} - 2H_{\rm{O}}^{{\rm{SER}}} = A + B \cdot T + }\\ {C \cdot T \cdot \ln T + D \cdot {T^2} + E \cdot {T^{ - 1}}} \end{array} $ | (6) |
where A and B are parameters to be optimized, the coefficients C, D and E, are obtained from the expression of heat capacity for O3-LiCoO2. The Neumann-Kopp rule is applied to describe O3-CoO2, O3-LiNiO2 and O3-NiO2 because no heat capacity data above 298 K are available[6, 31].
GmOrd(yis) in Eq.(4) can be represented as follows:
| $ \begin{array}{l} G_m^{{\rm{Ord}}}\left( {y_i^s} \right) = \sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {\sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {{{y'}_i}y{''}_i^0G_{i:j:{\rm{M}}:{\rm{O}}}^{{\rm{Ord}}}} } + 1/2 \cdot RT\left( {\sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {{{y'}_i} \cdot \ln {{y'}_i}} + } \right.\\ \;\;\;\;\;\;\;\left. {\sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {{{y''}_i} \cdot \ln {{y''}_i}} } \right) + {{y'}_{{\rm{Li}}}} \cdot {{y'}_{{\rm{Va}}}} \cdot \sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {{{y''}_i} \cdot {}^0L_{{\rm{Li}},{\rm{Va:}}i{\rm{:M:O}}}^{{\rm{Ord}}}} + {{y''}_{{\rm{Li}}}} \cdot \\ \;\;\;\;\;\;\;{{y''}_{{\rm{Va}}}} \cdot \sum\limits_{i = {\rm{Li}}}^{{\rm{Va}}} {{{y'}_i} \cdot {}^0L_{i:{\rm{Li}},{\rm{Va:M:O}}}^{{\rm{Ord}}}} + {{y'}_{{\rm{Li}}}} \cdot {{y'}_{{\rm{Va}}}} \cdot {{y''}_{{\rm{Li}}}} \cdot {{y''}_{{\rm{Va}}}} \cdot \\ \;\;\;\;\;\;\;{}^0L_{{\rm{Li}},{\rm{Va:Li,Va}}:{\rm{M:O}}}^{{\rm{Ord}}} \end{array} $ | (7) |
where 0Gi:j:M:OOrd, yim, L are the Gibbs energy of the corresponding end-members, lattice fraction of the m-th sublattice, the interaction parameter, respectively.
4.2 Integrating First-Principles CalculationsIn the past decades, density functional theory (DFT) based first-principles calculations has played an important role in both the fundamental and applied research. The method has become one of the most popular and reliable methods for computational physics, chemistry and materials science[6-14, 27-29, 61-63]. The calculations are performed with atomistic detail by solving the Kohn-Sham equation, which could allow researchers to obtain the composition-structure-property relationships of matter without experimental data. Thermodynamic data are essential not only to better understand the properties of the cathodes in LIBs, but also to provide important input for the CALPHAD approach. When experimental information is scarce or completely lacking, it is necessary to obtain the data by first-principles calculations or empirical methods. It has been demonstrated that first-principles calculations provide a successful way of predicting the thermodynamic data for a wide range of materials[64-69], such as metallic compounds, metal carbides, etc. first-principles calculations are usually carried out using pure DFT, as implemented in the Vienna first-principles simulation package (VASP)[70-71]. Spin polarization effects are included when magnetic contributions to the total energy are significant.
4.3 Integrating Empirical MethodsConsidering the absence of experimental data and reliable calculations, it is necessary to estimate the entropies of metal oxides by empirical methods. The estimation of standard entropy data of inorganic compounds[72-75] shows reasonable agreement with the experimental results. The entropies of formation for the oxides can thus be obtained using empirical methods, which are used to determine the Gibbs energy functions for the oxides in the CALPHAD approach. The entropy data obtained for the Li-transition metal oxide, LixMyOz (M=Co, Ni) can be expressed as follows[14, 72]:
| $ \begin{array}{l} \Delta {\rm{S}}\left( {{\rm{L}}{{\rm{i}}_x}{{\rm{M}}_y}{{\rm{O}}_z}} \right) = S\left( {{\rm{L}}{{\rm{i}}_x}{{\rm{M}}_y}{{\rm{O}}_z}} \right) - \left[ {{x_{{\rm{Li}}}}S\left( {{\rm{Li}}} \right) + {x_{{\rm{Co}}}} \cdot } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {S\left( {\rm{M}} \right) + 0.5 \cdot {x_{\rm{O}}} \cdot S\left( {{{\rm{O}}_2}} \right)} \right] \end{array} $ | (8) |
where S(Li), S(M) and S(O2) denote the standard entropies of Li, M and O2 in the reference states, respectively.
A combination of the CALPHAD approach, first-principles calculations and empirical method has been applied to study the phase equilibria, thermodynamic and electrochemical properties of the Li-(Co, Ni)-O system as cathode materials in LIBs[6, 29-31].
4.4 Examples 4.4.1 The Li-O systemThe thermodynamic data[76-89] have been considered in the modeling[61]. The formation enthalpy data for Li2O from experiments and first-principles calculations[14] are consistent with each other. The fusion enthalpy of Li2O was estimated to be 58.576 kJ/mol. The enthalpy of formation for Li2O2, -632.62 and -605.9 kJ/mol, were determined using solution calorimetry. A value of -673.5 kJ/mol was obtained by first-principles calculations[14]. The experimental heat capacities of Li2O and Li2O2 can well be reproduced by the CALPHAD approach[61], as shown in Fig. 5.
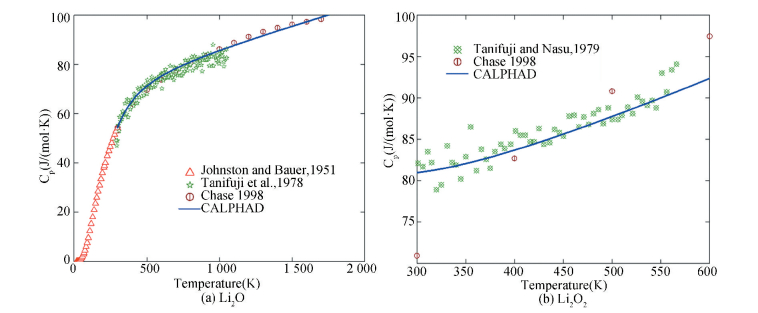
|
Figure 5 Heat capacity data of Li2O and Li2O2[61] |
Five stable phases at temperatures above 298 K, i.e. (Li), Li2O, Li2O2, liquid and gas phases, are considered in the thermodynamic modeling[61]. The equilibria between the liquid phase and solid Li2O have been investigated and the solubility of O in liquid over temperature range 468-1 007 K has been well determined[77]. Sangster and Pelton[76] reviewed the literature data[90-103] and reported an eutectic reaction involving (Li), Li2O and liquid at 453.6 K. The melting point of Li2O remains uncertain[61, 76]. Li2O2 decomposes into Li2O and O2 on heating at 613 K.
Considering all the experimental data, the Li-O phase diagram including the gas phase at 1 bar total pressure has been calculated using the CALPHAD approach[61], which is shown in Fig. 6. This is the first Li-O phase diagram ever obtained. The calculated thermodynamic properties and phase equilibria agree reasonably with the literature information and the first-principles data[61]. A set of self-consistent thermodynamic parameters for the Li-O system was obtained for modeling of further multi-component Li-containing oxide systems[6, 30-32].
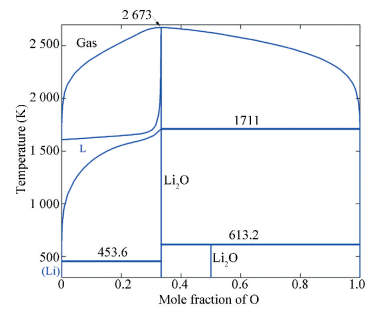
|
Figure 6 Calculated Li-O phase diagram including the gas phase at 1 bar total pressure[61] |
4.4.2 The Li-Co-O system
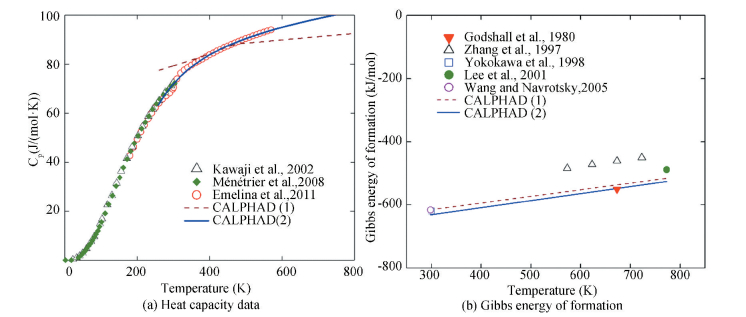
Abe and Koyama[30] and Chang et al.[31] have performed thermodynamic modeling of the Li-Co-O system using the CALPHAD approach. Five phases, i.e. O3, O3(Ⅱ), O3'(ordered O3, also known as the monoclinic phase), H1-3 and O1, have been detected by experiments[21-23, 104-108]. The O3(Ⅱ) phase comes from the insulator-metal transition of the O3 phase (the Li-rich O3 is an insulator). Due to lack of thermodynamic information and appropriate model, these two phases are considered as the same O3 phase[31]. In the thermodynamic modeling, only four phases (O3, O3', H-13 and O1) are considered and their structural data are summarized by Abe and Koyama in Ref.[30]. Using the obtained thermodynamic description, thermodynamic properties can be calculated and compared with the literature data[30-31]. The experimental heat capacity data of O3-LiCoO2 can be well described using the model[31]other than the Neumann-Kopp rule[30], as shown in Fig. 7(a). Fig. 7(b) shows the calculated Gibbs energy of formation for O3-LiCoO2 compared with literature data. Both the CALPHAD calculations agree well with the experimental data[30-31].
The calculated phase diagrams of the O3 structural LiCoO2-CoO2 system together with the experimental data is presented in Fig. 8. and The dotted lines indicate the order-disorder transition The CALPHAD result from Abe and Koyama[30] is shown in Fig. 8(a), which overestimates the order-disorder transition temperature and presents a wide range of the ordered phase. Compared with Ref.[30], the work by Chang et al.[31] can describe the experimental order-disorder transition perfectly, as shown in Fig. 8(b).
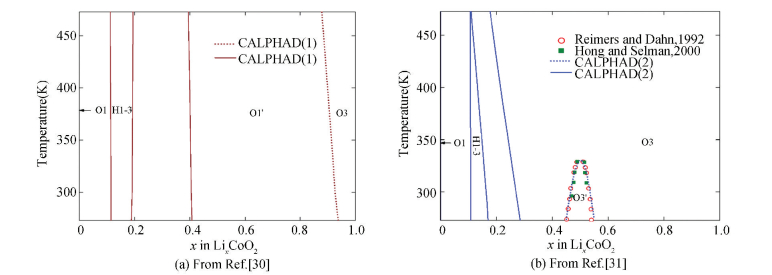
|
Figure 8 Phase diagrams of the O3 structural LiCoO2-CoO2 pseudo-binary system(The dotted lines indicate the order-disorder transition) |
The calculated cell voltage of Li/O3-LixCoO2(0≤x≤1) at 300 K using the CALPHAD approach[30-31] is shown in Fig. 9. The calculations can reproduce the experimental data quite well.
4.4.3 The Li-Ni-O system
During cycling of the Li/O3-LiNiO2 cell, four different phases are detected in the LiNiO2-NiO2 pseudo-binary system, i.e., O1, H1-3, O3 and O3' (ordered O3) [21, 25, 109-116]. For the O3-LiNiO2 phase, the heat capacity data below 300 K have been determined by Wang and Navrotsky[23] using drop solution calorimetry. A term, -7.16·T·ln(T), is added for O3-LiNiO2 in order to adjust the heat capacity data at 298 K[6].The calculated heat capacity of O3-LiNiO2 together with experimental data[6] is shown in Fig. 10(a). Fig. 10(b) shows the calculated enthalpies of formation for O3-LixNiO2 (0 < x < 1) relative to O3-NiO2 and O3-LiNiO2, which agree well with the first-principles data[6].
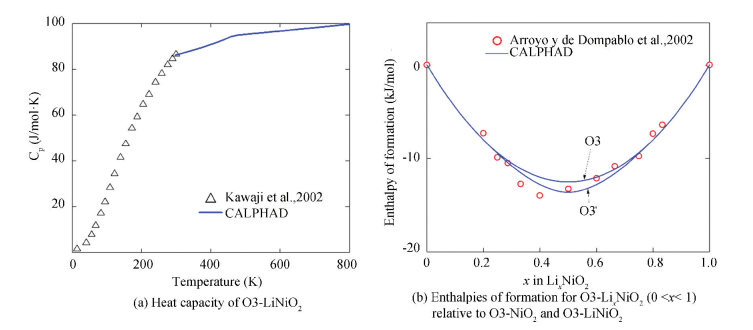
|
Figure 10 Calculated thermodynamic properties compared with the literature data[6] |
The calculated LiNiO2-NiO2 pseudo-binary phase diagram below 450 K is shown in Fig. 11(a)[6]. The literature shows that the symmetry of the disordered phase is maintained as the Li/O3-LixNiO2 (0 ≤ x ≤ 1) cell is charged to x = 0.75[6]. At elevated temperatures, the ordered O3 phase transforms into the disordered O3 phase[6].They are well reproduced by the CALPHAD results. The transformation temperature is found to be 383-413 K for Li0.5Ni1.02O2 and 393-413 K for Li0.52NiO2, respectively. The phase diagrams at 298 K are shown in Fig. 11(b)[6]. At x < 0.5, some controversies about the phase diagram exist. The single H1-3 phase region has been reported at x = 0.25-0.45, 0.15-0.35, 0.31-0.43 and 0.22-0.29[6]. Compared with the experiments, the calculated phase diagram is quite reasonable[6].
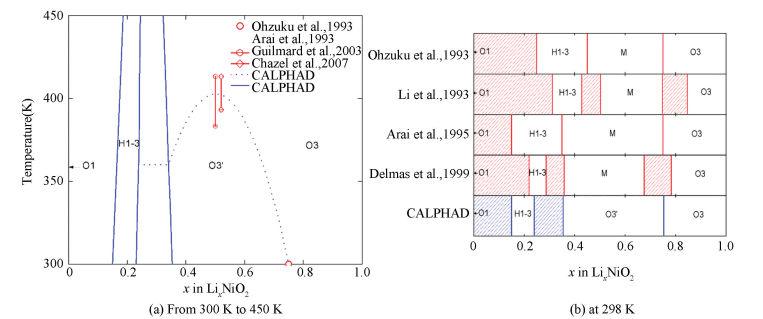
|
Figure 11 Phase diagram of the LiNiO2-NiO2 pseudo-binary system[6] |
The calculated cell voltage of Li/O3-LixNiO2(0≤ x ≤ 1) at 300 K is shown in Fig. 12, which is consistent with the experimental data[6].
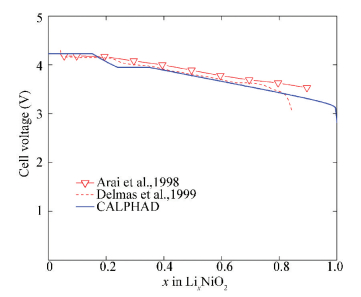
|
Figure 12 Cell voltages of Li/O3-LixNiO2 (0 ≤x≤ 1) at 300 K[6] |
4.4.4 The Li-(Co, Ni)-O system
Fig. 13(a) shows the variation of the lattice parameters and c/a ratio (both first-principles calculated and experimental results[21-25, 115-119]) versus y in the O3-LiCoyNi1-yO2 solid solution. It is clearly seen from Fig. 13(a) that both a and c decrease almost linearly with increasing Co content. At the same time, the c/a ratio increases almost linearly with increasing Co content, suggesting that substitution of Co/Ni increases the 2D character of the structure[6].
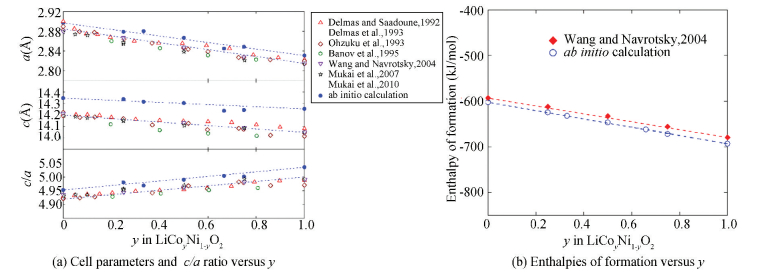
|
Figure 13 First-principles calculated data of LiCoyNi1-yO2[6](The dashed lines show linear trend of the data) |
The calculated enthalpies of formation for the O3-LiCoyNi1-yO2 (y = 0, 1/4, 1/3, 1/2, 2/3, 3/4 and 1) phases are shown in Fig. 13(b), which agree well with the experimental data[6]. Similar to the trend of the lattice parameters, both the theoretical and experimental results for the enthalpies of formation show an approximately linear correlation versus the Co content[6]. Thus, the solid solution of LiCoO2 and LiNiO2 has been considered to be an ideal solution[6]. The thermodynamic description of the Li-(Co, Ni)-O system has been obtained by extrapolation[6].
As the calculations of the cell voltages for Li/O3-LixCoO2 and Li/O3-LixNiO2 agree well with the experimental data, it is reliable to predict the cell voltages of Li/O3-LixCoyNi1-yO2 (0 ≤ x ≤ 1, 0 < y < 1). Four Li/O3-LixCoyNi1-yO2 cells (y = 0.3, 0.5, 0.6 and 0.8) have been presented as examples[6], the calculated cell voltages at 300 K are shown in Fig. 14. Because no experimental open circuit voltage is available, the first charge/discharge profiles during cycling of these cells are shown as a comparison. In all the cases, the calculations agree well with the experimental data[6], which shows a success of the thermodynamic description in predictions of cell voltages for Li ion batteries.

|
Figure 14 Cell voltages of Li/O3-LixCoyNi1-yO2 (0.4 ≤x≤ 1) at 300 K[6] |
4.4.5 The Li-Sb system
Considering all the experimental data, the Li-Sb phase diagram has been calculated using the CALPHAD approach[34] as shown in Fig. 15. Besides, the variation of electromotive force with temperature at various compositions and the coulometric titration curves of the Li-Sb system were calculated in Figs. 16 and 17, which show that the calculated results exhibit a good agreement with the experimental data. The thermodynamic description of the Li-Sb system[34] was reasonable and the thermodynamic parameters could be used for the establishment of the thermodynamic database for Li-Sb-based system.
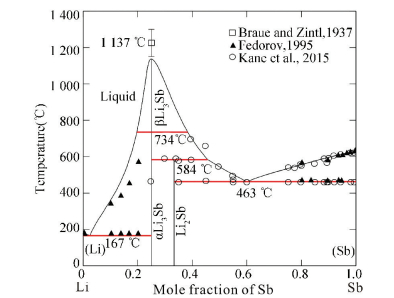
|
Figure 15 Calculated Li-Sb phase diagram[34] |

|
Figure 16 Calculated temperature variation of EMF at various compositions[34] |
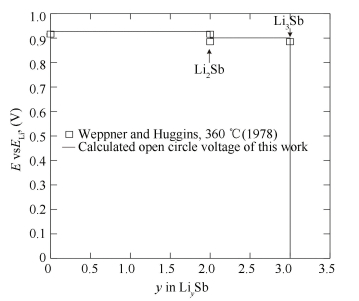
|
Figure 17 Calculated open circle voltage of Li-Sb alloy against pure Li at 633 K[34] |
4.4.6 The Li-Sn system
Based on DFT, the equilibrium open-circuit voltage[54] was calculated as shown in Fig. 18, which was consistent with the experimental determination[47-48]. Courtney et al.[55] calculated the theoretical electrochemical voltage profile of the Li-Sn system and found that the calculated results could well reproduce the experimental work for x > 2.5, but for x < 2.5 the equilibrium electrochemical voltage were not formed in the room-temperature electrochemical cell. Considering the elastic-stain energy contribution, the phase evolution of the Li-Sn battery was analyzed based on DFT [54], which indicated that the whole lithiated processes could be classified into the two-phase equilibrium process and the selective equilibrium. For the two-phase equilibrium process[54], thermodynamic driving force is large enough to facilitate the phase transition and the plateau voltage could be established. For the selective equilibrium[54], thermodynamic driving force is not enough to facilitate the nucleation of the new equilibrium phase due to the elastically constrained conditions and the plateau voltage unformed. Fig. 19 shows a schematic illustration of these two processes[54].The left part indicates the process of the two-phase equilibrium, which shows one plateau at its lithiated range; the right part indicates the selective equilibrium, which shows that the voltage decreases continuously at its lithiated range.
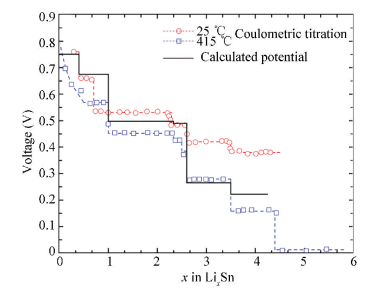
|
Figure 18 Calculated open-circuit voltage of the Li-Sn system[35] and compared with the Coulometric titration data at 415 ℃[52]and 25 ℃[54] |
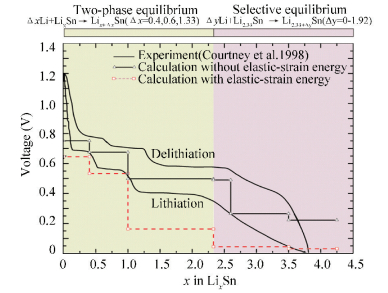
|
Figure 19 Schematic illustration showing the progress of lithiation of a Sn electrode[35] |
4.4.7 Other examples
The Li-Mn-Ni-O system has received much attention for potential positive electrode materials and the pseudo-ternary system Li2O2-Mn2O3-NiO has been studied with solution-based combinatorial samples of lithium manganese nickel oxide[120-122]. The areas of the Gibbs triangle that lie between the layered and spinel structures as well as the single-phase layered region has been reported[120]. The layered solid solution region has been determined and found to be made up of a single composition line joining LiCoO2 to Li2MnO3[121]. The solid solution undergoes a phase separation during slow cooling and the end points are the Co-rich phase containing some Mn and the Mn-rich phase containing some Co[121]. Also, metal site vacancies are present in the structures in increasing amounts as the lithium content of the samples decreases[122]. The relationship between the stoichiometry and stability of the electrode materials has been reported, which is crucial for material design.
5 ConclusionsAdvanced LIBs require lower cost, lower capacity loss, longer lifetime, higher energy density, higher stability and inherent safety. The Li-(Co, M)-O(M= transition metals) and Li-metal systems, as promising candidates for future electrodes in LIBs, are of great interest. The CALPHAD approach integrated with first-principles calculations and empirical methods has been applied to study the Li-(Co, Ni)-O, Li-Sb and Li-Sn systems as electrode materials in Li ion batteries. All the phases can be described with appropriate sublattice models and parameters. The calculations on their phase diagrams and thermodynamic properties are in good agreement with literature data. Using the derived thermodynamic description, the cell voltages have been well reproduced/predicted. This shows that CALPHAD has successfully been applied to study the phase equilibria, thermodynamic and electrochemical properties of electrode materials in LIBs. Furthermore, the thermodynamic datasets obtained for these systems enables the establishment of a whole thermodynamic database for multi-component Li-containing systems and the design of future electrode materials with improved stability and efficiency.
| [1] |
Nazri G A, Pistoia G. Lithium Batteries: Science and Technology. Boston: Kluwer Academic Publishers, 2003.
( 0) 0)
|
| [2] |
Tarascon J M, Armand M. Issues and challenges facing rechargeable lithium batteries. Nature, 2001, 414: 359-367. DOI:10.1038/35104644 ( 0) 0)
|
| [3] |
Armand M, Tarascon J-M. Building better batteries. Nature, 2008, 451: 652-657. DOI:10.1038/451652a ( 0) 0)
|
| [4] |
Hu L, Wu H, Mantia F L, et al. Thin, flexible secondary Li-Ion paper batteries. ACS Nano, 2010, 4(10): 5843-5848. DOI:10.1021/nn1018158 ( 0) 0)
|
| [5] |
Poizot P, Laruelle S, Grugeon S, et al. Nano-sized transition-metal oxides as negative-electrode materials for lithium-ion batteries. Nature, 2000, 407: 496-499. DOI:10.1038/35035045 ( 0) 0)
|
| [6] |
Chang K, Hallstedt B, Music D. Thermodynamic description of the LiNiO2-NiO2 pseudo-binary system and extrapolation to the Li(Co, Ni)O2-(Co, Ni)O2 system. Calphad, 2012, 37: 100-107. DOI:10.1016/j.calphad.2012.02.006 ( 0) 0)
|
| [7] |
Huggins R A. Advanced Batteries: Materials Science Aspects. New York: Springer, 2009.
( 0) 0)
|
| [8] |
Meng Y S, Arroyo-de Dompablo M E. First principles computational materials design for energy storage materials in lithium ion batteries. Energy Environ. Sci., 2009, 6(2): 589-609. DOI:10.1039/B901825E ( 0) 0)
|
| [9] |
Ceder C, Van der Ven A. Phase diagrams of lithium transition metal oxides: investigations from first principles. Electrochimica Acta, 1999, 45(1-2): 131-150. DOI:10.1016/S0013-4686(99)00199-1 ( 0) 0)
|
| [10] |
Wang L, Maxisch T, Ceder G. A first-principles approach to studying the thermal stability of oxide cathode materials. Chem. Mater., 2007, 19: 543-552. DOI:10.1021/cm0620943 ( 0) 0)
|
| [11] |
Ceder G, Chiang Y-M, Sadoway D R, et al. Identification of cathode materials for lithium batteries guided by first-principles calculations. Nature, 1998, 392: 694-696. DOI:10.1038/33647 ( 0) 0)
|
| [12] |
Ceder G. Predicting properties from scratch. Science, 1998, 280(5366): 1099-1100. DOI:10.1126/science.280.5366.1099 ( 0) 0)
|
| [13] |
Kang K, Meng Y S, Bréger J, et al. Electrodes with high power and high capacity for rechargeable lithium batteries. Science, 2006, 311(5763): 977-980. DOI:10.1126/science.1122152 ( 0) 0)
|
| [14] |
Chang K, Hallstedt B, Music D. Thermodynamic and electrochemical properties of the Li-Co-O and Li-Ni-O systems. Chemistry of Materials, 2012, 24(1): 97-105. DOI:10.1021/cm201964r ( 0) 0)
|
| [15] |
Delmas C, Fouassier C, Hagenmuller P. Structural classification and properties of the layered oxides. Physica B+C, 1980, 99(1-4): 81-85. DOI:10.1016/0378-4363(80)90214-4 ( 0) 0)
|
| [16] |
Berthelot R, Carlier D, Pollet M, et al. Synthesis and investigations on an O4-LiCoO2 polytype. Electrochem. Solid-State Lett., 2009, 12(11): A207-A210. DOI:10.1149/1.3204643 ( 0) 0)
|
| [17] |
Komaba S, Yabuuchi N, Kawamoto Y. A new polymorph of layered LiCoO2. Chem. Lett., 2009, 38(10): 954-955. DOI:10.1246/cl.2009.954 ( 0) 0)
|
| [18] |
Ohzuku T, Ueda A. Why transition metal (di) oxides are the most attractive materials for batteries. Solid State Ionics, 1994, 69(3-4): 201-211. DOI:10.1016/0167-2738(94)90410-3 ( 0) 0)
|
| [19] |
Masataka W. Recent developments in lithium ion batteries. Materials Science and Engineering: R: Reports, 2001, 33(4): 109-134. DOI:10.1016/S0927-796X(01)00030-4 ( 0) 0)
|
| [20] |
Ohzuku T, Ueda A, Nagayama M. Electrochemistry and structural chemistry of LiNiO2 (R 3 m) for 4 volt secondary lithium cells. J. Electrochem. Soc., 1993, 140(7): 1862-1870. DOI:10.1149/1.2220730 ( 0) 0)
|
| [21] |
Arai H, Okada S, Ohtsuka H, et al. Characterization and cathode performance of Li1-xNi1+xO2 prepared with the excess lithium method. Solid State Ionics, 1995, 80(3-4): 261-269. DOI:10.1016/0167-2738(95)00144-U ( 0) 0)
|
| [22] |
Castro-García S, Julien C, Señarís-Rodríguez M A. Structural and electrochemical properties of Li-Ni-Co oxides synthesized by wet chemistry via a succinic-acid-assisted technique. Int. J. Inorg. Mater., 2001, 3: 323-329. DOI:10.1016/S1466-6049(01)00040-X ( 0) 0)
|
| [23] |
Wang M, Navrotsky A. Enthalpy of formation of LiNiO2, LiCoO2 and their solid solution, LiNi1-xCoxO2. Solid State Ionics, 2004, 166(1-2): 167-173. DOI:10.1016/j.ssi.2003.11.004 ( 0) 0)
|
| [24] |
Delmas C, Saadoune I. Electrochemical and physical properties of the LixNi1-yCoyO2 phases. Solid State Ionics, 1992, 53(Part 1): 370-375. DOI:10.1016/0167-2738(92)90402-B ( 0) 0)
|
| [25] |
Abdel Ghany A E, Hashem A M A, Abuzeid H A M. Synthesis, structure characterization and magnetic properties of nanosize LiCo1-yNiyO2 prepared by sol-gel citric acid route. Ionics, 2009, 15(1): 49-59. DOI:10.1007/s11581-008-0273-5 ( 0) 0)
|
| [26] |
Cabana J, Monconduit L, Larcher D, et al. Beyond intercalation-based Li-ion batteries: the state of the art and challenges of electrode materials reacting through conversion reactions. Adv. Mater., 2010, 22(35): E170-E192. DOI:10.1002/adma.201000717 ( 0) 0)
|
| [27] |
Gao Q, Wang J, Shang S, et al. First-principles calculations of finite-temperature thermodynamic properties of binary solid solutions in the AlCuMg system. Calphad, 2014, 47: 196-210. DOI:10.1016/j.calphad.2014.10.004 ( 0) 0)
|
| [28] |
Chang K, Music D, Baben M T, et al. Modeling of metastable phase formation diagrams for sputtered thin films. Sci. Technol. Adv. Mater., 2016, 17(1): 210-219. DOI:10.1080/14686996.2016.1167572 ( 0) 0)
|
| [29] |
Chang K, to Baben M, Music D, et al. Estimation of the activation energy for surface diffusion during metastable phase formation. Acta Mater., 2015, 98: 135-140. DOI:10.1016/j.actamat.2015.07.029 ( 0) 0)
|
| [30] |
Abe T, Koyama T. Thermodynamic modeling of the LiCoO2-CoO2 pseudo-binary system. CALPHAD:Computer Coupling of Phase Diagrams and Thermochemistry, 2011, 35: 209-218. DOI:10.1016/j.calphad.2011.02.006 ( 0) 0)
|
| [31] |
Chang K, Hallstedt B, Music D, et al. Thermodynamic description of the layered O3 and O2 structural LiCoO2-CoO2 pseudo-binary systems. Calphad, 2013, 41: 6-15. DOI:10.1016/j.calphad.2013.01.001 ( 0) 0)
|
| [32] |
Lepple M, Adam R, Cupid D M, et al. Thermodynamic investigations of copper oxides used as conversion type electrodes in lithium ion batteries. J. Mater. Sci., 2013, 48: 5818-5826. DOI:10.1007/s10853-013-7374-x ( 0) 0)
|
| [33] |
Chang K, Music D, Strafela M, et al. Quantum mechanically guided design of amorphous Si-Al-M (M = 3d metals) anodes for Li ion batteries. Solid State Ionics, 2017, 303: 47-51. DOI:10.1016/j.ssi.2017.02.011 ( 0) 0)
|
| [34] |
Zhang Fan, Liu Shuhong, Wang Jianchuan, et al. Experimental investigation and thermodynamic assessment of the Li-Sb system. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry, 2017, 57: 28-36. DOI:10.1016/j.calphad.2017.01.005 ( 0) 0)
|
| [35] |
Zhang F, Wang J, Liu S, et al. Effects of the volume changes and elastic-strain energies on the phase transition in the Li-Sn battery. Journal of Power Sources, 2016, 330: 111-119. DOI:10.1016/j.jpowsour.2016.08.136 ( 0) 0)
|
| [36] |
Sangster J, Pelton A D. The Li-Sb (Lithum-Antimony) system. J. Phase Equilib., 1993, 14(4): 514-517. DOI:10.1007/BF02671973 ( 0) 0)
|
| [37] |
Brauer G, Zintl E. Konstitution von phosphiden, arseniden, antimoniden, und wismutiden des lithiums, natriums und kaliums. Z. Phys. Chem., 1937, B37(5-6): 323-352. ( 0) 0)
|
| [38] |
Weppner W, Huggins R A. Thermodynamic properties of the intermetallic systems lithium-antimony and lithium-bismuth. J. Electrochem. Soc., 1978, 125(1): 7-14. DOI:10.1149/1.2131401 ( 0) 0)
|
| [39] |
Lebeau E, Hebd C R. On the action of Li on Sb in liquid ammonia and the properties of Li3Sb. Séances Acad. Sci., 1902, 134: 284-286. ( 0) 0)
|
| [40] |
Fedorov P I. Lithium-antimony system. Russ. J. Inorg. Chem., 1995, 40(5): 815-817. ( 0) 0)
|
| [41] |
Kane M M, Newhouse J M, Sadoway D R. Electrochemical determination of the thermodynamic properties of lithium-antimony alloys. J. Electrochem. Soc., 2015, 162(3): A421-A425. DOI:10.1149/2.0671503jes ( 0) 0)
|
| [42] |
Weppner W, Huggins R A. Thermodynamic properties of the intermetallic systems lithium-antimony and lithium-bismuth. J. Electrochem. Soc., 1978, 125(1): 7-14. DOI:10.1149/1.2131401 ( 0) 0)
|
| [43] |
Shchukarev S A, Vol'f E, Morozova M E, et al. Khim, 1954, 24: 1925-1926. DOI:10.1149/1.2131401 ( 0) 0)
|
| [44] |
Kubaschewski O, Catterall J A. Catterall: Thermochemical Data of Alloys(Metal Physics and Physical Metallurgy, Vol. 3). London: Pergamon Press, 1956.
( 0) 0)
|
| [45] |
Nikitin A V, Demidov A I, Morachevskii A G, et al. Thermodynamics of solid alloys in the Li-Sb system. Zh. Prikl. Khim., 1972, 55(4): 915-916. ( 0) 0)
|
| [46] |
Terlicka S, Debski A, Fima P. Enthalpy of formation of Li2Sb and Li3Sb and mixing enthalpy of liquid Li-Sb alloys. Journal of Alloys and Compounds, 2016, 673: 272-277. DOI:10.1016/j.jallcom.2016.02.235 ( 0) 0)
|
| [47] |
Wen C J, Huggins R A. Thermodynamic study of the lithium-tin system. J. Electrochem. Soc., 1981, 128: 1181-1187. DOI:10.1149/1.2127590 ( 0) 0)
|
| [48] |
Wang J, Raistrick I D, Huggins R A. Behavior of some binary lithium alloys as negative electrodes in organic solvent-based electrolytes. J. Electrochem. Soc., 1986, 133: 487-460. DOI:10.1149/1.2108601 ( 0) 0)
|
| [49] |
Sangster J, Bale C W. The Li-Sn (Lithium-Tin) system. Journal of Phase Equilibria, 1998, 19(1): 70-75. DOI:10.1361/105497198770342788 ( 0) 0)
|
| [50] |
Li D, Fürtauer S, Flandorfer H, et al. Thermodynamic assessment and experimental investigation of the Li-Sn system. Calphad, 2014, 47: 181-195. DOI:10.1016/j.calphad.2014.09.002 ( 0) 0)
|
| [51] |
Courtney I A, Dahn J R. Electrochemical and in Situ X-Ray diffraction studies of the reaction of lithium with tin oxide composites. J. Electrochem. Soc., 1997, 144(6): 2045-2052. DOI:10.1149/1.1837740 ( 0) 0)
|
| [52] |
Beaulieu L Y, Beattie S D, Hatchard T D, et al. The electrochemical reaction of lithium with tin studied by in situ AFM. J. Electrochem. Soc., 2003, 150(4): A419-A424. DOI:10.1149/1.1556595 ( 0) 0)
|
| [53] |
Rhodes K J, Meisner R, Kirkham M, et al. In situ XRD of thin film tin electrodes for lithium ion batteries. Journal of the Electrochemical Society, 2012, 159(3): A294-A299. DOI:10.1149/2.077203jes ( 0) 0)
|
| [54] |
Chao S C, Song Y F, Wang C C, et al. Study on microstructural deformation of working Sn and SnSb Anode Particles for Li-Ion batteries by in situ transmission X-ray microscopy. Journal of Physical Chemistry C, 2011, 115: 22040-22047. DOI:10.1021/jp206829q ( 0) 0)
|
| [55] |
Courtney I A, Tse J S, Mao O, et al. Ab-initio calculations of the lithium-tin voltage profile. Phys. Rev. B, 1998, 58: 15583-15588. DOI:10.1103/PhysRevB.58.15583 ( 0) 0)
|
| [56] |
Hillert M. A discussion of methods of calculating phase diagrams. Bull. Alloy Phase Diagrams, 1981, 2: 265-268. DOI:10.1007/BF02868269 ( 0) 0)
|
| [57] |
Seifert H J, Aldinger F. Applied phase studies. Z. Metallkd., 1996, 87(11): 841-853. ( 0) 0)
|
| [58] |
Andersson J-O, Helander T, Höglund L, et al. Thermo-Calc & DICTRA, computational tools for materials science. Calphad, 2002, 26(2): 273-312. DOI:10.1016/S0364-5916(02)00037-8 ( 0) 0)
|
| [59] |
Hillert M. The compound energy formalism. Journal of Alloys and Compounds, 2001, 320(2): 161-176. DOI:10.1016/S0925-8388(00)01481-X ( 0) 0)
|
| [60] |
Ansara I, Dupin N, Lukas H L, et al. Thermodynamic assessment of the Al-Ni system. J. Alloys Compd., 1997, 247(1-2): 20-30. DOI:10.1016/S0925-8388(96)02652-7 ( 0) 0)
|
| [61] |
Chang K, Hallstedt B. Thermodynamic assessment of the Li-O system. CALPHAD: Computer Coupling of Phase Diagrams and Thermochemistry, 2011, 35: 160-164. DOI:10.1016/j.calphad.2011.02.003 ( 0) 0)
|
| [62] |
Chen Z, Dahn J R. Methods to obtain excellent capacity retention in LiCoO2 cycled to 4.5 V. Electrochimica Acta, 2004, 49(7): 1079-1090. DOI:10.1016/j.electacta.2003.10.019 ( 0) 0)
|
| [63] |
Wolverton C, Zunger A. First-principles prediction of vacancy order-disorder and intercalation battery voltages in LixCoO2. Physical Review Letters, 1998, 81(3): 606-609. DOI:10.1103/PhysRevLett.81.606 ( 0) 0)
|
| [64] |
Sholl D, Steckel J A. Density Functional Theory: A Practical Introduction. Hoboken: John Wiley and Sons, 2009.
( 0) 0)
|
| [65] |
Wolverton C, Yan X-Y, Vijayaraghavan R, et al. Incorporating first-principles energetics in computational thermodynamics approaches. Acta Materialia, 2002, 50(9): 2187-2197. DOI:10.1016/S1359-6454(01)00430-X ( 0) 0)
|
| [66] |
Zhong Y, Wolverton C, Chang Y A, et al. A combined CALPHAD/first-principles remodeling of the thermodynamics of Al-Sr: Unsuspected ground state energies by "rounding up the (un)usual suspects". Acta Mater., 2004, 52: 2739-2754. DOI:10.1016/j.actamat.2004.02.022 ( 0) 0)
|
| [67] |
Zhang L, Wang J, Du Y, et al. Thermodynamic properties of the Al-Fe-Ni system acquired via a hybrid approach combining calorimetry, first principles and CALPHAD. Acta Mater., 2009, 18: 5324-5341. DOI:10.1016/j.actamat.2009.07.031 ( 0) 0)
|
| [68] |
Djurovic D, Hallstedt B, von Appen J, et al. Thermodynamic assessment of the Mn-C system. CALPHAD, 2010, 34(3): 279-285. DOI:10.1016/j.calphad.2010.05.002 ( 0) 0)
|
| [69] |
Hallstedt B, Music D, Sun Z. Thermodynamic evaluation of the Al-Cr-C system. Int. J. Mat. Res., 2006, 97(5): 539-542. DOI:10.3139/146.101270 ( 0) 0)
|
| [70] |
Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B, 1996, 54: 11169-11186. DOI:10.1103/PhysRevB.54.11169 ( 0) 0)
|
| [71] |
Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B, 1999, 59(3): 1758-1775. DOI:10.1103/PhysRevB.59.1758 ( 0) 0)
|
| [72] |
Kubaschewski O, Alcock C B, Spencer P J. Materials Thermochemistry. New York: Pergamon Press, 1993.
( 0) 0)
|
| [73] |
Knapp W J, van Vorst W D. Some semiempirical methods for estimating the entropies of oxides, silicates, and the prediction of reaction equilibria and yields. Journal of American Ceramic Society, 1951, 34(12): 384-387. DOI:10.1111/j.1151-2916.1951.tb13019.x ( 0) 0)
|
| [74] |
Huang G S, Xu Z H. Thermochemistry of inorganic compounds: Part 1. estimation of entropies of AxBy types of solids. Thermochim. Acta, 1988, 136(1): 133-137. DOI:10.1016/0040-6031(88)87433-1 ( 0) 0)
|
| [75] |
Peng S, Grimvall G. A method to estimate entropies and heat capacities applied to alkali oxides. International Journal of Thermophysics, 1994, 15(5): 973-981. DOI:10.1007/BF01447107 ( 0) 0)
|
| [76] |
Sangster J, Pelton A D. The Li-O (Lithium-Oxygen) system. J. Phase Equilib., 1992, 13(3): 296-299. DOI:10.1007/BF02667558 ( 0) 0)
|
| [77] |
Hoffman E E. The solubility of O and N in Li and methods of Li purification. U.S. Atomic Energy Commission Report ORNL-2894, 1960. ( 0) 0)
|
| [78] |
Konovalov E E, Seliverstov N I, Emelyanov V P. Solubility of oxygen and chlorine in liquid lithium. Russ. Metal., 1968, 3: 77-78. ( 0) 0)
|
| [79] |
Cheburkov V I, Rozanov A N. Reaction kinetics of molten Li with O and N. Metalloved. Chist. Metal., 1968, 7: 168-173. ( 0) 0)
|
| [80] |
Yonco R M, Moroni V A, Strain J E, et al. A determination of the solubility of Li2O in liquid Li by fast neutron activation. J. Nucl. Mater., 1979, 79(2): 354-362. DOI:10.1016/0022-3115(79)90100-4 ( 0) 0)
|
| [81] |
Jaeger F M, van Klooster H S. Proc. R. Acad. Amsterdam., 1914, 16: 857-880. ( 0) 0)
|
| [82] |
van Arkel A E, Flood E A, Bright N F H. The electrical conductivity of molten Oxides. Can. J. Chem., 1953, 31(11): 1009-1019. DOI:10.1139/v53-133 ( 0) 0)
|
| [83] |
Knacke O, Kubaschewski O, Hesselmann K. Thermochemical Properties of Inorganic Substances. Berlin: Springer, 1991.
( 0) 0)
|
| [84] |
Brewer L, Margrave J. The vapor pressures of lithium and sodium oxides. Journal of Physical Chemistry, 1955, 59: 421-425. DOI:10.1021/j150527a010 ( 0) 0)
|
| [85] |
Papin G, Michaud M, Bouaziz R. Lithium carbonate-lithium oxide binary system. C.R. Acad. Sci., Paris, Ser. C, 1969, 268(19): 1691-1693. ( 0) 0)
|
| [86] |
Akiyama M, Ando K, Oishi Y. Synthesis of Li2O single crystal by vacuum fusion technique. Journal of Nuclear Science and Technology, 1980, 17(2): 154-155. DOI:10.1080/18811248.1980.9732558 ( 0) 0)
|
| [87] |
Ortman M S, Larsen E M. Preparation, characterization, and melting point of high-purity lithium oxide. J.Am. Ceram. Soc., 1983, 66(9): 645-648. DOI:10.1111/j.1151-2916.1983.tb10614.x ( 0) 0)
|
| [88] |
Brewer L. Thermodynamic properties of the oxides and their vaporization processes. Chem. Rev., 1953, 52(1): 1-75. DOI:10.1021/cr60161a001 ( 0) 0)
|
| [89] |
Tzentnershver M, Blumenthal M. Bull. Intern. Acad. Polonaise. Classe Sci. Math. Nat. A, 1933, 499-522. ( 0) 0)
|
| [90] |
Rode T V, Dobrynina T A, Golder G A. Physicochemical study of lithium peroxide. Bulletin of the Academy of Sciences of the USSR, Division of Chemical Science, 1955, 4(4): 545-553. DOI:10.1007/BF01167333 ( 0) 0)
|
| [91] |
Notz K J, Bach R O. Chimia, 1963, 17: 158-159. ( 0) 0)
|
| [92] |
Tsentsiper A B, Kuznetsova Z I. Bull. Acad. Sci. USSR, Div. Chem. Sci., 1965, 14: 1873-1875. DOI:10.1007/BF00850186 ( 0) 0)
|
| [93] |
Ferapontov Y A, Kokoreva N V, Kozlova N P, et al. Thermal analysis of lithium peroxide prepared by various methods. Russian Journal of General Chemistry, 2009, 79(5): 891-894. DOI:10.1134/S1070363209050041 ( 0) 0)
|
| [94] |
Kolesov V P, Skuratov S M, Zaikin I D. Russ. J. Inorg. Chem, 1959, 4: 558-560. ( 0) 0)
|
| [95] |
Johnson G K, Grow R T, Hubbard W N. The enthalpy of formation of lithium oxide (Li2O). The Journal of Chemical Thermodynamics, 1975, 7(8): 781-786. DOI:10.1016/0021-9614(75)90254-2 ( 0) 0)
|
| [96] |
de Forcrand H R. Ann. Chim. Phys., 1908, 15: 433-490. ( 0) 0)
|
| [97] |
Johnston H L, Bauer T W. Low temperature heat capacities of inorganic solids. Ⅶ. Heat capacity and thermodynamic functions of Li2O. Thermodynamics of the Li2O-H2O system1. J. Am. Chem. Soc., 1951, 73(3): 1119-1122. DOI:10.1021/ja01147a070 ( 0) 0)
|
| [98] |
Glassner A, The thermochemical properties of the oxides, fluorides, and chlorides to 2 500°K. Illinois: Argonne National Laboratory, ANL-5750, 1957.
https://www.researchgate.net/publication/242919905_The_Thermochemical_Properties_of_the_Oxides_Fluorides_and_Chlorides_to_2500_deg_K
( 0) 0)
|
| [99] |
Shomate C H, Cohen A J. High-temperature heat content and entropy of lithium oxide and lithium hydroxide. Journal of the American Chemical Society, 1955, 77: 285-286. DOI:10.1021/ja01607a010 ( 0) 0)
|
| [100] |
Rodigina E N, Gomelskii K Z. Russ. J. Phys. Chem., 1961, 35: 898-901. ( 0) 0)
|
| [101] |
Tanifuji T, Shiozawa K, Nasu S. Heat capacity of lithium oxide from 306 to 1073 K. Journal of Nuclear Materials, 1978, 78(2): 422-424. DOI:10.1016/0022-3115(78)90464-6 ( 0) 0)
|
| [102] |
de Forcrand H R, Hebd C R. Séances Acad. Sci., 1900, 130: 1465-1468. ( 0) 0)
|
| [103] |
Tanifuji T, Nasu S. Heat capacity and thermal decomposition of lithium peroxide. Journal of Nuclear Materials, 1979, 87(1): 189-195. DOI:10.1016/0022-3115(79)90138-7 ( 0) 0)
|
| [104] |
Ménétrier M, Saadoune I, Levasseur S, et al. The insulator-metal transition upon lithium deintercalation from LiCoO2: electronic properties and 7Li NMR study. J. Mater. Chem., 1999, 9: 1135-1140. DOI:10.1039/A900016J ( 0) 0)
|
| [105] |
Levasseur S, Ménétrier M, Suard E, et al. Evidence for structural defects in non-stoichiometric HT-LiCoO2: electrochemical, electronic properties and 7Li NMR studies. Solid State Ionics, 2000, 128(1-4): 11-24. DOI:10.1016/S0167-2738(99)00335-5 ( 0) 0)
|
| [106] |
Kellerman D G, Galakhov V R, Semenova A S, et al. Semiconductor-metal transition in defect lithium cobaltite. Physics of the Solid State, 2006, 48(3): 548-556. DOI:10.1134/S106378340603022X ( 0) 0)
|
| [107] |
Ito A, Tanaka K, Kawaji H, et al. Magnetic phase transition of Li0.75CoO2 compared with LiCoO2 and Li0.5CoO2. Journal of Thermal Analysis and Calorimetry, 2008, 92: 399-401. DOI:10.1007/s10973-007-8959-x ( 0) 0)
|
| [108] |
Marianetti C A, Kotliar G, Ceder G. A first-order Mott transition in LixCoO2. Nature Materials, 2004, 3: 627-631. DOI:10.1038/nmat1178 ( 0) 0)
|
| [109] |
Croguennec L, Suard E, Willmann P, et al. Structural and electrochemical characterization of the LiNi1-yTiyO2 electrode materials obtained by direct solid-state reactions. Chem. Mater., 2002, 14(5): 2149-2157. DOI:10.1021/cm011265v ( 0) 0)
|
| [110] |
Shinova E, Zhecheva E, Stoyanova R, et al. High-pressure synthesis of solid solutions between trigonal LiNiO2 and monoclinic Li[Li1/3Ni2/3]O2. Journal of Solid State Chemistry, 2005, 178(5): 1661-1669. DOI:10.1016/j.jssc.2005.03.007 ( 0) 0)
|
| [111] |
Antaya M, Cearns K, Preston J S, et al. In situ growth of layered, spinel, and rock-salt LiCoO2 by laser ablation deposition. Journal of Applied Physics, 1994, 76(5): 2799-2806. DOI:10.1063/1.357514 ( 0) 0)
|
| [112] |
Kanno R, Kubo H, Kawamoto Y, et al. Phase relationship and lithium deintercalation in lithium nickel oxides. Journal of Solid State Chemistry, 1994, 110(2): 216-225. DOI:10.1006/jssc.1994.1162 ( 0) 0)
|
| [113] |
Guilmard M, Croguennec L, Denux D, et al. Thermal stability of lithium nickel oxide derivatives. Part I: LixNi1.02O2 and LixNi0.89Al0.16O2 (x = 0.50 and 0.30). Chem. Mater., 2003, 15(23): 4476-4483. DOI:10.1021/cm030059f ( 0) 0)
|
| [114] |
Chazel C, Ménétrier M, Carlier D, et al. DFT modeling of NMR contact shift mechanism in the ideal LiNi2O4 spinel and application to thermally treated layered Li0.5NiO2. Chem. Mater., 2007, 19(17): 4166-4173. DOI:10.1021/cm070324n ( 0) 0)
|
| [115] |
Delmas C, Saadoune I, Rougier A. The cycling properties of the LixNi1-yCoyO2 electrode. Journal of Power Sources, 1993, 44(1-3): 595-602. DOI:10.1016/0378-7753(93)80208-7 ( 0) 0)
|
| [116] |
Ohzuku T, Ueda A, Nagayama M, et al. Comparative study of LiCoO2, LiNi12Co12O2 and LiNiO2 for 4 volt secondary lithium cells. Electrochimica Acta, 1993, 38(9): 1159-1167. DOI:10.1016/0013-4686(93)80046-3 ( 0) 0)
|
| [117] |
Banov B, Bourilkov J, Mladenov M. Cobalt stabilized layered lithium-nickel oxides, cathodes in lithium rechargeable cells. Journal of Power Sources, 1995, 54(2): 268-270. DOI:10.1016/0378-7753(94)02082-E ( 0) 0)
|
| [118] |
Mukai K, Sugiyama J, Ikedo Y, et al. Microscopic magnetism in lithium insertion materials of LiNi1-xCoxO2 (x = 0, 1/4, 1/2, 3/4, and 1). Journal of Power Sources, 2007, 174(2): 843-846. DOI:10.1016/j.jpowsour.2007.06.105 ( 0) 0)
|
| [119] |
Mukai K, Sugiyama J, Aoki Y. Structural, magnetic, and electrochemical studies on lithium insertion materials LiNi1-xCoxO2 with 0≤x≤0.25. Journal of Solid State Chemistry, 2010, 183(7): 1726-1732. DOI:10.1016/j.jssc.2010.05.019 ( 0) 0)
|
| [120] |
McCalla E, Rowe A W, Shunmugasundaram R, et al. Structural study of the Li-Mn-Ni oxide pseudoternary system of interest for positive electrodes of Li-Ion batteries. Chemistry of Materials, 2013, 25(6): 989-999. DOI:10.1021/cm4001619 ( 0) 0)
|
| [121] |
McCalla E, Lowartz C M, Brown C R, et al. Formation of layered-layered composites in the Li-Co-Mn oxide pseudoternary system during slow cooling. Chem. Mater., 2013, 25(6): 912-918. DOI:10.1021/cm304002b ( 0) 0)
|
| [122] |
McCalla E, Rowe A W, Camardese J, et al. The role of metal site vacancies in promoting Li-Mn-Ni-O layered solid solutions. Chemistry of Materials, 2013, 25(13): 2716-2721. DOI:10.1021/cm401461m ( 0) 0)
|
 2018, Vol. 25
2018, Vol. 25